矩阵变换器输出电流比例谐振控制研究*

孙宏光 夏益辉

(1.海军驻大连地区军事代表室 大连 116021)(2.海军工程大学电气工程学院 武汉 430033)

矩阵变换器输出电流比例谐振控制研究*

孙宏光1夏益辉2

(1.海军驻大连地区军事代表室 大连 116021)(2.海军工程大学电气工程学院 武汉 430033)

与传统的PI控制相比，比例谐振控制无需进行繁琐的坐标变换，不存在受电路参数影响的前馈补偿和耦合项，能够实现对正弦指令信号无静差跟踪，广泛用于交-直-交变频器中。在分析了矩阵变换器输出电路数学模型的基础上，提出了基于比例谐振输出电流闭环控制策略。对比例谐振控制器各参数对输出电流控制性能进行了研究，并在此基础上对一具体工况的参数进行了设计。通过将比例谐振控制用于矩阵变换器输出电流闭环控制进行仿真研究与实验验证，仿真与实验结果证明了所提控制方法是正确可行的。

比例谐振; 电流闭环; 矩阵变换器; 比例积分

1 引言

矩阵变换器作为一种变频驱动装置，它的主要应用对象是电机，对调速性能要求不高的场合可采用传统的开环控制即可满足要求，但对调速性能要求比较高的场合，必须得采用电机的闭环控制如矢量控制、直接转矩控制等[1～4]。电流环作为电机矢量控制的一个内环，其重要性对于电机调速性能的重要性不言而喻。

目前，矩阵变换器中对于输出电流闭环控制主要为滞环控制、预测控制和PI控制等[5～10]。滞环控制原理简单，易于实现，但其存在开关频率不恒定的缺点[5～6]；预测控制能够消除输入输出侧扰动对输出电流的影响，但其计算复杂[7～8]；PI控制由于其对直流信号具有无静差跟踪的特点[9～10]，广泛地应用于电机矢量控制和有源滤波器谐波补偿中，但其对交流信号无法实现无静差跟踪的目标，因此，必须对电流信号进行旋转变换，将给定参考信号变换为直流量，增加了系统的计算量。近年来，有学者提出了针对正弦信号的PR控制器[11～13]，可以避免旋转坐标变换，降低了计算量，可以获得与PI控制在旋转坐标系相同的跟踪性能，即能够快速无静差地跟踪正弦指令。

本文首先建立了矩阵变换器输出电流闭环控制的数学模型，并介绍了采用空间矢量调制方法实现输出电流闭环控制流程；其次，分析了PR控制器各参数对PR控制器和输出电流闭环控制系统的影响，并以此为基础对一具体工况的参数进行了选取；最后，对基于PR控制的输出电流闭环控制的性能进行了仿真研究与试验验证，仿真与试验结果表明将PR控制应用于矩阵变换器输出电流闭环控制是切实可行的。

2 矩阵变换器输出电流闭环控制数 学模型及空间矢量调制实现

2.1 输出电流闭环控制数学模型

图1为三相-三相矩阵变换器电路，该图中忽略了电源内部阻抗的影响。

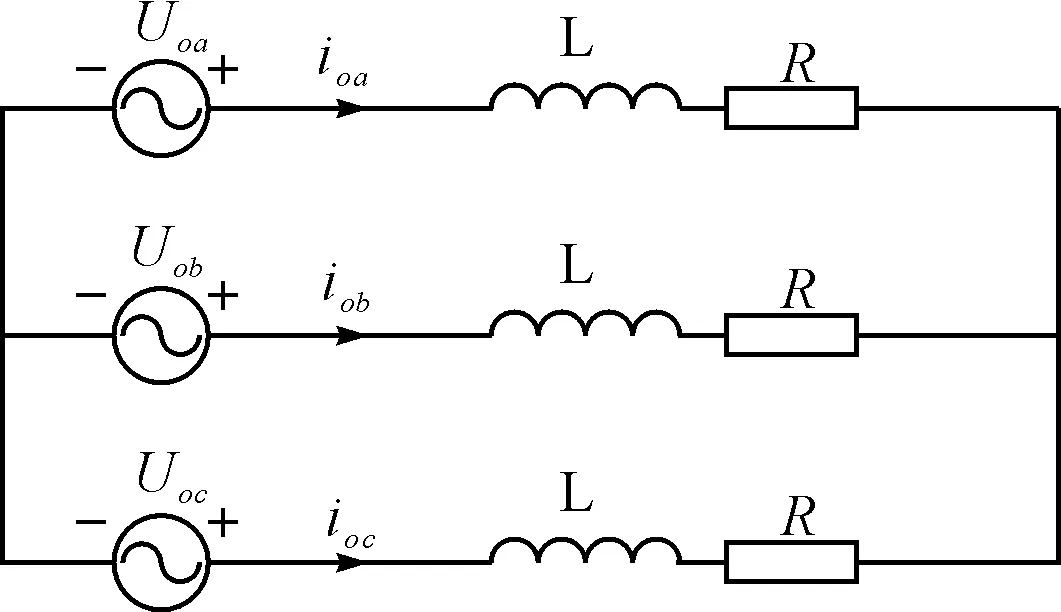
图1 矩阵变换器三相输出电路图

由图1可以得到：

(1)

将上式由三相静止变换为两相静止坐标后得：

(2)

由上式可得电流闭环控制框图如图2，由于α、β轴相同，这里只对α轴分析。

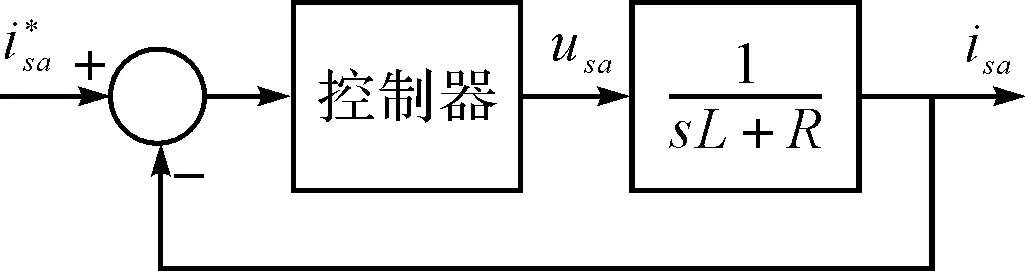
图2 α轴电流闭环控制框图

由式(2)可得空间矢量调制所需输出电压幅值uom和相位θv：

(3)

2.2 输出电流闭环控制的空间矢量实现

图3为基于输出电流闭环控制的矩阵变换器空间矢量实现框图。由图可知，通过对输出电流采用闭环控制，得到参考输出电压信号，该信号与网侧电压信息一起送入数字处理系统，在数字处理系统中利用空间矢量调制方法时时计算各开关管的占空比来合成期望的输出电压，进而获得期望的输出电流，达到输出电流跟踪指令电流的目的。

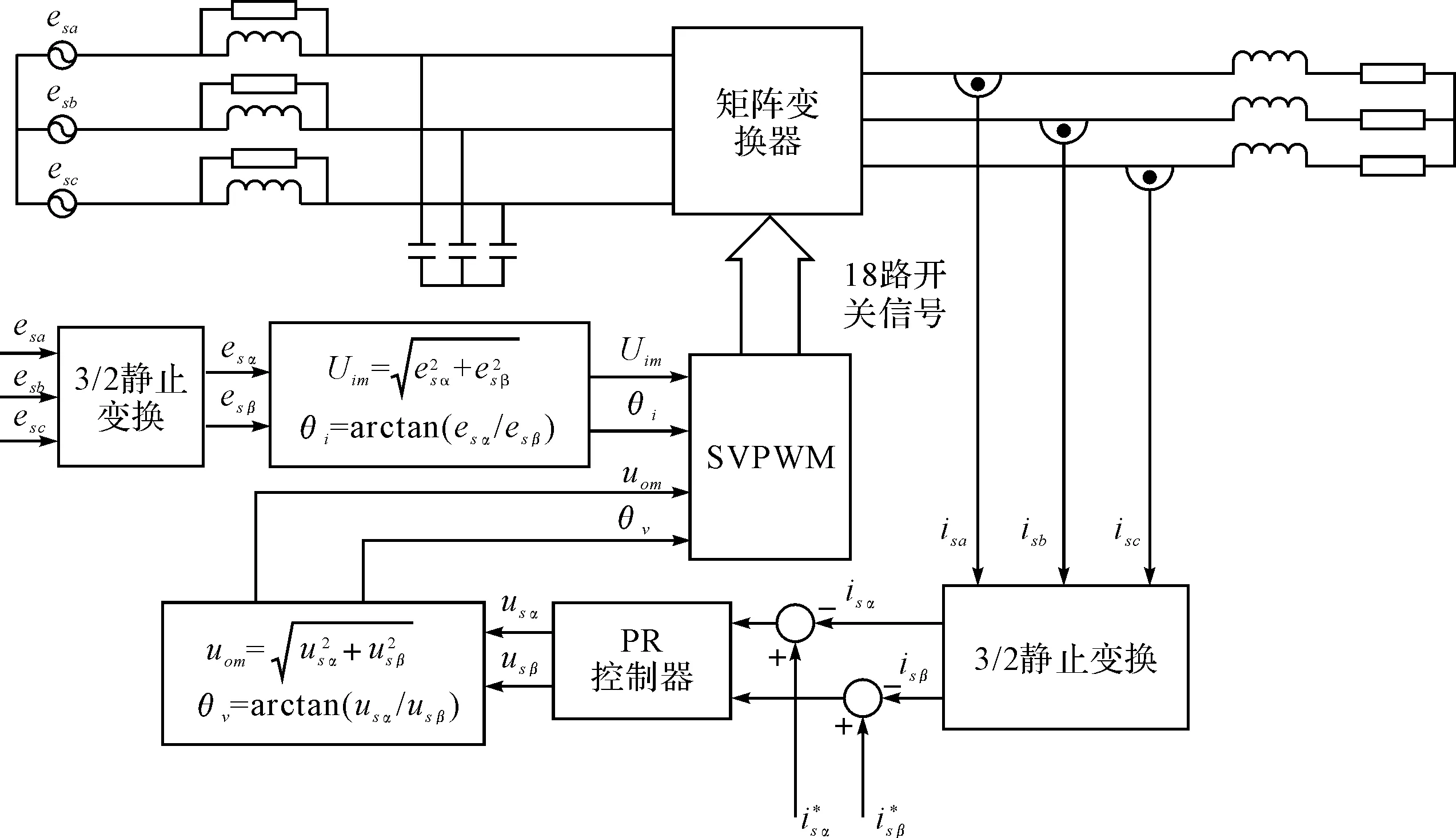
图3 输出电流闭环控制空间矢量实现框图

3 输出电流准PR控制器设计

PR控制器是根据三相系统中在旋转坐标系PI控制器能够无静差跟踪直流量的原理推到而得到的，PI控制可以看成是PR控制的一个特例(即输入信号为直流量，谐振频率为0)。

3.1 理想PR控制器

理想PR控制器的传递函数为

(4)

式中：kp为比例系数，影响系统对输入信号指令的动态响应速度；ki为谐振积分系数，决定系统对正弦输入信号的响应速度和跟踪精度。对于理想PR控制器，在谐振频率处，系统具有无穷大的增益，输出可以无静差的跟踪输入指令，但在谐振频率点附近，系统增益快速下降，当输入指令频率发生扰动时，输出并不能无静差跟踪输入指令，当前实际应用中的比例谐振控制均是引入一定带宽的。

3.2 实际应用的PR控制器

针对理想PR控制器存在的缺点，通过增加其截止频率来提高抗扰动能力，改进后的PR控制器传递函数为

(5)

式中kp、ki同理想PR控制器，ωc为谐振控制器的截止角频率。

3.3 输出电流闭环传递函数

将矩阵变换器看作一低通滤波器，图4为α轴电流闭环控制框图。

图4 α轴电流PR闭环控制框图

其中，Ts为开关周期，L、R分别为负载电感和电阻，由图4可得输出电流开环传递函数G1(s)。

(6)

由式(6)中存在两个小惯性环节，将其进行近似处理后可得：

(7)

将Ts=0.0002s，L=8mH，R=8Ω代入上式后得：

(8)

由式(9)可得系统的闭环传递函数φ1(s)：

(9)

3.4 PR控制器各参数对输出电流性能影响极其设计

由式(9)可知，系统输出电流跟踪输入电流的性能由参数kp、ki和ωc共同作用，由于电机额定工作频率通常为50Hz，所以这里取ωo=100π，当kp=40，ki=200，ωc=10π时，就各参数对输出电流性能影响的规律进行分析。

由图5(a)可知，随着kp的增加，谐振频率处幅值幅度变化不大，而输出频率低于谐振频率幅值幅度逐渐增大，说明增大kp，对谐振频率处作用不大，而对输出频率小于谐振频率影响明显；由图6(a)可知，随着kp的增大，谐振频率处及其附近幅值幅度变化不大，而输出频率小于谐振频率时系统幅值幅度逐渐增大，说明增大kp，有利于提高系统在低频段的跟踪性能。

由图5(b)可知，随着ki的增加，谐振频率处增益和谐振带宽均不断增大，谐振频率处幅值幅度增大，有利于消除系统稳态误差，但谐振带宽增大将使无用信号放大，不利于系统的稳定性；由图6(b)可知，随着ki的增加，系统谐振频带变宽，无用信号被放大，系统输出性能和稳定性降低。

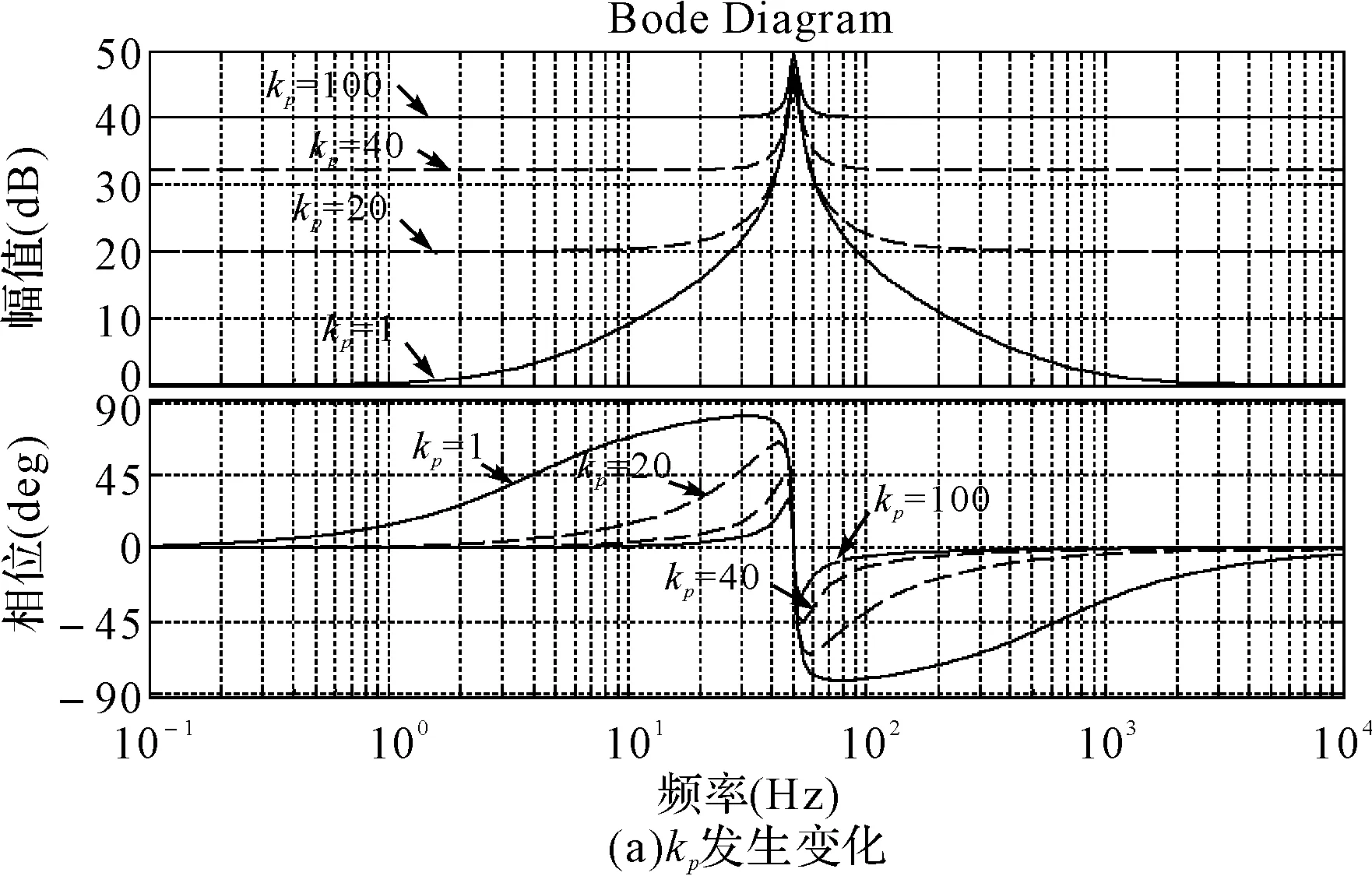
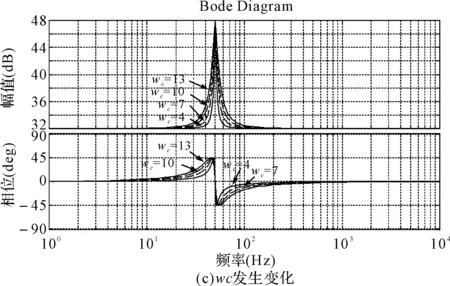
图5 实际PR控制器GPR(s)频域响应

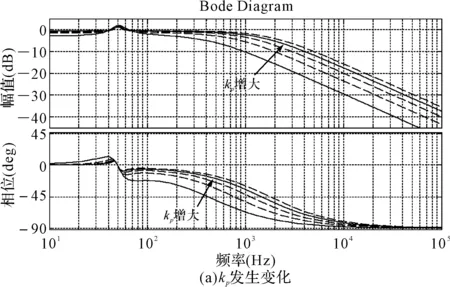
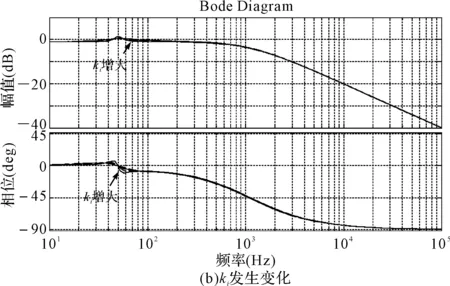
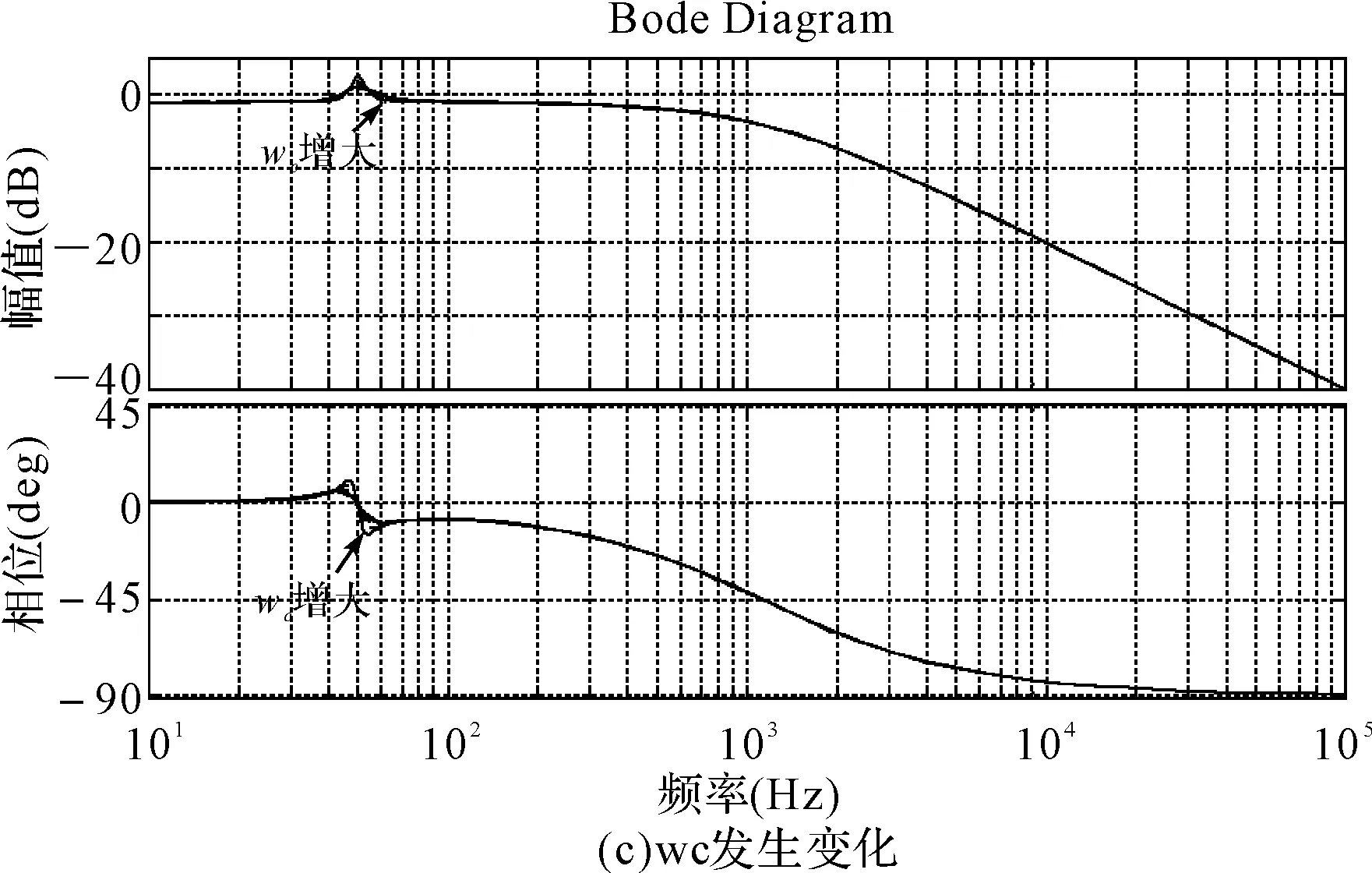
图6 系统闭环传递函数频域响应

由图5(c)随着ωc的增加，谐振频率的带宽不断增加，但在谐振频率点处增益变化不大，说明ωc主要是决定系统谐振频率带宽，ωc太小，系统抗扰动能力弱，ωc太大，容易把无用信号放大，系统输出电流谐波含量增大；由图6(c)可知，随着ωc的增加，系统谐振频带变宽，无用信号即输出频率附近电流含量增加，输出电流谐波变大。

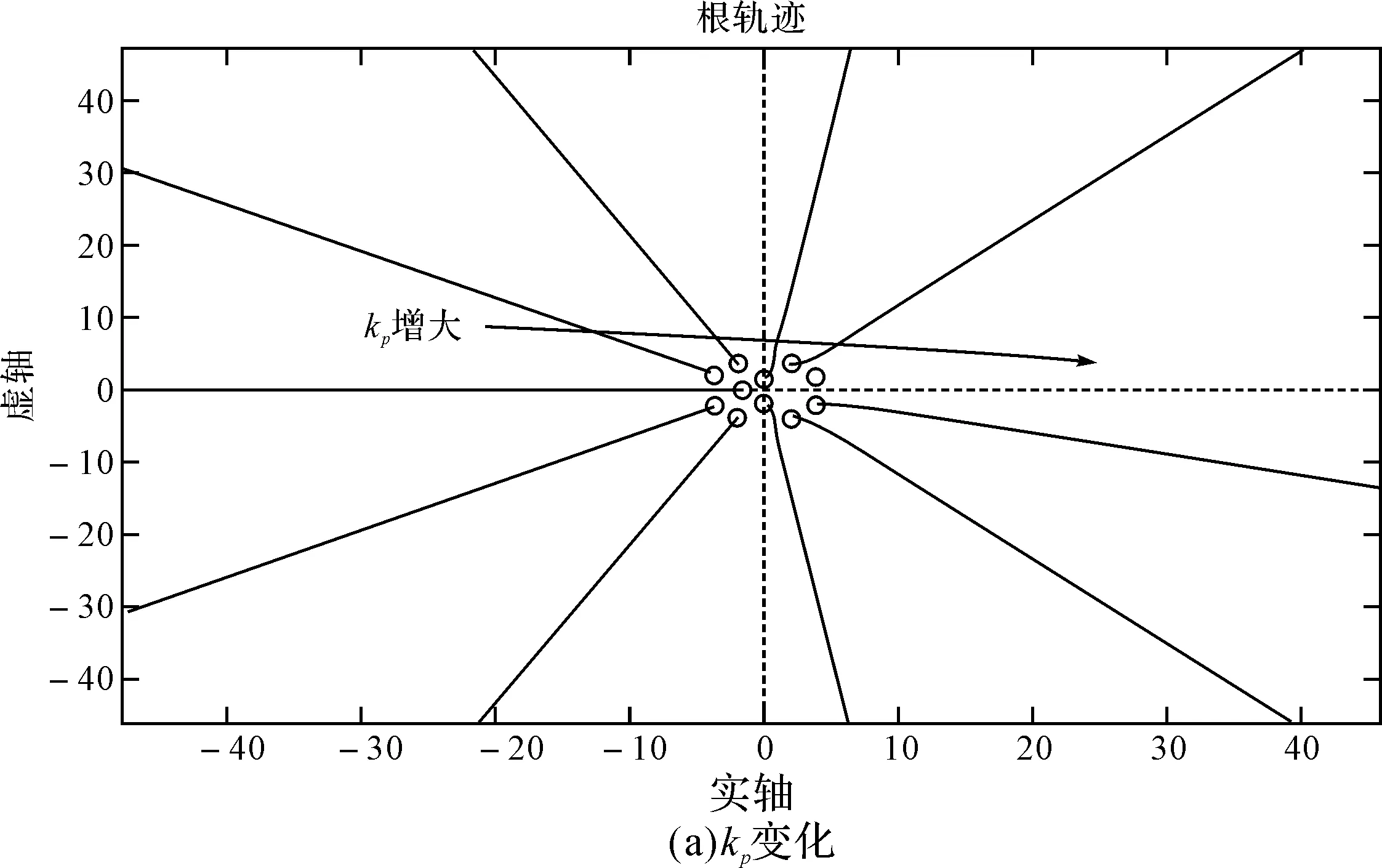
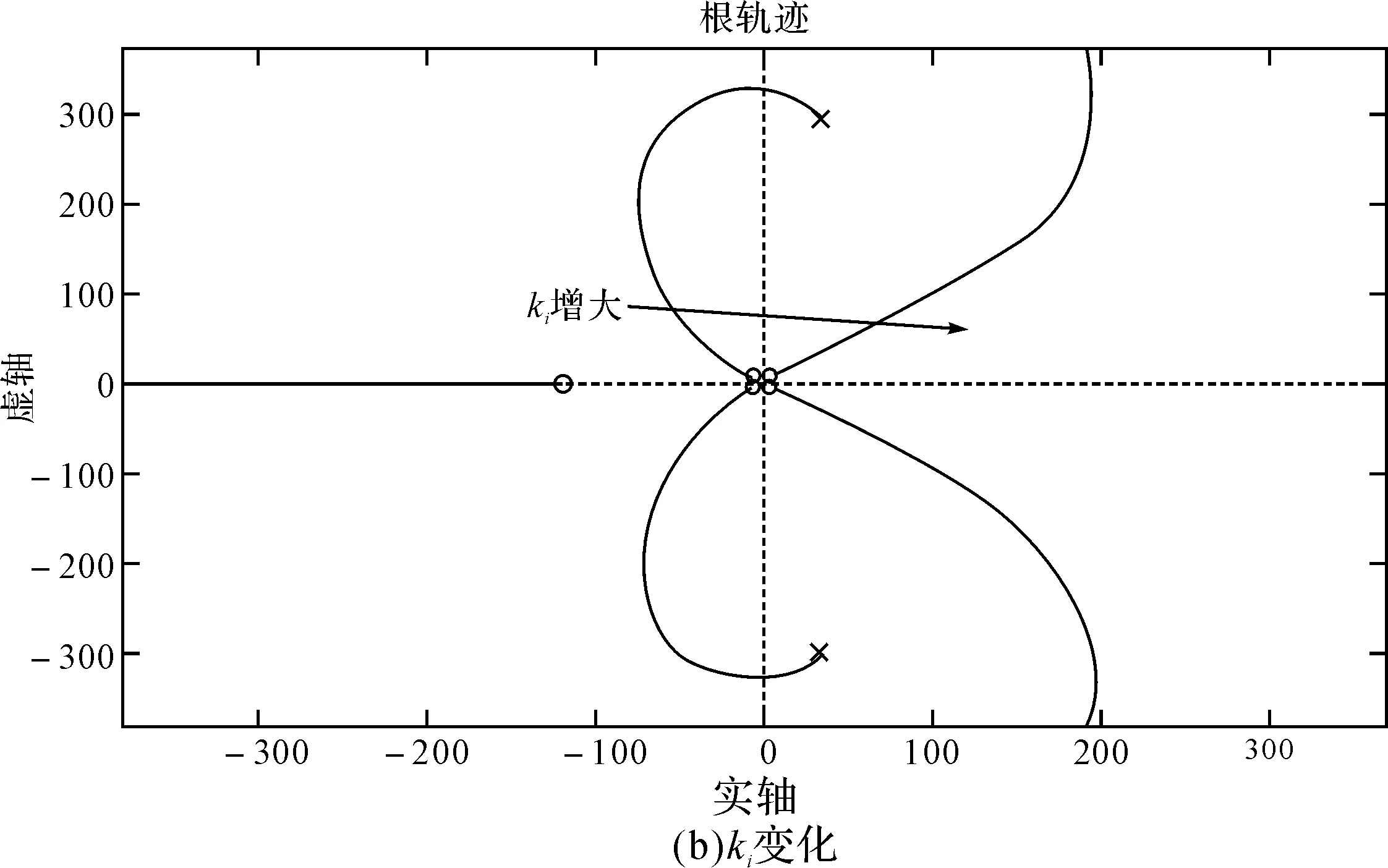
图7 kp、ki取不同值时系统极点分布

图7(a)中kp由20变化到80，图7(b)中ki由200变化到1000。由图7可知，随着kp、ki的增大，系统的极点逐步向右半平面转移，说明系统的不稳定性逐渐增加。因此，kp、ki取值时，应以保证系统稳定作为前提。

本文以输出电流频率50Hz作为研究对象，由图6可知，当kp=60、ki=200和ωc=10rad/s时，系统谐振频率在50Hz附近，不仅实现了输出电流能够准确跟踪输入电流，同时可确保系统的稳定。因此，将其作为改进PR控制器的参数。

4 仿真研究与试验验证

4.1 仿真研究

利用Matlab软件搭建了直接型矩阵变换器的仿真模型，参数设置见表1。

表1 直接型矩阵变换器仿真参数

图8和图9分别为频率变化(15Hz→30Hz→50Hz→25Hz)时输出电流跟踪指令电流、0.1s时给定电流幅值突变为8A时输出线电压UAB、A相参考电流和输出三相电流仿真结果。由图8、图9可知，在稳态时输出电流很好地跟踪了指令电流，当给定电流频率发生变动及给定电流峰值发生突变时，输出电流快速而准确地跟踪了给定电流，说明采用基于PR控制器的输出电流闭环控制，输出电流能够快速准确地跟踪指令电流的变化，具有较好的稳态结果和动态响应速度。仿真结果表明所将PR控制应用于矩阵变换器输出电流闭环控制以及所设计的PR控制器参数是切实可行的。

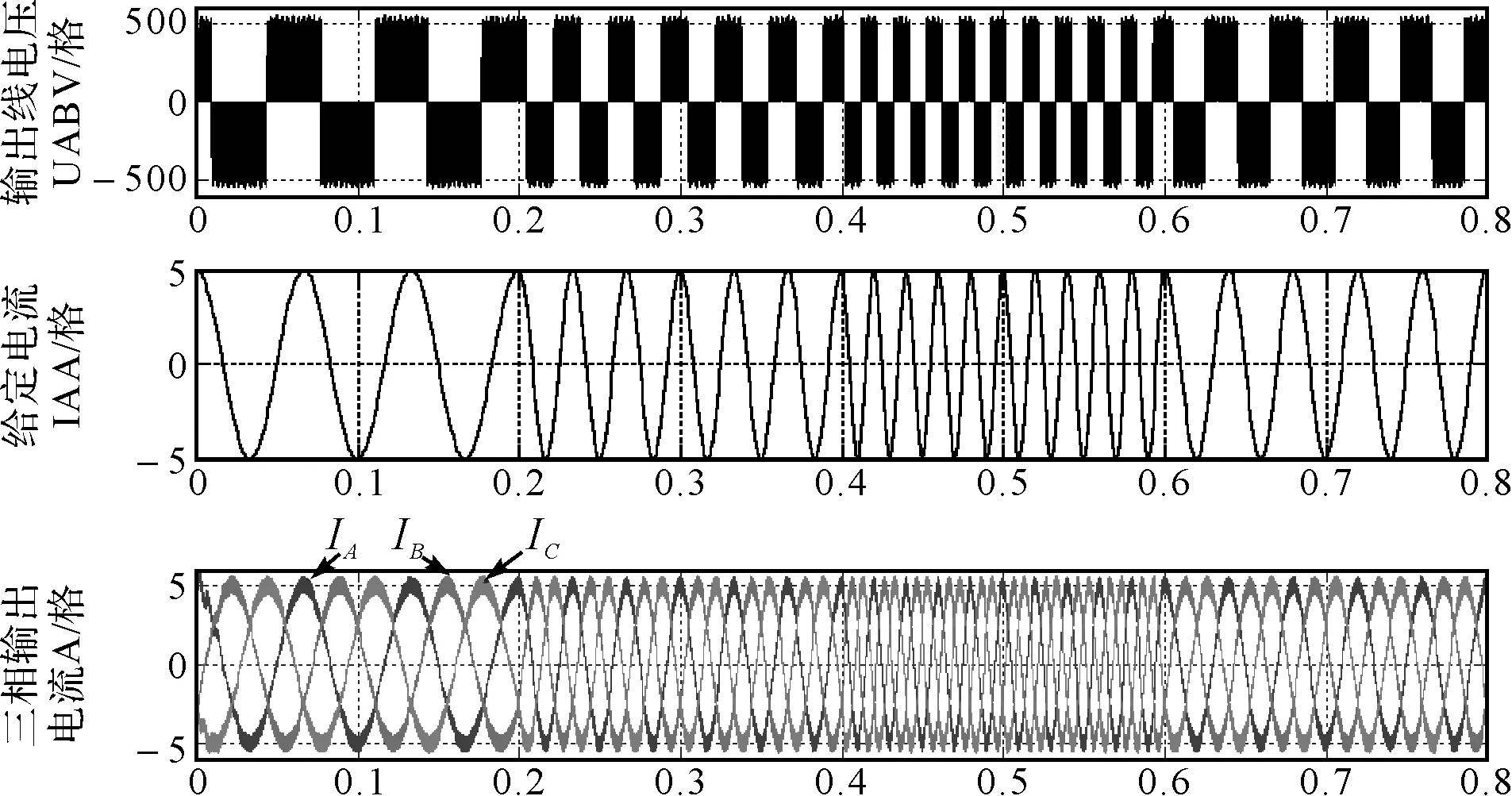
图8 输出频率变化时输出线电压、参考电流和输出相电流

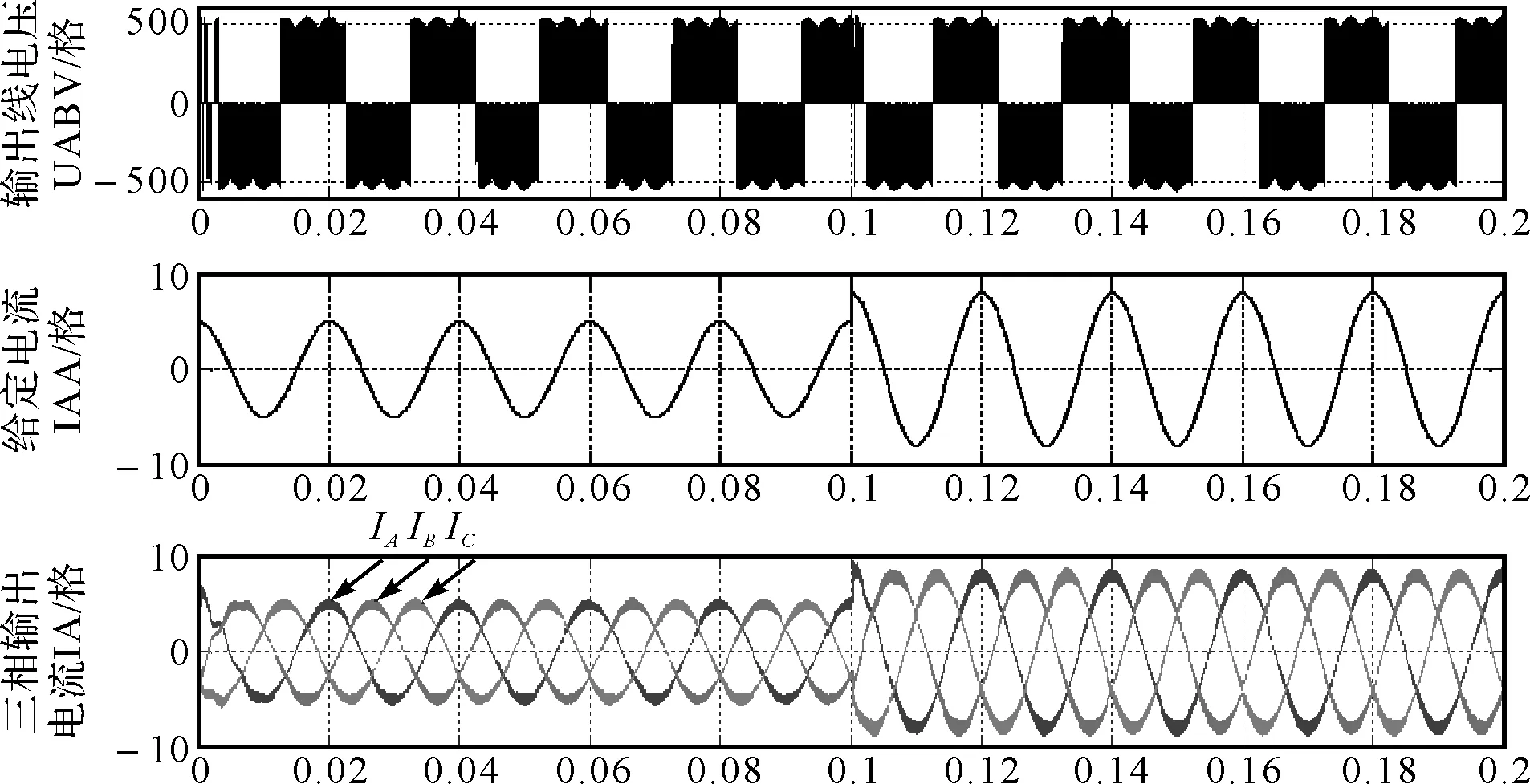
图9 0.1s输出电流峰值突变为8A

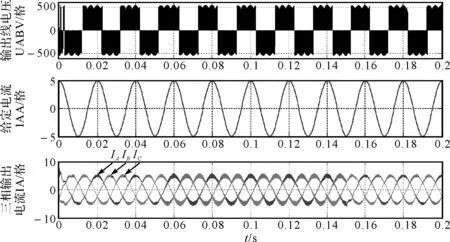
图10 0.05s突加负载和0.15s突卸负载输出线电压、参考电流和输出相电流波形

4.2 实验验证

在实验室搭建一5kW矩阵变换器样机进行实验验证，实验参数与仿真参数一致。图11、图12和图13分别为输出频率变化、输出峰值变化和负载变化时输出线电压、A相输出参考电流和A相与C相实际输出电流波形。

从图11～图13可以看出，无论是输出频率变化、输出电流峰值变化，还是负载变化，输出电流均较好地跟踪了参考电流指令，系统表现出良好的跟踪性能。实验结果与仿真结果基本一致，证明将比例谐振控制用于矩阵变换器输出电流闭环控制是切实可行。

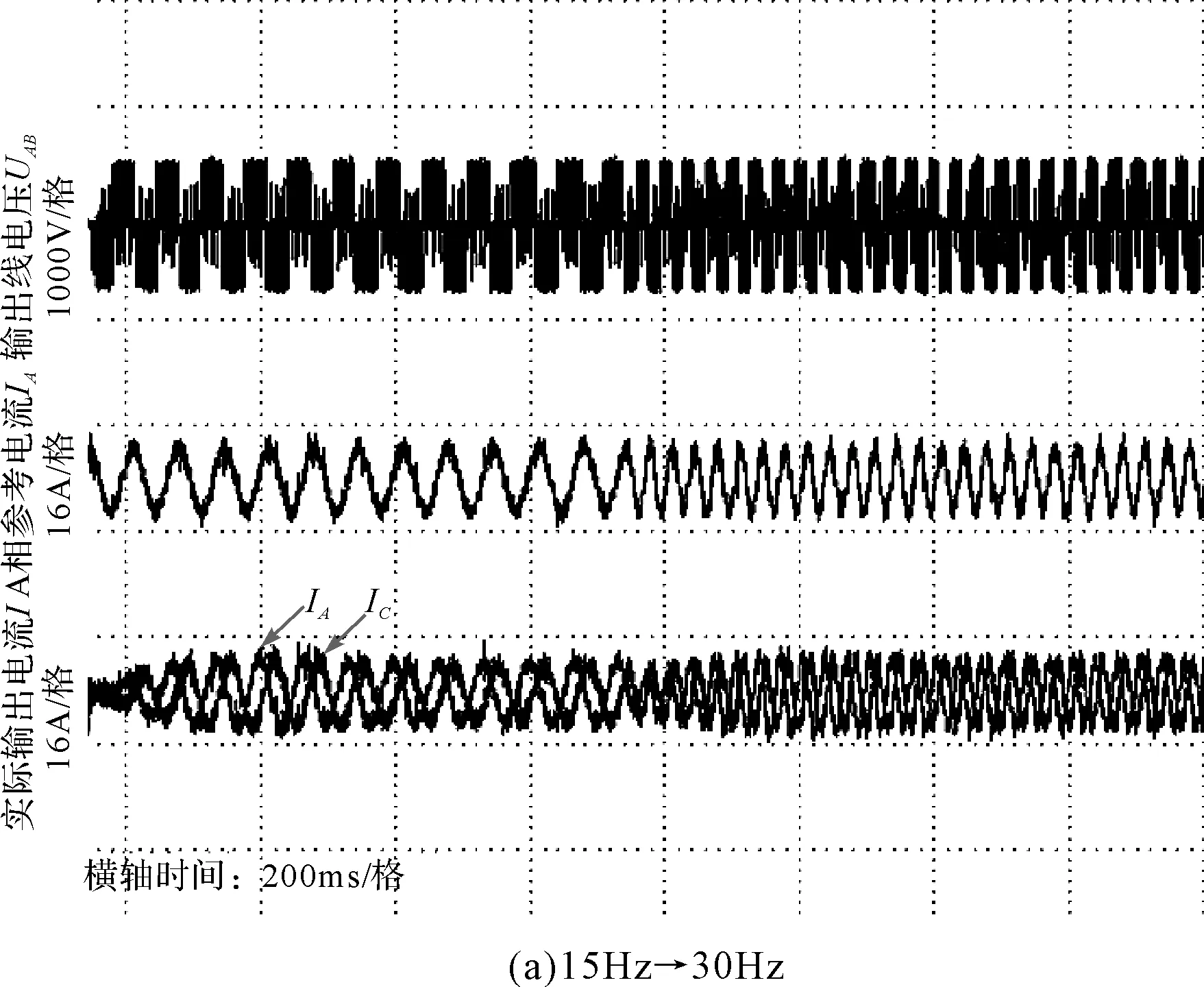
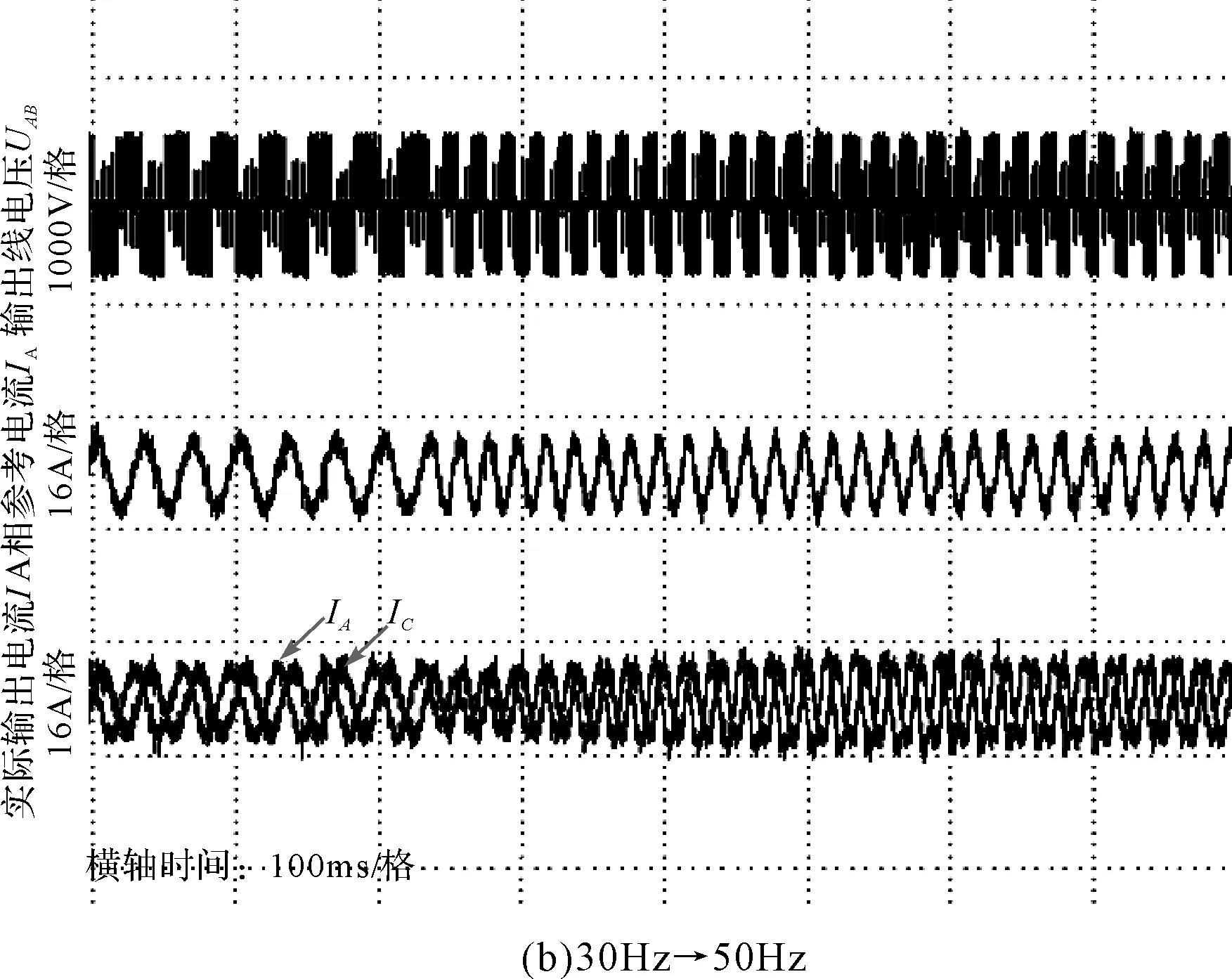
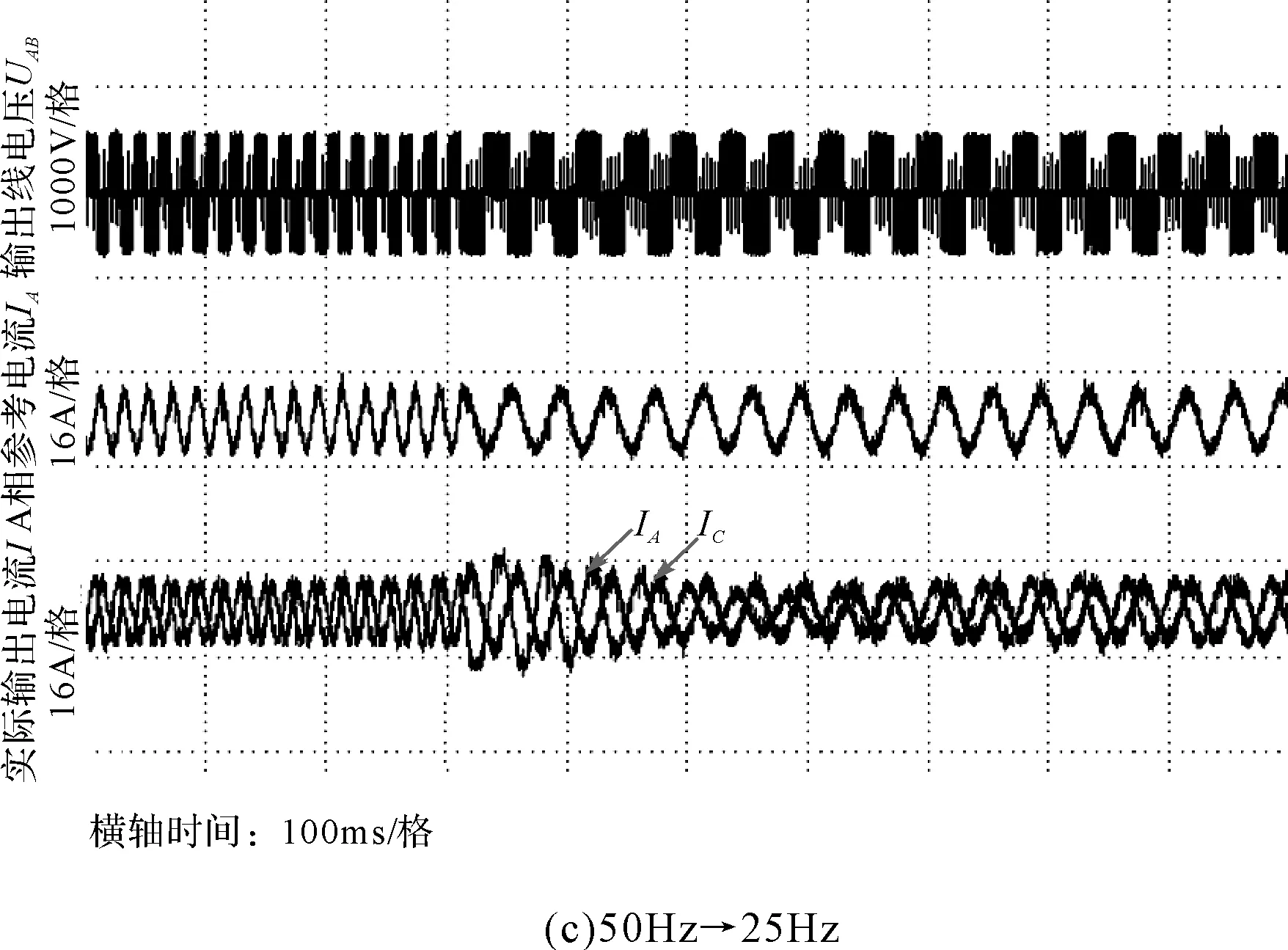
图11 输出频率变化时输出线电压、参考电流和输出相电流

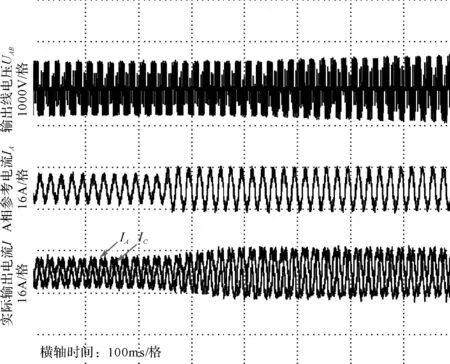
图12 输出电流峰值突变为8A

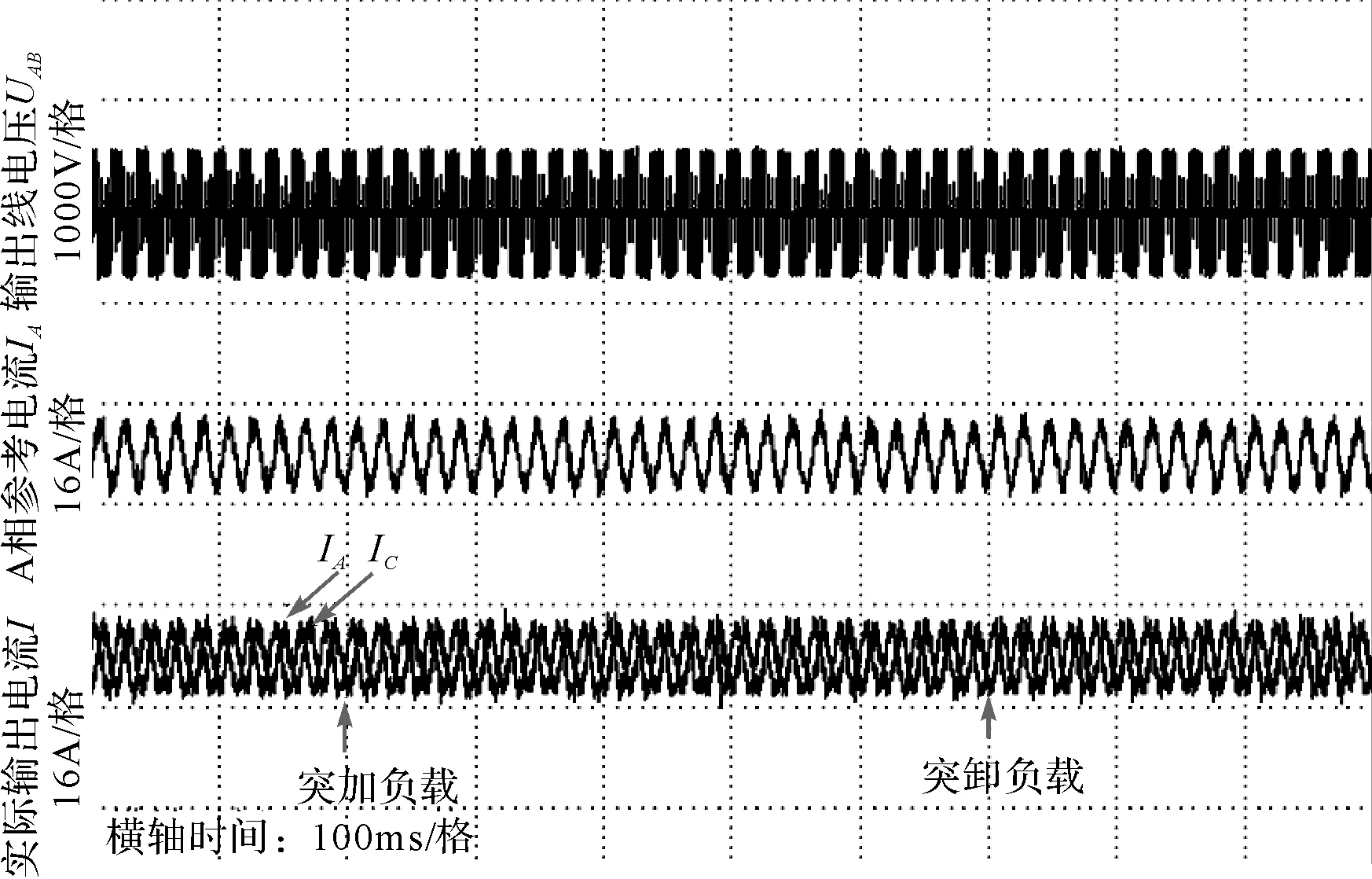
图13 突加卸负载输出线电压、参考电流和输出相电流波形

5 结语

本文将比例谐振控制引入到矩阵变换器输出电流闭环控制中，分析了比例谐振控制各参数对输出电流性能的影响，通过对其用于矩阵变换器输出电流闭环控制中进行仿真研究与实验分析可知：比例谐振控制一方面避免了PI控制复杂的坐标变换；另一方面可以实现输出电流动态响应快、零稳态误差的控制效果。实验结果证明了所提控制方法是正确可行的。

[1] Dan Xiao，Muhammed F R.Sensorless direct torque and flux controlled IPM synchronous machine fed by matrix converter over a wide speed range[J].IEEE Transaction on Industrial Informatics,2013,9(4):1855-1867.

[2] Zhang Xi.Sensorless induction motor drive using indirect vector controller and sliding-mode observer for electric vehicles[J].IEEE Transaction on Vehicular Technology，2013，62(7)：3010-3018.

[3] Xia Changliang，Zhao Jianxin，Yan Yan，et al.A novel direct torque control of matrix converter-fed PMSM drives using duty cycle control for torque ripple reduction[J]. IEEE Transactions on Industrial Electronics,1989,4(1):101-112.

[4] Kyo B, Frede B.Reduced-order extended luenberger observer based sensorless vector control driven by matrix converter with nonlinearity compensation[J]. IEEE Transactions on Industrial Electronics，2006，53(1)：66-75.

[5] 何必，张晓锋，林桦，等.采用零矢量补偿的矩阵变换器电流控制策略[J].中国电机工程学报，2007，27(13)：53-57.

[6] 马星河，赵军营，王旭东，等.矩阵变换器电流控制策略[J].电力自动化设备，2009，29(2)：56-59.

[7] Vargas R，Ammann U，Rodriguez J.Predictive approach to increase efficiency and reduce switching losses on matrix converters [J].IEEE Transactions on Power Electronics，2009，24(4)：894-902.

[8] Marco R，Christian R，Jose R，et al.Predictive current control with input filter resonance mitigation for a direct matrix converters [J].IEEE Transactions on Power Electronics，2011，26(10)：2794-2803.

[9] 李子欣，李耀华，王平，等.PWM整流器在静止坐标系下的准直接功率控制[J].中国电机工程学报，2010，30(9)：47-54.

[10] 周鑫，郭源博，张晓华，等.基于自适应跟踪控制的三相电压型PWM整流器[J].中国电机工程学报，2010，30(27)：76-82.

[11] 马林，金新民，唐芬，等.三相并网逆变器比例谐振控制机器网压前馈问题分析[J].电工技术学报，2012，27(8)：56-63.

[12] 杨云虎，周克亮，程明，等.单相PWM变换器相位补偿谐振控制方案[J].电工技术学报，2013，28(4)：65-71.

[13] 朱俊杰，马伟明，镊子玲.一种用于静止式中频电源的比例谐振控制策略[J].电机与控制学报，2012，16(10)：79-85.

Proportional Resonant Control Applied to Output Current of Matrix Converter

SUN Hongguang1XIA Yihui2

(1. Navy Representative Office in Dalian Area, Dalian 116021)(2. College of Electric Engineering, Naval University of Engineering, Wuhan 430033)

Compared to traditional PI control, proportional resonant control does not need complicated coordinate transformation, and there are no feed-forward compensation or coupling part effected by circuit parameters, which can achieve zero steady-static error to track sinusoidal referenced command and is widely used to AC-DC-AC converter. Based on analyzing the output circuit mathematical model of matrix converter, output current closed-loop control with proportional resonant is put forward. The output current control performance effected by proportional resonant control parameters is researched, and based on this proportional resonant parameters under a specific working condition are designed. Proportional resonant control applied to output current closed-loop control of matrix converter is emulated and experimented. Emulated results and experimental results both verify that the proposed method is right and feasible.

proportional resonant, current closed-loop, matrix converter, proportional integral

TM46

2016年9月7日,

2016年10月21日

孙宏光,男,硕士研究生,工程师,研究方向：舰船监造。夏益辉,男,博士研究生,讲师,研究方向：电力集成技术。

TM46

10.3969/j.issn.1672-9730.2017.03.013