广义Toda晶格方程的对称和精确解
李 红,王 鑫,李吉娜
(中原工学院 理学院,河南 郑州 450007)
广义Toda晶格方程的对称和精确解
李 红,王 鑫,李吉娜
(中原工学院 理学院,河南 郑州 450007)
本文主要研究了Blaszak-Marciniak结构方程广义Toda晶格方程的Lie对称和约化问题,并给出有理形式和指数形式的显式解.同时,给出序列的广义对称,进一步地证实其可积性.
广义Toda晶格;Lie对称;新显式解
1 引言
近些年,非线性离散孤子方程的研究引起研究者的广泛关注[1-4].连续孤子方程,可积非线性偏微分-差分方程等丰富了数学结构,例如,Lax对,无穷守恒定律,哈密顿结构,经典对称,广义或高阶Lie-Bäcklund对称[5-9]等等.其中,Lie对称[10]是寻求非线性偏微分-差分方程精确解的非常有效的方法之一,同时也可以预测可积性.
文献[11]在代数移位算子中采用r-矩阵形式,Blaszak和 Marciniak提出一个 m阶离散等谱问题:LmΨn=λΨn,Lm=Eα+m+uα+m-1Eα+m-1+…+uαEα,其中-m≤α≤-1,E是由Eun= un+1定义的移位算子.当m=3时,有如下形式的广义Toda晶格方程
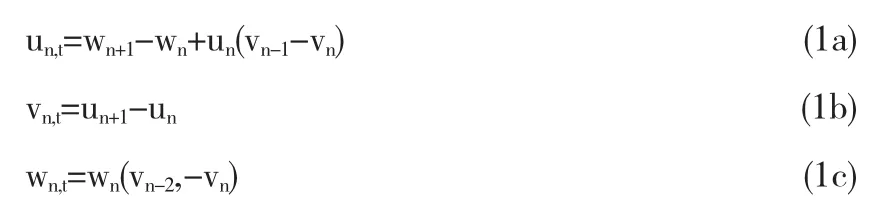
令wn=0,上述方程可退化为著名的Toda晶格方程.大量丰富的数学结构均与这个方程有关,例如哈密顿结构,Miura-like规范变换,可积辛映射,无穷守恒定律,Darboux变换等等.
本文的目的是求方程(1)的Lie点对称,然后方程可以简化为一个普通的微分-差分方程,找到有理形式和孤子形式的显式解.最后,给出序列的广义对称,更进一步证实其可积性.
2 Lie对称和幂零Lie代数
首先,我们介绍含有一个参数的连续点变换
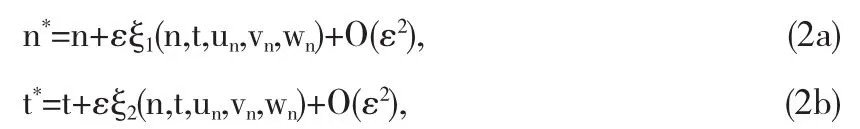
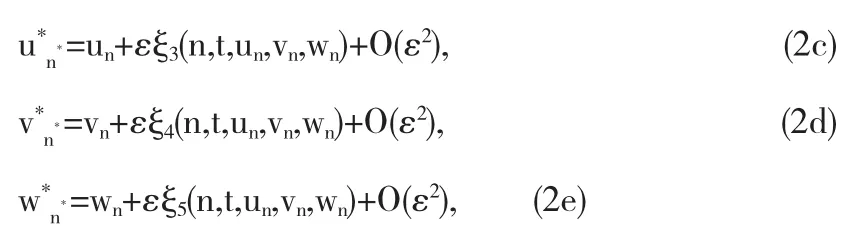
这里,无穷小生成元是
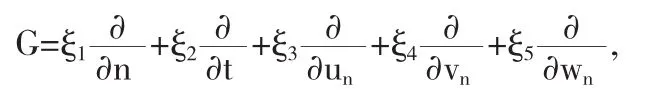
现在假设Blaszak-Marciniak晶格方程在这个变换下是不变的,也就是说

将方程(1)代入上式,得到
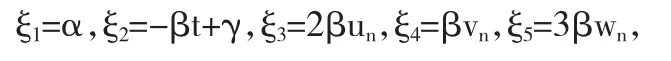
其中α,β,γ是任意参数,因此无穷小生成元是
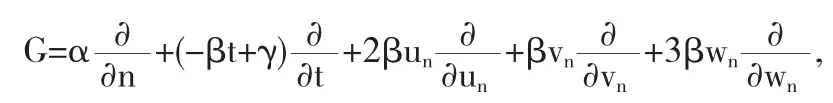
生成元G1,G2,G3是
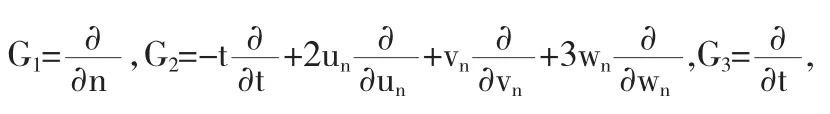
其交换算子如下:
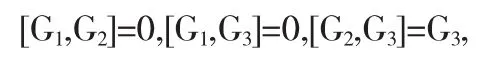
这表明Lie代数是幂零的.
3 约化和显式解
接下来,根据特征方程的对称,我们得到相似变量和相似变换
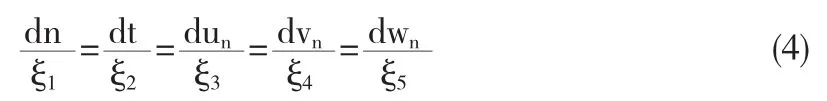
通过两种情况可以得到对称约化方程.
1)当β≠0,令
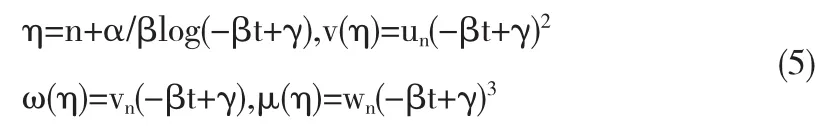
方程(1)可以约化为

2)当β=0,γ≠0,令
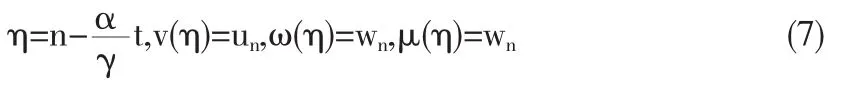
方程(1)可以约化为
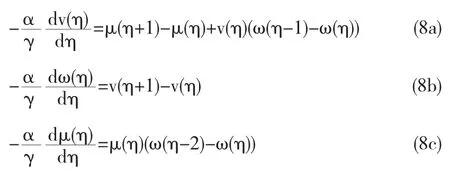
接下来得到β=0情况下的两个特解.
(i)有理解
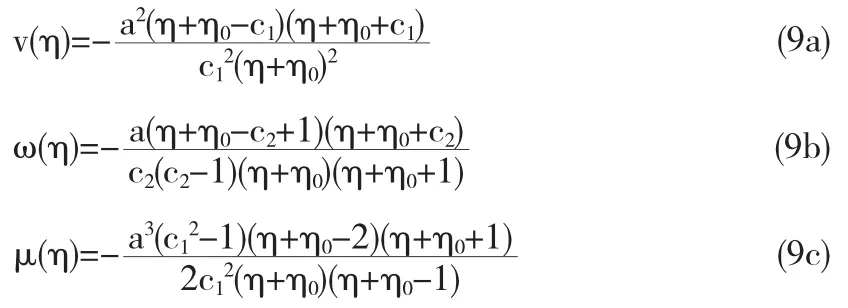
其中a=α/γ,c1,c2,η0是任意参数.

(ii)孤子解
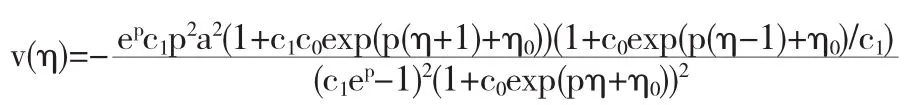
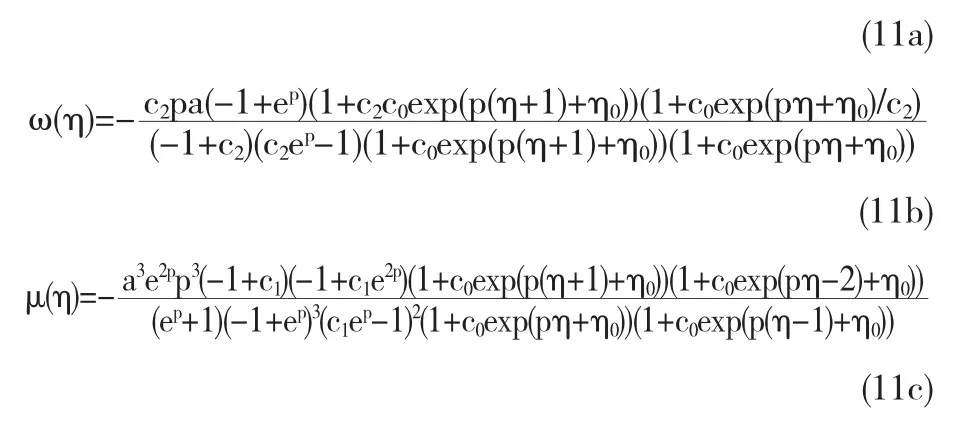
这里p,c0,c1,c2是任意参数,那么我们有
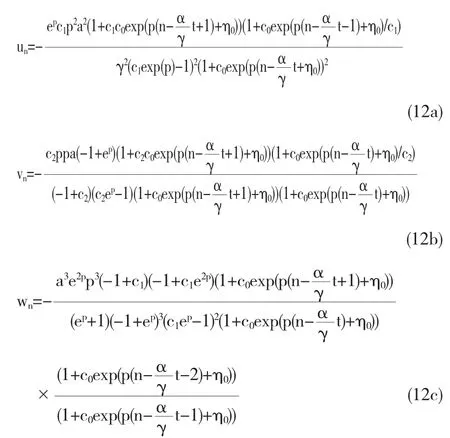
4 广义对称
在这一部分,我们通过Hereman等人提出的算法研究方程(1)的广义对称.首先,从生成元G2我们得到一个伸缩对称

un,vn和wn分别对应于关于t的二阶,一阶和三阶导数.也就是说,

接下来我们推导方程(1)秩为(3,2,4)的广义对称.秩为2,3和4的un,vn和wn的所有单项式构成形式如下
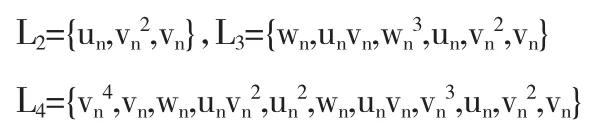
通过方程(1),可得

关于t的求导的单项式为
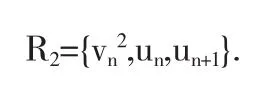
同样地,可得到
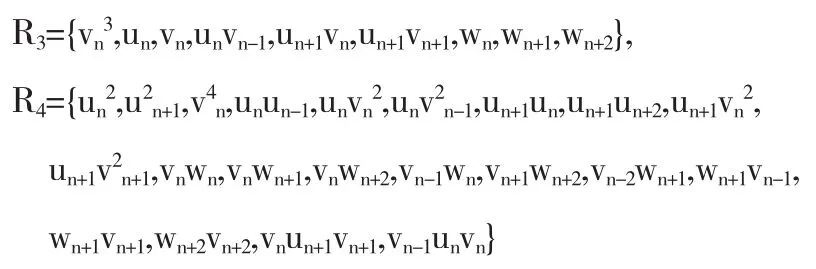
联合R3,R2和R4,可以得到如下广义对称

其中Dt是全导数,F1,F2,F3是方程(1)的右端项.接着就可以确定系数,且对称可以表示为

同样地,可以得到秩为(4,3,5)和秩为(5,4,6)的广义对称
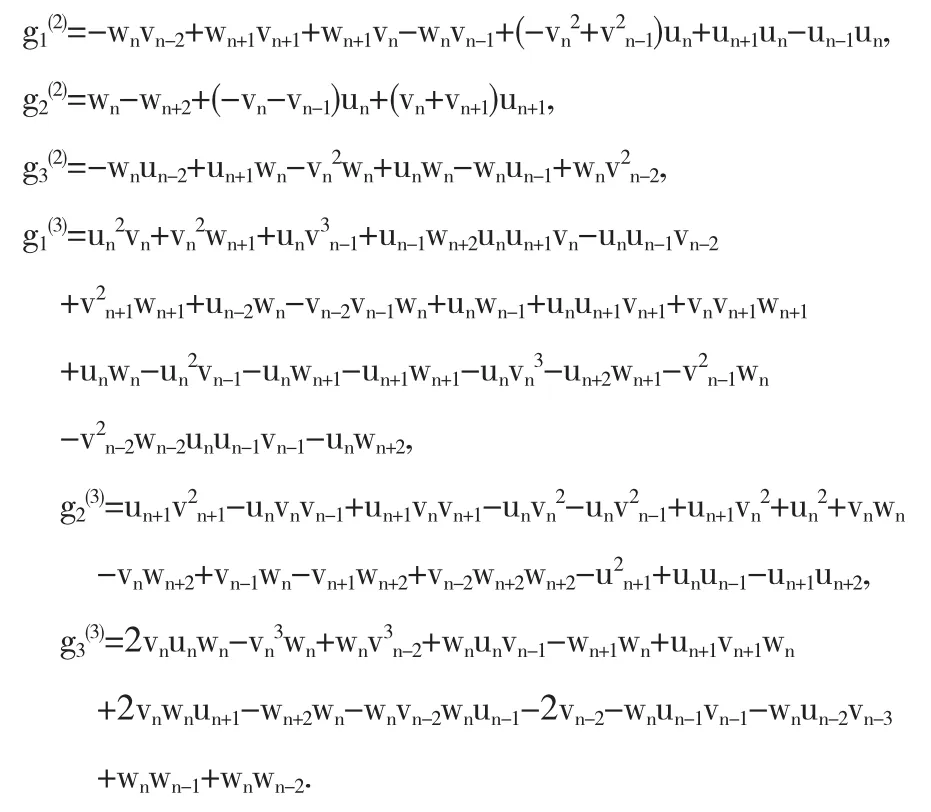
同样地,上述方法可以直接推广到高阶广义对称,这里不在赘述.
5 结论
在本文中,我们通过经典的Lie对称方法得到广义Toda晶格方程的Lie对称和约化,并给出有理形式和孤立形式的特解.如同其他BM分层晶格方程,我们得到方程(1)也有广义的对称序列,并进一步证实其可积性.此外,一旦得到方程的广义对称,利用Sahadevan和他的同事的研究,就可以进一步得到主要对称性和遗传算子,下一步我们将深入研究这类问题.
〔1〕Balakrishnan S.Similarity reduction,generalized symmetries,recursion operator,and integrability of coupled Volterra system[J].J.Math.Phys.,2008,49(11):737-754.
〔2〕Sahadevan R. Nonlinear differential-difference and difference equations:integrability and exact solvability[J]. Comput.Math.Appl.,2001,42(3-5):627-637.
〔3〕Blaszak M.Soliton point particles of extended evolution equations[J].J.Phys.A:Math.Gen.,1987,20(18): L1253-L1255.
〔4〕Wang X,Li Y Q,Huang F,Chen Y,Rogue wave solutions of AB system [J],Commun.Nonlinear Sci. Numer.Simulat.2015,20:434-442.
〔5〕Luo L,Fan E G.A Hierarchy of Differential-Difference Equations and Their Integrable Couplings[J],Chinese Physics Letters,2007,24(6):1444-1447.
〔6〕Zhang D J,Chen D Y.The conservation law of some discrete soliton systems[J].Chaos Solitons Fract.,2002, 14:573-579.
〔7〕WangX ,ChenY,DongZ Z,Symmetriesand conservation laws of one Blaszak-Marciniak four-field lattice equation[J],Chin.Phys.B,2014,23:010201.
〔8〕Xin X P,Chen J C,Chen Y,Nonlocal symmetries and explicit solutions of the Boussinesq equation[J], Chin.Ann.Math.B.,2014,35B:841-856.
〔9〕Qu C Z,Group classification and generalized conditional symmetry reduction of the nonlinear diffusion-convection equation with a nonlinear source[J], Studies in Applied Mathematics,1997,99(2):107-136.
〔10〕Olver P J,Applications of Lie groups to differential equations[M],Springer-Verlag,2000.
〔11〕Blaszak M,Marciniak K.R-matrix approach to lattice integrable systems[J].Journal of Math.Phys.,1994,35 (9):4661-4682.
O175.2
A
1673-260X(2017)03-0003-03
2016-12-21
河南省高等学校重点科研项目(15B110012,17A110036);河南省科技厅项目(152300410227)

