基于LBM和SEA的整车气动噪声及其传播分析与优化探索

刘功文吴海波周江彬陈蒨王毅刚

（1.上汽大众汽车有限公司，上海 201805；2.同济大学，上海 201804）

基于LBM和SEA的整车气动噪声及其传播分析与优化探索

刘功文1吴海波1周江彬1陈蒨1王毅刚2

（1.上汽大众汽车有限公司，上海 201805；2.同济大学，上海 201804）

针对某轿车气动噪声偏大的问题，基于格子波尔兹曼和统计能量分析法展开车内噪声计算。将分析结果与风洞试验进行对比，并依托准确的数值模型为基础，针对性地展开了造型优化。结果表明，该模型在主、客观评价体系中都能较好地符合实际噪声，对后视镜等外表面特征的优化可有效减小前侧窗表面的气压及声压脉动，削弱中高频的影响。该方法为整车风噪在产品前期开发阶段的概念设计及优化工作提供了一定的指导依据，可有效减少开发周期。

1 前言

车内听到的气动噪声（Aerodynamic Noise）根据噪声源不同主要分为泄露噪声（Leakage Noise）和风激励噪声（Wind Rush Noise）[1～2]。中低车速时，车内噪声主要来自发动机和轮胎，气动噪声的成分较小，但当行驶速度超过80 km/h后[1]，气动噪声逐渐占据主导地位。目前国内大部分公司在该领域的研究依赖于风洞或者实车道路试验，而关于气动噪声抱怨的解决也往往是在样车试制之后才展开相关的优化工作，但限于开发后期冻结的造型设计、高昂的开模及风洞试验费用，这种耗时耗资的产品开发手段所取得的效果非常有限。因而，在产品开发早期采用数值分析的方法对气动噪声性能进行预判分析和优化控制十分重要。

在数值计算领域，国内的夏恒[3]基于边界元（Boundary Element Method，BEM）和统计能量分析（Statistical Energy Analysis，SEA）相结合的方法，针对桑塔纳缩尺模型进行了车内气流噪声的理论计算，杨万里[4]采用大涡模拟模型（Large Eddy Simulation，LES）和Lighthill-Curle声学模拟理论预测了车外场点的噪声特性，汪怡平[5]通过大涡模拟计算了汽车外部瞬态流场并采用FW-H声学模型预测噪声特性。目前国内的研究主要基于传统的CFD方法，只能得到噪声源附近的外场声学信息，并不能直接计算车内的声场数据。

Francois[6]则采用格子波尔兹曼方法（Lattice Boltzmann Method，LBM）进行非稳态流场的激励求解，并通过侧窗的振动声学传递预测了不同传递模块对车内噪声不同频段的贡献程度；David[7]结合LBM和SEA对由外后视镜引起的气动噪声进行了相应的分析和优化工作；Robert[8]则对底盘引起的噪声展开了有效的试验和数值分析工作，对比了不同车速和风向倾角工况的拟合数值。

本文针对风激励噪声开展数值计算，并基于LBM得到整车非稳态的外流场激励分布，综合考虑声学边界条件，采用SEA求解车内声场，获得了车内噪声主观评价（响度）和客观评价（A计权声压级）数值结果，并与实车风洞试验数据进行趋势验证。基于较为精确的数值分析模型和早期计算结果，有针对性地开展了对外后视镜及三角窗盖板的结构造型优化工作。

2 格子波尔兹曼理论

传统的CFD方法都是从纳维-斯多克（Navier-Strokes,N-S）方程开始，它是一组描述流体流动行为的偏微分方程。对于大多数实际的流体问题来说，这组方程是封闭的，具有高度的非线性及多自由度复杂性，直接求解需要大量体积单元来计算包括声源和响应点在内的局部流体特性，在实际中受到计算容量和时间限制，一般只适用于很小的流体区域和低频声学问题。因此，实际中常采用间接方法，分为求解简化的非定常可压缩流体的N-S方程及基于莱特希尔声学相似理论或其同类理论求解结构表面非定常动力压力脉动两部分，也就是将宏观控制方程离散，然后使用数值方法求解离散方程。

LBM是建立在分子运动和统计力学基础上的一种模拟流场的数值理论。在这种数学方法的基础上，LBM用粒子的微观速度反映流体的运动，该理论函数包含了一组常数，形成了每个粒子在其所在位置和相邻位置之间的连接，因此能够精确地计算对流，可实现用最大的时间步长产生最小的数值耗散，并从微观动力学的视角，将流体的宏观运动近似为大量微观粒子运动的平均统计数值。

LBM的理论公式为[7]：

式中，fi为粒子在i方向的运动方程，并对应一组离散速度矢量ci，i=0,1,2…；CiΔt为空间增量；Δt为时间增量；为粒子碰撞项。

为简化说明，假设Δt=1，并对式（1）中的碰撞项采用最简化和常用的Bhatnagar-Gross-Krook（BGK）形式来表示：

式中，τ为松弛时间参数；为基于局部流体动力学特性的均衡分布函数。

在对湍流波动进行建模时，BGK公式采用有效湍流松弛时间参数τeff替代τ进行修正，τeff可由重整化群（Renormalization Group，RNG）理论公式获取[9]：

3 统计能量分析法

SEA是目前用于处理中高频噪声的常用分析手段，其基本思路是根据自然边界及模态振型等条件将复杂系统分解成不同的模态群或若干个相互独立的子系统，以便于统计能量分析。

分解到每个子系统的能量等于该系统耗散的能量与子系统之间的传递能量之和，通过求解各子系统之间的能量耗散与输入功率之间的线性方程组，即可得到单一子系统的平均能量。

子系统能量平衡方程为[10]：

式中，Pk,in为子系统k的输入能量，ω为振动角频率；分别为子系统k、j储存的平均总能量；ηkj为子系统k输入子系统j的耦合损耗因子。

其中：

式中，ηk为子系统k的内损耗因子。

将式（4）转换成矩阵形式为：

4 全尺寸风洞噪声试验

4.1 试验布置及环境

整车气动噪声试验[11]使用的风洞为3/4开口回流式风洞，喷口面积27 m2，背景噪声（无风状态计权100～10 000 Hz，车内24.57 dB（A））符合气动声学测试要求。

试验现场如图1所示，试验车放置在风洞驻室天平转盘的中心位置，测试过程中边界层的抽吸和移动带系统处于关闭状态。4个座椅位置安置人工头用于采集双耳噪声信号，如图2所示。

图1 整车气动噪声试验测试环境

图2 声学探测人工头布置

4.2 试验工况及数据

为确保试验的准确性，在正式测试前需对人工头信号进行校核，并在左后视镜侧一定距离的外场布置麦克风作为信号参考。测试时将车身外表面（除上、下进气格栅）的缝隙及沟槽用胶带密封，为避免增大额外的传声损失，所用胶带均为0.3 mm的高质量布基胶带。密封区域包括四门、四窗、前风窗玻璃、外开手柄及外后视镜等，并通过比较整车有、无密封状态下的噪声曲线来分离泄露噪声和风激励噪声（或外形噪声）。

图3为风速120 km/h、风向倾角0°工况时驾驶员头部空间测试所得的车内A计权声压级曲线。由图3可以看出，车内噪声在250 Hz以后呈下降趋势，1 000～3 150 Hz高频段的泄露噪声占主导地位，在1 600 Hz处峰值尤为明显，总噪声值为46.63 dB（A），其中泄露噪声为45.64 dB（A），外形噪声仅为39.74 dB（A）。在中低频区间，外形噪声占据绝对优势，其曲线特征几乎与车内总噪声特性吻合，在3 150 Hz处的外形噪声曲线有一个明显突起峰值，幅值为37.96 dB（A）。

图3 驾驶员头部气动噪声的频率特性曲线

在1/3倍频程曲线中，仅将100～10 000 Hz频段的声压级能量纳入计算，得到3组类别的总值对比如图4所示，就噪声总幅值而言，外形噪声贡献占主要地位。

图4 驾驶员头部气动噪声

5 整车气动噪声数值计算

5.1 计算思路

本文数值计算结果均以车内驾驶员头部空间（左耳与右耳的平均值）的噪声值表示，在不考虑底盘噪声的情况下，轿车的风激励噪声主要来源为A柱、外后视镜、刮水器、外开手柄、行李架及B柱等附近区域的压力脉动[7～10]，如图5所示。而车辆高速行驶时，由外部造型引起的流场区域的波动能量又主要分为气压波动（Wall Pressure Fluctuation）和声压波动（Acoustic Pressure Fluctuation）两部分，两类外部激励源共同作用并主要通过前风窗玻璃和侧窗向车内传递噪声[6]。

图5 风激励噪声传播原理

根据上述噪声传播原理，数值计算过程分为两步：基于LBM方法的CFD非稳态流场计算，分别得到结构输入激励和声学输入激励；基于SEA法的车内声场计算。

如图6所示，结构输入激励由路径A经玻璃-气压的振动耦合向车内辐射噪声，而声学输入激励则由路径B经玻璃-声压的振动耦合及声透射两个分支向车内辐射噪声。

图6 数值分析框架

5.2 非稳态流场计算

数值计算采用与风洞试验车相同的数模，为了计算精确，应尽可能使整车网格贴合实际情况：其中上、下进气格栅开放，同时模型包括发动机舱的动力总成、冷却系统及管路等结构，底盘作粗糙包络处理并考虑刮水器和落水槽等细节，总计面网格899万个，空间体网格5 126万个。整车流体计算网格建模如图7所示。

图7 整车流体计算网格

流场的敏感区域，如A柱、翼子板上端和后视镜等处的几何细节更需精细，以捕捉微小的涡流变化，最小面网格尺寸达到了1 mm，而发动机罩及车身翼子板网格尺寸在5～15 mm之间，其它网格则在15～25 mm之间。

在保证精度的前提下，为节省计算时间，采用不同的网格加密区域（VR）来划分空间网格区域，包括A柱、外后视镜、刮水器、格栅等风激励噪声敏感区域，如图8所示。图9为后视镜附近分层的VR空间网格区域，覆盖区域有落水槽、刮水器、翼子板上端、A柱下端及外后视镜前、后区域并直达B柱。

模拟过程中，分析模型放置在长方体的虚拟风洞之中，计算域总长约25倍车长，总宽约40倍车宽，总高约30倍车高，并在空间计算区域内划分5层非等间距VR计算空间，同时在车身外表面生成2层包络区域，如图10所示。

图8 车身外表面VR

图9 后视镜区域的空间VR

图10 虚拟风洞空间计算域

本次数值计算使用PowerFlow进行求解，由于入口流速较高，此处采用可压缩理想流体。边界条件设置：入口设置为速度，风速120 km/h，风向角0°；出口设置为压力出口；轮胎滑移带静止状态；总分析步数设置为187 060。

5.3 SEA车内声场计算

SEA方法处理风激励噪声的出发点是表面声压（气动波和扩散声波）。气动波产生于对流气体，并与结构模态耦合，传递能量，引起结构振动和声辐射；扩散声波部分通过结构透射声向车内传递噪声。车外流场的压力波动向玻璃等板件产生的能量输入为：

式中，Re为雷诺数；P*为波动压力；v为速度；Ω为板件面积；x为坐标位置；ω为振动角频率。

在进行车内声场计算时，将驾驶舱沿中央通道划分成12个单独的空间计算区域，包括前、后排乘员的脚部、躯干和头部，如图11所示。SEA计算的声学边界条件（如玻璃阻尼损耗因子及车内混响时间等参数）均由试验获得。

图11 SEA车内空间子系统划分

取120 km/h（0°倾角）时的驾驶员头部空间噪声试验值与数值计算曲线对比如图12所示，主、客观评价对比为响度（试验值为16.70 sone，计算值为13.83 sone）和声压级（试验值为63.14 dB（A），计算值为59.17 dB（A））。在100～315 Hz中低频段，试验值与计算值相差较大，幅度在2.74～7.14 dB（A）范围内，这主要是由于目前数值暂时无法考虑中低频段的底盘噪声以及SEA方法在中低频噪声区间计算精度较差两方面因素综合引起的，但该段的总体波动趋势二者基本吻合。

图12 驾驶员头部外形噪声的对比

需要指出的是，3 150 Hz处形成的高频峰值与风窗玻璃的吻合频率有直接的关联性。如果假设侧窗玻璃为无限大的平板，均匀平板吻合频率的近似理论公式[1]为：

式中，fc为吻合频率；h为均匀平板厚度。

该车侧窗玻璃厚度为3.85 mm，由式（8）可得近似的理论吻合频率为3 247 Hz，与计算结果接近，也从侧面验证了数值模型的准确性。

综合上述对比，该整车模型可有效拟合实际风激励噪声的趋势水平，为后续外形结构的优化工作奠定了可靠的数据基础。

5.4 云图分析

对计算结果可采用直观的三维视图来捕捉涡流的附着、分离及再附着过程，帮助分析噪声的产生机理及影响区域，找到可能的噪声源及优化方向。

图13所示为对时间平均的流体压力系数为零的等值区域，代表了在流场瞬态中涡流的分离区域。由图13可知，气流波动对车内噪声的传递主要来自A柱及后视镜区域，而作用在侧窗上剧烈的压力波动主要源于涡流的分离和再附着的综合结果。

图13 压力系数为零的等值区域

A柱及后视镜附近的流场可借助图14所示的时域涡流强度及压力分布云图来描述，选择滤波范围500～6 000 Hz，涡流的强度、形状及脱离过程都可直观地获得。在时域动态图中可知，流经翼子板和A柱处的涡流直接冲击后视镜内棱角及支架等处，压力陡然增高，流速变大，剧烈的压力波动沿后视镜内侧面的引导方向冲击后视镜盖板及侧窗左下侧外表面。

图14 涡流压力脉动云图

图15为驾驶员侧的车窗外表面压力波动云图，其中颜色越深的区域能量激励越大。取1/3倍频程中的176～353 Hz频段切片说明，图中除了常见的A柱涡流分离区能量均布集中外，在侧窗左下侧（外后视镜支架斜后方）也呈现了极高的压力波动现象，这也验证了上文提到的涡流流向带来的激励冲击问题。因此，后期的优化方向也应围绕涡流能量传递路径中的后视镜及其盖板展开，并有效规避或削弱其能量的冲击。

图15 驾驶侧侧窗外表面压力脉动云图

6 风激励噪声优化探索

基于风洞实车噪声测试，针对占主导影响成分的外形噪声展开后续的结构优化工作。但为寻求切实可行的改进方案，减少后续造型样件及油泥模型风洞试验成本，借助模型进行前期开发阶段的风激励噪声性能虚拟优化设计。

前文针对数值计算的流场云图，已经提供了对外后视镜及其盖板展开结构改进的工作思路。在不改变外后视镜人机位置的前提下，经过多轮模型尝试，仅对两处结构做出细微调整，如图16所示。新造型1对侧窗附近的后视镜安装盖板在垂直玻璃方向降低一定高度；新造型2将外后视镜支架变薄。

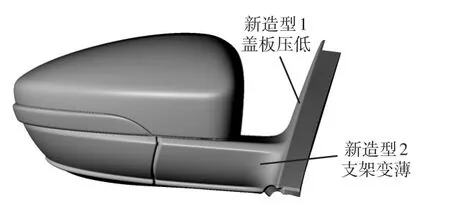
图16 结构调整

取驾驶员左耳对比说明，最终优化结果与原造型的数值曲线对比如图17所示，新造型1较原模型在低频段声压级幅值略大一些，但在1 000～4 000 Hz的高频带能取得明显的优化效果，其中1 600 Hz处差值达到3.16 dB（A）。新造型2则基本在全频段上都能取得良好的优化效果，尤其在100～500 Hz的中低频及1 250～2 500 Hz的高频处均取得了良好的改进，差值最大的两处出现在125 Hz及1 600 Hz，分别为1.78 dB（A）和2.27 dB（A）。

图17 驾驶员头部噪声对比

车内噪声客观评价总声压级从59.39 dB（A）分别降至59.09 dB（A）和58.18 dB（A），主观评价的响度从13.83 sone分别降至13.45 sone和13.01 sone。这说明，从数值计算的角度有针对性地从源头对外后视镜及其盖板的局部调整能够取得一定的成效，但优化幅度及趋势是否准确还有待于后续的改进试验加以验证。

7 结束语

结合格子波尔兹曼方法和统计能量法对整车风激励噪声数值建模可对车内噪声取得较好的前瞻性预测，尤其是高频的A计权声压级曲线波动趋势与试验相比吻合度较高。

对气动噪声的研究，基于风洞试验可在产品开发前期确定影响噪声的主要因素，分离出泄露噪声与外形噪声，并为下一步的虚拟优化设计提供一定的指导。

针对噪声源头及传递路径改进的思路，在数值建模计算中得到了很好的验证，较小的调整措施也可能取得良好的效果，本文的总声压级从最初的59.17 dB（A）最多可下降到58.18 dB（A），响度从13.83 sone最多减小至13.01 sone，后续还需要进一步的试验验证。

1 庞剑，湛刚.汽车与发动机振动噪声理论与应用.北京：北京理工大学出版社，2006.

2 傅立敏.汽车设计与空气动力学.北京：机械工业出版社，2013.

3 夏恒，宫镇，陆森林，等.关于高速车辆内部气流噪声计算方法的研究.汽车工程，2003，25（1）：78～81.

4 杨万里，李明江，刘国庆.乘用车风噪声模拟研究.华中科技大学学报（自然科学版），2005，33（11）：77～79.

5 汪怡平，谷正气，李伟平，等.汽车气动噪声数值计算分析.汽车工程，2009，31（4）385～388.

6 van Herpe F,D’Udekem D,Jacqmot J,et al.Vibro-Acoustic Simulation of Side Windows and Windshield Excited by Realistic CFD Turbulent Flows Including Car Cavity.International Styrian Noise,Vibration and Harshness Congress: the European Automotive Noise Conference，Graz，2012.

7 Lepley D J,Graf A.A Computational Approach to Evaluate the Vehicle Interior Noise from Greenhouse Wind Noise Sources.SAE International，2010.

8 Powell R,Moron P,Balasubrammanian G.Simulation of Underbody Contribution of Wind Noise in a Passenger Automobile.SAE International Journal of Passenger Cars-Mechanical Systems，2013，6（2）：1251～1261.

9 Yakhot V,Orszag S A.Renormalization group analysis of turbulence I Basic theory.Journal of Scientific Computing，1986，1（1）：3～51.

10 Chen H,Kandasamy S,Orszag S,et al.Extended Boltzmann kinetic equation for turbulent flows.Science，2003，301（5633）：633-636.

11 贺银芝，杨志刚，王毅刚.汽车车身密封对车内气动噪声影响的机理及试验研究.汽车工程，2012，34（8）：692～695.

（责任编辑 斛 畔）

修改稿收到日期为2016年6月6日。

Analysis and Optimization of Vehicle Aerodynamic Noise and Propagation Characteristics Based on Lattice-Boltzmann Method and SEA

Liu Gongwen1,Wu Haibo1,Zhou Jiangbin1,Chen Qian1,Wang Yigang2
（1.Shanghai Volkswagen Automotive Co.,Ltd,Shanghai 201805;2.Tong Ji University,Shanghai 201804）

A vehicle emitted louder aerodynamic noise at high speed.To solve this problems,numerical calculation was carried out based on Lattice-Boltzmann and Statistic Energy Analysis(SEA).Meanwhile analysis results were compared with full-scale wind tunnel vehicle test,and styling optimization was carried out based on accurate calculation model.The results showed that this model could well simulate actual wind noise in both the subjective and the objective evaluation system,and rear view mirror optimization could effectively reduce aerodynamic and sound field pressure fluctuation on the front side window,inner sound pressure level curve was obviously weakened at middle-high frequency band.This method provided some guidance for vehicle wind noise design and optimization in predevelopment stage which could effectively shorten development cycle.

Lattice-Boltzmann,SEA,Aerodynamic noise,Aerodynamics,Full-scale wind tunnel test,Structural optimization

格子波尔兹曼 统计能量分析法 气动噪声 空气动力学 全尺寸风洞试验 结构优化

U461；TB53

A

1000-3703（2017）02-0038-06