平面多边形面积的最大值

福建省南平市高级中学(353000) 郑定华

平面多边形面积的最大值

福建省南平市高级中学(353000) 郑定华

在我校2016届高三的一次数学模拟考中,一道看似并不起眼的试题,而答题结果却一败如水,这是为什么呢?

题目已知平面图形ABCD为凸四边形(凸四边形即任取平面四边形一边所在的直线,其余各边均在此直线的同侧),且AB=3,BC=5,CD=6,DA=4,则四边形ABCD面积S的最大值为( )

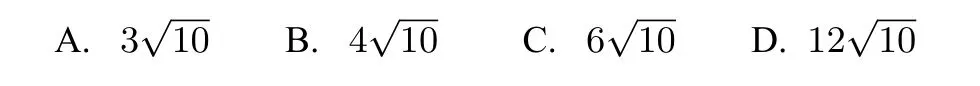
究因这是一道已知四边形的四条边长,求其面积的最大值问题,答案是C.解该题时,入口单一,只能用直接法求解;思路难找,对学生的分析与综合,转化与化归等能力的要求都较高;技巧性强,解答中有颇多的曲折地方,分明就是一道以选择题形式包装的综合题,挑战题,难怪学生折戟.

图1

思考平面四边形面积的最大值能否由其四条边长来表示?此时的四边形又有何特点?

结论1 在平面四边形ABCD中,AB=a,BC=b, CD=c,DA=d,p=(a+b+c+d),则当且仅当对角互补,即其四个顶点共圆时,这个四边形的面积取得最大值,此时

证明如图1,在△ABC和△ADC中,由余弦定理得AC2=a2+b2-2abcosB=c2+d2-2cdcosD

又平面四边形ABCD的面积S=S△ABC+S△ADC=,所以

注在四边形ABCD中,若边AD退化为一点A,则d=0,就得三角形面积的海伦公式

推论周长为定值的四边形中,正方形的面积最大.

证明设四边形的周长为定值1,其四条边的长分别为a,b,c,d,则p=(a+b+c+d)=,由结论1知

当且仅当对角互补时,①式等号成立.又因为

综上知,当且仅当对角互补且四边相等,即这个四边形为正方形时,面积最大.

平面n边形也有类似的美妙性质

结论2 对于平面n边形A1A2···An(n≥4,n∈N),当且仅当其n个顶点共圆时,面积最大.

证明(1)当n=4时,由结论1知,结论2成立.

(2)假设当n=k(k≥4,k∈N)时,结论2成立,即对于平面k边形A1A2···Ak(k≥4,k∈N),当且仅当其k个顶点共圆时,面积最大.下面证明：

对于k+1边形A1A2···AkAk+1(k≥4,k∈N),当且仅当其k+1个顶点共圆时,面积最大,用反证法.

假设k+1边形A1A2···AkAk+1(k≥4,k∈N)的面积最大时,其k+1个顶点不共圆,则两组顶点A1A2···Ak和A2···AkAk+1中,至少有一组不共圆.

不妨设A1A2···Ak不共圆,由归纳假设知,此时的k边形A1A2···Ak的面积不会最大.保持各边长不变,A1Ak边不动,适当调整各个内角的大小,当顶点A1,A2,···,Ak共圆时,k边形A1A2···Ak的面积最大,此时的k+1边形A1A2···AkAk+1(k≥4,k∈N)的面积就比原来的面积大,这与假设矛盾,故假设不成立,由此知,对于k+1边形A1A2···AkAk+1(k≥4,k∈N),当且仅当其k+1个顶点共圆时,面积最大.

根据(1)和(2),对一切n≥4,n∈N,结论2成立.

由结论2还易知有如下的推论：

推论边长相等的n边形以正n边形的面积最大.

应用

用结论1解我校试题：

例1(河北省衡水中学2015届高三下学期期中考数学试题(理))已知平面图形ABCD为凸四边形(凸四边形即任取平面四边形一边所在的直线,其余各边均在此直线的同侧),且AB=2,BC=4,CD=5,DA=3,则四边形ABCD面积S的最大值为( )

例2 把一条长为1的铁丝围成一个四边形,则这个四边形面积的最大值为___.

解由结论2知,当且仅当所围成的四边形是正方形时,其面积最大,此时的边长为,其最大面积为.