经历圈点子图到列表计算促进学生理解算理
——队列表演一(两位数乘两位数)教学实践和思考
甘卫星
【课前思考】
学生在三年级上册学习两、三位数乘一位数后已有利用点子图圈一圈、算一算的经验,教材为什么在这里又用一节课内容让学生利用点子图研究两位数乘两位数的计算方法?不断让学生积累这样的操作经验究竟用意何在?这样的编排究竟对学生理解算理有什么帮助?会不会对队列表演二(竖式计算)有帮助?让学生经历从直观运算到算法运算的抽象过程,对学生理解算理非常重要,而点子图是能让教师读懂学生思维的有用媒介。学生在点子图直观运算的基础上,再用横式记录计算的过程和结果,引导学生体会列表计算是点子图计算的抽象形式。
课前提问,问题1:借助点子图探究14×12的直观运算,并用横式记录计算的过程和结果;问题2:理解点子图的乘法运算与列表的乘法计算之间的联系和区别;问题3:鼓励学生应用问题1和问题2中掌握的方法进行计算,起到巩固所学新知识的作用。
【教学实践】
一、读懂情境,提出问题,估算感知
1.教师出示教科书中的情境图,鼓励学生解读图中蕴含的数学信息。
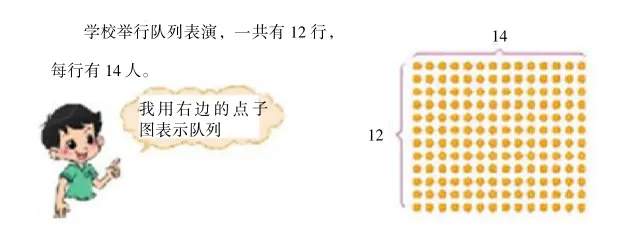
师:从这张队列表演图中,你们了解到哪些数学信息?
生:一共有12行,每行有14人。
师:根据这两条信息,你们能提出什么数学问题?
生:一共有多少人?
师:想一想可以怎么列式?
2.学生估计,引入新课。
师:估计一下,这一队列大约是多少同学?
生:大约是150人,把14看作 15,把 12看作 10,15×10=150人。
生:肯定超过140人,把12看作 10,14×10=140 人。
师:今天这节课我们就来研究学习《两位数乘两位数》。
【设计意图:本环节的设计直接呈现材料,通过学生观察、思考,提出问题。重点凸显学生估算猜测,教师不但要关心学生估算的答案,更要关心学生有没有主动投入到“估算”中去。让学生通过估算,提高对数的感知和直觉思维能力,同时也使学生明确要解决的问题。】
二、自主学习,顺应理解,交流讨论
1.独立思考,书面记录解决的方法。
师:借助作业纸上的点子图,先圈一圈,再列式计算。
2.小组交流,选派代表发言。
(1)以四人小组为单位交流,每人在小组内表达自己的方法,并注意倾听同伴的发言,在表达与倾听中比较不同的计算方法。
(2)小组推选一位代表发言,先在小组里试讲一遍,准备班级交流。
(3)教师巡视收集连乘(14×6×2),整十数和一位数相加(10+2)的点子图,表格式,竖式或典型的错误,用记号笔标上呈现的序号。
3.班级交流,展示方法。
(1)小组展示。
师:哪个小组来给大家介绍一下你们小组的方法,讲清是怎样圈的,又是怎样算的?
小组代表1:我是这样圈的,把12分成两部分,每一部分都是6行,先算14×6=84(人),再算84×2=168(人)。
师:大家听懂了吗?刚才这位同学是把12分成2个6,也就是把12拆成了6乘2,先算14乘6,再把结果乘2。
(板书:14×6×2=168)
小组代表2:我是把12行圈成三部分,每部分是四行,我先算 14×4=56(人),再算 56×3=168(人)。
师:你们刚才都把12拆成了几乘几,能不能把14也拆一拆?
师:在点子图中可以怎么圈呢?
小组代表3:我是把每行14人分成两部分,每一部分都是7人,我列出的算式是12×7×2=168(人)。
(板书:12×7×2=168)
小组代表4:我是把12分成两部分,一个圈了10行,一个圈了2行,我是先算 14×10=140(人),再算14×2=28(人),最后算140+28=168(人)。
(2)比较方法。
师:这几个小组在计算方法上有什么共同的特点?
生:都是把两位数乘两位数转化为以前学过的两位数乘一位数。小组1、2、3是把一个两位数拆成两个一位数相乘;小组4是把两位数拆成整十数和一位数相加,再把两位数乘整十数和两位数乘一位数的结果加起来。
【设计意图:学生独立思考后,在小组内讲述自己的解题方法,再通过班级小组代表的交流,整理解决问题的多种方法和思路。两位数乘两位数的主要依据是乘法分配律复合运用的过程。通过学生圈一圈,再算一算,让学生借助点子图这个抓手直观体验,进行详细的分解,理解算理,培养学生的交流和归纳能力。】
三、比较联系,凸显算理,抽象提升
1.对比两种方法,理解算理。
(教师出示一位同学的圈法,要求学生仔细观察,读懂之后再举手发言)
生:这种方法是把12行分成2行和10行,把每行的14人分成10人和4人。
生:这样分以后要算五次。
师:打开课本第32页,下面的方法你能看懂吗?结合点子图说一说。

(学生独立思考)
师:谁来给大家说一说你的理解?
生:表格的第一行是把14分成10和4,左边的一列是把12分成10和2,100就是10×10=100,40 就是 10×4=40……
生:这种表格式就是课本上的第三种圈法。
(学生结合点子图说计算方法,教师出示课件)
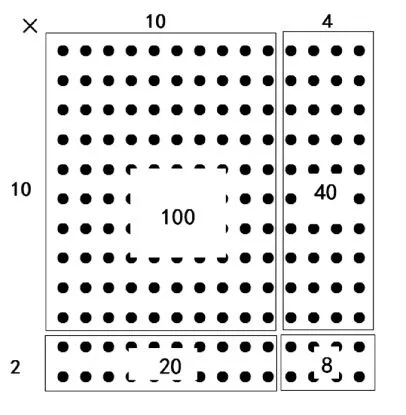
师:表格式其实就是简单版的点子图,请把32页上两个点子图列成表格。
师:列表格的计算比点子图简洁,表示更清晰。
2.尝试练习,体验算理。
计算课本第32页“算一算”,学生反馈交流。
【设计意图:通过理解点子图和问题2的表格式,让学生理解表格中的数据是如何得到的,明白表格中的数据和点子图及算式的联系,表格式的算法就是点子图抽象的过程。让学生经历知识的形成过程,圈点子图和列表格的计算方法体验肯定会对研究乘法竖式的算理有很大的帮助,同时为学习三位数乘两位数打下基础。】
四、多样练习,巩固算法,当堂检测
1.填一填,算一算。
23×13= 14×11=
2.选择答案。
□2×□4的结果是:
A.586 B.390
C.□8 D.□□8
3.数学历史:介绍《算法统宗》中讲述的一种“铺地锦”的乘法计算方法,这种方法就是用格子来算的。
4.小组检测,评比最佳小组(完成作业,小组长批改小组作业,评出最佳小组)
【设计意图:通过练习检测巩固所掌握的方法,介绍“铺地锦”的古代计算方法,体验圈点子图和列表格的方法。最后通过最佳小组的评价来完成课堂作业本的练习,提高学生的学习的积极性。】

