践行有序思维培养探究能力
——以浙教版“组合图形面积练习课”的一道习题为例
林
【教学内容】
浙教版五年级上册第76、77页组合图形面积练习2第1题。
【教学过程】
一、独立尝试
1.下图中,四边形ABCG和CDEF都是正方形,它们的边长分别是8厘米和6厘米。在这个图中作三角形,要求选择正方形的三个顶点,构造出不同的三角形,并分别计算出它们的面积。
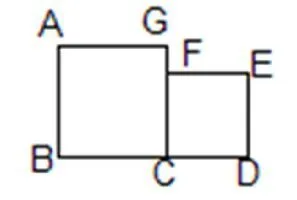
2.找出面积相等的三角形,将序号按面积分类。
面积是( )平方厘米的是( )。
3.尝试将所画出的三角形分类,并写出分类标准。
()归为一类,原因是( )。
【设计意图:教师通常会把这道题只当作三角形面积计算练习,学生能正确计算所画三角形的面积就结束了。本节课的设计中,把这个环节放到课前,让学生充分地去画和算各种不同的三角形。学生水平各异,画的个数也不尽相同,但无论画出几个,都要让学生观察、整理,找到分类的依据。】
二、讨论探究
1.分类标准。
教师引导:同学们昨天都画了一些三角形,如果要给这些三角形分类,你打算怎么分?
(按面积、按三角形角和边的类型、按三角形在正方形里面还是正方形外面、按三角形在一个正方形里面还是横跨两个正方形……)
师生交流后再次引导:我们主要研究面积相等的这种分法。大家想一想,底和高都相等的三角形面积一定相等吗?如果三角形的面积相等,那么它们的底和高是不是一定相等?
【设计意图:分类的标准见仁见智。在学生发言的基础上,聚焦“面积相等”的分类方案,将面积相等的三角形的各种形态作比较和研究,找到底和高的共同之处,帮助学生理解“等底等高的三角形面积相等”这一规律。】
2.分类整理。
通过讨论,我们已经知道了三角形底和高都相等的三角形面积一定相等,请找一找面积是24平方厘米的三角形有哪些?
小组交流:
(1)汇总:面积是24平方厘米的三角形。
(2)整理:整理汇总的三角形,找出一定的规律。
汇报情况预设:
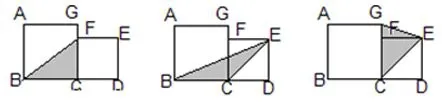
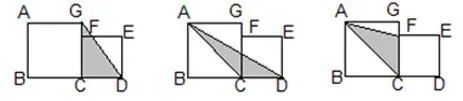
(3)想一想,怎样去找不重复不遗漏?
【设计意图:选取面积是24平方厘米的三角形作为例题研究,让学生观察这些三角形的底和高,以及图形相互之间的联系,找到有序思考的方法:固定一条底边,再分别找符合条件的顶点构成三角形。】
3.用这样的方法,你还能整理出其它面积的三角形吗?
小组合作:
(1)连接三个顶点所画的三角形有哪几种不同的面积?
(2)小组成员分工,分类研究。
(3)汇总交流,看看其他成员是否有补充。
(4)准备汇报,怎样让别的小组明白你们思考的方法?
汇报情况预设:
面积是6平方厘米:
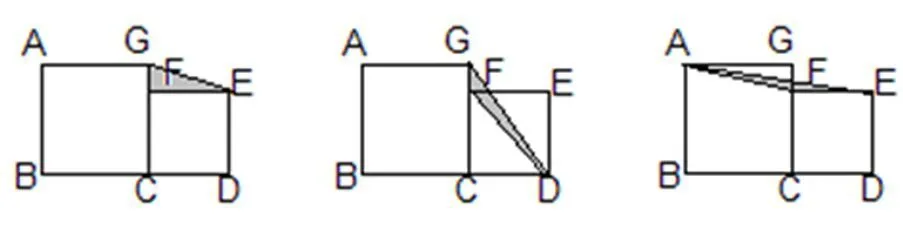
面积是8平方厘米:

面积是18平方厘米:
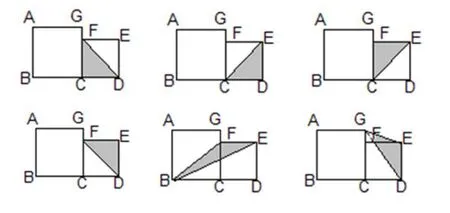
面积是32平方厘米:
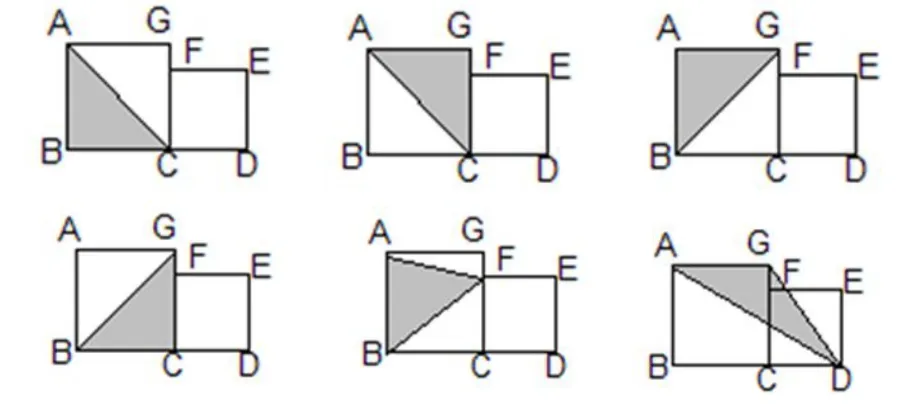
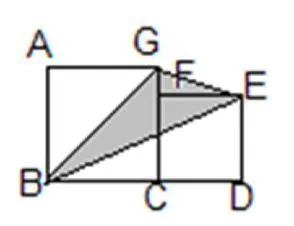
(如果没有这种情况就到后面处理)
面积是42平方厘米:
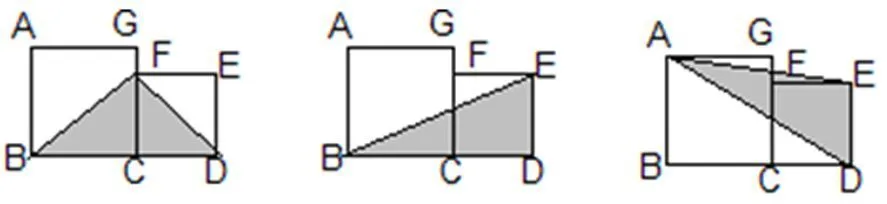
面积56平方厘米:
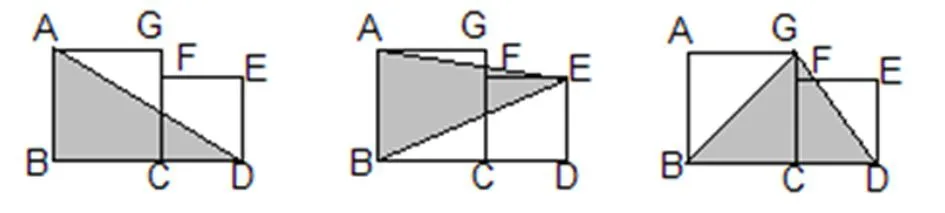
4.下面这些三角形的面积怎么计算?你有哪些不同的方法?

转化成等底等高的三角形再计算面积,总面积-空白部分面积=阴影部分面积。
【设计意图:例题讲解结束后,让学生分组研究其他的三角形,希望能通过集体的力量,弥补个人在课前思考的不足,在交流协作中每个人的认知都进一步得到拓展和提升——特别是ΔACE、ΔBGE、ΔADF等,其底和高不在正方形边上,需要转化后求取面积。学习能力稍弱的学生可以借机了解和掌握求阴影部分面积的更多方法。】
三、延伸拓展
教师引导:我们按面积分类,画了那么多三角形,是不是所有的可能都画完了呢?究竟连接正方形的三个顶点,可以构造的不同的三角形一共有多少个呢?
讨论:七个顶点连接其中的三个,有多少种可能?
生:7×6×5=210(个)。
生:有重复,210÷6=35(个)。
师:有没有连接后,不能形成三角形的呢?
生:顶点在同一直线上的不可以。B、C、D和G、F、C就不能组成三角形。35-2=33(个)。
师:和我们刚才画图的方法比照一下,你有什么发现?
确定字母 A、B,分别连接 C、D、E、F、G;
确定字母 A、C,分别连接 D、E、F、G;
确定字母 A、D,分别连接E、F、G;
确定字母A、E,分别连接F、G;
确定字母A、F,连接G;
然后确定字母 B、C,分别连接 D、E、F、G;
然后确定字母B、D,分别连接E、F、G;
……
【设计意图:本课结尾,简单讲讲用组合的方法推算一共可以组成多少个三角形。与前面的枚举形成呼应和对照。展示同一个数学问题,可以从不同角度去思考,不同的思考过程有不同的思维体验和知识应用,培养良好的数学观。】
四、课后探究
如果在图中连接四个顶点组成四边形,有多少个不同的四边形?你能把它们分一下类吗?能求它们的面积吗?有兴趣的同学可以去试一试,也可以组成小队一起去挑战一下!
【设计意图:为学有余力的学生提供素材,使之能够运用本课所学知识,去解决更多的变式问题。】
【教学反思】
该教学内容是浙教版五年级上册第76、77页组合图形面积练习课中的一道习题。在教学中,教师从引导学生找“面积是24平方厘米”的三角形的底和高入手,先构建出“同底等高面积相等”的三角形,进而引导构建出“等底等高面积相等”的三角形,让学生充分感知三角形面积相等的规律。通过整理发现:有部分三角形并不能直接利用等底等高计算面积,引导学生通过等积变形转换成等底等高的三角形以求出面积,真正将“等底等高三角形面积相等”这个知识点做实,做活。在学生自主研究的基础上,教师紧紧抓住“有序思考”进行点评和深化,启发学生先固定一条边,然后去找符合要求的顶点,构建三角形,重点体会如何能不重复不遗漏地将完整的方案展现出来。在课的延伸拓展部分,教师再设一问——“构造的不同的三角形一共有多少个?”掀起一个新的思考高潮,引导学生从另一个角度去思考问题,用排列组合的方法求出符合要求的三角形个数。有序枚举的方法和组合排列的方法既可以说是不同的思维方法,又可以相互解释(排列组合是对有序枚举的进一步概括),为学有余力的学生提供了研究空间。
看似一道普通的求三角形面积的练习题,其思维训练的内涵却很广泛。教师以题目为载体,鼓励学生自主探究、合作交流,充分体验分类、转化、有序、抽象等思想方法在具体情境中的应用,大大提升了学生的学习品质和思维品质。

