基于学生学习起点培养数据分析观念
——《平均数》教学思考与实践
范立军
【课前思考】
回顾“平均数”的教学历史,一个最大的变化是:原本作为应用题范畴的求平均数,现已划入统计内容,要作为统计概念来进行教学。《数学课程标准(2011版)》明确指出:统计的核心是数据分析。这就决定了“平均数”的教学目标,应从过去注重平均数的求法,强调数量关系以及算法的多样化,转变为丰富和深化对平均数意义的理解,并让学生在收集、整理、分析数据的过程中,感受到平均数可以反映一组数据的整体水平,具有一定的代表意义,培养学生的数据分析观念。
【教学过程】
一、问题驱动,理解平均数的概念
1.情境引入。
师:从这两张统计图中,你了解到哪些情况?
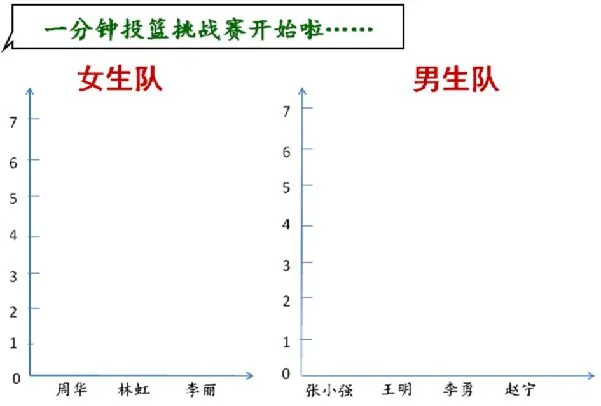
生:女生队3人参加比赛,男生队4人参加比赛。
师:男生队首先出场的是张小强,我们一起来看一下他的投篮情况。(在统计图中动态显示张小强投进了5个球)
师:张小强投进5个球后,听到“女生队3人,平均每人投进4个”的消息。张小强很高兴,因为他觉得:“我的成绩超过了女生队的任何一个人”。
师:你们觉得张小强的这句话对吗?
师:对还是不对,别忙着下结论。接下去请你把你认为的女生队的投篮情况涂在这张统计图中,来证明张小强这句话的正误。
2.意义理解。
生:我这里表示女生队的每个队员都投进了4个。这样整个女生队也是平均每人投进了4个。(如图1)
师:如果女生队是这种投篮情况的话,那张小强的话是对的还是错的?
生:对的。
生:我表示的女生队的投篮情况是周华投进了3个,林虹投进了6个,李丽投进了3个。(如图2)
师:怎么让人看明白女生队是“平均每人投进了4个”?
生:把林虹最上面的两个,一个给周华,另一个给李丽,这样就可以看到平均每人投进了4个。
生:我表示的女生队的投篮情况是周华投进了2个,林虹投进了8个,李丽投进了2个。让林虹拿出4个,2个给周华,另2个给李丽。这样女生队就平均每人投进4个了。(如图3)
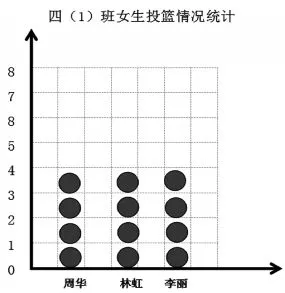
图1

图2

图3
师:我们来看看这后面两种投篮情况有什么共同点?
生:都投进了12个。虽然每人投进的球数不同,但平均以后都是4个。
生:都是投进多的同学把篮球分给投进少的同学,最后大家一样多。
师:在数学上,把这样将多出来的部分移补给少的部分,最后得到一样多的方法叫“移多补少”(板书)。而通过移多补少后得到一样多的那个数叫整组数的平均数。
(板书:平均数)
师:谁能说说在投影中的三幅图中,“4”是哪几个数的平均数?(学生回答略)
师:平均数“4”代表了周华、林虹和李丽每人都投进4个吗?
生:不是。
师:那这个“4”代表是的谁的水平?
生:代表的是女生队的整体水平。
师:是的。平均数就是代表一组数据的整体水平。
(板书:整体水平)
师:通过刚才的学习,我们可以确定张小强的这句话是错的。那么张小强应该怎么说就对了呢?
生:张小强的成绩超过了女生队的平均水平。
3.深层解读。
师:男生队的平均投篮数是多少呢?我们一起来看一下。

师:你是如何求出男生队的投篮平均数的?
生:平均数就是大家整体平均下来是多少个,所以我这样算:(5+7+2+6)÷4=5(个)。
师:“ 5+7+2+6”在求什么?“4”表示什么?“5”又表示什么?
生:“ 5+7+2+6”在求男生队投进的篮球的总数,“4”表示男生队的人数,“5”表示男生队投篮的平均数。
师:也就是说,平均数可以用“总数÷人数”来得到。我们把这种求平均数的方法叫“求和均分”。
(板书:求和均分)
生:平均数就是“移多补少”以后整体平均在什么水平。男生队最高是7个,最少是2个,另外2人分别投了5个和6个,我估计平均数大概在4个或者5个。如果是4个,多出的有3+1+2=6(个),缺少的只有4-2=2(个),不对。如果是5个,多出2+1+0=3(个),缺少的也是5-2=3(个),正好。平均数是 5。


师:整体观察数据,用“移多补少”的方法来验证平均数。
师:现在我们知道了男生队的平均投篮数是5个,比女生队高一点。看到这个情况,第五个男同学陈雷也想来参加比赛了。同学们想一下,陈雷要投进几个,才能使男生队的投篮平均数保持在5个?
生:陈雷也要投进5个球。
师:有道理。但是一分钟以后,陈雷却出现了一个不开心的表情,这说明了什么?
生:说明陈雷一个球也没有投进。
师:如果陈雷一个球也没有投进,那这时候男生队的投篮平均数是多少?
生:(5+7+2+6)÷5=4(个),“5”代表人数,“4”表示这时候的投篮平均数。
师:如果陈雷是个投篮高手,他要投进几个球才能使男生队的投篮平均数变成6个呢?
生:5×6-20=10(个),如果平均数是6个,全队5人,需要投进30个球,再减去另外4个队员已投进的20个球,就算出了陈雷需要投进10个球。
生:还用“移多补少”的思路想。平均数是6个,现在多出的是7-6=1(个),缺少的是0+1+4=5(个),总体情况是缺少了5-1=4(个)。所以陈雷再投就要去补这4个,6+4=10(个)。
师:看来现在的平均数和陈雷的投篮数密切相关。陈雷投进得多,整个队的平均数就会提高。陈雷投进得少,整个队的平均数就会下降。其实不仅仅是陈雷,队中任何一个投篮数量,都会直接影响整个队的平均成绩。平均数就是这样一个数,组中任何数据变化,都会使它发生变化。
4.跟进练习。
师:要衡量一个人的篮球水平,除了要考虑他的投篮水平,身高也是一个很重要的因素。我们一起来看看男生队4个队员的身高情况。

师:你估计这4个同学的平均身高大约是多少?为什么?
生:我估计大约是140厘米。因为这4个人中有比140厘米高的,也有比140厘米矮的。
师:平均数一定在最大和最小数据之间,有道理。那么到底是多少呢?请同学们用自己喜欢的方法来求一下。
生:(141+136+145+142)÷4=141cm。
师:大家有没有发现,这里哪位同学的身高比较特殊?
生:我觉得张小强的身高比较特殊,因为他的身高刚好和平均身高相同。
师:那你们觉得“张小强身高141cm”和“平均身高141cm”这两个“141”相同吗?
生:不相同,“张小强身高141cm”指的是张小强一个人的身高水平;而“平均身高141cm”指的是这4个同学的整体身高水平,其中有不到141cm的同学,也有超过141cm的同学。
二、数据分析,培养学生的统计意识
师:现在我们知道了张小强的身高刚好等于篮球队男生的平均身高。那么张小强的身高在全班男生中属于什么水平呢?是高的、一般的还是矮的呢?
(学生讨论交流:高的、矮的、一般的、不确定)
师:我们来看一看他们班20个男生的身高情况。

身高(cm)145 146 143 147 141 145 135 138 131 145 139 143 140 146 145 145 144 144 138 142
师:从这张统计表中,你能判断张小强的身高水平吗?
生:数据比较多,好像比较困难。
师:给同学们一点提示吧(课件圈出最高身高和最矮身高)。通过这两个数据,对你判断张小强的身高有没有帮助?
生:把表格中的身高按从高到矮排一下,就知道了。
师:那我们就来看看这20位同学的身高从高到矮排列后的情况。

147 146 146 145 145 145 145 144 144 144 143 143 142 141 140 139 138 138 135 131
师:现在能判断出张小强在班中的身高情况了吗?为什么?
生:能判断了。张小强的身高排在第14位,属于比较矮的。
师:那比平均身高矮多少呢?我们可以怎么办?
生:求出这20个男同学的平均身高,然后进行比较。
师:可以怎么求出这20个男同学的平均身高?
生:先把这20个身高加起来,然后再除以20,就能算出平均身高了。
师:好,我们请计算机帮忙算一下平均数,最后我们得到了这20个同学的平均身高是“142.2cm”,但这20个同学中没有这样的身高呀!这是怎么回事?
生:因为平均数代表的是这20个同学的整体身高水平,并不是指某一个同学的身高。
生:是把所有的同学身高平均下来,整体是142.2cm。
师:同学们回想一下,我们是经过怎样的过程知道了张小强是偏矮的?偏矮了多少呢?
生:刚才我们通过排列知道了张小强的身高处在全班男生的中间以下的水平,又通过计算得出20个男生的平均身高,知道他比平均身高矮1cm多。
师:排列可以,算平均数可以,将来我们还会有更多的办法来分析一组数据,得出一些有用的结论。
三、联系生活,体会平均数的应用
杭州西湖景区游客统计表
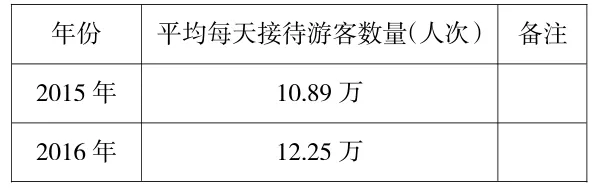
年份 平均每天接待游客数量(人次) 备注2015年 10.89万2016年 12.25万
师:你能用平均数的知识来分析这两年平均游客数量吗?
生:“2015年西湖景区平均每天接待游客10.89万人次”,说明这一年并不是每天都是10.89万人次游客,有些日子接待人数比这个数据多,有些日子接待得少。2016年也是同样道理。
生:从这里我们知道了2016年平均每天的游客数比2015年要多。但并不是说2016年任何一天都比2015年要多,也可能某一天的游客数比不上2015年。
【编辑点评】
范老师这节课的主要特色是强调“平均数”作为统计概念,即:1.强调概念的理解,而非平均数的求取;2.将平均数置于数据分析的情境之中,强调平均数的统计意义,重在发展数据分析观念。
全课的情境设计颇为丰富和巧妙。
投篮情境的教学顺序别出心裁。基于对学生学习起点的判断,从逆向问题“已知女生投篮平均数,设想女生各人投篮情况”开始,既沟通了“平均数”和“平均的数”之间的联系,又突出了二者的区别,很好地体现了尊重学生的经验、利用学生的经验、提升学生的经验。同时,在这一案例中,学生已初步体会到平均数的特点:同一个平均数可能对应不同的数据组(数据的离散程度不同),但整组数据平均下来(移多补少)正好集中在平均数上。在女生投篮案例的基础上,正向求取4个男生的投篮平均数,基于概念建构算法——求和平均、移多补少。教学之意,不在算法,而在概念的理解和应用,因此教师未在算法层面停留、跟进,而是进一步变式,引导学生思考增加一个男生后可能引起的平均数的变化,强化感知平均数的重要性质:1.单个数据对于平均数的影响;2.一组数据之于平均数的离差和等于0。
“身高”情境不是对于投篮情境简单重复,它进一步放大了“平均数”的统计背景。使学生更为完整地经历统计解决问题的全过程:要有理有据地回答“张小强的身高在全班男生中处于什么水平”,首先需要收集全班男生的身高数据,有了数据以后,可以做不同角度的加工、分析和解读,此处不仅强化了平均数作为集中量的意义,而且为中位数等知识的引进预留了空间。在这样的过程中,学生充分体会到数据承载着信息,对数据的合理处理能够带来合情的判断和推测,有效地培养了数据分析观念。
最后是对一些常见统计信息的解读。如果说前面的生活情境更多地服务于“平均数”这个数学概念的教学,那么这里是运用“平均数”概念来解读和辨析生活情境,很好地体现了素养取向的数学教学观。学生对于生活信息相对深入的反思和解释,不仅体现了他们数学素养的提高,也可视为一种公民素养的养成。

