“讲道理”数学课堂的核心
——引导学生自主建构知识
江绍权
随着课程改革的不断深入,罗鸣亮老师提出的“做一个讲道理的数学老师”的观念得到了越来越多教师的认可,这种观念也逐渐渗透到了教师的教学理念中。近年来,很多学校开展教研课,执教者、指导者和评课者都会从这节课是否呈现知识的来龙去脉,是否为数学知识讲道理的观念去设计、指导和评析。下面笔者以罗鸣亮老师的《平行四边形和梯形》这节课为例,谈谈如何引导学生自主建构新知。
一、抓住知识的生长点,引领学生自主建构
新知不是独立成一章,新旧知识必然存在联系与衔接,教师应充分把握教材中新旧知识间的联系,并帮助学生抓住这一牢固的“生长点”,通过教师搭起的“桥梁”,引领学生自主建构,逐渐同化新知。如罗鸣亮老师的《平行四边形和梯形》这节课,罗老师是这样搭起“引桥”的。在课始阶段,罗老师先出示一个信封并贴在黑板上,信封上面写着四边形,然后故意透露一些信息,从信封里露出一个直角梯形。如下图:
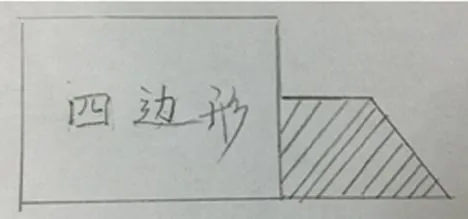
罗老师让学生猜一猜这个图形可能是什么。学生猜测是平行四边形和梯形的居多,不规则图形的较少。罗老师故意不揭示答案,吊足学生胃口,接着才出示8个图形,让学生自主交流分类。

生:1、3、6是平行四边形,2、4、5、7、8是梯形。
课堂上出现错误的资源,也是课堂精彩的一笔,许多上公开课的教师很珍惜这样的资源。对于平行四边形边的特点,学生原有的生活认识与数学教材概念的描述是很接近的,缺少的只是学科语言的提炼。而对于梯形的认识,学生脑子里只有模糊的形象,还没能完全把握它的特征。这也是教师在上课前必须对学生学情的掌握,抓住学生这个认知的生成点让学生自主去建构,把知识的理说清。罗老师针对这个学生的错误进行了引导:“你的意思是这5个都是梯形,大家同意吗?”有一学生反驳:“5号和8号图形不是梯形,是不规则图形。因为梯形的上、下两条边是互相平行的。”教师请他到黑板前做手势示范,将学生注意点引导到关注边上来,然后教师做手势引导学生想象:5号上下两条边无限延长会相交。接着罗老师拿出2号图形让学生通过交流初步建构了上下两组对比平行的四边形是梯形的不完善概念。层层递进,罗老师又拿出图形7将它旋转90度,使左右两边平行。不断变化位置后提问:为什么都是梯形?并出示1号、3号、6号图形与它比较,让学生在8个图形的辨析中感悟梯形与平行四边形、不规则四边形的不同,突出梯形一组对边平行的属性。学生初步感知了这一特征后,通过变式,突破了原有的对梯形的认识,将其上升为“只有一组对边平行”的数学概念专业化的表达。
生活中处处有数学,许多几何图形概念,学生在生活中有所感知,罗老师课前做好充足的学情调查分析,抓住学生的知识生成点,在“猜”上面做足了文章,巧设“桥梁”让学生自主交流,新旧知识相互发生作用,促使学生借助同化和顺应产生了知识迁移,将平行四边形和梯形的新的知识纳入原有的认知系统,从而引领学生从生活经验向数学经验转化。
二、抓住知识的沟通点,引领学生主动建构
《平行四边形和梯形》这节课,要让学生理清平行四边形与长方形的关系是难点。根据五年级学生几何思维的发展特点,让学生一下子接受长方形也是平行四边形,真的是思维上的一大跨越!如:在《平行四边形和梯形》这节课上,罗老师为突破这个教学难点,故意制造知识上的冲突,引导学生去发现知识间的有效连接点。罗老师还是出示一个信封,故作神秘地说:“信封里还有一个四边形,猜对的也可以送给你,可是看不见,你们能猜出来吗?需要提示吗?你们最需要什么提示?”学生要求老师提示几组平行线,罗老师却要求学生回答:“这个提示好不好?好在哪里?”这个问题设计使学生再次甄别了平行四边形、梯形和不规则四边形的区别:两组对边平行就是平行四边形,只有一组就是梯形。没有对边平行是不规则四边形。接着罗老师故意自行打开信封偷窥一眼,说:“有两组平行线。”有一学生迫不及待地喊出:“一定是平行四边形。”这个时候罗老师抽出信封里的四边形,当场蒙住了全班同学,因为罗老师抽出来居然是长方形。神奇的罗老师此时却不加以解释,话锋一转:“我能把这个长方形送给回答问题的这个同学吗?”这一问题如一石激起千层浪,学生自主交流,出现了不同的声音。正因为罗老师引导学生抓住知识间的连接点,最后由一个女生一锤定音:“因为平行四边形有两组平行线,长方形也有两组平行线,长方形是一个特殊的平行四边形。”听课席响起雷鸣般的掌声。罗老师故作“呆萌”问:“老师们为什么要给她鼓掌?”生:“她把平行四边形的特征(两组对边平行)说出来了。”教师乘机追问:“如果通知所有的平行四边形来开会,它要不要来?它特殊在哪里?”
当教师给出两组对边平行这个信息后,学生根据边的特征马上想到了平行四边形,而教师拿出的却是长方形,正是教师在长方形和平行四边形知识之间设置沟通点——两组对边分别平行,学生的思维迸发出火花,把注意力聚焦于边的特征,在师与生、生与生的争论中达成一致。
三、抓住知识的运用点,引领学生拓展建构
一节活跃的课堂,不能光看课堂表面热闹,更重要的是看学生思维的活跃程度。要使学生思维活跃,教师不能进行“填鸭式”的训练,必须放手,在实践运用中,设计的练习要抓住知识的运用点,让学生自主拓展建构,让学生掌握的新知越来越完善。
《平行四边形和梯形》这节课练习环节的设计别具一格,罗老师出示他女儿给他的信封,还是让学生猜信封里的四边形是什么图形,“长方形、正方形、平行四边形、梯形”,学生的答案不一,当学生一致认为不知是什么样的四边形时,罗老师却抽出来是一个直角三角形并将它贴在黑板上。
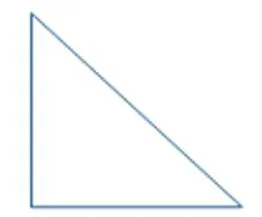
罗老师解释他的女儿为了让他方便携带,故意把这一个四边形剪分成了两个图形。接着罗老师又从信封里拉出一个直角梯形。
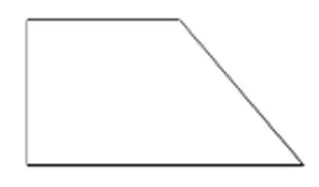
罗老师故意设疑:“咦!我女儿到底把什么图形剪成这样子?”“长方形、平行四边形、梯形、三角形……”学生众说纷纭。于是罗老师请这些学生逐一上台利用剪后的三角形和梯形把原图拼了出来。

本环节,罗老师仅用一个道具——一个标有四边形的信封就贯穿课的全程,要学习的知识有如信封中的图形半遮半露,这露出来的一部分恰是学生的已有知识,教师巧妙地将学生的思维引领到学习的关键点,而随着学生的自主建构,那被信封遮住的部分——新知,也犹如洋葱一样被片片剥开,深深地纳入到学生原有的知识结构中。

