让“学”与“教”自然对称——《图形的运动——轴对称》教学设计（一）

严红兴

【教学过程】

一、反馈导学单，整体感知轴对称图形

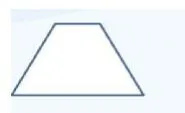
图1

图2

首先让我们来看看同学们导学单完成的情况。

1.图1是轴对称图形吗？它的对称轴在哪里？谁来指一指？

2.图2的对称轴在哪里？你能指出来吗？还有不同的吗？

预设：我们发现同一个轴对称图形可以有多条不同的对称轴。

3.你觉得图3这个轴对称图形的另一半可以画在哪里？

预设：沿着四条不同的对称轴进行对称。

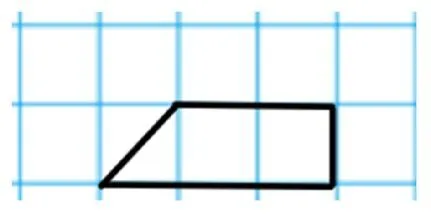
图3

呈现：你有办法验证图4、5、6的轴对称图形吗？

图4

图5

图6

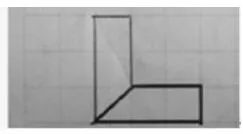
图7

预设：请你想象沿着对称轴对折一次。（课件操作动画链接验证）

4.图7的对称轴在哪里？指明画出的另一半在哪里？

验证：沿着这条对称轴对称过去，它们能重合吗？（操作动画链接验证）

归纳：观察四组对称图形有什么相同？有什么不同？

预设：选择不同的对称轴，画出来的图形位置就不一样。

板书：形状大小不变、位置变化。

过渡：从导学单中，老师还了解到同学们还有一些问题：

【设计意图：前测中，我们发现大部分学生已经能够找到简单图形的对称轴，对于有多条对称轴的图形找对称轴，还存在一定的遗漏情况。通过这一组题的反馈，激发学生原有经验，丰富了学生对于轴对称图形的表象。】

二、下对称棋，逐步探究对称点的特征

1.下对称棋，探索对称点到对称轴的距离相等。

过渡：下面就让我们借助“对称棋”游戏来研究“对称点的连线和对称轴之间的联系”。

教师示范一组A、A'，继续在对称轴左边下好一颗B，接下来该怎么下呢？

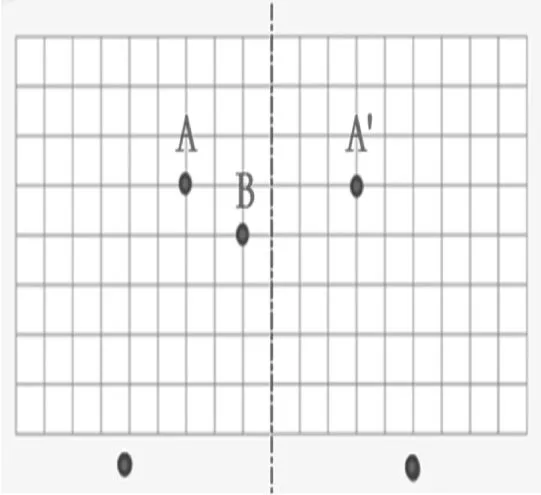
预设：学生在对称轴右边指出B点的对应点，并阐述自己的想法。

点拨：如果现在老师继续下一颗C，你能下出关于它的对称棋吗？

2.连接对称点成轴对称图。

连点成形：现在，老师把左右两边的对称点都连起来。猜猜是一个什么图形？

观察归纳：仔细观察这两个对称的三角形，有什么发现？

预设：两个三角形对应的顶点到对称轴的距离相等。

验证：你能从三角形中任意找一点来验证这个结论吗？

预设：从三角形中任意找出一对对称点连接验证。

小结：刚才同学们通过下对称棋又发现了一个特征，即轴对称图形中的所有对称点到对称轴的距离相等，并且它们之间的连线与对称轴垂直。

【设计意图：通过下对称棋寓教于乐，自主发现对称点与对称轴的关系，连点成面后形成三角形，在寓教于乐的游戏过程中发现轴对称图形的特征。】

三、利用对称点的关系画出三角形的轴对称图形，理解轴对称图形的本质

1.画三角形的轴对称图形。

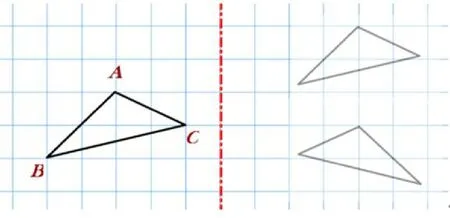
直观想象：现在再给你一个三角形，你能画出它的轴对称图形吗？

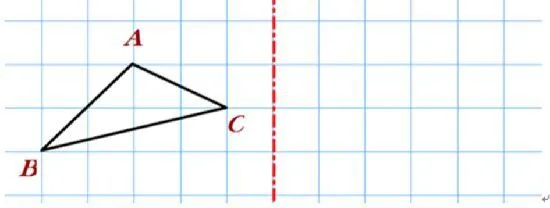
预设：想象、辨析、判断、说理。

点拨：准确的三角形到底在哪里？具体是怎么样的？请你运用刚才发现的轴对称图形的特点，自己动笔在纸上画一画。

预设：在方格纸上独立尝试画出轴对称后的三角形。

介入：（教师巡视观察）如果有困难，可以打开平板里画三角形的视频来自学；如果画好了，也可以对照平板视频验证自己画的三角形是否正确。

反馈错例，总结画法：

（1）呈现：（对称点距离数错画成平移变换的和没有标对应点的）请仔细观察以上几幅作品，你有什么想说的？

（2）我们应该怎样画出一个正确的轴对称图形？

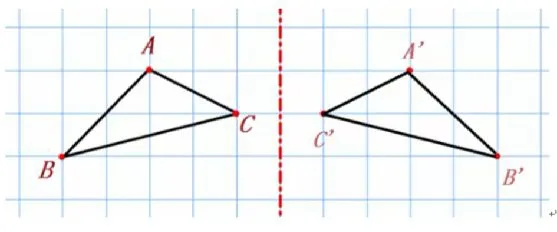
预设：先画图形的对应点，然后连接各个对应点。

2.变换位置画图形，深入理解轴对称图形的特征。

变式：

（1）如果把原来的三角形往左移动，它的轴对称图形会怎么变化？（边说边用白板移动）

（2）把原来的三角形往右移动呢？C点的对称点又在哪里？

（3）如果三角形不动，把对称轴进行平移或旋转，你还能画出三角形的轴对称图形吗？

预设：借助三角板独立画图。

教师巡视，收集典型的错误作品并反馈，进行归纳总结。

讨论：为什么对称点到对称轴的连线要画上直角符号？这条线是用来做什么的？

预设：因为它们的连线和对称轴垂直，借助对称点到对称轴的距离相等可以画出对应点。

【设计意图：通过画出三角形的轴对称图形，巩固轴对称图形的特征；在多次变换的过程中进一步理解轴对称图形的内在关系；尤其是在对称轴旋转后，由水平方向对称变成了非水平方向对称，提升了空间想象的要求，促使学生运用轴对称变换的本质属性解决问题。】

四、设计应用，体会价值

1.判断下列图形是否为轴对称图形，如是请画出对称轴。

预设：针对误选的平行四边形，运用轴对称图形的特征讨论纠错，结合判断过程课件动态演示。

2.运用轴对称变换设计图案。

预设：根据所选图形，运用轴对称变换，独立设计出密铺及类似图形并小组交流。

反馈欣赏：展示基本图形变换出美丽图案的过程，拓展到实际生活中的轴对称应用。

【设计意图：通过对简单平面图形的判断，让学生认识到一般平行四边形是非轴对称图形。用简单的平面图形借助轴对称变换设计出新的图案，感受轴对称变换的应用价值。】

五、课堂小结，回顾感悟

回顾整理：对照课前的疑问，你的问题都解决了吗？

【设计意图：在回顾与反思中整理全课内容，回应课前学生提出的疑惑。】