大型船舶轴系回旋振动特性的模拟计算及实测

周飞云

(中国船级社 福州分社，福州 350008)

船舶推进轴系振动通常有扭转振动、纵向振动和回旋振动等3种形式。20世纪中叶，美国“自由”轮因推进轴系回旋振动导致螺旋桨轴锥部大端龟裂折损，造成螺旋桨掉入海中，引起人们对推进轴系回旋振动的关注；随后Panagopulos和Jasper提出轴系回旋振动共振现象，并给出轴系固有频率计算Panagopulos和Jasper简化公式。[1]

根据《钢质海船入级规范》[2]的要求，除了安装具有人字架和万向轴的推进轴系的船舶须进行轴系回旋振动计算之外，其他船舶在设计和建造过程中通常不考虑轴系回旋振动对轴系安全性的影响。对于一些大型船舶，尤其是配备大型4叶片以上螺旋桨的船舶，其轴系较长，且没有艉管前轴承或中间轴承，造成整个轴系的弯曲刚度下降；而螺旋桨在不均匀的伴流场中工作时将产生周期性的弯曲力矩作用在螺旋桨轴上，当螺旋桨叶片的共振频率落在推进轴系正常转速范围内时，大规格多叶片螺旋桨的自激频率与轴系的固有回旋振动频率接近，导致推进轴系产生强烈的回旋共振，从而造成艉管后轴承过热或早期过度磨损，并导致轴承套腐蚀、艉管密封装置漏损及螺旋桨轴锥端前面键槽区域内产生附加交变弯曲应力，甚至出现龟裂、折断等疲劳破坏；此外，严重的轴系回旋振动导致轴承反力的动力被放大，进而引起艉部结构的振动，而过度的船体结构振动除对人员的舒适性产生影响之外，还可能引起局部结构疲劳损坏或机械设备故障，甚至影响船舶的安全航行。[3]

轴系回旋振动的理论计算一般采用传递矩阵法，由于其表达式简单、易于编程，这里采用传递矩阵法对某船的推进轴系回旋振动进行建模分析。回转振动测量通常通过转速扫描发现共振，若共振点在正常转速范围之外，则认为不存在共振问题，这种测量方式存在准确度不高、误差较大的问题，不能进行定量分析[4]，这里通过使用非接触式的电涡流位移传感器，选用瓦锡兰公司的轴系振动分析仪，对推进轴系的回旋振动情况进行更为精确的测量分析。

1 传递矩阵法回旋振动计算分析

推进轴系的回旋振动是在悬臂端带有螺旋桨的多点支承转轴的进动运动，推进轴系在水平面和垂直面上的投影见图1。螺旋桨和转轴在以角速度ωs绕其自身的几何轴线旋转的同时，该轴线以角速度ωn绕Ox轴旋转[5]。前一种旋转相当于自转，后一种旋转相当于公转，公转角速度ωn又称进动角速度或回旋角速度。转轴上任意截面的绝对角速度ω等于自转角速度ωs与回旋角速度ωn的矢量和，转轴上任意截面的绝对角速度可近似表示为

ω=ωs+ωn

(1)

当回旋角速度ωn的方向与自转角速度ωs的方向相同时，称为正回旋，反之称为逆回旋(见图2)。

a) 轴系 b) 水平面投影 c)垂直面投影

图1 轴系在水平面和垂直面的投影

a) 正回旋 b) 逆回旋

图2 轴系正回旋和逆回旋

回旋振动模型将螺旋桨简化为均质薄圆盘，其质量和转动惯量已包含附连水作用，转轴简化为无质量弹性轴，忽略阻尼的作用，回旋振动的频率方程为

(2)

式(2)中：Jp和Jd为分别为螺旋桨的极转动惯量与径向转动惯量，kg·m2；ω为螺旋桨的旋转角速度，rad/s；θz和θy为螺旋桨中心处轴在计算x-y平面及x-z平面的转角，rad；m为螺旋桨(包含附连水作用)的质量，kg；δw为螺旋桨处受到单位力作用时，其几何中心处产生的挠度，m/N；Φw为螺旋桨处受到单位力作用时，其几何中心处产生的轴的转角，rad/N；δM为螺旋桨处受到单位力矩作用时，其几何中心处产生的挠度，m/N；ΦM为螺旋桨处受到单位力矩作用时，其几何中心处产生的轴的转角，rad/N；ωn为回旋振动频率，rad/s。

当轴不旋转时，ω=0 ，式(2)即为轴系回旋振动频率方程，由此求得的ωn就是轴系回旋振动固有频率。

某船为近海航区大型集装箱船，主机选用宁波中策动力四冲程柴油机，螺旋桨选用5叶桨(参数见表1)，主机输出经弹性联轴节、减速齿轮箱、中间轴及艉轴驱动定距螺旋桨(参数见表2)，轴系布置见图3，整个轴系以艉管后轴承、艉管前轴承及齿轮箱大齿轮轴承等3道轴承作为支撑。

表1 螺旋桨参数

表2 主机参数

由图3可知，整个推进轴系以艉管后轴承、艉管前轴承和齿轮箱大齿轮轴承等3道轴承作为支撑点，在计算模型中简化为弹簧支点，各支撑点刚度数据见表3。

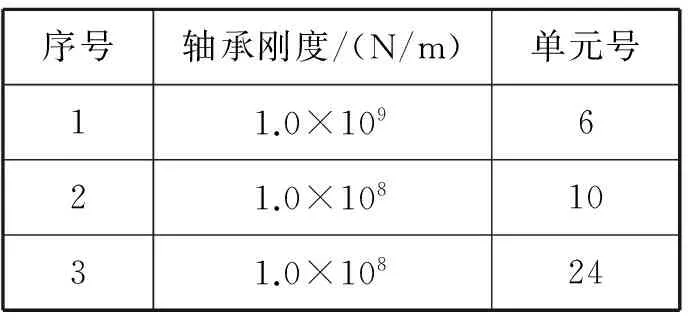
序号轴承刚度/(N/m)单元号11.0×109621.0×1081031.0×10824

采用传递矩阵进行轴系回旋振动计算，一般采用集总元件与分布参数元件相结合的简化模型(见图4)，螺旋桨简化为均质刚性圆盘元件，其质量与转动惯量作为集总参数，螺旋桨轴、艉管轴和中间轴自然分段为等截面均质轴段元件。为清晰地绘制振动模型曲线，可对轴段元件进行适当细分，一般可忽略轴段回旋效应及剪力和轴向推力的影响，若法兰连接的弯曲刚度与轴相比大得多，则可不考虑其弯曲变形，直接将2个连接法兰作为均质刚性圆盘元件，轴段元件支撑刚度常用等效弹簧处理，艉管后轴承刚度一般为1×109～3×109N/m；在回旋振动计算分析中，将轴承简化为点支撑，对于中间轴承和艉管前轴承，可认为支反力沿轴向均匀分布，支撑点在轴承中点位置。[6]对于艉管后轴承，由于悬臂端螺旋桨的作用，支撑反力沿轴承长度的分布很不均匀，支撑反力合力的作用点偏向艉端，并受轴承磨损程度、船舶负载和船体变形等因素的影响。在进行回旋振动计算时，对于白合金艉管后轴承，支点与轴承衬后端面之间的距离一般取轴承衬长度的1/7～1/3。[7]表4为该船主推进轴系主支数据，6单元、10单元及24单元为轴承支点位置。

轴系艉端螺旋桨的边界为自由端，艏端边界条件按其艏端元件为飞轮、齿轮箱大齿轮或高弹联轴节分别取为固定端、铰支端或自由端。螺旋桨附水有质量和转动惯量2个作用，比较精确的值可由理论公式计算得到，初估时可用附加系数表示：质量附水系数为1.10～1.30；极转动惯量附水系数为1.25～1.30；径转动惯量附水系数为1.50～2.00。在计算中：质量附水系数取1.26；极转动惯量附水系数取1.28；径转动惯量附水系数取1.8。[8]

表4 推进轴系模型主支数据 mm

经计算，1次正回旋共振转速为572.97 r/min，叶片次正向回旋共振转速为97.17 r/min；根据表3，螺旋桨轴额定转速为102 r/min，1次正回旋共振转速不大于额定转速的20%，不会出现共振，满足《钢质海船入级规范》的要求。叶片次正向回旋共振转速为97.17 r/min，叶片次正回旋共振转速落在螺旋桨轴额定转速的0.85～1.00范围内，产生回旋振动共振点，计算结果见表5。

表5 回旋振动计算结果

2 推进轴系回旋振动测量

2.1 回旋振动测量基本原理

选用电涡流位移传感器[9]对轴系回旋振动进行测量，该传感器能非接触、高线性度及高分辨率地静态和动态测量被测金属导体距探头表面的距离，是一种非接触的线性化计量工具。电涡流传感器能准确测量被测体探头端面之间静态和动态的相对位移变化，其基本原理是根据法拉第电磁感应原理，当将块状金属导体置于变化的磁场中或将其放置在磁场中作切割磁力线运动时，导体内将产生呈涡旋状的感应电流，该电流称为电涡流，该现象称为电涡流效应。

回旋振动测量基本原理图见图5，电涡流位移传感器通过检测轴在运转过程中的横向位移，将模拟信号(位移)通过A/D转换器转换为数字信号(电压或电流信号)，回旋振动分析仪收到该信号后根据预设的回旋振动分析程序进行分析计算，将计算结果传至上位机显示或进行打印。

2.2 回旋振动实船测量

在此次回旋振动测量所用设备中，选用中航工业航空动力机械研究所研制的TR电涡流传感器、瓦锡兰公司研制的AA8系列轴系振动分析仪(见图6)及瓦锡兰公司提供的关于轴系振动测量的上位机程序模块。由于该船的艉轴布置在艉轴隧中，布置检测传感器有困难，因此将电涡流传感器布置在中间轴上。此外，为确保测量的准确性和有效性，在中间轴长度范围共布置2套电涡流传感器，分别布置在距中间轴前法兰面1 250 mm和1 700 mm处，实际布置见图7。

此次轴系回旋振动测量在主机常用转速范围内进行，设置测量区间为主机转速150～620 r/min，螺旋桨转速25～103 r/min，最终的测量结果见图8和图9。2组传感器的测量数据显示在螺旋桨转速91 r/min和93 r/min时存在共振点，即螺旋桨转速91～93 r/min的区间内存在回旋共振现象。根据理论计算结果(如表5所示)，在螺旋桨转速为97 r/min时存在二次回旋共振，理论计算结果与实际测量结果相符。

3 结束语

通过上述对推进轴系回旋振动的计算和测量分析可知：对于大型船舶和超大型船舶，由于船体(特别是船尾)的刚度下降、轴系较长，并采用大规格多

叶片的大型螺旋桨，导致轴系的弯曲力矩增大，推进轴系回旋振动共振频率降低，螺旋桨在水中的激振频率落在轴系正常转速区间内，造成回旋共振。因此，为确保轴系安全、有效运转，对于一些长轴系大型船舶及特殊推进轴系船舶，特别是配备多叶片螺旋桨(4叶片及4叶片以上)的推进轴系的船舶，应进行必要的回旋振动计算，并建议在主机常用转速区间范围内进行轴系回旋振动的测量分析，以验证轴系校中的有效性，从而确保轴系安全、有效运转。

[1] 周海军. 推进轴系回旋振动及其支撑结构振动特性研究[D].哈尔滨：哈尔滨工程大学,2013.

[2] 中国船级社.钢质海船入级规范[S].北京:人民交通出版社,2012:1605-1606.

[3] 中国船级社.船上振动控制指南[S]. 北京：人民交通出版社，2000：102-115.

[4] 祁亮,周瑞平,崔金环. 中间轴承对船舶轴系回旋振动特性的影响[J].造船技术，2011(4)：35-38.

[5] 王建，陈建伟，闫方才，等.基于ANSYS的轴承磨损对船舶长轴系回旋振动的影响分析[J].交通科技，2016(1)：167-170.

[6] 陈锡恩,高景.船舶轴系回旋振动计算及其参数研究[J].船海工程,2001(5)：8-11.

[7] 夏极,蔡耀全,刘金林,等. 轴承油膜动力特性系数对轴系回旋振动影响[J].舰船科学技术，2016，38(1)：62-66.

[8] 张伟,吴伟亮. 基于有限元法的气垫船轴系回旋振动特性计算[J].舰船科学技术，2014(10)：37-40.

[9] 龙文学. 船舶推进轴系振动检测装置研究[D].武汉：华中科技大学，2011:34-59.