物理竞赛中使用积分法求解感应电动势一二

刘玉琴 宋善炎

(湖南师范大学物理与信息科学学院 湖南 长沙 410081)

物理竞赛中使用积分法求解感应电动势一二

刘玉琴 宋善炎

(湖南师范大学物理与信息科学学院 湖南 长沙 410081)

为提升物理竞赛中学生运用积分法解决物理问题的能力，以感应电动势的求解为例，提出了用积分法解题的一般思路.对于动生电动势，先寻找动生电动势微元，再通过对微元积分求解；对于感生电动势，在已知感生电场表达式时，先求出感生电动势微元，再对微元积分求解，也可先利用积分求出通过回路的磁通量，再根据法拉第电磁感应定律求解.

积分法 动生电动势 感生电动势

根据引起磁通量变化的原因，感应电动势有动生电动势和感生电动势之分.当磁场B不随时间变化而闭合电路的整体或局部在运动时，回路中存在动生电动势，其在数值上等于非静电力洛伦兹力移动单位正电荷所做的功；当磁场B随时间变化而闭合电路任一部分都不动时，回路中存在感生电动势，其在数值上等于非静电力感生电场力移动单位正电荷沿回路一周所做的功.若磁场B随时间变化的同时闭合电路的整体或局部也在磁场中运动，此时回路中的电动势为动生电动势和感生电动势的叠加.

对于感应电动势的计算，高中教材介绍了通过法拉第电磁感应定律进行求解的方法，求解工具为简单的初等数学知识.而在物理竞赛的一些情景中，难以通过初等数学工具求解，需要借助高等数学中的积分法进行求解，下面通过一些例题来说明积分方法的应用.

1 动生电动势的计算

在高中阶段，动生电动势的常用计算公式E=Blvsinθ，当导体上各点的速度不一样时，若各点的线速度是均匀变化的，我们可以利用平均速度来求解动生电动势，如例1.但对于非均匀变化的情况，用初等数学知识难以解决，需利用

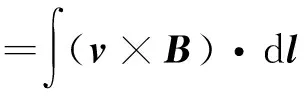
进行求解，如例2和例3.

【例1】如图1所示的金属杆AB在垂直于磁场的平面内以角速度ω绕O轴匀速转动，求A，B间的动生电动势[1].

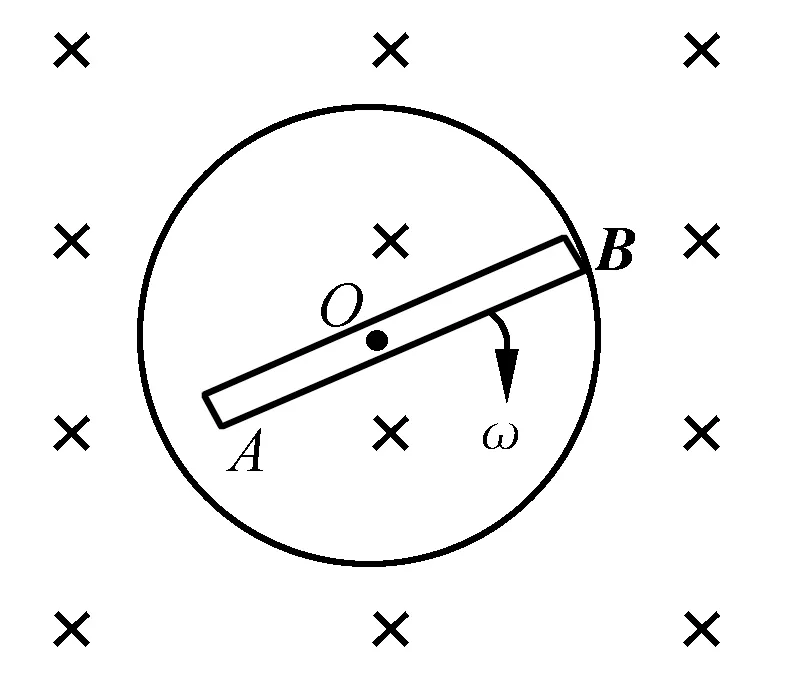
图1 例1题图

dε=(v×B)·dl=Bωldl

则

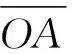
则

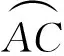
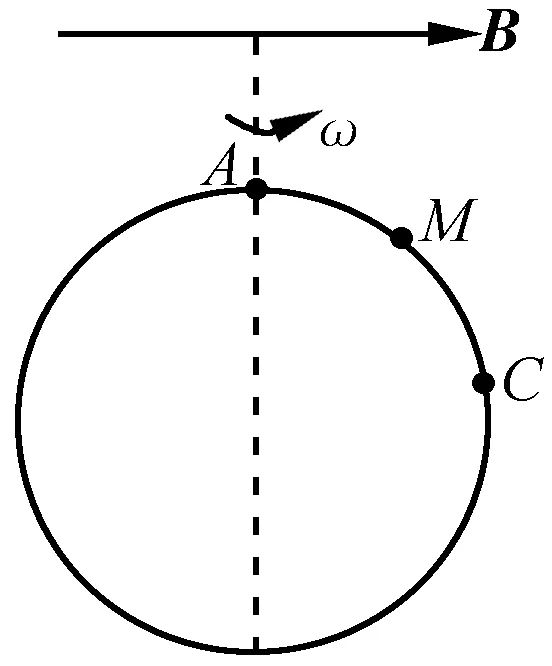
图2 例2题图

解答：取金属线圈上一微元dl，其产生的感应电动势为

dε=(v×B)·dl=Bωrdlsinα

其中

r=Rsinαdl=Rdα

则

dε=Bω(Rsinα)sinαRdα=BωR2sin2αdα

故AM上的感应电动势为

AC上的感应电动势为

此外，在有些问题中杆的运动方向、杆的轴线方向都和B不垂直，而且杆上各点的速度又不同，此时用积分的方法求解动生电动势会更简单，以例3为例进行说明.

【例3】如图3所示的直角坐标系中，有一绝缘圆锥体，半锥角为θ，轴线沿z轴方向，顶点在原点处.有一条长为l的细金属丝OP固定在圆锥体的侧面上，与圆锥体的同一条母线重合.空间存在着沿x轴正方向的匀强磁场B.试讨论当圆锥体沿如图所示方向做角速度为ω的匀角速转动时，OP上感应电动势的情况[1].

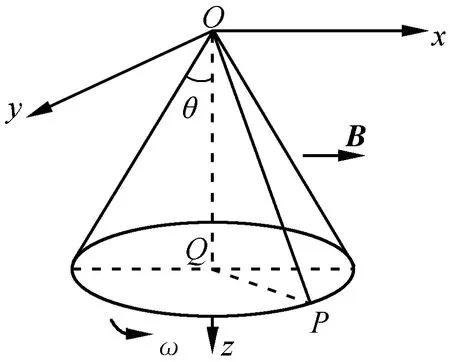
图3 例3题图

解答：由右手螺旋定则，容易判断O点和P点电势的高低.由于杆上各点的速度各不相同，杆的运动方向并不总是与B垂直，杆的轴线方向与B不垂直，因此考虑利用积分方法进行求解.

当P点的坐标x为正时，P点的电势都高于O点的电势；当P点的坐标x为负时，P点的电势都低于O点的电势.

(1)当P点的y坐标为零，即OP在xOz平面时，此时OP上的感应电动势最大.

在OP上取一微元dl，其上的动生电动势为

dε=(v×B)·dl=ωlsinθBcosθdl

则OP上动生电动势的大小为

(2)当P点运动到某一位置(图4)，P点的x和y坐标都大于零，QP与x轴的夹角为α时，在OP上取一微元dl，其上的动生电动势为

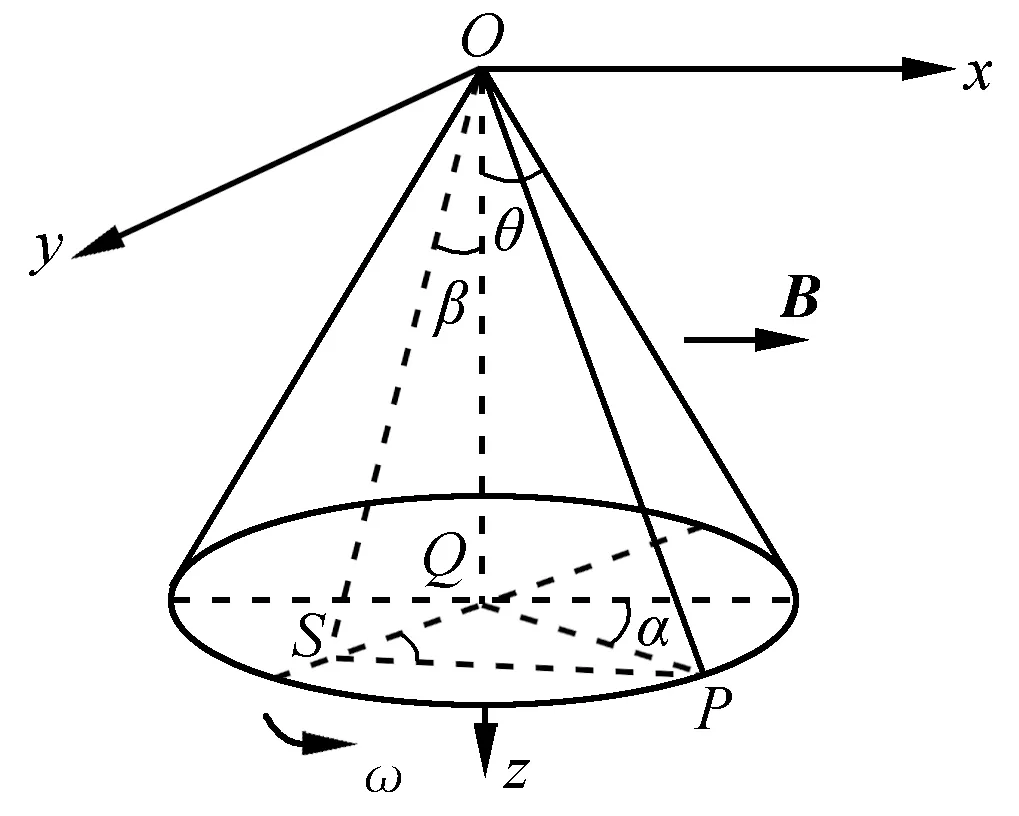
图4 情况(2)分析图

即OP上动生电动势的大小为

总之，在使用积分法求解动生电动势时，只要选取导体微元dl，将其对应的动生电动势

dε=(v×B)·dl=vBsinθcosαdl

2 感生电动势的计算

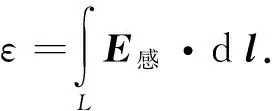
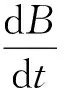
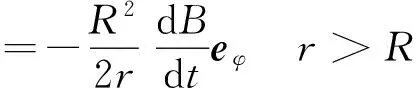
其中eφ为E感方向的单位矢量，与r垂直.

图5 无限长载流螺线管分析

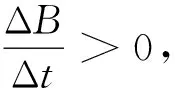
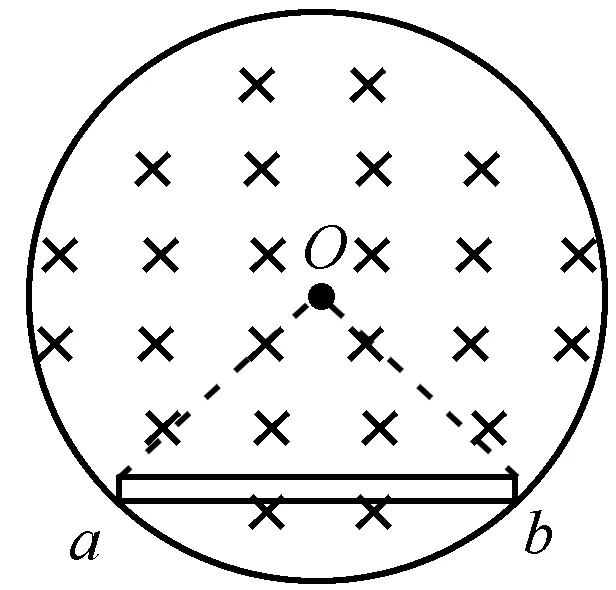
图6 例4题图

在ab上距离O点为r(0≤r≤R)处取一长度微元dl，其感应电动势为dε，则

代入相关数据

进行积分运算，有

【例5】若在例4的基础上，将导体棒ab延伸到螺线管外，并使得ab=bc=R，如图7所示，求此时导体棒ac的感应电动势εac[1].

图7 例5题图

解答：导体棒ac的ab段处于磁场区域内，bc段处于磁场区域外，其对应的感生电场的表达式不同，仍可利用积分的方法分别求出两段的感生电动势再进行求和.由例4知，对ab段

同理对bc段，有

其中ds=dlcosα,ds=rdα，则

故

顺便提一下，由于E感与r垂直，Oa,Ob,Oc段感应电动势为零，在平时的学习中，我们常常利用法拉第电磁感应定律求出回路Oab和回路Obc的感应电动势从而来求ab和bc段的感生电动势，但养成利用积分思维来解决物理问题的习惯对物理竞赛学生顺利学习力学电磁学部分的其他竞赛内容来讲非常重要，而且有利于提升学生的思维层次及问题解决能力.

【例6】如图8所示，无线长直导线载有交变电流I=I0sinωt,并与矩形线圈共面，设t=0时电流方向向上，试计算矩形线圈上的感应电动势[3].

图8 例6题图

解答：由于矩形线圈不同位置的磁场强度大小不一样，因此，在计算矩形线圈的磁通量时应采用积分的方法，再利用法拉第电磁感应定律求出感应电动势.

在距离导线x处取一面积微元，则磁通量

dΦ=B·dS=Bldx

其中

故矩形线圈的磁通量

由法拉第电磁感应定律有

1 张大同.物理竞赛教程(高三年级)(第4版).上海：华东师范大学出版社，2012.49～52

2 贾启民，郑永令，陈暨耀.电磁学(第3版).北京：高等教育出版社，2010.279

3 宋善炎.竞赛物理.长沙：湖南师范大学出版社，2013.272

刘玉琴(1992- )，女，在读硕士研究生，研究方向为课程与教学论专业.

指导教师：宋善炎(1964- )，男，博士，教授，研究方向为物理课程与教学论.

2016-10-02)