《植树问题》教学设计

韦毅菊

【教学内容】

人教版五年级上册《数学广角——植树问题》。

【教学准备】

课件、学生画图用的A4纸每人一张。

【教学过程】

一、提出问题

师：今天我们一起来讨论一类数学里面比较有趣的问题，叫做植树问题。听说过吗？请看：同学们在全长n米的小路一边植树，恰好每隔5米栽一棵，一共要栽多少棵树？

方法引导：

师：看得懂吗？谁来解释一下题目的意思？有什么困难的地方？

预设：n是多少不知道。

师：有没有跟他想法一样的？那么在不知道的情况下，你觉得可以怎么办呢？

预设：可以举例，找规律。

出示要求：

师：下面就请你自己解决问题，在解决问题时，老师有两个要求，请看：

（1）四人小组合作，可以用图示、算式、举例等方式来表示解决问题的过程，要求尽量让别人能够看得懂。

（2）问题解决后，记得把最后的结论也记录下来。

二、讨论问题

教师巡视目标：寻找正确答案（n÷5+1，n÷5，n÷5-1），对有困难的小组提示用举例的方法验证。

1.展示结论。

师：差不多了吧。刚才老师看到很多同学都在努力地思考。有的小组可能得出了答案，有的可能暂时还没有得到答案，不要紧。得到答案或者大致有方向了的举一下手。

［将学生的答案（n÷5+1，n÷5，n÷5-1）板书在黑板上］

师：同学们中出现了这几种不同的答案，现在我们还不能确定哪一种是正确的。那你们能想办法来证明自己的结论是正确的吗？我们先请第一种结论的同学来说一说。

2.讨论两端都栽的情况。（n÷5+1）

（1）请学生上黑板展示。

师：你们有什么要问他的吗？

预设：为什么用n÷5？为什么要加1？

［说明：弄清结论中的n、5、1和n÷5分别表示什么，特别指出n÷5表示的含义］

师：这组同学想到了什么办法来证明自己的结论是正确的？

预设：举例。

师：通过什么办法来使别人能够看懂？

预设：画图。

（2）展示更多学生的例子。

（3）对比求同。（投影三位学生的例子）

师：同学们，请你观察这三位同学的例子，有什么发现？

预设：算式都有+1。

师：为什么都要+1呢？

预设：因为两端都要栽，通过一一对应的方法知道，棵数比间隔数要多一。

（4）课件演示一一对应过程。

师：真棒！老师把你们的想法做成了视频。（出示微课视频）

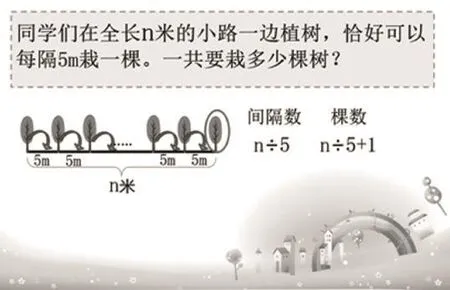
师：同学们，n米长的道路一边植树，恰好每隔5米栽一棵，我们用路的长度n除以间隔的长度5米，求出n米可以分成几个5米，也就是一共有多少个间隔，所以，在这里n÷5表示间隔数。每隔5米栽一棵，在两端都栽的情况下，通过一棵树对应一个间隔的方法，我们发现，最后还多出一棵树。所以，栽的棵数会比间隔数多1，也就是栽了（n÷5+1）棵树。同学们，你们听明白了吗？

［板书：棵数=间隔数+1，图示中圈出最后一棵树］

3.讨论一端栽一端不栽（n÷5）和两端都不栽（n÷5-1）的情况。

师：同学们非常聪明，想到了用画图和举例的方法验证了第一种答案是正确的。那么这两个答案是不是错了呢？

预设：不是。

师：请你也用同样的方法来验证。

（1）n÷5。

预设：也用举例的方式验证一端栽一端不栽的情况。

师：听明白了吗？还有谁也想说？

师：谁来把这种情况小结一下？

［课件举例演示一端出现障碍物和一一对应的过程］

（2）n÷5-1。

师：这种方案，谁来验证？

预设：通过举例的方式验证两端都不栽的情况。

师：有什么想问他的？

预设：为什么-1呢？

师：谁来把这种情况小结一下？

［课件演示两端出现障碍物和一一对应的过程］

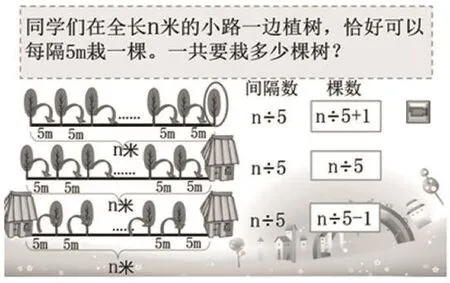
4.三种情况对比小结。

师：刚才同学们通过举例、画图等方法，把一道看似复杂的问题分析得非常清楚。观察黑板上的三种情况，你发现它们有什么共同点？

预设：都有n÷5。

师：对，为什么都要先算n÷5呢？

预设：用n÷5求出有几个间隔，根据间隔数和实际情况来确定栽的棵数。

师：又有什么不同点呢？

预设：不同点是根据实际情况不同，有些需要+1，有些不用，还有些要-1。

师：真棒，我们来试试用植树问题的知识解决生活中其他的问题。

【设计意图：自主探究、动手操作、合作交流是学生学习数学的主要方式。在这个过程中，学生会通过自己的思考举出实例。同时在举例的过程中发现植树问题有三种不同的情况，进而展开讨论，这是一个学生自主建模的过程，他们能在这一过程中体会探究的乐趣。】

三、应用模型，解决实际问题

1.在一条全长2km的街道一旁安装路灯（两端也要安装），每隔20米装一盏。一共要安装多少盏路灯？

2.把一段木头锯成等长的5段，每锯一次需要2分钟，一共需要（）分钟。

3.16名同学排成一列纵队，每2人之间相距1米，这列队伍长（）米。

【设计意图：练习是学生熟练数学知识的重要途径。通过三类实际问题，让学生在应用模型的过程中体会建模的意义。同时感悟数学与生活的密切联系，体会数学就在我们身边，生活中处处有数学，增强学生应用数学的意识。】

四、总结提升

师：同学们，今天我们学习的是植树问题，那么装路灯、锯木头、排队这些问题也是植树问题吗？都不是在植树了，还是植树问题吗？其实，我们可以把这些问题放在一起观察，大家请看，在图一中我们可以把树看成一个个的点，图二中，可以把什么看成点呢？（路灯）图三呢？

预设：这些都是点和间隔的问题。

师：对啊！同学们，其实植树问题就是在研究点和间隔的关系。［板书：点和间隔的关系］

师：生活中，你还在哪里发现有这样的关系呢？（手、走楼梯等）

【设计意图：拓展延伸，引向深入，这是本次建模的关键步骤。寻找“植树问题”的相同点，对模型进行提升，引导学生把知识点串成线，提高学习数学的灵活性。】