逆向物流网络优化及其算法设计

李姗姗

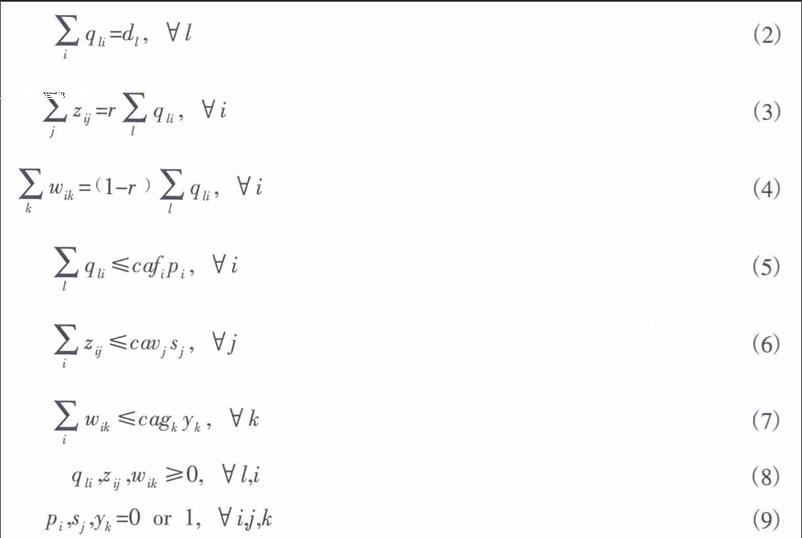
摘 要：分析了产品回收流程，指出在回收检验中心对产品进行质量检测并分类处理，有助于降低逆向物流总运营成本。针对到这一特点，结合流量平衡与生产能力等特有约束，建立了新的3阶段逆向物流网络混合整数规划模型，以确定回收检验中心、修复中心与垃圾处理中心的位置、数量与规模，以及对各网络路径上的物流流量进行分配。考虑到其NP-hard特性，开发了遗传算法，以获得大规模问题的近似解。大规模实验表明，所构建的混合整数规划模型与遗传算法是有效的，且遗传算法的求解效率与求解质量也优于LINGO软件。

关键词：质量检测；逆向物流；数学模型；最优解

中图分类号：F713.2 文献标识码：A

Abstract： Through the analysis of handling procedure for returned product， it is suggested returned products should be disposed differently after quality inspection， so as to minimize the total costs. Considering the flow balance capacity limit and capacity limit constraints， a new mixed integer programming model for three-stage reverse logistics network is proposed， in order to obtain the quantity of various infrastructures， the scales and locations. Because it is NP-hard， a genetic algorithm is proposed. Random experiments show that the algorithm and model are effective. Meanwhile， when the experiments are larger， the genetic algorithm outperforms LINGO software on solving efficiency.

Key words： quality inspection； reverse logistics； mathematics model； optimal solution

0 引 言

物流网络设计是供应链管理的一项重要内容，其以确定网络中的设施数量、位置与规模，以及各类设施间的合理物流量为主要目的。由于在較短时间内很难改变一个现有设施的位置与规模，且需要付出较大的成本代价，因此物流网络设计是一项战略性决策，对其进行优化的回报要远远大于其它战术性与作业性决策问题。近年来，关于物流网络设计的研究层出不穷，大致可分为三类：一是从正向角度进行优化[1-3]；二是从逆向角度进行研究；三是对正向物流网络与逆向物流网络的整合性研究[4-5]。本文主要是面向第二类的研究。

逆向物流网络可使一些有价值的产品得到回收再利用，并取得降低环境污染、提高资源利用率的目的。现有研究中，何波等[6]研究了由客户、回收点、回收中心组成的两阶段逆向物流网络设计问题，以最小化总运营成本为目标，建立了数学规划模型，并设计了模拟退火算法用于求解；熊中楷等[7]以回收中心利润最大化为目标，建立了混合整数规划模型，并通过粒子群算法求解；Demirel等[8]研究了由客户、回收中心、拆解中心、再制造厂组成的逆向物流网络问题，构建了混合整数规划模型，并采用CPLEX求解；Lee等[9]以总运营成本最小化为目标，构建了数学规划模型，求解方面采用了模拟退火算法；董景峰等[10]分析了由初级收集点、集中回收中心与回收处理工厂组成的逆向物流网络优化问题，以总运营成本最小化为目标，构建了数学规划模型，并设计了相应的遗传算法；黄铮[11]研究了由工厂、回收中心、客户组成的三级逆向物流网络，考虑到总成本最小化，建立了数学规划模型，并设计了启发式算法求解。

综观上述文献，在回收产品的处理方式方面与现实情况存在一定的差距。文献[6]与[7]均未对回收产品的处理情况进行规划，其所设计的逆向物流网络仅能保证产品会被送到回收中心，忽略了下一步的处理工作；文献[8]至[11]虽考虑了回收产品的下一步处理情况，但其均假定回收产品必须被送到工厂进行再制造，这一点并不符合实际情况。实际上，回收产品的质量有好有坏，甚至有些已经是报废品，将质量较低的产品送到工厂，从运输资源、成本角度来看完全是一种浪费。因此在回收中心对产品质量进行检测，并对不同类别的产品采用不同的处理方式是一项基本而重要的工作。

1 数学规划

1.1 问题描述

本文所设计的逆向物流网络结构如图1所示，由客户区域、回收检验中心、修复中心与垃圾处理中心组成，分为3个阶段。回收产品由回收检验中心从客户区域进行收集，并在回收检验中心进行质量检测，从而被分为两类产品：可再利用产品与废弃品。前者将被送到修复中心进行质量修复，并重新进入销售市场；而后者则被送到垃圾处理中心，以进行焚烧、填埋等处理工作。如前所述，该逆向物流网络有助于避免产生额外的运输成本，并可将合适的产品分配给合适的处理设施。

1.2 参数设置

定义I为可选的回收检验中心的集合，?i∈I；J为可选的修复中心的集合，?j∈J；K为可选的垃圾处理中心的集合，?k∈K；L为客户区域的集合，?l∈L。

r：回收产品中可回收再利用的比率，即经回收检验中心到达修复中心的比率；

d：客户区域l回收产品的供应数量；

c：客户区域l至回收检验中心i的单位运输成本；

f：回收检验中心i的年固定运营成本；

a：回收检验中心i至修复中心j的单位运输成本；

v：修复中心j的年固定运营成本；

g：垃圾处理中心k的年固定运营成本；

h：回收检验中心i的单位处理成本；

n：垃圾处理中心k的单位处理成本；

m：修复中心j的单位修复成本；

t：回收检验中心i至垃圾处理中心k的单位运输成本；

caf：回收检验中心i的最大产能；

cav：修复中心j的最大产能；

cag：垃圾处理中心k的最大产能。

决策变量：

q：从客户区域l到回收检验中心i的产品数量；

z：从回收检验中心i送达修复中心j的产品数量；

w：从回收检验中心i送达垃圾处理中心k的产品数量；

s：0-1变量，若选中修复中心j，s=1，否则为0；

p：0-1变量，若选中回收检验中心i，p=1，否则为0；

y：0-1变量，若选中垃圾处理中心k，y=1，否则为0；

1.3 数学模型

目标函数：

目标函数式（1）为逆向物流网络总成本最小，包括回收检验中心、修复中心与垃圾处理中心的固定成本、可变成本，以及3个阶段间的运输成本；式（2）表示每个客户区域的回收产品必须被作业；式（3）与式（4）对经过回收检验中心前后的产品数量进行了平衡约束；式（5）、式（6）、式（7）为产能约束；式（8）与式（9）限定了决策变量的取值范围。

2 遗传算法

从所建模型可以看出，该问题属于NP-hard问题，通过传统的精确算法，如分支定界算法，解决其大规模优化问题的效果较差。同时，鉴于遗传算法的并行计算效率与全局搜索能力较高，因此本文采用遗传算法求解。

2.1 染色体编码

根据模型特点，本文采用带优先权的整数编码规则。图2所示为4个客户区域、2个回收检验中心、4个修复中心与3个垃圾处理中心组成的染色体，分为3个子染色体，分别代表3个阶段的物流运作方案。其中，子染色体1由4个客户与2个回收检验中心组成，子染色体2由2个回收检验中心与4个修复中心组成，子染色体3由2个回收检验中心与3个垃圾处理中心组成，各子染色体的基因值分别代表该节点的优先权，基因值越大，优先权也就越大，则该节点的供给（或需求）情况也应该被优先处理。

2.2 染色体解码

3个子染色体的解码过程相同。解码时，依序分别对3个子染色体进行，即首先对子染色体1进行解码，然后是子染色体2的解码，最后是子染色体3的解码。以图2所示子染色体1为例，过程如下：

步驟1：选择子染色体1中基因值最大的节点，并对该节点的集合归属做出判断。如该染色体中最大的基因值为6，其对应客户区域2。

步骤2：从运输成本c矩阵中找出该节点对应的运输成本最小的另一集合节点，组成一个节点对。如在客户区域2对应的各回收检验中心的运输成本分别为13 15，则对应的节点为回收检验中心1，此时，（客户区域2，回收检验中心1）便组成了一个节点对。

步骤3：对该节点对的供应量与产能进行比较，选择两者中较小的量作为该节点对的物流量。如客户区域2的供应量为150，回收检验中心1的产能为200，则客户区域2到回收检验中心1的物流量为150。

步骤4：更新该节点对的相关信息。如客户区域2的供应量更新为0，回收检验中心的产能更新为50。

步骤：5：当该基因值对应节点的供应量（或产能）被完全满足时，将该基因值更新为0，并转步骤6执行；否则转步骤2继续执行。

步骤6：当客户区域的所有供应量均得到满足后，解码程序结束；否则转步骤1继续执行。

子染色体1染色体解码过程如表1所示。

子染色体1解码结果如图3所示：

2.3 初始种群与适值函数

为增强种群中个体的多样性，采用随机生成的方法，以提高遗传算法的全局搜索能力。在本文中，目标函数值越小，个体的适应度应该越大，因此，适值函数如下：

此外，采用轮盘赌的种群选择方式与精英保留策略。

2.4 交叉运算

交叉运算是生成种群新个体的一种重要方式，本文分别在各子染色体采用均匀交叉方式，见图4。

2.5 变异运算

通过变异运算，遗传算法可避免陷入局部优化情况，从而达到全局优化。针对染色体的特点，本文采用内部换位的变异方法，见图5。

3 算例实验

遗传算法采用MATLAB7.0编程实现，遗传算法与LINGO11.0软件均在2GB内存，intel Core i5-3210M 2.50GHz的处理器的计算机上进行测试。

3.1 具体算例

某城市有8个居民区域的产品需要回收，可回收再利用比率分别为50%，回收检验中心、修复中心与垃圾处理中心的相关数据如表2所示。

3个阶段逆向物流网络单位运输成本如表3所示。

算法参数通过多次实验获得：种群规模、交叉与变异概率、迭代次数分别为100，0.9，0.1，1 000。在MATLAB平台上设计遗传算法，程序运行133.52秒，目标函数值为81 190。求解结果见表4。

3.2 大规模实验

设计10组算例，相关参数如表5所示：

这10组算例均可通过LINGO11.0软件编程求解得出最优结果，以评价遗传算法的求解质量。遗传算法的基本参数设置同上节所示，迭代次数更新为50 000次，同时加入一个求解时间约束，即将求解时间设定为5分钟，时间到后算法即停止运算，并输出最优结果，并通过指标GAP=100%*（启发式算法优化解-LINGO最优解）/LINGO最优解，来对遗传算法求解效果进行评价，见表6。

从表6可以看出，10组测试算例中，本文所设计的遗传算法的GAP为0.36%～3.61%，求解效果非常理想。同时，从“计算时间”一项可以看出，随着算例规模的增大，LINGO软件的计算时间大大增加。在第10组算例中，求解时间用了将近16个小时，远远高于遗传算法求解时间。而第10组算例的GAP仅为3.61%，可见遗传算法的求解效率与求解质量都非常理想。

4 结束语

逆向物流网络设计是供应链管理的一项重要内容。本文基于对回收产品质量检验并分类处理的基础上，建立了新的3阶段逆向物流网络数学规划模型。考虑到其属于NP-hard问题，有针对性地设计了遗传算法，以求解其大规模优化问题。实验结果验证了模型与算法的有效性。在未来的研究中，可融入资金预算、供应不稳定性等现实因素。

参考文献：

[1] Altiparmak F， Gen M， Lin L， et al. A genetic algorithm approach for multi-objective optimization of supply chain networks[J]. Computers & Industrial Engineering， 2006，51：196-215.

[2] Lee D H， Dong M. A heuristic approach to logistics network design for end-of-lease computer products recovery[J]. Transportation Research Part E， 2008，44：455-474.

[3] Costa A， Celano G， Fichera S， et al. A new efficient encoding/decoding procedure for the design of a supply chain network with genetic algorithms[J]. Computers & Industrial Engineering， 2010，59：986-999.

[4] El-Sayed M， Afia N， El-Kharbotly A. A stochastic model for forward-reverse logistics network design under risk[J]. Computer & Industrial Engineering， 2010，58：423-431.

[5] Ramezani M， Bashiri M， Tavakkoli-Moghaddam R. A new multi-objective stochastic model for a forward/reverse logistic network design with responsiveness and quality level[J]. Applied Mathematical Modelling， 2013，37：328-344.

[6] 何波，孟卫东. 产品回收逆向物流网络设计问题的两阶段启发式算法[J]. 运筹与管理，2010，19（1）：73-79.

[7] 熊中楷，方衍，张聪誉. 以旧换新收购方式下的逆向物流网络优化设计[J]. 中国管理科学，2011，19（6）：65-72.

[8] Demirel O N， Gokcen H. A mixed-integer programming model for remanufacturing in reverse logistics environment[J]. International Journal of Advanced Manufacturing Technology， 2008，39：1197-1206.

[9] Lee D H， Dong M. Dynamic network design for reverse logistics operations under uncertainty[J]. Transportation Research Part E， 2009，45：61-71.

[10] 董景峰，王剛，吕民，等. 产品回收多级逆向物流网络优化设计模型[J]. 计算机集成制造系统，2008，14（1）：33-38.

[11] 黄铮. 废弃物回收逆向物流网络优化设计[J]. 系统工程，2009，27（7）：49-53.