利用“数学画”促进算法探究和算理理解———《分数除以整数》教学片断与思考

陈　昱

“数学画”教学缘起于低年级数学教学：受认知发展水平影响，低年级儿童对数学文本的认读和数学概念的理解比较困难，借助画图可以帮助儿童学习数学，并能使其爱上数学、探究数学，很好地发展数学思维。

“数学画”的表现形式是图画，低年级学生乐于绘画，“画数学”比“写作业”对他们更具吸引力。随着学习的推进和展评课的引导，“数学画”中“非数学”成分逐渐减少，教师应有意识地引导学生在创作中运用箭头、省略号、问号、括号、虚线、圈线、几何图形以及算式等数学符号，尽量用几何图形等代替具体物象，绘制物象时力求简洁，逐渐数学化。中高年级的“数学画”将渐变成“示意图”、“线段图”、“知识结构图”等形态。

本课就是高年级“数学画”教学的一次很好的尝试。

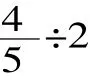
师：同学们，老师这儿有一个数学问题，我们一起来看一看：

师：对于这个问题，你打算用什么方法来解决？

生1：用除法来做。

师：为什么呢？

生2：因为这是平均分问题。

生3：以前都是整数除法，现在是分数除以整数。

生4：可以画图看一看。

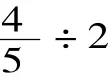
（学生独立画“数学画”解决问题，全班交流）

师：这儿有几幅作品，一起来看看！

1.展示生1作品：

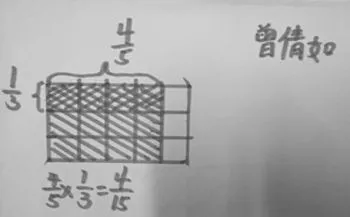
生：这个长方形代表一张纸，把它平均分成5份，取其中的4份，就是这张纸的，把它画上斜线。要把一张纸的平均分成2份，它有4份，平均分成2份就是一半，是2份，我把它涂上颜色，就是（这张纸的）。

师：你的思考过程我能不能这样记录呢？

师：你们有没有问题？

2.展示生2作品：

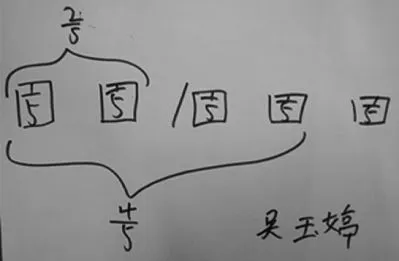
师：谁能看懂这幅作品？请你说说看。

生：我用一个圆形代表1张纸，把它平均分成5份，每份是其中的，4个是，把4个平均分成2份，每份是2个，就是，所以

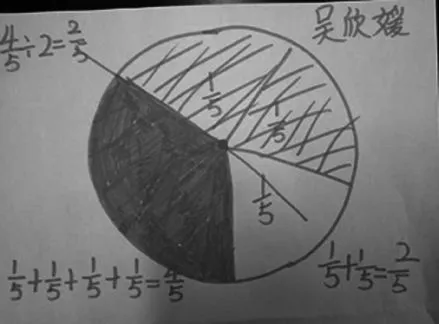
师：我们可以画出不同形态的“数学画”来表示思路，很有个性！

生：我的思路也是这样的！不过我画的是线段图。

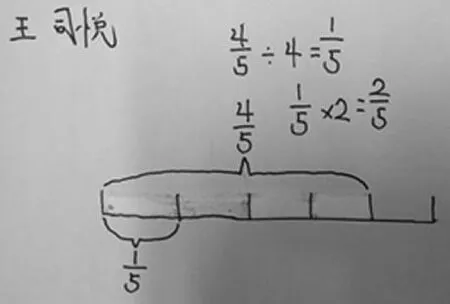
3.展示生3的作品：

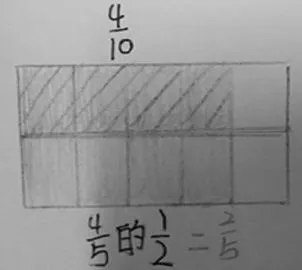
师：这幅作品好像有些特别，你能看懂吗？

生：为什么分成了10份？

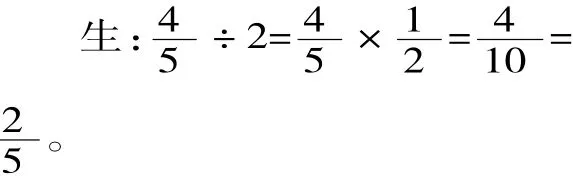
师：谁来说给全班同学听一听？

生1：分数除以整数，可以用分子除以整数（作分子），分母不动。

生2：分数除以整数，要看除以几，除以几就等于乘几分之一，比如除以2就等于乘上。

生3：也就是乘整数的倒数就行了！

生4：我认为分数除以整数有两种方法，一种是用分子除以整数；一种是乘上整数的倒数。

【教学思考：“数学画”教学的重要特点之一便是充分尊重学生数学学习的差异性。

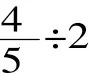
当然，学生的精彩不只体现在“数学画”形态以及背后数学思维的多样性方面，更体现在学生展示“数学画”环节的语言表达和互动评议方面。有了“数学画”，原本抽象的算理变得直观，原本难以把握的思路变得有迹可循。】

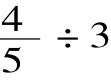
师：现在你还会解决它吗？拿出2号白纸画一画、算一算吧！

（学生画“数学画”探究，全班交流）

师：哪些同学已经解决了这个问题？谁愿意上台跟大家分享你的探究过程？

师：你们听懂了吗？（同学们点头）和她一样的请举手！（大部分同学举起手）那你能把算式完整地写出来吗？

师：刚才有几位同学没举手，是什么情况？

生：我是用第一种方法，但是发现4不能分成3份，4除以3除不了！

生：其实第一种方法也可以的。

师：到底行不行。让我们听一听，带上你的作品上来说。

生：我发现第一种方法分不了，4不能整除3，到这里就堵住了。我想了想，怎样才能整除3呢？于是我想起以前学过分数的基本性质，就把分子分母同时扩大3倍，就变成，也就是每个里都再平均分成3份，这时候就能够除以3了，12除以3等于4，每份是这张纸的。

师：让我们一起来记录他的计算过程。

师生共同完成：

小组讨论。

师：怎么样？有想法了吗？谁来说一说？

生1：本来我认为第一种算法不太好，有时候不行，第二种算法比较好，不管什么情况都行。但是，现在我发现第一种算法其实也是行的，只不过比较麻烦，有时候要先乘再除。

生2：我们小组认为两种算法是有联系的，最后都可以转化成乘这个数的倒数。

师：你们赞同吗？（有的点头，有的在思考）再请一位赞同的同学上台结合算式说一说，谁愿意？

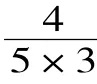
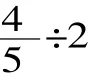
在如此精彩自然的课堂生成面前，我之前精心制作的动画课件显得“黯然失色”，也就没有展示的必要了。所以，这个环节的课堂完全是“缘学而教”，感觉棒极了！

总而言之，本课引入“数学画”教学“分数除以整数”，重视从儿童视角出发，关注数学素养的培育，为学生搭建了数学学习和课堂展示的平台，达到了预期目标，并超越预设收获了更多的精彩！】