无痕教育的课堂实践策略
——以《解决问题的策略》教学为例
徐 斌(特级教师)

理想的教育境界是教育无痕,然而“有”和“无”并不是完全对立矛盾,而是具有内在联系的统一体。如何处理有痕与无痕之间的辩证统一关系呢?有痕,体现的是基础知识和基本能力的显性变化;无痕,体现的是必备品格和关键能力的隐性提升。有痕,更多地表现为课堂组织设计的精致与细腻;无痕,更多地表现为课堂教学过程的灵动与开放。有痕与无痕,是互相依存的和谐统一。要达到无痕的境界,需要经历有痕的阶段。在我看来,教育的最终目的是要让学生获得带得走、看不见而又用得着的东西,即当下都在研究与提倡的核心素养。核心素养是学生发展的“隐形的翅膀”,具有“无形的力量”,如同武侠小说里面的“手中无剑,剑在心中”。无痕教育理念下的数学课堂实践策略有哪些呢?下面以六年级《解决问题的策略:替换》一课的教学为例,阐述其教学实施策略。
一、不知不觉中开始
良好的开端是成功的一半,数学学习活动的开启,应该在自然而然中出发,而不是赤裸裸地灌输和强制性接受。只有引发了对新知的内在需要,才能激发起学生学习的内驱力。而要做到“不知不觉中开始”,前提是教师对所教内容的整体把握。优秀的教师总是能够瞻前顾后、迁移渗透,把握所教内容与以前学习内容以及将来学习内容之间的实质性联系,帮助学生选准合适的认知起点,让学生在不知不觉中开始新知学习。
片断1:引入“替换”的策略
(依次出示两幅天平图,引导学生观察思考)
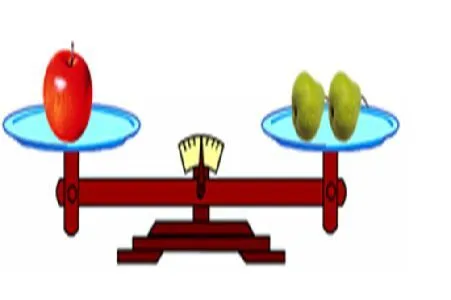
图1
师:这是一架平衡的天平,从图中你能看出一个苹果的重量和一个梨的重量之间有什么关系吗?(图1)
生:一个苹果的重量是一个梨的两倍。
师:据两幅天平图,你能求出一个苹果和一个梨的重量吗?
生:把图2中左边的一个苹果换成两个梨,就成了4个梨重400克,这样可以求出一个梨重100克,再求出一个苹果重200克。
生:把图2中左边两个梨换成一个苹果,就是两个苹果重400克,一个苹果就重200克,再求出一个梨重100克。
(课件动态演示把一个苹果换成两个梨或者把两个梨换成一个苹果)
师:在解决刚才这个问题时,大家用到了“换”的方法,这是数学中一种非常重要的策略——替换。(板书)
师:其实早在一千七百多年前有一个叫曹冲的小朋友,就用替换的策略演绎了一个生动的故事,你们听说过吗?
师:(出示“曹冲称象”的图片)曹冲是如何用替换的办法称出了大象的重量?
生:曹冲是用石头替换大象的。
【解读:如何让学生在不知不觉中产生运用替换策略的需要?上述教学片断中,通过形象直观的方式引发了学生的初始学习进程。学生虽然是第一次正式学习用替换的策略解决问题,但在他们的生活经验中已模糊地经历过类似的方法,只是还没有建立起一种完整的数学模型。所以在课的引入部分,从直观的天平图,到感性的数形结合,再到抽象的推理计算,并结合“曹冲称象”的典故,一下就扣住学生心理,唤醒了他们头脑里的已有生活经验,为之后的探究过程奠定了良好的心理准备和认知基础。】
二、潜移默化中理解
“为理解而教”是数学教学的重要目标,而理解知识的关键是顺应学生的思维特点和认知规律。小学阶段学生的认知水平属于“具体运算思维”阶段,其最大的特点是思维离不开具体事物的支持,他们的感知觉、观察力和记忆均处于初步发展水平,学习数学的动机和兴趣也很不稳定。在这样的前提之下,小学生学习数学的过程,需要充分借助形象直观的教学手段,充分利用新旧知识的相互作用,以顺应学生的学习心理,让他们在不露痕迹中获得新知意义。
片断2:理解“替换”的本质
例题:小明把720毫升果汁倒入6个小杯和1个大杯,正好都倒满。小杯的容量是大杯的小杯和大杯的容量各是多少毫升?

生:大杯容量是小杯的3倍。
生:1个大杯可替换成3个小杯。
生:3个小杯可替换成1个大杯。
师:怎样用替换的策略来解决这个问题呢?谁能把你的方法介绍给大家?
生:我把1个大杯换成3个小杯,这样就有9个小杯,一共是 720 毫升,720÷9=80,可以算出一个小杯的容量是80毫升,一个大杯的容量就是240毫升。
生:我是把6个小杯换成2个大杯,这样就有3个大杯,720÷3=240,先求出一个大杯的容量是240毫升80,再求出一个小杯的容量是80毫升。
师:如果把题中条件改成“大杯的容量比小杯多20毫升”,现在还可以替换吗?
生:我认为不好替换。因为不是正好装720毫升果汁。
生:我认为似乎可以替换,就是替换之后有可能720毫升果汁装不下。
生:我也认为可以替换,不过替换之后也有可能不止装720毫升果汁。
师:请同学们在练习纸上画图试一试,看看能否解决问题。不过要特别注意——在替换时,果汁的总量会有什么样的变化?
(教师完成板书)

【解读:如何让学生在潜移默化中理解替换策略的本质?上述片断中,先让学生自主分析数量关系,然后组织小组讨论寻求策略,接着独立画图感悟思考,最后师生交流,教师用简洁明了的板书加以体现。尤其是板书的设计具有启发性,采用箭头符号,让学生直观地感知大、小杯替换的过程。在学生初步学习了倍数关系的替换策略之后,教师抓住替换的依据进行变式,由“小杯的容量是大杯的”改变为“大杯的容量比小杯多20毫升”。当学生对两个数量呈相差关系能否进行替换产生不同意见时,适时组织学生讨论、辩论,从而获得问题的解决。这样的设计与教学,抓住两个量之间的关系,灵活变化,充分调动了学生的探究欲望,利用知识间的迁移,突破了难点,并让学生在比较中内化已有知识结构,明确了倍比、差比两种不同类型的替换特征,在变化与不变中让学生探寻联系,感受到数学的规律美。】
三、循序渐进中掌握
学生学习数学的过程,既是在教师引导下的意义建构过程,也是在自身需求发展中的自主建构过程。数学教学是一种层次艺术,更是一种“进”与“退”的智慧。通过适当的“退”和必要的“进”,能使得学习过程成为学生潜移默化地掌握知识和技能的过程。表面上看,“进”和“退”是一对反义词,然而,这两者并不矛盾。从某种意义上说,“退”是“进”的准备和基础,“进”是“退”的发展与提升。在课堂上,“进”“退”之间体现的是一种行云流水般的从容节奏,是一种水乳交融般的无痕状态。
片断3:掌握“替换”的策略
1.学生独立审题,填写替换的方法,不必列式计算:
(1)六(1)班 50名同学和杨老师、杜老师一起去参观机器人科普展,买门票一共用去270元。已知每张成人票是每张学生票的两倍,每张学生票多少元?每张成人票多少元?
想:把它们都看成( )票,可以把()张()票换成()张()票。那么270元相当于买了()张()票。
(2)在两个同样的大盒和五个同样的小盒里装满球,正好是100个。每个大盒比每个小盒多装8个,每个大盒和每个小盒各装多少个?
想:如果把( )个( )盒换成()个( )盒,总个数比原来( )(填“多”或“少”)()个。
2.你能运用替换的策略解决这个问题吗?

(部分学生看到题目就开始列式,部分学生没有马上列式,少数学生举手发问)
生:这道题似乎缺少什么条件?
生:这道题目没有告诉我们铅笔和钢笔单价之间的关系,因此不能做。
师:不错,聪明的同学善于发现问题!如果运用替换的策略,就需要明白替换的依据。那么,要想用替换的策略解决这个问题,可以补充什么样的条件?
生:可以补充倍数关系的条件,也可以补充相差关系的条件。
【解读:有效的数学课堂不能止步于理解。为促进学生从理解走向掌握,上述片断中设计了两个层次的巩固练习:前两题是独立审题并填写替换方法,进行基础性练习,其实是一种“退”;最后一题是缺少条件的替换问题,让学生尝试与讨论,并补充相关条件,其实是一种“进”。这样的设计与教学,学生在循序渐进中逐步走向替换策略的本质,形成相关技能,进而应用技能解决简单的实际问题。】
四、春风化雨中提升
课堂学习的过程就是学生不断发展和提升的过程。如何提升学生的数学素养?有道是:比知识更重要的是方法,比方法更重要的是思想,比思想更重要的是精神。课堂是师生人生中一段重要的生命经历,课堂是充满无限魅力的地方,课堂是学生充分发展的天空。无痕教育理念下的数学课堂,学生的学习经历应是充实快乐的,学习结果应是充分有效的,学习的过程应是充满智慧的。
片断4:拓展“替换”的策略
师:刚上课时,我们观察了天平图,采用了替换的策略分别求出了两种水果的重量。现在我们继续观察天平图。
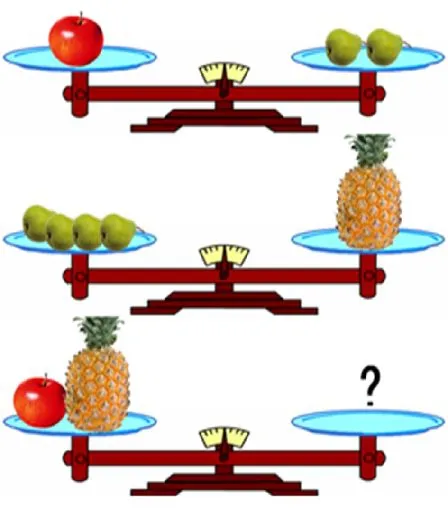
师:第一幅天平图,显示了两种水果之间的重量关系;第二幅天平图,出现了第三种水果——菠萝;第三幅天平图,右边托盘里,如果放同一种水果,可以怎样放?
生:可以放6个梨。
生:可以放3个苹果。
生:可以放一个半菠萝。
师:如果右边托盘里放了一个600克的砝码,天平保持平衡。你能分别求出一个梨、一个苹果和一个菠萝的重量吗?
【解读:学生学习数学的重要价值在于发现生活中的数学问题,并能利用所学的知识去解决问题。数学又是思维的体操,思维的灵活性、开放性、应变性直接关系到学生学习能力的高低。本课主要学习的是两个量之间的替换,而此题已经拓展为三个量之间的替换,学生的思维能力得到极大的提高与开发。在课的结尾再次结合课始的直观天平图,并进行拓展和延伸,让学生感受到替换策略的作用,去寻找生活中的替换现象,并从数学的角度去研究这些现象,进而从数学策略上升为数学思想,乃至于数学的理性精神。】

