基于切换模糊化的车辆速度滑模控制方法*

高 嵩 吕军锋 陈超波 曹 凯

(西安工业大学电子信息工程学院 西安 710021)

基于切换模糊化的车辆速度滑模控制方法*

高 嵩 吕军锋 陈超波 曹 凯

(西安工业大学电子信息工程学院 西安 710021)

针对电动汽车速度控制模型的非线性和时变性特点,设计了滑模控制器控制车辆速度,使系统具有较强鲁棒性,并通过模糊算法调节滑模控制器切换函数的参数,降低了滑模控制器固有的抖振。切换模糊化处理后的滑模控制器控制输入切换频率大大降低,减少了控制机构的频繁切换,提高了控制机构的稳定性。仿真结果表明,该控制器能准确快速地跟随给定速度,对外部环境变量扰动和自身参数变化扰动具有较好的适应性和较强的鲁棒性。

速度控制; 滑模控制; 切换模糊化; 模糊控制; Simulink仿真

Class Number TP391

1 引言

速度跟随控制在自主无人车控制中有较多的应用,例如在无人车车队中后车对前车速度的跟随控制,单个自主无人车中下位机对上位机给出的参考速度的跟随控制等。在无人车车队中的应用是通过图像传感器或者测距传感器得到前车的实时速度,并进行速度跟随的控制。在单个自主无人车中的应用是由上位机通过机器视觉感知周围环境,进而给出期望速度,由下位机进行跟踪的控制。自主无人车的速度跟随控制系统易受外界环境因素和车辆轮胎以及电机自身特性影响,导致控制模型是非线性的,在实际建模时一般的处理方法是将某些非线性的部分当做干扰在建模过程中忽略,而在控制算法中通过提高系统的鲁棒性来减小建模过程中忽略的非线性部分对系统性能的影响。

近些年,国内外学者在车辆的跟踪控制方面已有许多探索和研究,并已取得了一定的成果。Peppard L[1]设计的速度控制器使用经典的PID控制算法,算法简单,适用于经典的线性跟随系统。Yi K,Hong J等[2]提出了前馈控制与PI反馈控制相结合的方法,车辆纵向控制方案由一个速度控制算法和距离控制算法以及油门制动控制律构成,对被控对象的不确定性有良好的适应性。Bageshwar V L等[3]采用模型预测方法设计了显式控制器,解决了在线MPC模型复杂,计算量大,控制实时性不够的问题。J. Aracil[4]应用模糊理论构建车辆控制非线性模型,在跟随系统的稳定性、时滞性问题做出了研究。Muller R等[5]提出了模块化模糊控制器,将实际的道路情况以及道路环境等干扰情况都考虑到了控制系统中,利用模糊算法来控制车辆跟随期望速度。李果等[6]针对车辆纵向控制非线性模型,提出了基于反馈误差信号的的迭代控制算法,该算法有较好的鲁棒性。任殿波、张继业等[7～8]应用向量Lyapunov函数方法和比较原理,研究了具有时间滞后的车辆纵向跟随系统的指数稳定性问题,并采用滑模方法设计控制器,使跟踪误差有较快的收敛速度。目前在车辆的速度跟随控制研究中,前面的研究或者忽略了车辆模型的非线性部分,或者通过模糊控制模拟了车辆纵向非线性模型,或者通过复杂的控制器来解决系统的非线性。所以,建立简单可靠的车辆纵向模型同时提高系统抗干扰能力、削弱道路模型和其它环境变量对跟随系统的影响等方面还需要继续研究。

在本文中,建立车辆速度跟随系统模型时考虑了风速和道路坡度的影响,利用滑模控制算法增加了系统鲁棒性,并对应用模糊函数的万能逼近原理实时调节滑模算法切换函数的参数,减小系统的抖振,提高了系统的适应性和抗干扰能力。本文所做的研究如下:首先,根据车辆运动学模型和电机经验模型建立了车辆速度跟随系统模型。接下来,根据滑模变结构理论,设计滑模面和控制律,构建了车辆纵向速度跟随滑模控制器。接着对常用的切换函数进行改进,利用模糊原理对切换函数参数进行模糊调节,并在Matlab的Simulink模拟环境中搭建系统,代入实际的车辆参数,外部环境变量摄动等干扰,进行对比仿真实验。

2 车辆纵向速度跟踪的数学模型

2.1 轮胎受力数学模型

如图1所示轮胎的动力学模型可表示为

(1)

其中,Te为作用在驱动中上的力矩,Fx为路面摩擦力,Fz为车胎受到地面的反作用力,ω为车胎角速度,J表示轮胎转动惯量,r为车胎半径。

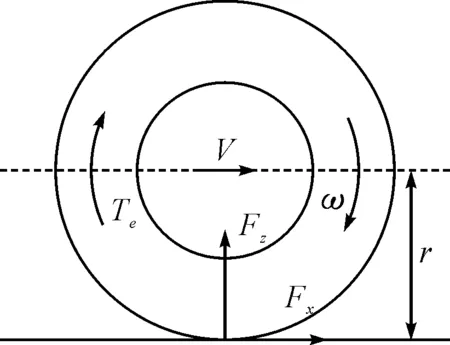
图1 车胎运动模型示意图

2.2 车辆受力数学模型

如图2所示,忽略风速在车辆行驶方向上的分量对风阻力的影响,车辆在运动方向上的动力学方程可表示为

(2)

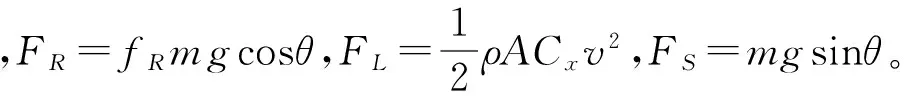
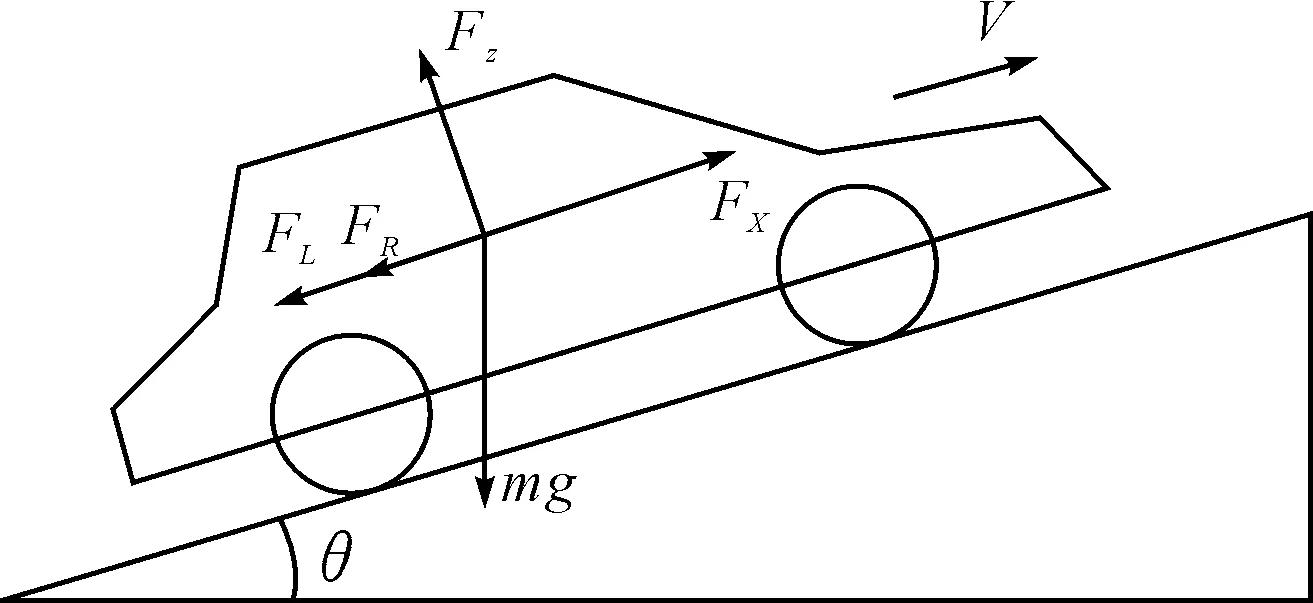
图2 车辆受力示意图

m为车辆质量,v为车辆纵向速度,FR为滚动阻力,FL为风阻力,FS为坡阻力,fR为滚动阻力系数,θ为路面坡度,ρ为空气密度,A为车辆迎风面积,Cx为空气阻力系数。

2.3 电机系统数学模型

根据经验公式可得电机系统模型可由下面的一阶模型表示:

(3)

Tl为电机输出力矩,Treq为电机系统输入力矩,τ为时间常数。将式(3)转化成微分方程形式

(4)

2.4 车辆速度跟踪系统数学模型

本文的建模过程中假设减速器和电机输出轴之间的连接为刚性的,则可认为电机输出力矩Tl和作用于驱动轴上的驱动力矩Te成比例关系,设传动比为R，则可得:

Te=R·Tl

(5)

设[x1x2]=[vTe],u=Treq,综合上述的轮胎运动模型(1)、车辆受力模型(2)和电机系统模型(4)、(5)可以得到车辆速度跟踪控制系统为

(6)

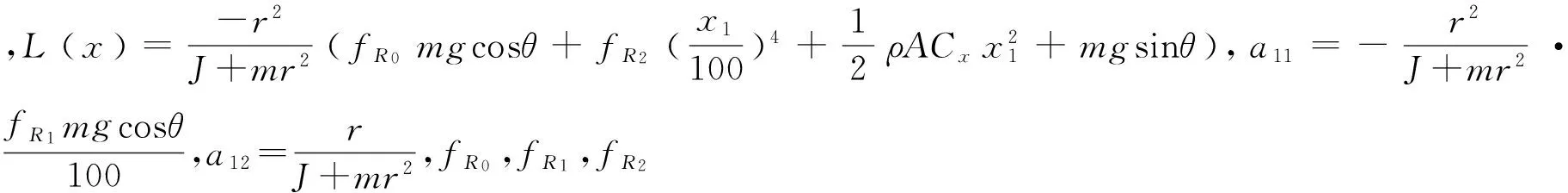
3 模糊滑模控制器设计

本文中被控对象是车辆的速度,易受外界道路状况横向速度和车辆自身参数影响,因此,本文中使用滑模控制来使系统具有较好的鲁棒性,同时利用模糊算法实时改变控制律参数来降低系统的抖振。

滑模控制器的设计主要包括滑模面的设计和趋近律的设计。进而就可以得到系统的控制输入。

3.1 滑模控制器设计

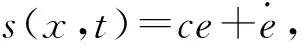
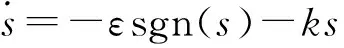
(7)

则得到的控制输入为

(8)

υ为控制律的辅助项,ε>0,k>0。

(9)

将u代入得

(10)

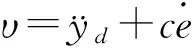
(11)

由此可以证明系统滑动模态存在,并可以在有限时间内到达[15]。

3.2 模糊切换面设计

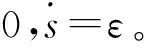
由以上分析可得模糊控制规律为:当|s|较大时,控制律中选取较大的ε和较小的k,来保证系统满足控制输入u的前提下,有较大的趋近速度;当|s|较小时,控制律中选取较小的ε和较大的k,保证系统有一定趋近速度的情况下,减小抖振。

基于以上控制规则可令

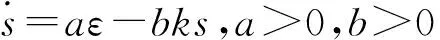
(12)

则在控制过程中就可以对a,b和输出s进行模糊化来间接地调节ε和k的值。定义a,b和s的模糊集合分别为{A-2,A-1,A0,A1,A2},{B0,B1,B2}和{C-2,C-1,C0,C1,C2}。设a和s的模糊语言变量的符号为:{NB,NS,ZO,PS,PB},b的模糊语言变量符号为{PS,PM,PB},其中,NB=负大,NS=负小,ZO=零,PS=正小,PM=正中,PB=正大,则设计模糊控制规则表如表1所示。系统的模糊输入隶属度函数和模糊输出隶属度函数如图3～图5所示。

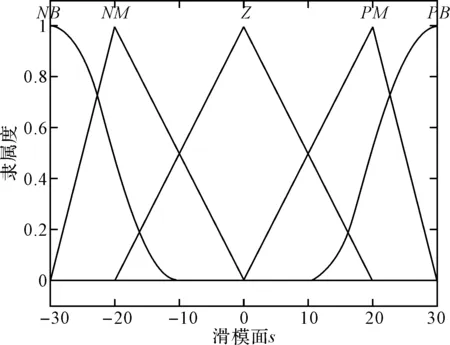
图3 模糊输入的隶属函数

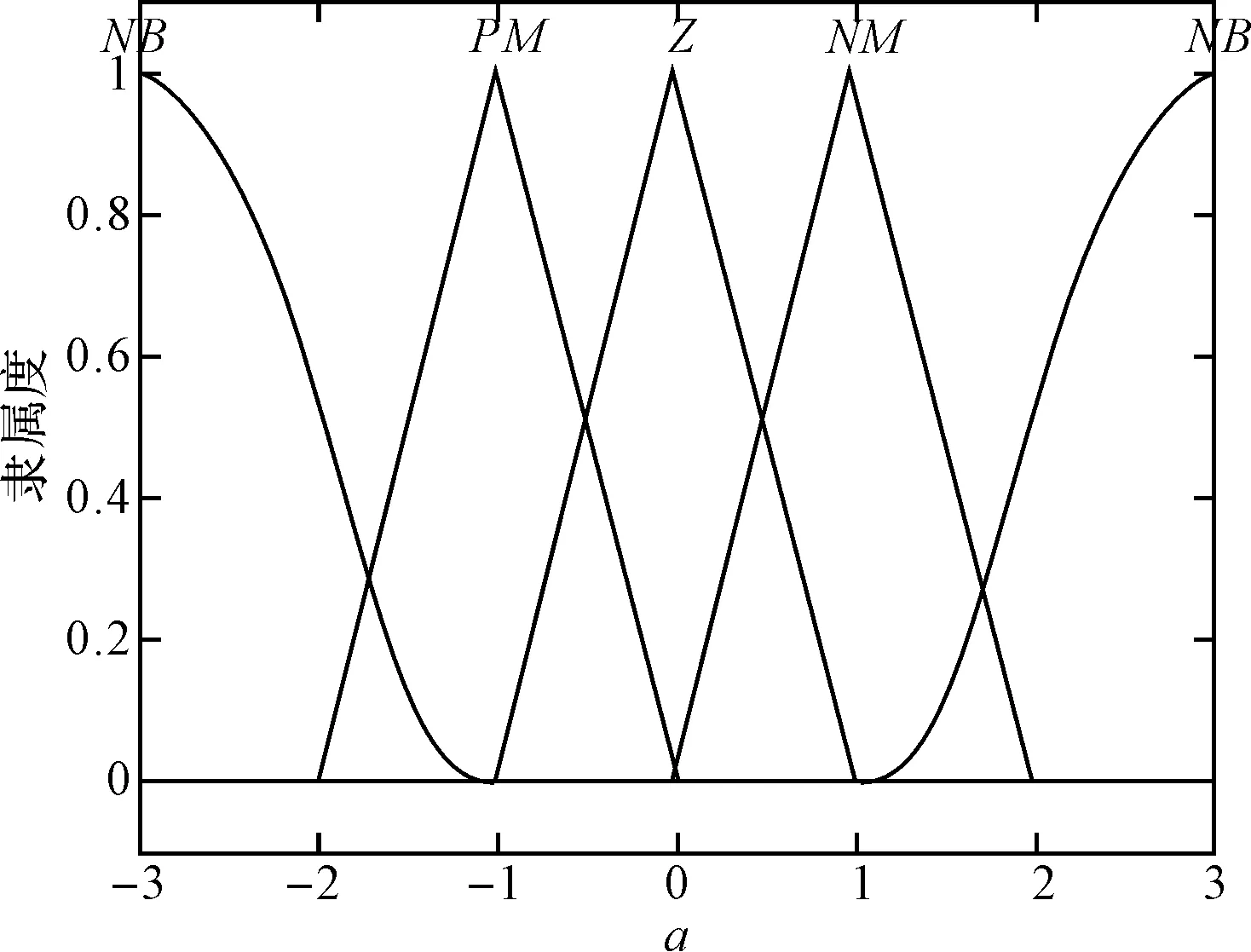
图4 模糊输出a的隶属函数

图5 模糊输出b的隶属函数

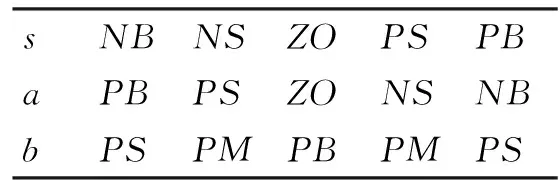
表1 模糊控制规则表

采用单元集模糊化、max-min推理合成规则和重心清晰化的方法得到a,b清晰化的控制量为

(13)

(14)

此时的控制输入u变为

(15)

4 仿真研究

设置控制器的参数为c=12,ε=5,k=80,控制式取式(15)。某型号汽车的参数如表2所示。

表2 某型号汽车参数

用正弦波信号yd=10sin(0.5t)+11作为理想的速度跟踪轨迹在Simulink仿真环境中设计控制系统仿真实验,仿真结果如下。

在无外界干扰的情况下得到的跟踪曲线和误差曲线的仿真结果如图6所示。

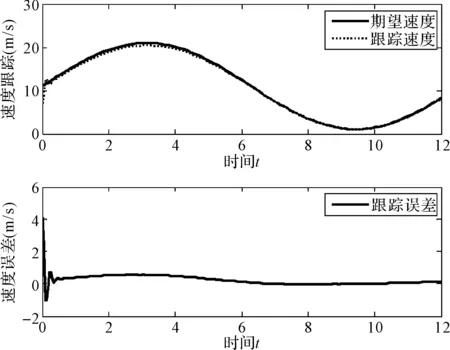
图6 无扰动情况下跟踪曲线和跟踪误差

为了说明该系统的鲁棒性,在此加入高斯函数干扰如图7所示,来模拟实际车辆行驶当中由于路面或风速变化造成的输入到车辆系统的力矩的突然变化,仿真结果如图8所示。

通过与没有干扰存在的情况下的仿真结果(图6)比较可知,加入高斯干扰后(图8),在高斯函数的峰值t=3的时刻附近,跟踪误差有一个小的波动,但整体的误差还在允许的范围内。说明控制系统对输入力矩的突然变化有较好的鲁棒性。即控制系统对路面的变化具有较好的适应性和鲁棒性。

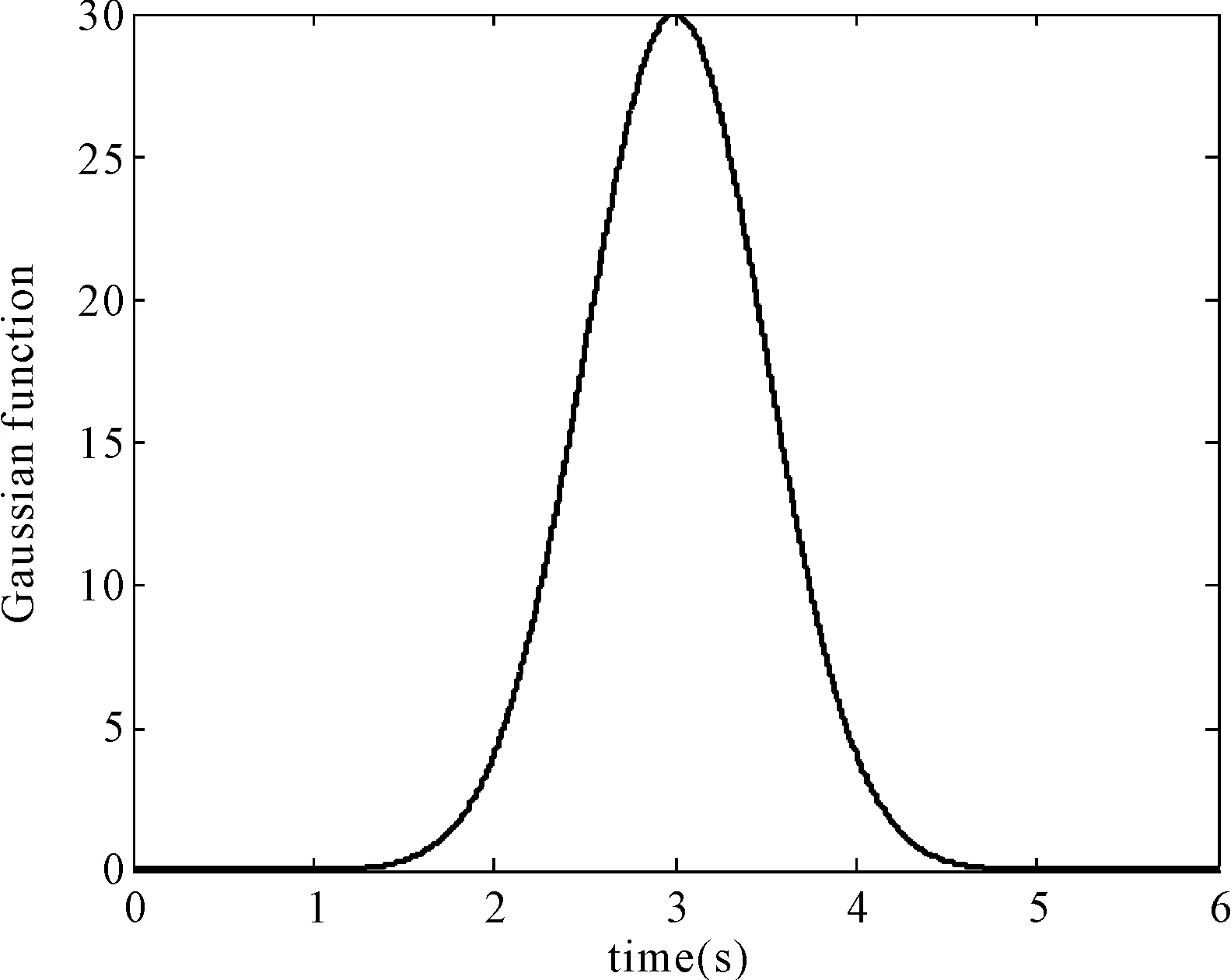
图7 高斯扰动函数

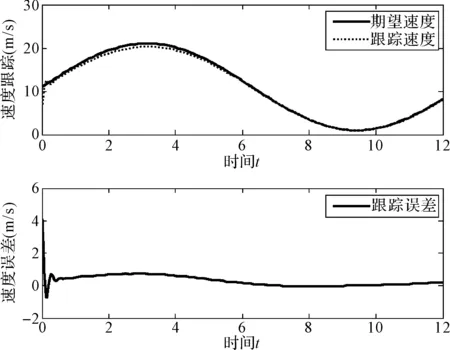
图8 加入高斯扰动情况下跟踪曲线

为了研究切换模糊化滑模方法和滑模方法的控制性能,本文设计了对比实验，在存在高斯扰动的情况下对比两种方法的控制性能。仿真结果如图9所示。对比结果表明,切换模糊化滑模算法和滑模算法都能较好地跟踪给定速度,切换模糊化算法在消除抖振方面有较大的改善,如图9(b)所示,图中曲线表示控制输入沿滑模面切换的趋势,在图中可以看出切换模糊化滑模算法的切换次数和切换幅值较滑模算法都有较大的改善,切换次数减少了,切换幅度变小,切换更平缓。这对实际应用中控制系统的控制是极为有利的,减少了控制机构的来回摆动,在速度跟随控制系统中则体现出的是减少了输入力矩变化的频率和幅度,减少了机械损耗。

以上的仿真和对比实验表明,切换模糊化滑模控制器可以使系统快速的跟随给定速度,且对外部随机扰动有较好的适应性和鲁棒性,与滑模方法相比能较好的减小抖振,增加系统的稳定性和适应性。

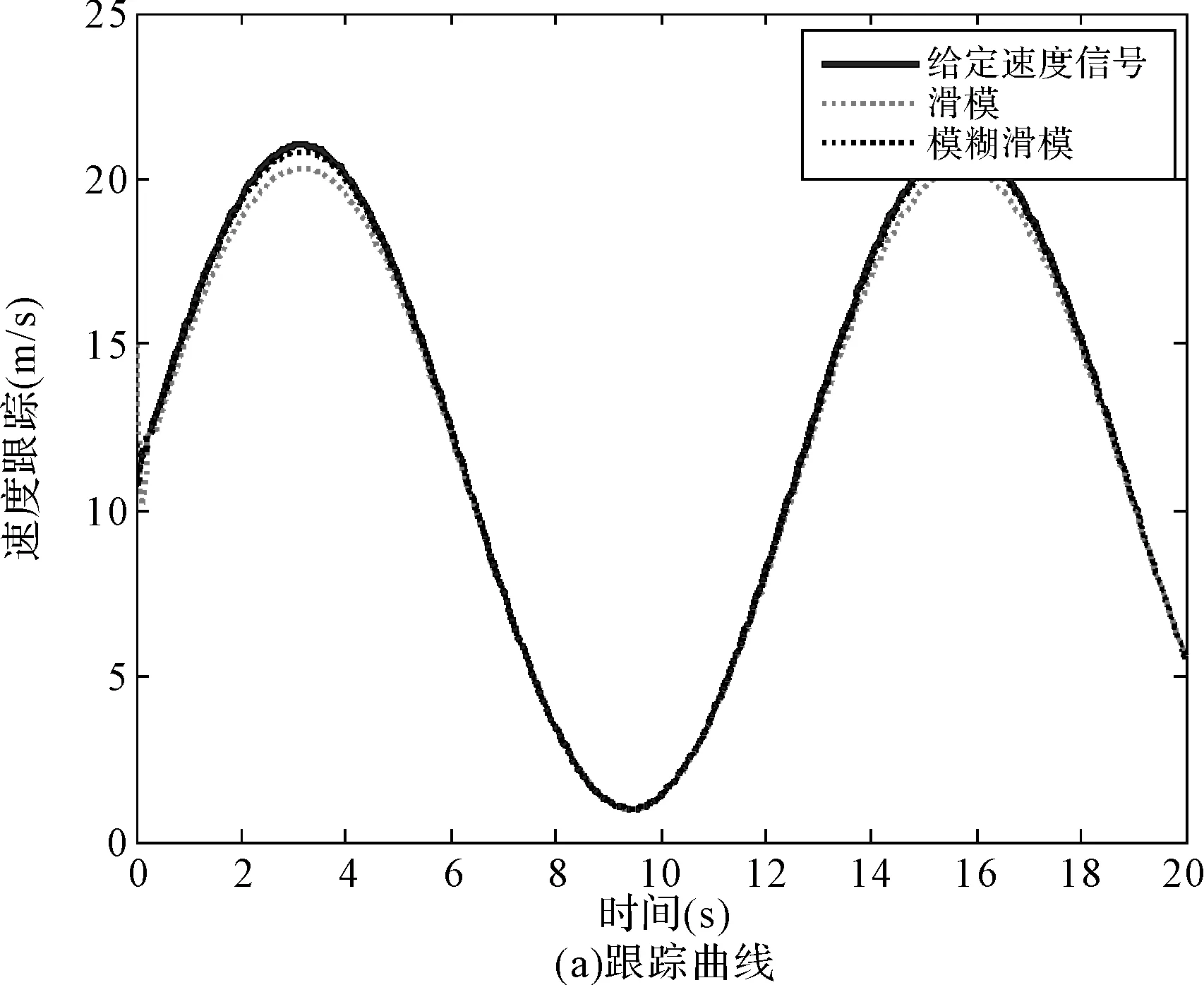
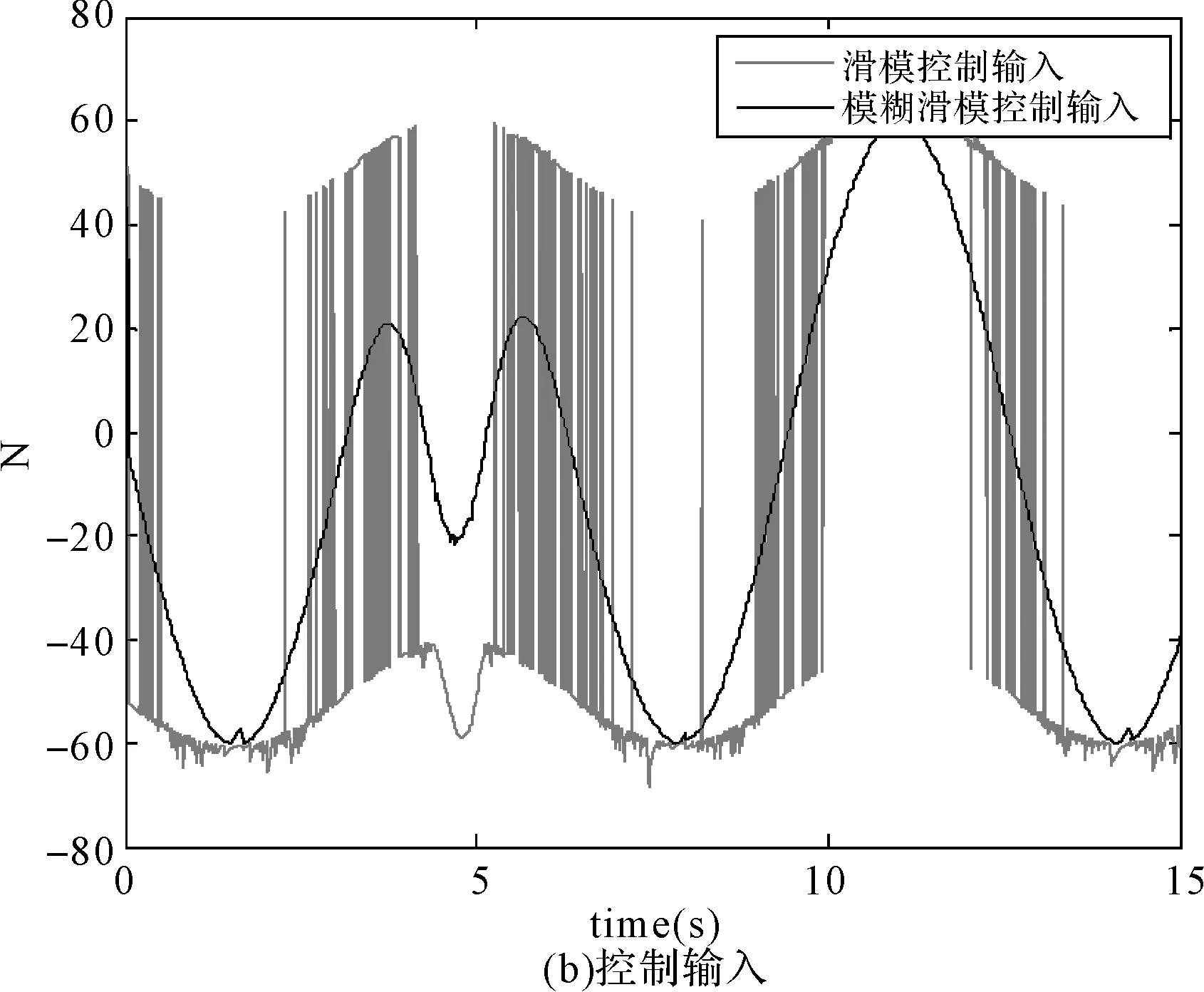
图9 模糊滑模方法和滑模方法控制性能对比

5 结语

本文根据模糊理论和滑模控制方法,设计了车辆速度滑模控制器,该控制器对外部干扰和自身参数波动有较好的适应性。利用模糊函数的万能逼近原理,设计模糊算法调节滑模控制器切换函数的参数,柔化了系统的控制输入,有效地降低系统了抖振,减小了机械系统来回切换造成的机械损伤,提高了控制系统的动态性能。

[1] Peppard L. String stability of relative-motion PID vehicle control systems[J]. Automatic Control, IEEE Transactions on,1974,19(5):579-581.

[2] Yi K, Hong J, Kwon Y D. A vehicle control algorithm for stop-and-go cruise control[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering,2001,215(10):1099-1115.

[3] Bageshwar V L, Garrard W L, Rajamani R. Model predictive control of transitional maneuvers for adaptive cruise control vehicles[J]. Vehicular Technology, IEEE Transactions on,2004,53(5):1573-1585

[4] J. Aracil, G. Heredia, A. Ollero. Global stability analysis of fuzzy path tracking using frequency response[J]. Engineering Applications of Artificial Intelligence,2000,13(2):109-119.

[5] Muller R, Nocker G. Intelligent cruise control with fuzzy logic[C]//Intelligent Vehicles’92 Symposium, Proceedings of the IEEE,1992:173-178.

[6] 李果,张良起,张彭,等.汽车纵向控制系统的设计与研究[J].自动化学报,1996,5:582-586. LI Guo, ZHANG Liangqi, ZHANG Peng, et al. Design and Research on vehicle longitudinal control system[J]. Acta Automatica Sinica,1996,5:582-586.

[7] 任殿波,张继业,李维军.基于滑模控制的时滞自动车辆跟随系统数学模型[J].公路交通科技,2008,1:142-145. REN Dianbo, ZHANG Jiye, LI Weijun. Mathematical Model of Automated Vehicle Following System with Delay Based on Sliding Model Control Method[J]. Journal of Highway and Transportation Research and Development,2008,1:142-145.

[8] 任殿波,张继业.基于Lyapunov函数方法的时滞车辆纵向跟随控制[J].控制与决策,2007,8:918-921,926. REN Dianbo, ZHANG Jiye. Lyapunov function approach to longitudinal following control of vehicles in platoon with delays[J]. Control and Decision,2007,8:918-921,926.

[9] 孔小兵,刘向杰.基于输入输出线性化的连续系统非线性模型预测控制[J].控制理论与应用,2012,2:217-224. KONG Xiaobing, LIU Xiangjie. Continuous-time nonlinear model predictive control with input/output linearization[J]. Control Theory & Applications,2012,2:217-224.

[10] 高嵩,刘海龙,陈超波.车辆导航横向模糊滑模控制算法及性能仿真[J].西安工业大学学报,2015,12:1010-1015. GAO Song, LIU Hailong, CHEN Chaobo. Design and Performance Simulation of Fuzzy Sliding Mode Lateral Control Algorithm for Vehicle[J]. Journal Of Xi’An Technological University,2015,12:1010-1015.

[11] Nouveliere L, Mammar S. Experimental vehicle longitudinal control using a second order sliding mode technique[J]. Control Engineering Practice,2007,15(8):943-954.

[12] Parra-Vega V, Hirzinger G. Chattering-free sliding mode control for a class of nonlinear mechanical systems[J]. International Journal of Robust and Nonlinear Control,2001,11(12):1161-1178.

[13] Chong K T, Roh D H. A Lyapunov function approach to longitudinal control of vehicles in a platoon[J]. Vehicular Technology, IEEE Transactions on,2001,50(1):116-124.

[14] J.Y. Wong. Theory of Ground Vehicles. John Wiley & Sons,1978.

[15] 刘金琨.滑模变结构控制MATLAB仿真:基本理论与设计方法[M].第3版.北京:清华大学出版社,2005:39-40. LIU Jinkun. Sliding Mode Control Design and MATLAB Simulation[Third Edition] The Basic Theory and Design Method[M]. Beijing: Tsinghua University Press,2015:39-40.

Sliding Mode Control Method Based on Fuzzy Switch Function for Vehicle’s Speed

GAO Song LV Junfeng CHEN Chaobo CAO Kai

(School of Electronic Information Engineering, Xi’an Technological University, Xi’an 710021)

Electric vehicle’s longitudinal control model is non-linear and vulnerable to external environment factors. This paper designes a sliding mode controller to improve the control system’s robustness. What’s more, this fuzzy controller reduces the inherent chattering of the sliding mode control method by adjusting the parameters of the switch function instantaneity. Compare with the common sliding mode control method, this paper’s controller is more stable, for this paper’s controller decreases the frequency of the control system’s input effectively. Simulation results show that system tracks the desired speed accurately and rapidly, while the system has strong robustness to parameter perturbation and external disturbances.

speed tracking, sliding mode control, fuzzy switch function, fuzzy control, Simulink simulation

2016年9月9日,

2016年10月17日

陕西省国际合作重点项目(编号:2015KW-024);陕西省工业科技攻关计划项目(编号:2016GY-032)资助。

高嵩,男,教授,研究方向:智能控制、多传感器信息融合、计算机控制、自主智能体及复杂网络控制等。吕军锋,男,硕士研究生,研究方向:计算机测控技术。陈超波,男,副教授,研究方向:智能控制和计算机控制等。曹凯,男,讲师,研究方向:自主无人系统、传感器、智能控制等。

TP391

10.3969/j.issn.1672-9722.2017.03.006