阶次带分析法在柴油机齿轮啸叫中的应用

（上海柴油机股份有限公司，上海200438）

阶次带分析法在柴油机齿轮啸叫中的应用

贾亚涛

（上海柴油机股份有限公司，上海200438）

阐述了齿轮啸叫的原因、噪声信号的基本调制原理，并由边频带理论提出阶次带分析法。对某柴油机齿轮啸叫问题进行测试分析，确定产生啸叫的齿轮并通过改进齿轮热处理工艺和加工工艺等方案，最终解决啸叫问题。

柴油机齿轮啸叫阶次带边频带

1 前言

对于小型柴油机，一般发动机内部的齿轮较少，通常只关心可靠性方面的问题，很少关注到齿轮噪声方面的问题。但随着行业NVH水平的提高，发动机的齿轮噪声问题也突显出来，而啸叫是齿轮传动中最常见且最易引人厌烦的噪声。本文从阐述啸叫产生的机理、信号的调制原理入手，然后分析实际测试信号，找到产生啸叫的齿轮，制定改进方案，最终解决啸叫问题。

2 齿轮噪声信号调制原理

齿轮啸叫的激励源是齿轮间的传动误差。传动误差主要由静态传动误差和动态传动误差两部分组成。静态传动误差是实际生产出来的齿轮，在齿形和齿向上与图纸设计值之间的偏差。动态误差是当齿轮工作面承载时，齿轮会产生一定的形变，由此导致的传动误差。齿轮啸叫的特点，一是由工作齿轮产生；二是有明显的阶次特征，与齿数、转速等相关；三是当某些零件固有模态被激励后啸叫表现得更为明显。

齿轮噪声信号的调制现象中包含有很丰富的信息，比如啮合频率、倍频、其周围的边频等。通过解读这些信号，也可称为解调，可以快速找到齿轮传动中出现的问题，所以研究信号调制对齿轮故障诊断是非常有用的。对齿轮噪声信号调制可分为两种，幅值调制和频率调制。不论是幅值还是频率调制，都是有载波信号和调制信号组合而成。设载波信号和调制信号分别为

式中，A、B为振幅，fc为载波信号的频率，fz为调制信号的频率。

2.1 幅值调制

幅值调制是由于齿面载荷波动使振动幅值变化的现象。比较典型的例子是齿轮的偏心使齿轮啮合时一边紧一边松，从而产生载荷波动，使振幅按此规律周期性地变化。齿轮的加工误差及齿轮故障使齿轮在啮合中产生短暂的“加载”和“卸载”效应，也会产生幅值调制。幅值调制公式[1]：

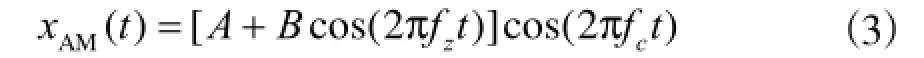
经傅立叶变换可得（取正频率部分）

式中，δ()为Dirac delta函数。上式中的频率成分为fc、fc+fz、fc-fz，它们是以fc为中心频率，以fz为间隔的对称调制边频带。

如图1所示，这两个信号，频率相对较高的称为载波，频率相对于载波频率来说较低的称为调制波。在齿轮信号中，啮合频率成分通常是载波成分，齿轮轴旋转频率成分通常是调制波成分。

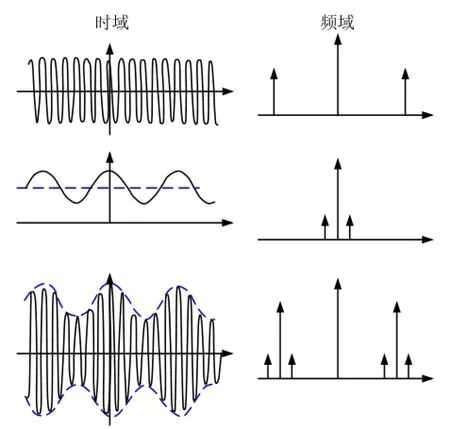
图1 单一频率的幅值调制

2.2 频率调制

齿轮载荷不均匀、齿距不均匀及故障造成的载荷波动，除了对振动幅值产生影响外，同时也必然产生扭矩波动，造成齿轮转速波动。这种波动表现在振动上即为频率调制（也可以认为是相位调制）。下面以频率调制为例进行论述。

频率调制公式为

同时，从绘画技法上对比，水彩《耕》（图13）更接近美术馆收藏李铁夫水彩作品中，有年款（或年代可考）的40、50年代的作品风格，这类作品用线条表现的更多，线条更拙（尤其1950年患病之后）。而与有30年代年款的作品面貌不太一致，对比来看，30年代作品多用大色块，水分足，用线相对少。

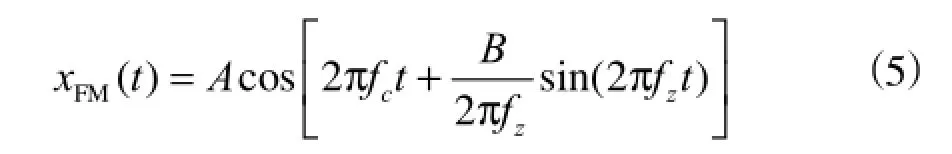
设mf＝B/(2πfz)，整理并展开成以贝塞尔函数为系数的三角函数级数

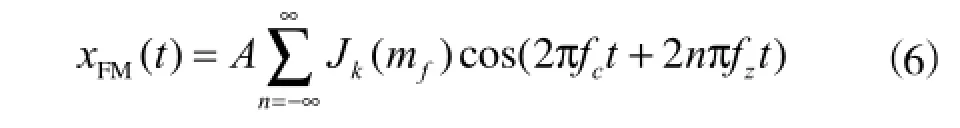
式中，n为整数，式（6）傅立叶变换可得（取正频率部分）

根据贝塞尔函数性质[2]可知，上式频率成分为fc、nfz，它们是fc为中心，以调制频率fz为间隔的无限多对调制边频带，见图2。

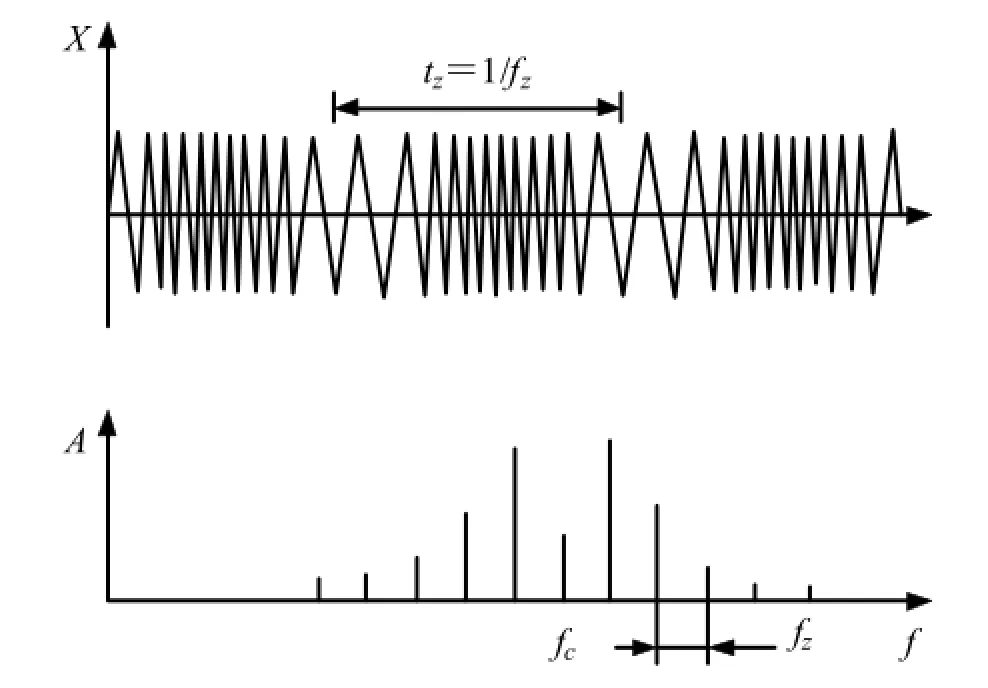
图2 频率调制及其边频带

由于幅值调制与频率调制的边频都相同,因此在频谱图中这两种调制的边频带是重叠的。对于同一频率的边带谱线,如果二者的相位相同,则它们的幅值相加，二者的相位相反时,则它们的幅值相减。所以载频谱线两侧的边频带的分布一般是不对称、不规则的。

3 阶次带分析

以上即为边频带的基本理论，但传统的边频带理论只适用于某一固定转速下的频谱数据分析。同时由于齿轮的噪声信号既有幅值调制又有频率调制，所以它的边频幅值会因相位不同而增大或减小，由此造成主频幅值可能会低于边频幅值，使主频和边频难以分辨。

所以为了更便捷而直观地将齿轮故障信号解调，可以将不同转速下的频域信号组合在一起，即将频率、幅值二维数据变为频率、转速、幅值三维数据，在单一转速下难以分清的主频、边频在这时就由阶次清晰地显示出来。也就是说，边频带理论通过以上修正，变为阶次带理论。

可简单定义如下，阶次带分析是通过读取阶次直接找到调制解调信号的一种方法。对齿轮来说，它是由啸叫齿轮的转动阶次在主动轮啮合阶次或其谐次周围形成阶次带。齿轮啮合阶次就是主阶次，即载波阶次，与主动轮齿数有关。阶次带的阶次差即啸叫齿轮的转动阶次，即调制阶次，则与传动比有关。

4 柴油机齿轮啸叫案例

某型柴油机的齿轮传动如图3所示，曲轴齿轮为主动齿轮，机油泵齿轮和真空泵齿轮为被动齿轮。曲轴齿轮齿数z1为44，机油泵齿轮齿数z2为35，真空泵齿轮齿数z3为31。

图3 齿轮传动图

载波频率为齿轮的啮合频率及其倍频，啮合频率计算公式为

式中，zi为齿数，fri为轴转动频率。调制频率为轴的转频，计算公式为

其中，n为发动机转速，r/min；z1/zi为传动比。以上为边频带理论分析时用到的几个基本公式。三个齿轮间的传动比如表1所示。

表1 齿轮传动比

应用阶次分析，对于曲轴齿轮，它的转速与发动机转速一致，即为1阶，由于曲轴齿轮为44齿，由它啮合产生的阶次即为44阶，也就是载波阶次。对于调制阶次，对不同的齿轮转速会有不同的调制阶次。由上表可知，如果调制阶次为1.26阶，则故障件为机油泵齿轮；如果调制阶次为1.42阶，则故障件为真空泵齿轮；以此类推。

4.2 测试数据及分析

图4为啸叫发动机的实测噪声频谱。测点位于发动机前端，正对曲轴中心线，距发动机前端表面100 mm，发动机转速为950～2 000 r/min，分析带宽0～4 000 Hz。将分析转速改为1 600～2 000 r/min，带宽改为1 100～1 600 Hz，图谱如图5所示。

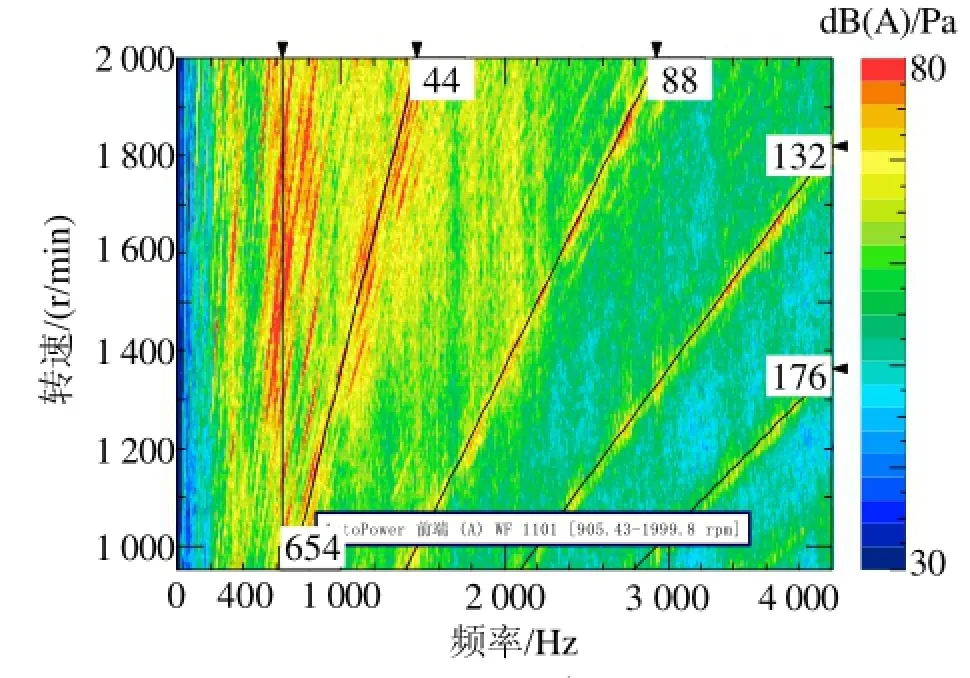
图4 发动机前端彩图

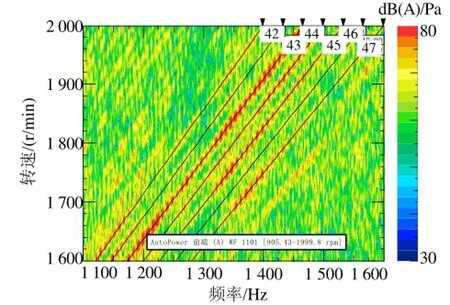
图5 发动机前端彩图局部放大

由图5可以明显地看出，存在一个以44阶为主阶次，以1阶为间隔的阶次带。由上面分析可知44阶为曲轴齿轮啮合阶次，即载波阶次，调制阶次为1阶，由曲轴齿轮故障引起。

用传统的边频带理论来分析，1 200 r/min时噪声频谱如图6所示：878.17 Hz对应发动机阶次为43.9阶，1791.06 Hz对应89.5阶，2665.38 Hz对应133.3阶，等等。与主阶次44阶、谐次88阶和132阶等有一定差异。所以直接从频谱图中找到故障主阶次比较困难和麻烦，相反从彩图中可以快速而准确地确认故障信号主阶次、谐次等。

4.3 改进方案及效果

曲轴齿轮改进方案设计，一是齿轮由剃齿后渗氮改为渗碳后磨齿，二是将齿轮精度提高一级。剃齿后渗氮改为渗碳后磨齿可有效减少热处理过程对齿轮外形的影响，配合对齿轮精度的提高，可有效降低齿轮啮合时的传动误差，降低啸叫风险。改进前后近场噪声对比如图7所示。由图中可见，改进后的44阶减弱，88阶、132阶基本消失，44阶附近的调制阶次已不太明显，主观感受无啸叫声。

图61 200 r/min时噪声频谱

5 结论

传统的边频带理论只能分析某一转速下的频谱数据，如果只监测某几个转速，得到的信息往往不全面。而阶次带分析可以避免这个问题，另外从三维图上可快速而直观地得到载波信号和调制信号的阶次及阶次差，更直观和便捷地找到问题原因。

图7 发动机前端彩图

[1]丁康.孔正国.振动调幅调频信号的调制边频带分析及其解调方法[J].振动与冲击，2005（6）.

[2]任怀宗，师先进.特殊函数及其应用[M].长沙：中南工业大学出版，1986.

Application of Order-band Analysis in Gear Whine Noise Diagnostic of Diesel Engine

Jia Yatao
（Shanghai Diesel Engine Co.,Ltd.,Shanghai 200438,China）

The reason of the gear whine is described,the basic modulation principle of the noise signal is given,and the order-band analysis method is proposed based on the sideband theory.The whine gear is identified through the analysis of order-band in the noise testing result of a certain diesel engine.The result shows the gear whine noise fulfills the requirements through improvement of the machining and heat treating of gear.

diesel engine,gear whine,order-band,sideband

10.3969/j.issn.1671-0614.2017.01.007

来稿日期：2016-09-12

贾亚涛（1983-），男，工程师，主要研究方向为柴油机振动噪声。