矩阵的秩和非零特征值个数的关系研究
朱 灿, 李 亦
(上海理工大学 理学院,上海 200093)
矩阵的秩和非零特征值个数的关系研究
朱 灿, 李 亦
(上海理工大学 理学院,上海 200093)
矩阵的秩和非零特征值个数是矩阵的重要不变量,研究二者关系也成为线性代数一个基本的问题.已有的文献分别给出了n阶矩阵的秩和非零特征值个数相等或相差n-1的充要条件.而矩阵指数又是矩阵的重要不变量,对复矩阵而言它指矩阵零特征值约当块的最大阶数.在已有文献基础上,研究了复数域上矩阵的秩和非零特征值个数二者的差与矩阵指数的关系,得到了矩阵的秩和非零特征值个数的差用矩阵指数刻画的一个充分必要条件,推广了已有文献的结果.
矩阵的秩; 特征值; 约当; 矩阵指数
1 问题的提出
矩阵的秩和非零特征值个数(重根按重数计,下同)是线性代数中的重要不变量.对非退化矩阵或实对称矩阵,这二者总是相等.但如果是矩阵的零特征值有阶数大于1的约当块,那么二者不相等.有很多学者研究了二者的关系.文献[1]给出了二者相等的等价刻画.文献[2]给出了二者的差为n-1的等价条件.这两种情形分别是二者差的上下确界.文献[3-6]讨论了二者的差为其他情形的刻画.而矩阵指数又是复矩阵的重要不变量,粗略地讲它是指矩阵的零特征值的约当块的最大阶数.矩阵指数在研究秩幂等矩阵中起着关键的作用,见文献[7-9].本文借助于矩阵的指数的概念,给出了矩阵的秩、非零特征值个数和矩阵指数三者差的上下确界以及矩阵的秩与非零特征值个数差的等价描述.
符号说明:
Mn()表示复数域上的n阶方阵全体.rank(A)和μ(A)分别表示矩阵A的秩和非零特征值个数.设A∈Mn()的约当标准型为diag(J1,J2,…,Jt,Jt+1,…,Js).其中,J1,…,Jt为零特征值对应的约当块,且它们的阶数分别为n1,…,nt,且满足n1≥…≥nt.Jt+1,…,Js为非零特征值对应的约当块.N(A)为线性方程组AX=0的解空间.
2 已有结论及相关准备
2.1 零特征值几何重数与矩阵的秩的关系
定理1[3]设A∈Mn()的秩为rank(A),其零特征值的几何重数为t,则rank(A)=n-t.
2.2rank(A)-μ(A)的上下确界
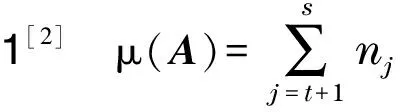
引理2[2]设A∈Mn(),则rank(A)-μ(A)=n0-t,其中n0=n1+n2+…+nt.
定理2[2]设A∈Mn(),则0≤rank(A)-μ(A)≤n-1.
2.3rank(A)=μ(A)的充要条件
已经知道rank(A)-μ(A)的上下确界:0≤rank(A)-μ(A)≤n-1,从而得知rank(A)和μ(A)未必总是相同.那么需要满足什么条件,才能使两者的差达到上下确界呢?首先回顾以下两个定理.
定理3[2]设A∈Mn(),则以下描述等价:
a.rank(A)=μ(A);
b.A没有形如xm(m≥2)的初等因子;
c.ind(A)≤1(ind(A)的定义见2.4);
d.rank(A)=rank(A2);
e. 对于任意自然数m(≥2),都有rank(A)=rank(Am);
f. N(A)=N(A2);
g. 对于任意自然数m(≥2),都有N(A)=N(Am).
定理4[2]设A∈Mn(),则以下描述等价:
a.rank(A)-μ(A)=n-1;
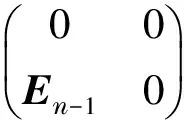
c.ind(A)=n;
d.An-1≠0;An=0;
e.rank(Al)=n-l,1≤l≤n-1且rank(Al)=0,0≤l;
f. N(A)⊂N(A2)⊂…⊂N(An-1)⊂N(An)(作为真子空间的包含);
g. 对于任意1≤k,l≤n,k≠l,则总有rank(Ak)≠rank(Al);
h. 对于任意1≤k,l≤n,k≠l,则总有N(Ak)≠N(Al).
2.4 矩阵的指数及相关引理
前文已知rank(A)-μ(A)的上下确界,即0≤rank(A)-μ(A)≤n-1,并给出了二者相等和相差n-1的等价刻画,那么是否二者的差还可能有其他情况呢?为了回答这个问题,本文借助于矩阵的指数ind(A)的概念.
设A∈Mn(),则可定义线性变换A:n→n,z→Az,Im(A)为线性变换A的象空间.
定义1[10]设A,A如上,定义Ind(A)=inf {k| Im(Ak)=Im(Ak+1)},ind(A)=inf {k| rank(Ak)=rank(Ak+1)}.
定理5Ind(A)=ind(A)=n1.

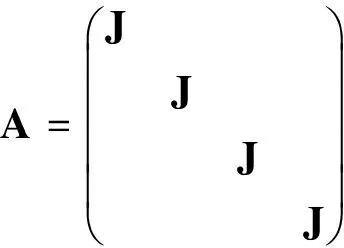
其次,取e1,e2,…,en为线性空间n的一组基,其中ei=(0,0,…,1,…,0)′(第i个分量为1).则线性变换A在这组基下的矩阵为A.令p=n1+…+nt,V1=span(ep+1,…,en).则V1为A-不变子空间,且A在V1上的限制在基ep+1,…,en下的矩阵为,记作J≠0.显然,矩阵J≠0非退化.记矩阵为J=0.而容易知道当k≥max{n1,n2,…,nt}=n1时,,所以Im(Ak)=V1=Im(Ak+1).接下来,考虑当k 定义2 设矩阵A如上,称n1为矩阵A的指数,记做ind(A). 由定理2rank(A)-μ(A)的上下确界已知,且有 b.rank(A)-μ(A)=n-1⟺ind(A)=n. 对非奇异矩阵,rank(A)=μ(A)且ind(A)=0,所以rank(A)-μ(A)=ind(A). 如果仅考虑奇异矩阵的情况,有以下总结: rank(A)-μ(A)=0⟺ind(A)=1; rank(A)-μ(A)=n-1⟺ind(A)=n. 因此,自然要问:对于奇异矩阵,是否恒有rank(A)-μ(A)=ind(A)-1?为此来看一个例子: rank(A)=2,μ(A)=0,ind(A)=2,不满足rank(A)-μ(A)=ind(A)-1. 定理6 rank(A)-μ(A)=ind(A)-1的充要条件是在矩阵A的约当标准型中,n2=n3=…=nt=1(即只有约当块J1可以是高阶的,其余零特征值对应的约当块均为一阶). 证明 由引理2,rank(A)-μ(A)=n1+n2+…+nt-t.从而有,rank(A)-μ(A)=ind(A)-1⟺n2+…+nt=t-1. 因为ni≥1,所以n2+…+nt≥t-1,且等号成立当且仅当n2=n3=…=nt=1. 所以rank(A)-μ(A)=ind(A)-1⟺n2=n3=…=nt=1,即J2,…,Jt均为1阶约当块.即A的约当标准型中,只有约当块J1可以是高阶的,其余零特征值对应的约当块均为一阶. 证明 由引理2可求得i=rank(A)-μ(A)-ind(A)=n2+…+nt-t. 先求最小值:因为ni≥1,所以n2+…+nt≥t-1,所以i=rank(A)-μ(A)-ind(A)≥-1,且只能在n2=n3=…=nt=1时可取到-1,所以mini=-1. 以下例子说明上确界可达,令 其中, 本文在参考文献[1-2]的基础上对复矩阵的秩与非零特征值个数的关系作了进一步的分析,完善和扩展了已有文献对矩阵的秩与非零特征值个数关系的研究.其主要结果概括如下:借助于矩阵指数的概念,给出了矩阵的秩、非零特征值个数和矩阵指数这三者差的取值范围以及上下确界,推广了已有文献仅对rank(A)-μ(A)=0和rank(A)-μ(A)=n-1的研究. [1] 张景晓.矩阵的秩与其非零特征值个数相等的条件[J].德州学院学报,2012,28(4):5-8. [2] 梁小春,陈梅香,杨忠鹏,等.矩阵的秩和非零特征值个数关系的进一步讨论[J].闽南师范大学学报(自然科学版),2014(2):1-6. [3] 钟成义,陈永生,朱德文.方阵零特征值代数重数与秩之间的关系[J].苏州科技学院学报(自然科学版),2008,25(2):29-31. [4] 于清江,包研科.用n阶方阵的迹判定其互异特征值的个数[J].大学数学,2006,22(5):157-159. [5] 林志兴,杨忠鹏,陈梅香.秩与非零特征值个数的差为3的矩阵[J].莆田学院学报,2015,22(2):1-4. [6] 吕洪斌,杨忠鹏,冯晓霞,等.矩阵的秩与非零特征值个数差的确定[J].吉林大学学报(理学版),2014,52(6):1210-1214. [7] 郭文静,杨忠鹏,陈梅香.(m,l)秩幂等矩阵和(m,l)幂等矩阵的特性研究[J].北华大学学报(自然科学版),2009,10(1):5-9. [8]BAKSALARYOM,TRENKLERG.Onk-potentmatrices[J].ElectronicJournalofLinearAlgebra,2013,26:446-470. [9]NIKUIEM,MIRNIAMK,MAHMOUDIY.SomeresultsabouttheindexofmatrixandDrazininverse[J].MathematicalSciencesQuarterlyJournal,2010,4(3):283-294. [10]BERNSTEINDS.Matrixmathematics:theory,facts,andformulas[M].2nded.Princeton:PrincetonUniversityPress,2009. (编辑:丁红艺) Discussions on the Relationship Between Ranks and Numbers of Non-zero Eigenvalues of Matrices ZHU Can, LI Yi (CollegeofScience,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China) The rank and the number of non-zero eigenvalues of a matrix are two important invariants and the relation between these two values is a basic problem in the linear algebra.Some authors have described the necessary and sufficient conditions for that the rank and the number of non-zero eigenvalues are equal or have a gap ofn-1.On the other side,the index of matrix is another important invariant,which,roughly speaking,is the maximal size of the zero eigenvalues in the canonical form of a complex matrix.Based on the existing research results,the relation of the gap between the rank and the number of non-zero eigenvalues with the index of matrix was investigated,and the necessary and sufficient conditions for these invariants were obtained,which is a generalization of some known results. rankofmatrix;eigenvalue;canonicalform;indexofmatrix 1007-6735(2017)01-0012-03 10.13255/j.cnki.jusst.2017.01.003 2016-07-22 上海理工大学教师教学发展研究项目(CFTD17016Z) 朱灿(1981-),男,博士研究生.研究方向:代数学.E-mail:czhu@usst.edu.cn O 151.21 A3 主要结果

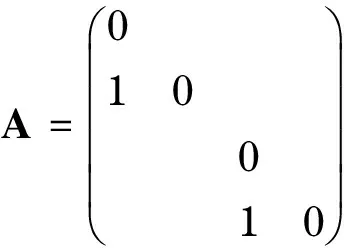
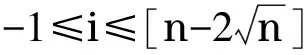
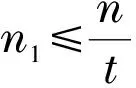
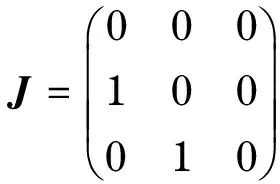
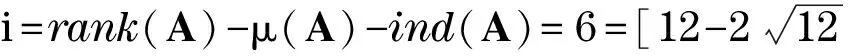
4 结 论

