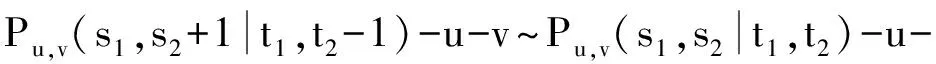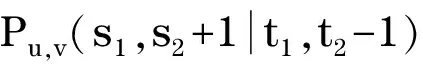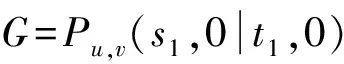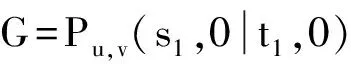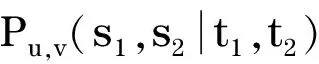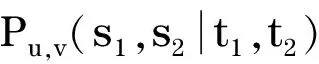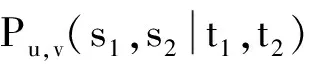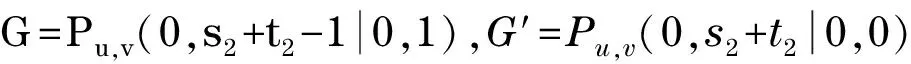拉手蜘蛛图的能量
雷 林, 何常香
(上海理工大学 理学院,上海 200093)
(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)
拉手蜘蛛图的能量
雷 林, 何常香
(上海理工大学 理学院,上海 200093)
图G的能量定义为其邻接矩阵的所有特征值的绝对值之和.拉手蜘蛛图定义为从K2的2个端点分别长出若干条悬挂边和长为2的悬挂路所得到的图.用ζn表示点数为n的所有拉手蜘蛛图构成的集合,通过拟序的方法,研究了拉手蜘蛛图的能量,并确定了ζn中能量最小的图.
图; 能量; 拟序; 蜘蛛图
1 基本概念及背景介绍
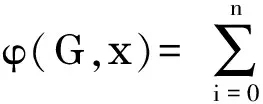
文献[7]中给出了多项式的拟序定义.
a. 若对所有的0≤i≤n,均有ai≤bi,则记f(x)⪯g(x);
b. 若f(x)⪯g(x)且f(x)≠g(x),则记f(x)g(x).
若存在i,j∈{0,1,2,…,n},使得ai
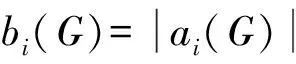
当G为二分图时,G的能量可写为[7]
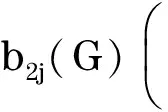
定义2[7]令G1和G2为n阶的二分图,
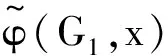
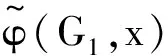
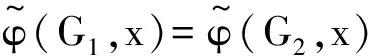
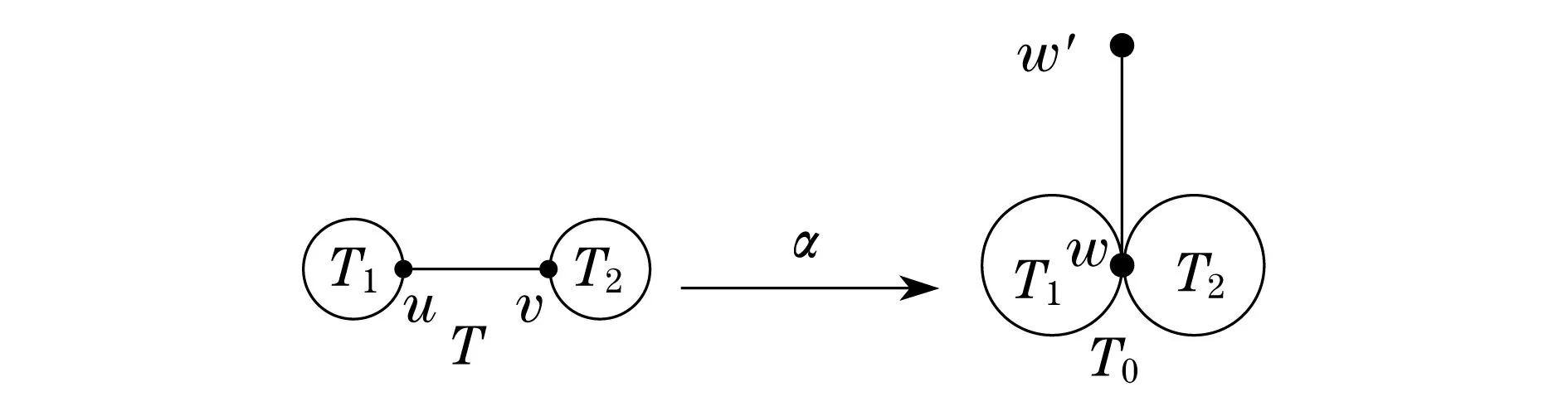
根据能量的积分公式,对于同阶的二分图G1和G2,由G1⪯G2可得E(G1)≤E(G2),由G1G2可得E(G1) 图 引理1[8]令u,v分别为图G,H的非孤立点(G·H为G与H的粘合),则有 a.φ(G·H,x)=φ(G,x)φ(H-v,x)+φ(G-u,x)φ(H,x)-xφ(G-u,x)φ(H-v,x); b. 若图G,H均为二分图,那么, 若u为二分图G中的非孤立点,用Gu(t1,t2)表示在u上添加t1条悬挂边和t2条长为2的悬挂路所得到的图. 推论1[8]令u为二分图G中的非孤立点,则 推论2 令u为二分图G中的非孤立点,则 证明 用H表示恰有1个公共端点的k条长为2的悬挂路所成的图,记公共点为v,则Gu(0,k)可以看成G和H在点u和v的粘连. 可直接计算出 所以 由引理1可得 推论3 令u为二分图G中的非孤立点,则 证明 令H=Gu(t1,0),由推论1可得 显然,Gu(t1,t2)=Hu(0,t2),由推论2可得 引理2[9](移星操作) 若图G为非平凡连通二分图,u,v为G上不同的两点,Gu,v(s,t)表示在u上添加s条悬挂边,在v上添加t条悬挂边所得到的图,令s,t,s′,t′均为非负整数,且s+t=s′+t′. 证明 根据推论2,有 令F=Gu(0,s),则G(u,v|s,t)=Fv(0,t),所以, 那么 由于s+t=s′+t′,s-s′=t′-t,所以,上述计算结果可简化为 引理4[4](缩边定理) 对任意的n阶树T,且T至少有1个非悬挂边,经α操作(如图2所示)后变为T0,则T≻T0且E(T)>E(T0). 图2 α操作 引理5[10]若v为单圈图或二分图的非孤立点,K1表示孤立点,那么,G≻(G-v)∪K1. 引理6[10]G,G′为单圈图或二分图,u,v,u′,v′分别为G,G′的割边. a. 若G-uv⪯G′-u′v′且G-u-v⪯G′-u′-v′,则G⪯G′; b. 若G-uvG′-u′v′或G-u-vG′-u′-v′,则GG′. 在研究拉手蜘蛛图的能量时,对于图3和图4中的两类确定图的能量需单独比较. 证明a. 当s1+t1=1,s2+t2=1时, 所以 图3 两类图(1) b. 当s1+t1≠1或s2+t2≠1时, 由引理4(缩边定理)可得 所以 图4 两类图(2) 证明 由图4可直接得到 在图u,v两点间移长为2的悬挂路,由引理3可得 同上,由引理3可得 综合式(1)和式(2),利用引理6的结论,即可证明引理8成立. 由推论2的计算式可得 证明 设s1≥t1. a. 当s1≥t1,s1-t1+1≥t2-s2时,由引理9可得 反复用引理9,则 b. 当s1≥t1,s1-t1+1 若s1>t1.因为,s1+s2+1 若s2=0,由引理8可得 结论得证. 证明 设s1≥t1,由定理1可得 综上可得 结论得证. [1]GUTMANI.Theenergyofagraph:oldandnewresults[M]∥BETTENA,KOHNERTA,LAUER.AlgebraicCombinatoricsandApplications.BerlinHeidelberg:Springer,2001. [2]GUTMANI,POLANSKYOE.Mathematicsconceptsinorganicchemistry[M].BerlinHeidelberg:Springer-Verlag,1986. [3]LIXL,SHIYT,GUTMANI.Graphenergy[M].NewYork:Springer,2012. [4]TIANT,YANWG,LISL.Ontheminimalenergyoftreeswithagivennumberofverticesofodddegree[J].MATCHCommunicationsinMathematicalandinComputerChemistry,2015,73(1):3-10. [5]RENQIANS,GEYP,HUOBF,etal.Onthetreewithdiameter4andmaximalenergy[J].AppliedMathematicsandComputation,2015,268:364-374. [6]HECX,WUBF,YUZS.Ontheenergyoftreeswithgivendominationnumber[J].MATCHCommuni-cationsinMathematicalandinComputerChemistry,2010,64(1):169-180. [7]SHANHY,SHAOJY,ZHANGL,etal.Anewmethodofcomparingtheenergiesofsubdivisionbipartitegraphs[J].MATCHCommunicationsinMathematicalandinComputerChemistry,2012,68(3):721-740. [8]SHANHY,SHAOJY.Theproofofaconjectureonthecomparisonoftheenergiesoftrees[J].JournalofMathematicalChemistry,2012,50(10):2637-2647. [9] 夏玲艳.图的变换对图的拟序和能量的影响及其应用[D].上海:同济大学,2015. [10]SHANHY,SHAOTY,GONGF,etal.Anedgegraftingtheoremontheenergyofunicyclicandbipartitegraphs[J].LinearAlgebraanditsApplications,2010,433(3):547-556. (编辑:石 瑛) Energy of the Hand-in-Hand Spider Graph LEI Lin, HE Changxiang The energy of a graphGis defined as the sum of absolute values of all eigenvalues of the graph.The hand-in-hand spider graph was obtained fromK2by adding some pendent edges and pendent paths of length 2 at its two end-vertices.The symbolζnwasusedtodenotethesetofhand-in-handspidergraphsofordern.By using the quasi-order of graph,the energy of the hand-in-hand spider graph was studied,and the graphs with the first smallest energies inζnweredetermined. graph;energy;quasi-order;spidergraph 1007-6735(2017)01-0007-05 10.13255/j.cnki.jusst.2017.01.002 2016-06-12 国家自然科学基金资助项目(11301340,11201303);上海市自然科学基金资助项目(12ZR1420300);沪江基金资助项目(B14005) 雷 林(1992-),女,硕士研究生.研究方向:代数图论.E-mail:1154375441@qq.com 何常香(1979-),女,副教授.研究方向:代数图论.E-mail:changxiang-he@163.com O 157.5 A (CollegeofScience,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)2 主要引理
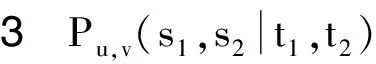

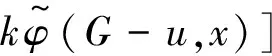
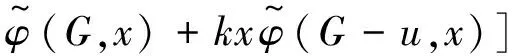
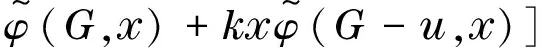
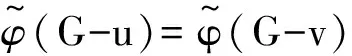
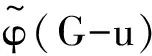

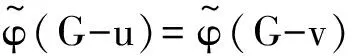
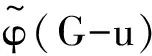
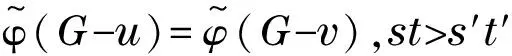


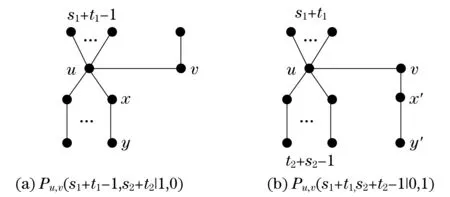



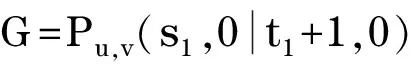
3 主要结论