基于双交叉和特征的快速分形图像编码研究

张 璟，张爱华，汪玮玮，唐婷婷

(南京邮电大学 理学院，江苏 南京 210023)

基于双交叉和特征的快速分形图像编码研究

张 璟，张爱华，汪玮玮，唐婷婷

(南京邮电大学 理学院，江苏 南京 210023)

针对传统基本分形编码存在的计算复杂性较高、编码时间较长的缺点，提出了一种基于双交叉和的特征值编码算法，以解决分形图像编码时间过长的问题。该算法通过构造图像块适当的特征向量，将“R在D集合中搜索MSE意义下的最佳匹配块”问题转换成“R的特征向量在D的特征向量空间中搜索最佳匹配块”的问题，将全局搜索转化为相对意义下的近邻搜索，使得匹配搜索只在初始匹配块的邻域内进行，有效地减少了搜索对象，从而进一步加快了编码速度。采用图像方块分割进行了多种算法的对比仿真实验，实验结果表明相对于其他算法，所提出的算法在保证一定重建图像质量的前提下，提高了图像的结构相似度，图像编码时间明显缩短，较好地实现了提高算法编码速度的目的。

分形；分形图像编码；特征向量法；双交叉和特征

0 引 言

当今信息时代，人们在面对大量图像信息数据时，如何进行高效率的存储和传输，成为了一个重要问题。而对于提高存储和传输的效率，不仅仅只依赖硬件设备自身的更新换代，也需要高性能图像压缩技术的研究予以支持。分形几何[1]作为新兴数学的一个分支，对描述自然界中那些不规则的几何形状提供了帮助，在图像编码邻域也得到了广泛的应用。

基于分形的图像压缩编码[2]方法是一种新的编码方法，它是利用图像的自相似性以及比例特性，通过消除图像的几何冗余度来实现图像数据的压缩。在分形编码中，一幅图像由一组使它近似不变的压缩仿射变换来表示，重构图像是压缩变换的不动点，压缩仿射变换的参数组成原始图像的分形码。相对来说，这是一种简单的快速迭代过程，解码图像由解码表示的压缩变换迭代作用于任意初始图像来逼近[3]。

分形图像压缩编码的主要特点是：在获得高压缩比的同时还能够保持较好的解码图像质量，运算速度与提高图像分辨率的关系不大，选择合适的分形模型可以构造出较清晰的边缘细节，解码过程快捷，等等。但与此同时，其计算复杂性较高、编码时间较长的缺点也尤为显著，已经严重影响到了分形编码的广泛应用[4]。因此在保证图像质量不变或更好的前提下，如何加快编码也是分形编码的一个重要课题。而基于特征向量法的快速分形编码算法就实现了这一目标，通过构造图像块适当的特征向量，将全局搜索转化为相对意义下的近邻搜索，减少了搜索对象，从而加快了编码速度。

文中所依据的特征向量法是Saupe提出的一种快速分形编码方法[5]，约定码本Ω中的码本块都按某种方式向量化，即D∈Ω表示线性空间Rn中的向量(n=N×N,N×N是码本块D的尺寸)。它首先构造图像块X块(R块和D块)的特征向量φ(X)，然后证明极小化MSE(R,D)的问题等价于极小化Δ(R,D)的问题：

Δ(R,D)≜min(d(φ(R),φ(D)),d(-φ(R), φ(D)))

(1)

其中，d是欧氏距离。

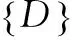
d(FR,FD)≤δ⟺MSE(R,D)≤ε

(2)

其中，FX为图像块X的特征向量；δ>0、ε>0为适当阈值。

所以，如何选取特征向量以及在特征向量空间中的搜索方法是特征向量法的关键。

文中选取规范化图像子块水平、垂直中位线，以及两条对角线所在直线构成的双交叉上像素点的灰度值作为特征点，以这些特征点的归一化值的绝对值之和来定义图像规范块双交叉和的特征；先在理论上证明了双交叉和与均方误差的关系不等式，再对码本Ω中的码本块按照每一块双交叉和的大小进行排序，在编码每一R块时，使用二分法在赋序码本中找出其初始匹配块，之后的匹配搜索便直接在初始匹配块的邻域内进行[7-8]。

1 算 法

1.1 算法理论依据

首先给出双交叉和特征的定义：

定义1：设子块X=(xi,j)∈RN×N，X的规范化为：

(3)

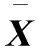
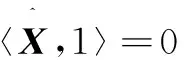
S(x)=

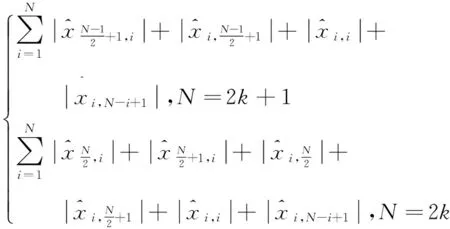
(4)

即双交叉和为规范块垂直水平交叉线和对角线(构成形如“×”“+”形状的两个交叉的结构)上每个像素点灰度值的绝对值之和。

理论基础为下述定理，参考并给出证明：

定理1：设R,D∈RN×N,则有下面的不等式成立：

(5)

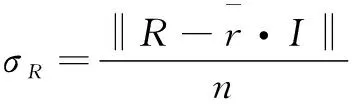
(6)

有：

(7)

由柯西不等式：

(8)

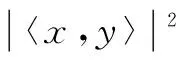
(9)

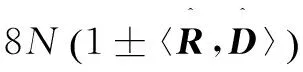
(10)

而约束条件为：

(11)

证毕。

1.2 算法分析与实现

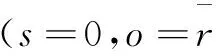
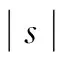
显然，N(Dinit,k)⊂Ωη⊂Ω。搜索空间由全局搜索变为局部搜索，编码时间会随着搜索空间的缩小而减少，从而加快编码速度。对于不同的k值，编码加速的程度有所不同[13-14]。

2 仿真实验及结果分析

文中图像采用方块分割，仿真使用的图像是256×256，8bit量化的Lena图像。选取R块大小为8×8，D块大小为16×16，步长σ=16。操作平台为运行Windows7的IntelPentium(2.00GHzCPU/2.00G内存)PC，仿真程序使用MATLABr2012b编写，测试参数为编码时间(s)、峰值信噪比(PSNR)(dB)和结构相似度(FSIM)[15]。

通过实验将文中算法与基本算法以及1-范数算法[16]的编码性能进行比较：双交叉和特征算法的编码时间与解码图像质量跟R块的分类阈值τ，容许码本阈值参数η，搜索邻域半径大小k有关。根据文献[9]，对于参数τ和η，固定其取值，默认τ=4，η=3。根据Lena图像的实验数据，三种算法比较结果见表1。

搜索邻域半径K取不同值时，三种算法的实验效果如图1～3所示。

表1 基本分形算法、1-范数算法与文中算法对比结果

从表中数据分析可得，双交叉和特征算法与基本分形算法及1-范数算法相比，从主观上看，基于双交叉和特征算法基本上不改变重构图像的质量；从客观上看，相比于1-范数算法，文中算法在略微提高性噪比的基础上，大幅减少了运算时间，且提高了结构相似度，与基本分形算法相比，该算法并没有降低太多信噪比，且编码速度比之快了6倍，结构相似度也显著提高。综上所述，文中算法可以在保证一定图像质量的前提下，大幅提高编码速度和结构相似度。

图1 k=1的实验结果图

图2 k=2的实验结果图

图3 k=3的实验结果图

3 结束语

由于传统基本分形编码有着计算复杂性较高、编码时间较长的缺点，依据特征向量法提出了一种基于双交叉和特征向量的改进方法。通过寻找最佳匹配块的方式，在不影响图像质量的前提下，缩短了图像编码时间，实现了编码速度的提升，并提高了图像的结构相似度。而且文中算法引进了参数搜索邻域半径k，可以针对不同场合的需要来选择合适的k值，有较强的灵活性和实用性。

实验结果表明，该算法相对于基本分形算法，编码效率更高，应用前景更加广阔。

[1] 法尔科内.分形几何-数学基础及其应用[M].第2版.北京:人民邮电出版社,2007.

[2]GalabovM.Fractalimagecompression[C]//Proceedingsofthe4thinternationalconferenceoncomputersystemsandtechnologies:e-learning.[s.l.]:ACM,2003:347-361.

[3] 齐利敏,刘文耀,吕大伟.基于分形的快速压缩编码方法[J].西安电子科技大学学报:自然科学版,2008,35(2):373-376.

[4] 冯 晔,冯忠义,朱幼莲,等.分形编码技术的介绍与展望[J].常州技术师范学院学报,1999,5(2):1-6.

[5] 何传江,蒋海军,黄席樾.快速分形图像编码的一种特征方法[J].电子学报,2004,32(11):1864-1867.

[6]WohlbergB,JagerGD.Areviewofthefractalimagecodingliterature[J].IEEETransactionsonImageProcessingAPublicationoftheIEEESignalProcessingSociety,1999,8(12):1716-1729.

[7] 何传江,申小娜.改进分形图像编码的叉迹算法[J].计算机学报,2007,30(12):2156-2163.

[8]LaiCM,LamKM,SinWC.Improvedsearchingschemeforfractalimagecoding[J].ElectronicsLetters,2002,38(25):1653-1654.

[9] 何传江,黄席樾.基于图像块叉迹的快速分形图像编码算法[J].计算机学报,2005,28(10):1753-1758.

[10]LeeCK,LeeWK.Fastfractalimageblockcodingbasedonlocalvariances[J].IEEETransactionsonImageProcessingAPublicationoftheIEEESignalProcessingSociety,1998,7(6):888-891.

[11]HartensteinH,SaupeD.LosslessaccelerationoffractalimageencodingviathefastFouriertransform[J].SignalProcessingImageCommunication,2010,16(4):383-394.

[12] 袁宗文,鲁业频,杨汉生.半叉迹特征的快速分形图像编码[J].计算机工程与应用,2016,52(3):197-201.

[13] 李高平,杨 军,陈毅红.改进转动惯量特征的快速分形图像编码算法[J].计算机工程与应用,2013,49(24):144-148.

[14] 张思思,刘 宇,赵志滨,等.一种基于相邻匹配的分形图像检索算法[J].计算机科学,2015,42(12):292-296.

[15]ZhangLin,ZhangLei,MouXuanqin.FSIM:afeaturesimilarityindexofimagequalityassessment[J].IEEETransactionsonImageProcessing,2011,20(8):2378-2386.

[16]HeC,YangSX,XuX.Fastfractalimagecompressionbasedonone-normofnormalizedblock[J].ElectronicsLetters,2004,40(17):1052-1053.

Investigation on Fast Fractal Image Encoding with Sum of Double Cross Eigenvalues

ZHANG Jing,ZHANG Ai-hua,WANG Wei-wei,TANG Ting-ting

(School of Science,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)

For the shortcomings of high computational complexity and long encoding time of the traditional fractal coding,an encoding algorithm based on the sum of double cross eigenvalues is proposed in order to solve the problem of long encoding time.The problem,RsearchforthebestmatchingblockofMSEsenseintheDset,isconvertedintoanotherone,theeigenvectorofRsearchforthebestmatchingblockofDintheeigenvectorspace.Thus,globalsearchistransformedintoneighborsearchbyconstructingsuitablefeaturevectorfortheimageblockintheoppositesenseandmatchingsearchiscarriedoutonlyinthefieldoftheinitialmatchingblock,whichreducessearchobjectsandthenspeedsupencoding.Throughcomparativesimulationexperiment,avarietyofalgorithmsarecomparedandsimulatedbyusingimagesegmentation.Theresultsofexperimentsshowthatthealgorithmpresentedhasimprovedthefeaturesimilarityandreducestheimageencodingtimemoreeffectivelyunderthepremiseofensuringqualityofthereconstructedimage,andthatthepurposeofimprovingtheencodingspeedprocedurehasbeenachieved.

fractal;fractal image coding;eigenvector method;sum of double cross eigenvalues

2016-04-21

2016-08-10

时间：2017-02-17

国家自然科学基金面上项目(11471114,61372125)

张 璟(1991-)，男，硕士研究生，研究方向为非线性分析及应用；张爱华，教授，硕士生导师，研究方向为非线性分析。

http://www.cnki.net/kcms/detail/61.1450.TP.20170217.1628.032.html

TP

A

1673-629X(2017)03-0159-04

10.3969/j.issn.1673-629X.2017.03.033