环扩张与(d,n)-余挠模及(d,n)-平坦模

武 斌

(兰州资源环境职业技术学院基础学科部，甘肃兰州 730070)

环扩张与(d,n)-余挠模及(d,n)-平坦模

武 斌

(兰州资源环境职业技术学院基础学科部，甘肃兰州 730070)

设R是环，本文讨论了(d,n)-余挠模与(d,n)-平坦模在分式环上的若干性质，并给出了这两类模在Morita等价环上的等价刻画。

(d,n)-余挠模；(d,n)-平坦模；分式环；Morita等价环

1 引言

本文中，所有的环是指有单位元的结合环，模指酉模.

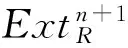
分式环是环的一类重要扩张.本文讨论了(d,n)-余挠模与(d,n)-平坦模在分式环上的若干性质.Morita等价环及该环上模的性质被人们广泛研究.2007年，Su[3]在Morita等价的环上对模的Gorenstein投射维数与内射维数进行了讨论得出：若环R≈S，则GpdRM=GpdSF(M),GidRM=GidSF(M).2012年，Yang[4]研究了Gorenstein同调维数在Morita等价的环上发生的变化.本文给出了(d,n)-余挠模与(d,n)-平坦模在Morita等价环上的等价刻画，证明了：若R≈S，M是(d,n)-余挠右R-模当且仅当F(M)是(d,n)-余挠右S-模；N是(d,n)-平坦右R-模当且仅当F(N)是(d,n)-平坦右S-模.其中，所涉及的其它专业名词和术语均来自于文献[5-8].

2 环扩张与(d,n)-余挠模及(d,n)-平坦模

设··R是交换环.如果1R∈S，且S关于R的乘法是封闭的，则称环R的子集S是乘法闭的.设S是R的乘法闭子集.在R×S上定义关系～如下：对任何(a,s),(b,t)∈R×S，(a,s)～(b,t)当且仅当存在u∈S使得u(at-bs)=0.则～是R×S上的等价关系.令S-1R=(R×S)/～={a/s|a∈R,s∈S}.在S-1R上定义加法与乘法为：a/s+b/t=(at+bs)/st，(a/s)(b/t)=ab/st.则S-1R关于上面的加法和乘法构成环.设M∈Mod-R，在M×S上定义关系～如下：对任何(x,s),(y,t)∈M×S，(x,s)～(y,t)当且仅当存在u∈S使得u(xt-ys)=0.

故～是M×S上的等价关系.令S-1M=(M×S)/～={x/s|x∈R,s∈S}，则S-1M关于运算x/s+y/t=(xt+ys)/st，(x/s)(y/t)=xy/st作成S-1R模，且S-1M≅MR⊗S-1R.

引理1 设R是交换环，S是R的乘法闭子集.如果S-1R是投射R-模.则任意(d,n)-余挠S-1R-模是(d,n)-余挠R-模.

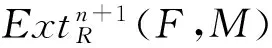
定理1 设R是交换环，S是R的乘法闭子集.如果S-1R是投射R-模，则对任意(d,n)-平坦R-模N，S-1N是(d,n)-平坦S-1R-模.

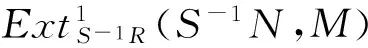
定理2 设R是交换环，S是R的乘法闭子集.如果S-1R是投射R-模，则对任意(d,n)-余挠R-模M，HomR(S-1R,M)是(d,n)-余挠S-1R-模.

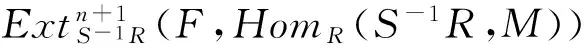
3 Morita等价环与(d,n)-余挠模及(d,n)-平坦模

定理3 设R和S是等价环，F:Mod-R→Mod-S和G:Mod-S→Mod-R是等价函子，则以下结论成立：(1)M是(d,n)-余挠右R-模当且仅当F(M)是(d,n)-余挠右S-模；(2)N是(d,n)-平坦右R-模当且仅当F(N)是(d,n)-平坦右S-模.

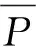
(充分性)由G(F(M))≅M得证.

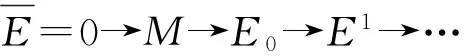
(充分性)由G(F(N))≅N得证.

推论1 设R是环，e∈R是非零幂等元，如果ReR=R则有：(1)对任何右R-模M,M是(d,n)-余挠右R-模当且仅当M⊗RRe是(d,n)-余挠右eRe-模；(2)对任何右eRe-模M，M是(d,n)-余挠右eRe-模当且仅当M⊗eReeR是(d,n)-余挠右R-模；(3)对任何右R-模N，N是(d,n)-平坦右R-模当且仅当M⊗RRe是(d,n)-平坦右eRe-模；(4)对任何右eRe-模N，N是(d,n)-平坦右eRe-模当且仅当M⊗eReeR是(d,n)-平坦右R-模.

推论2 设R是环，n≥1是自然数，则有：(1)对任何右R-模M,M是(d,n)-余挠右R-模当且仅当M⊗RMn(R)eii是(d,n)-余挠右Mn(R)-模；(2)对任何右Mn(R)-模M，M是(d,n)-余挠右Mn(R)-模当且仅当M⊗Mn(R)eiiMn(R)是(d,n)-余挠右R-模；(3)对任何右R-模N，N是(d,n)-平坦右R-模当且仅当M⊗RMn(R)eii是(d,n)-平坦右Mn(R)-模；(4)对任何右Mn(R)-模N，N是(d,n)-平坦右Mn(R)-模当且仅当M⊗Mn(R)eiiMn(R)是(d,n)-平坦右R-模.

[1]MAO Lixin,DING Nanqing.Relative cotorsion modules and relative flat modules[J].Communications in Algebra, 2006(6):2303-2317.

[2]WU Bin.(d,n)-Cotorsion modules and (d,n)-flat modules[D].兰州：西北师范大学，2008.

[3]宿维军. Morita等价环上Gorenstein 投射维数与内射维数[J].聊城大学学报：自然科学版, 2007(3):109-111.

[4]TANG Xiaoyan.Gorenstein homological dimensions and change of rings[J].Journal of Mathematical Research with Applications,2012(5):571-581.

[5]Enochs E E,Jenda O M G.Relative homological algebra[M].Berlin:de Grugter,2000.

[6]Osborne M S.Basic homological algebra[M].New York:Spring-Verlag,2003.

[7]Rotman J J.An introduction homological algebra[M].New York:Academic Press,1979.

[8]TONG Wentin.An introduction to homological algebra[M].Beijing:High Education,1998.

The Extension of Rings and (d,n)-cotorsion Modules and (d,n)-flat Modules

WU Bin

(Department of Basic Courses,Lanzhou Resources Environment College,Lanzhou Gansu 730070,China)

LetRbe any rings.The property of (d,n)-cotorsion modules and (d,n)-flat modules on rings of quotients are investigated, the equivalent descriptions of these modules on Morita Equivalence rings are given.

(d,n)-cotorsion module; (d,n)-flat module; rings of quotients; Morita Equivalence rings

2016-08-13

兰州资源环境职业技术学院自然科学基金资助项目“基于(d,n)-余挠模及(d,n)-平坦模的研究”(Z2015-11)。

武 斌(1982- )，女，讲师，硕士，从事环的同调理论研究。

O153.3

A

2095-7602(2017)02-0008-03