好问题成就好课堂

文︳周慧芳

好问题成就好课堂

文︳周慧芳

某教师教学“认识角”时，为了让学生感知数学与生活的联系，配合设计的“我们去旅游”的情境线索，出示了一系列与交通标志相关的实物：出口指示牌（长方形），转弯指示牌（三角形），限速警示牌（圆形）等，让学生比较它们的不同（长方形、三角形都有角，而圆形没有角）。接着师生之间有了如下的对话——

师：这些是什么？

生：交通标志。

师：它们有什么不同？

生1：有些是圆的，有些是方的。

师：还有吗？

生2：它们表示的意义不同。

师：什么不同？

生2：转弯指示牌表示……，限速警示牌表示……

生3：我不同意……

学生争论起来。

在这种满堂问的课堂里，教学气氛是活跃了，但时间浪费了，新知却未呈现，教学效果自然不好。一些教师总是想让学生体会数学与生活的联系，千方百计创设情境，引出问题，结果抛出了一些与教学内容无关的问题。案例中，当生1已经讲到“要害”时，教师的那句“还有吗？”本是想让更多的学生来叙述，提高课堂的参与度，未料这一发问是画蛇添足。可见，教师的提问如果没有明确的目的，就不能发挥相应的作用。教师的问提得好，学生才不会偏离思维方向，课堂才会精彩。

课始问应该明确教学内容和方向。上述案例中教师之所以失败，正是因为提问没有明确的目的，随意提问。本堂课的教学内容是角的认识，教师在出示图片后，提问应该直指数学图形——角。这样学生的回答才不会天马行空，不知所云。

课中问应有利于突破难点。数学教材每章节都有重难点，教学中处理重难点时，教师的提问应该有利于学生突破重难点，使复杂问题简单化，让学生迅速掌握新知。

如，上“圆”的练习课时，教师出示：一个圆的半径扩大3倍，它的直径扩大（）倍，周长扩大（）倍，面积扩大（）倍。

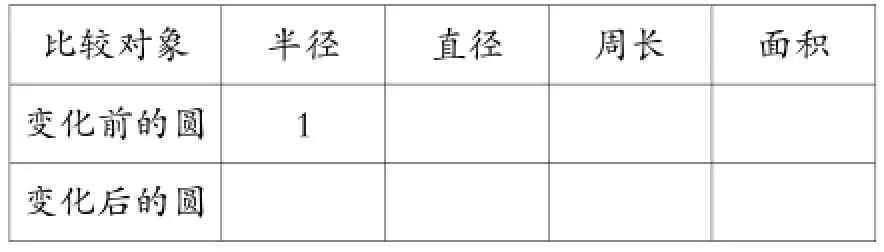
比较对象半径直径周长面积变化前的圆1变化后的圆

然后提问：假设圆的半径是1厘米，你能完成表格的填写吗？如果一个圆的半径扩大4倍，它的直径、周长、面积会怎么变化？如果圆的直径扩大5倍，你能想到什么？如果圆的周长扩大a倍呢？

由于习题中没有具体的数据，学生思考时找不到解决问题的突破口。于是教师在难点处层层设问，步步引导。学生最终找到突破口，顺利解决了问题。

课尾问应画龙点睛。课堂小结在课堂教学中往往起着提纲挈领、画龙点睛的作用。教师在结尾处可以提出本节课还没有完全解决的问题，或者提出与本节课相关的后续性问题，或者提出与下节课学习相关的前瞻性问题，让学生带着问题，进行下一步的学习。

如，一位教师上“同类项”这一节，在课后小结时，先举了一个例子：“上一节课我们学习了降幂排列，如果说降幂排列好比是同学们按照个子高低排队，那么今天学习的同类项可以比作什么？”学生们立即开展了讨论，小结时发言异常踊跃：“同类项好比是按照男生、女生来排队。”“同类项好比是卖水果时橘子归一类，香蕉归一类，苹果归一类。”教师追问：“那么同类项的分类应该注意些什么呢？”我想学生们一定会对同类项的分类留下深刻的印象。

（作者单位：永州市零陵区徐家井小学）