中值直方图在线列扫描系统中的应用

周 妮，张承宏，李范鸣



中值直方图在线列扫描系统中的应用

周 妮，张承宏，李范鸣

（中国科学院上海技术物理研究所，上海 200083）

针对红外线列扫描系统所特有的垂直于扫描方向的条状噪声，本文采用Tendero所提出的基于中值直方图均衡的校正算法对其进行非均匀性校正。并且在计算中值直方图时，采用IQR加权算子来弥补采用高斯加权算子时所导致的过度平滑问题。实验表明，本算法简单快捷，易于工程实现，不仅可避免一般场景法存在的“鬼影”问题，而且具有较好的图像视觉质量。

红外线列扫描系统；中值直方图均衡；场景法；IQR滤波

0 引言

众所周知，红外成像系统以其全天候、全天时工作等优点，被广泛地应用于工业、医学、军事等领域。然而由于制作工艺、材料配比等问题[1]，在相同的辐射亮度下，红外成像系统的每个探测单元的响应曲线各不相同；这种响应曲线的差异被称为固定模式噪声（FPN）或非均匀性（NU）。它严重影响了成像质量，从而降低了基于红外成像的搜索跟踪系统的探测距离等方面的性能。所以为了修正红外成像系统的非均匀性（NU），需要对其进行非均匀性校正（NUC）。并且由于红外成像系统的非均匀性（NU）会随时间的增加而增加，还需要每隔一段时间重复对其进行非均匀性校正（NUC）。修正红外成像系统的非均匀性（NU），主要有两类校正算法：定标法和场景法。

定标法假定当红外成像系统观测均匀的辐射源时，其输出的图像也应该是均匀的，然后根据参考文献[1]中所描述的探测单元的线性模型就可以进行非均匀性校正（NUC）。定标法主要有一点校正，两点校正和多点校正[2]；其中最常用的方法为两点校正法。它采用两个温度的均匀黑体作为辐射源，然后对于×的红外探测器，根据以下公式来计算出每个探测单元的增益和偏置：

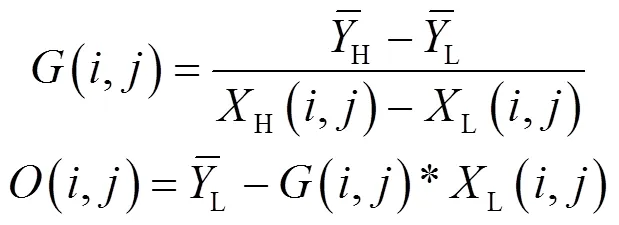
定标法操作简单，可获得较高的温度分辨率，但是需要额外的辅助设备（黑体或挡板等机械结构），并且需要专门的校正时间。

而场景法不受此限制，它利用场景的运动来估算探测单元的参数或恢复理想的场景，并以此来进行非均匀校正。Torres[3]采用卡尔曼滤波来进行基于场景的校正；Cain[4]结合贝叶斯函数和最大相似算法来进行基于场景的校正；还有时域高通滤波法[5]，恒定统计法[6]，神经网络法[7]等基于场景的校正算法。这些算法都基于如下假设：

如果所有探测单元能看到相同的场景，它们应该具有相同的均值和标准差，即：

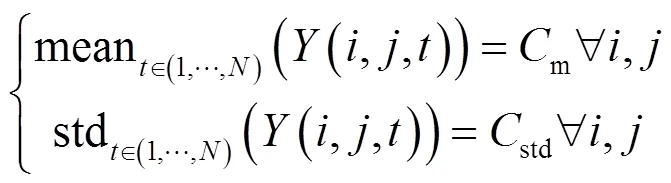
式中：为帧数；为某个时刻；,为每个探测单元的位置；m和std为一个常数。从公式(2)中可以看出的长度的确定十分重要：①校正的场景必须足够随机（不能是静止场景），以保证各点的统计量是相等的；②图像的累积时间足够长，计算出的统计量具有足够的精度和置信度。

在场景法中会引入“鬼影”现象，对此许多文献[8-11]提出了去除方法，然而这些算法普遍计算比较复杂，容易受场景随机噪声的影响。

为此，Tendero提出了基于中值直方图均衡的场景校正算法[12]；这种算法所需帧数少，运算简单，可有效解决“鬼影”现象；尤其适合1维（行或列方向）非均匀性的校正。

红外线列扫描系统以其成本低，扫描视场大（可实现360°全方位或全俯仰扫描）等优点，被广泛应用于地面预警系统中。由于其特有的扫描特性，其非均匀性表现为垂直于扫描方向的条状噪声，即1维非均匀性。因此，本文采用Tendero所提出的基于中值直方图均衡的校正算法来进行非均匀性校正。实验结果表明这种算法可有效去除红外扫描系统的条状噪声，取得了非常好的效果。

1 算法描述

1.1 场景法的原理

由文献[1]中可知，每个探测单元的响应可用线性模型来描述：

Y()＝g()×X()＋o() (3)

式中：g()和o()分别为每个探测单元的增益和偏置；X()为输入到探测单元的辐射强度。Tendero假设每个探测单元的在一定时间内的直方图为常数，即：

hist∈(1,…, N)((,,))＝hist",(4)

式中：为帧数；为某个时刻；,为每个探测单元的位置；从式中可以看出只要求出hist就可以得到校正所需的增益和偏置参数。

1.2 中值直方图均衡

中值直方图均衡算法最初由Delon提出[13]，它主要用来对不同相机观测同一场景时产生的增益差进行校正，以便更好地比较两个相机拍摄的图像。后来被应用于修正视频图像帧间对比度和亮度的快速变化[14]。本文利用中值直方图均衡来进行线列扫描系统的非均匀性校正（NUC）。下面先回顾一下中值直方图均衡的基本原理。

假设幅图像的累积直方图分别为1,2, …,H，那么其均衡后的图像累积直方图，即中值累积直方图如下式所示：

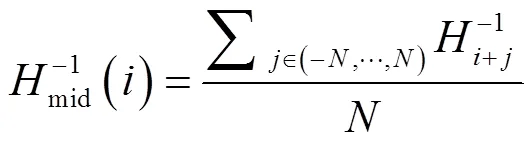
式中：i为每个像素；N为计算中值直方图的帧数。当计算出它们的中值累积直方图后就可以得出这些图像均衡后的中值直方图Hmid，然后通过对所有图像以中值直方图Hmid进行映射，就可以修正这些图像间对比度和亮度的变化。图1为两幅图像的中值直方图示意图。

1.3 基于中值直方图均衡的非均匀校正算法

由于线列扫描系统是通过扫描成像的，其非均匀性体现为扫描方向上的条状噪声，如图2所示。

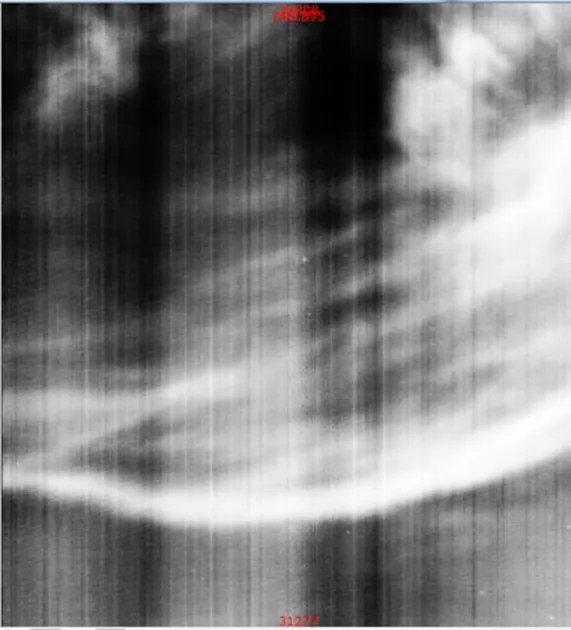
图2 线列扫描系统的条状噪声

图2为从上至下扫描，所有其非均匀性表现为竖状条纹。与文献[12]中一样，我们可以假定相邻像元在扫描过程中看到的场景在一段时间内几乎一样，而相邻像元间对比度和亮度的变化是由其非均匀性所引起的；也就是说它们在时域（扫描方向）上的直方图基本一致，这样我们就可以应用中值直方图均衡来进行基于场景的非均匀性校正。

首先，计算每个像元在时域（扫描方向）上的累积直方图H；然后根据公式(5)，取大小为的滑动窗口来计算窗口内像元的累积直方图H，计算其中值累积直方图：

在参考文献[12]中，Tendero采用高斯加权算子来进行中值累积直方图的计算。但是在线列扫描系统中这种加权算子的效果并不是很好；参考文献[15]中提出的IQR（Interquartile range）滤波能很好地去除高斯分布中的杂散噪声，因此本文采用IQR加权算子来进行中值累积直方图的计算。IQR滤波公式如下：

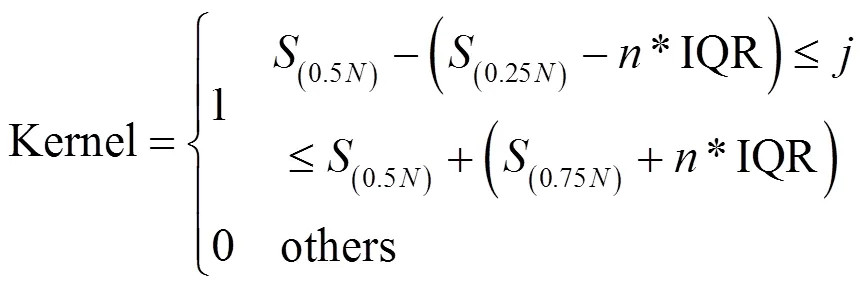
IQR＝0.7413*((0.75N)－(0.25N)) (8)

式中：(0.5N)，(0.25N)，(0.75N)分别为长度为的数据的中位数，第一四分位数和第三四分位数；为一个常数。

最后，把每个像元经过中值直方图均衡后的结果，即每个像元的理想场景作为应变量，每个像元的原始值为自变量，通过多项式拟合，就可以求出每个探测单元的增益和偏置系数；然后根据公式(3)就可输出校正后的图像。

2 实验结果

实验所需数据由本所自行研制的摆扫型红外告警系统所提供。这个系统由一个长波576×6的红外线列探测器，一个可进行±20°往返扫描的摆镜，一个可360°旋转的方位转台以及相关光学和电路组成。它可在方位0～360°，俯仰0～80°的搜索范围内进行红外目标的探测捕获。每列的扫描周期为40ms；摆镜完成一次往返扫描的周期为0.6s。

算法采用VC6.0＋＋编写，计算中值直方图所需的窗口大小＝8；方向为摆镜的扫描方向，图3～图5显示了扫描620列的校正前后的效果。

从图3中可以看出，由于采用俯仰方向上下扫描，原始图像的非均匀性呈现为竖状条纹噪声。图4为采用高斯加权的中值直方图均衡，从中可以看出部分条纹未能有效地去除，且算法过度平滑，影响了目标等主要观测物的成像质量。图5是本文算法的效果图，可以看出本算法取得了较好的校正效果。图6为目标点及其3×3领域的灰度值。

图3 原始图像

图4 中值直方图均衡采用高斯加权

图5 中值直方图均衡采用IQR加权

从图6中可以看出，本文提出的算法可更好的保留目标信息。

最后，根据公式(8)计算的各种情况的非均匀性，如表1所示：

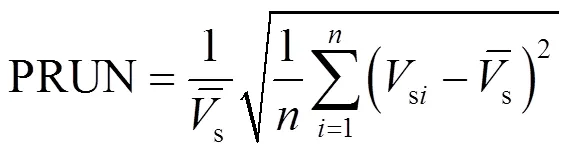
高斯加式中：为探测器各个单元响应信号的平均值。

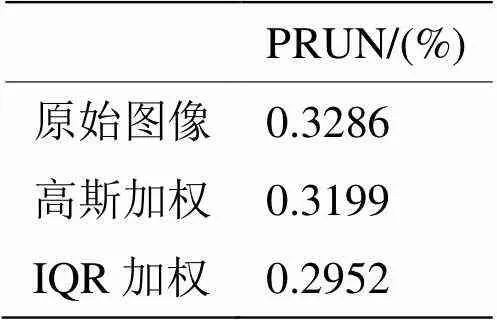
表1 非均匀性（PRUN）

3 结论

本文采用Tendero所提出的基于中值直方图均衡的校正算法对红外线列扫描系统进行非均匀性校正。并且在计算中值直方图时，对加权算子进行了改进。实验表明，本算法简单快捷，易于工程实现，不仅可避免一般场景法存在的“鬼影”问题，而且具有较好的图像视觉质量。并且校正后的剩余非均匀性也比采用高斯加权的剩余非均匀性低。

[1] Milton A F, Barone F R, Kruer M R. Influence of nonuniformity on infrared focal plane array performance[J]., 1985, 24(5): 855-862．

[2] Friedenberg A, Goldbatt I. Non-uniformity two-point linearcorrection errors in infrared focal plane arrays[J]., 1998, 37(4): 1251-1253．

[3] Torres S N, Hayat M M. Kalman filtering for adaptive non-uniformity correction in infrared focal plane arrays[J]., 2003, 20(3): 470-480.

[4] S. Cain, E. Armstrong, B. Yasuda. Joint estimation ofimage, shifts, and non-uniformities from infrared images[C]//(.) 1997, 1: 121-132.

[5] D Scribner, K Sarkady, M Kruer. Adaptive retina-likepreprocessing for imaging detector arrays[C]//, 1993, 3: 1955-1960．

[6] J G Harris, Y M Chiang. Nonuniformity correction usingconstant statistics constraint: analog and digital implementation[C]//, 1997, 3061: 895-905．

[7] D Scribner, K Sarkady, M Kruer, et al. Adaptive non-uniformity correction for IR focal plane arrays using neuralnetworks[C]//, 1991, 1541: 100-109．

[8] Harris J G, Chiang Y. Minimizing the ghosting artifact in scene-based nonuniformity correction[C]//, 1998, 3377: 106-113．

[9] Rossi A, Diani M, Corsini G. Temporal statistics de-ghosting for adaptive non-uniformity correction in infrared fo-al plane arrays[J].., 2010, 46(5):348-349．

[10] Vera E, Torres S. Ghosting reduction in adaptive non-uniformity correction of infrared focal-plane array image sequences[C]//, 2003, 3: II-1001-4．

[11] Russell C, Hardie, Frank Baxley, et al. Scene-based non-uniformitycorrection with reduced ghosting using a gated LMS algorithm[J]., 2009, 17(17): 14918-14933.

[12] Tendero, Y., Gilles, J., Landeau, S., et al. Efficient single image non-uniformity correction algorithm[C]//(), 2010, 7834: 10.

[13] Delon, J.. Midway image equalization[J]., 2004, 21(2): 119-134.

[14] Delon, J.. Movie and video scale-time equalization application to flicker reduction[J]., 200615: 241-248.

[15] Kaushal D. Buch.. Decision based non-linear filtering using interquartile range estimator for Gaussian signals[C]//, 2014: 1-5.

[16] I. Scollar, B. Weidner, T. S. Huang. Image enhancement using themedian and the interquartile distance[J]., 1984, 25(2): 236-251.

[17] F. A. Jassim. Image denoising using interquartile range filter with local averaging[J].: 2013, 1302: 1007.

NUC of IR Scanning System Based on Midway Histogram Equalization

ZHOU Ni，ZHANG Chenghong，LI Fanming

(,,200083,)

A new way to correct non-uniformity (NU) in scanning infrared-type images is proposed，which is kind of scene-based NUC proposed by Tendero, namely, midway histogram equitation. And IQR is used instead of gauss kernel while calculating its midway histogram. The strength of this approach lies in its simplicity and low computational cost. It needs no test-pattern or calibration and produces no “ghost-artifact”. Experimental results indicate that this method can be well used in IR scanning system.

IR scanning system，midway histogram equalization，scene-based NUC，IQR filter

TN219

A

1001-8891(2017)01-0058-04

2016-08-29；

2016-12-22.

周妮（1981-），女，硕士，副研究员，主要从事红外成像，告警，跟踪等方面的科研工作。