航天器编队的六自由度循环追踪协同控制
罗建军,周 亮,蒋祺祺,张 博
(1.西北工业大学航天学院,西安710072;2.航天飞行动力学技术重点实验室,西安710072; 3.深圳大学机电与控制工程学院,深圳518060)
航天器编队的六自由度循环追踪协同控制
罗建军1,2,周 亮1,2,蒋祺祺1,2,张 博2,3
(1.西北工业大学航天学院,西安710072;2.航天飞行动力学技术重点实验室,西安710072; 3.深圳大学机电与控制工程学院,深圳518060)
针对航天器编队的姿轨协同控制问题,提出一种使用循环追踪策略的六自由度(6-DOF)协同控制方法。首先,结合Lagrangian形式的姿态动力学和轨道动力学方程,建立航天器编队的六自由度相对运动模型;然后,以线性双积分系统的循环追踪算法为基础,分别设计可跟踪动态目标的循环追踪算法和航天器匹配自然周期相对运动的循环追踪算法。综合上述两种算法,设计航天器编队六自由度协同控制的循环追踪算法。该算法可实现航天器编队空间圆构型初始化,跟踪动态的期望姿态和相对运动。仿真结果证明了所提出的航天器编队六自由度协同控制的循环追踪算法的有效性。
航天器编队;循环追踪;六自由度;姿轨协同控制;Lagrangian方程
0 引 言
与传统的单平台航天器相比,分布式航天器系统具有结构灵活、可靠性高、生命周期长以及发射风险低等优点,不仅可以实现传统航天器无法实现的任务,如合成孔径、长基线任务,还具有传统航天器所不具备的快速空间响应能力和空间攻防对抗下的任务保护能力[1-3]。分布式自主协同控制(或称多智能体协同控制)是航天器编队自主协同飞行的重要研究方向和技术核心。实际任务往往要求对多个航天器的相对位置和相对姿态进行协同控制[4-7]。
近年来很多学者开展了航天器六自由度(6 degree of freedom,6-DOF)协同控制的研究,并取得一定进展。航天器六自由度的协同控制,目前主要采用的方法是将航天器相对姿态和轨道描述为Lagrangian方程形式的六自由度模型,借助Lagrangian方程的反对称性等性质设计协同控制律[4]。吕跃勇等[5]和Lv等[6]在考虑输入受限和参数不确定情况下,基于退步控制设计了协同控制律,并通过加入指令滤波器,使控制信号满足输入约束。在此基础上针对输入受限和模型参数不确定,又设计了一种满足输入有界条件的自适应L2增益干扰抑制控制器。张博[7]在多Lagrangian系统线性和非一致控制律基础上,分别设计了航天器协同飞行交会对接任务和编队构型控制任务的两个6-DOF协同控制算法,并研究了姿轨控制推力器配置与控制分配算法。毕鹏等[8]采用一致性理论,设计了一种非线性控制律。Chung等[9]将卫星编队相对轨道和姿态运动描述为Lagrangian系统,设计了一种分布式非线性协同控制律以实现卫星编队的六自由度协同控制。Kristiansen等[10]针对模型参数不确定,分别设计了基于无源方法的PD+控制器、滑模控制器及后退控制器3个控制器。Ren[11]在有向拓扑结构下研究了多星系统的相对轨道和相对姿态,但是将航天器相对运动建模为简单的线性二阶积分系统。
循环追踪策略是一种分布式协同控制策略,采用单向信息拓扑,实现n个智能体前后跟踪,首尾相接。该方法在一致性问题基础上,通过加入一个旋转耦合矩阵使每个自主体的控制输入通过旋转角产生偏置,最终使所有自主体形成期望几何构型[7]。循环追踪策略的基本原理是通过选择不同的旋转角,使闭环系统特征值配置在复平面的左半平面、虚轴或右半平面,实现以下3种基本的运动模式:共点模式、圆形编队模式、对数螺旋线模式。Ren[12]针对一阶系统和二阶系统,设计了循环追踪算法,并通过分析闭环系统状态转移矩阵的特征值来分析系统稳定性,并研究信息拓扑、阻尼增益及耦合矩阵对集群运动的影响。Mier-Y-Teran-Romero等[13]考虑了时间延迟、噪声的存在,采用循环追踪方法研究了非线性自主体的编队控制。Riberos等[14]对循环追踪理论进行了研究,探讨了其在深空探测干涉仪成像、卫星编队飞行等空间任务的应用。但是,现有文献中循环追踪策略主要应用于航天器编队轨道控制中,目前还没有将其应用于航天器编队飞行六自由度协同控制的文献。
本文基于线性双积分系统的循环追踪算法[14-15],设计了可跟踪动态目标的协同控制循环追踪算法,并结合航天器近地环境自然周期相对运动特性,设计了与自然构型匹配的循环追踪算法。在此基础上,设计了一种编队飞行六自由度循环追踪算法,同时跟踪航天器编队的期望姿态和相对运动轨迹,实现了航天器六自由度姿轨协同控制。
1 航天器编队的六自由度相对运动模型
1.1 单个航天器的六自由度相对运动模型[7]
采用修正的罗德里格斯参数 (Modified Rodriguez parameters,MRPs)描述航天器体坐标系相对于惯性坐标系的方位,可以避免求解复杂的约束方程,并且没有冗余参数,同时能够减少奇异性影响,其具体表示为
式中:e为欧拉轴,θ为绕e轴的旋转角。
采用MRPs表示的姿态运动学方程为
航天器的姿态动力学模型为
式中:J为对称正定的航天器转动惯量阵,τ=[τ1,τ2,τ3]T,是作用于航天器上的控制力矩或干扰力矩,ω =[ω1,ω2,ω3]T,为航天器相对于惯性系的姿态角速度,[·]×表示叉乘矩阵。
联立式(1)和式(2)可得采用MRPs描述的某个编队航天器Si,i=1,…,N的姿态运动方程为
定义参考轨道坐标系Oxyz,原点位于编队参考中心,x轴沿矢径方向,z轴沿垂直轨道面的角动量方向,y轴由右手法则决定且Oxyz组成右手直角坐标系。假设编队中所有航天器同构(质量统一为m),可得Lagrangian形式的相对轨道动力学方程:
若参考航天器S0运行在不受摄动影响的圆参考轨道上,轨道半径为r0,轨道角速度为n,编队航天器Si,i=1,…,N的相对运动动力学方程可采用如下的C-W方程描述
定义某个编队航天器Si,i=1,…,N的六自由度运动状态为,结合式(3)~(4),可得
式中:
1.2 航天器编队的六自由度相对运动模型
2 轨迹协同控制的循环追踪算法
2.1 线性双积分系统的循环追踪算法[14]
设i∈{1,…,N}表示三维空间多智能体系统中第i个智能体,Xi(t)=[xi(t),yi(t),zi(t)]T∈R3,表示i在t≥0时刻的位置状态,运动模型为线性双积分系统:
考虑如下线性双积分系统的循环追踪算法
式中:km∈R+,kn∈R,当i=N时,XN+1与等效表示为X1与。Q(α)是旋转角为α的三维旋转矩阵,其旋转轴为[0,0,1]T,则有
由式(9)可知,循环追踪控制需要每个智能体相对于参考点的位置(kn≠0)和速度信息(kn≠-km)。
在循环追踪算法(9)的作用下,N个智能体组成的多智能体系统可写为
选择适当的参数,在式(9)的作用下,多智能体系统在三维空间可形成3种典型的运动模式:聚集运动、圆构型周期运动和对数螺旋线运动。关于参数和多智能体的运动特征有如下3个定理。
定理1.对闭环系统(10),若 -km不是(α)的特征值,则系统状态矩阵(α)的特征值由以下两部分组成:
2)3 N个重根 -km。
定理2.对闭环系统(10),假设kn>0,若0≤<π/N,则(α)的所有特征值都位于左半复平面内(即(α)的所有特征值都位于左半复平面内),收敛到原点上;若π/N≤<2π/N,则有如下结论:
1)若kn>2sin(π/N)sin(α-π/N),所有特征值位于左半开复平面内;
2)若kn=2sin(π/N)sin(α-π/N),有两个非零特征值位于复平面虚轴上,其余特征值位于左半开平面内;
3)若kn<2sin(π/N)sin(α-π/N),两个非零特征值位于右半开平面内,其余非零特征值位于左半开平面内。
定理3.对多智能体系统(10),若 -km不是(α)的特征值,且kn>0,则系统从非零初始状态开始,在式(9)作用下指数收敛:
当kn>2sin(π/N)sin(α-π/N),收敛到原点;
当kn=2sin(π/N)sin(α-π/N),收敛为一个以原点为圆心的圆构型上;
当kn<2sin(π/N)sin(α-π/N),收敛到一个均匀分布的对数螺旋线编队。
2.2 追踪动态目标的循环追踪算法
在线性双积分系统循环追踪算法(9)的基础上,加入跟踪的动态目标状态,可设计如下的可追踪动态目标的循环追踪算法[7,14]:
由式(12)与式(10)的对比可见,可追踪动态目标的线性双积分系统循环追踪算法(11)是式(9)的推广,因此定理1、定理2、定理3也都适用于式(11)。
2.3 追踪轨迹匹配自然构型的循环追踪算法
对于航天器的协同飞行,减少航天器编队飞行过程中的燃料消耗,应该充分利用航天器间的自然周期相对运动。为了实现航天器自然周期相对运动,减少燃料消耗,本文采用同胚映射将编队航天器的追踪轨迹转换到航天器间的自然周期相对运动构型,实现考虑自然周期相对运动几何形态的相对运动协同控制[7,14]。
采用同胚映射的方法可以将循环追踪的轨迹转换到特定的几何形状。相似变换是一种常用的同胚映射方法。通过选择合适的线性可逆变换 T∈ RN×N对循环追踪算法的旋转矩阵Q(α)进行相似变换,可以使原来收敛的系统收敛到新的不变集[7,14]。这样,状态就会产生如下转换
因此,循环追踪算法产生的圆构型在同胚映射作用下就能够与航天器相对运动的椭圆形自然构型相匹配,从而形成自然的周期相对运动。
假设参考航天器S0在近圆轨道运行,即e0≈0,且不考虑J2项摄动的影响,选取变换矩阵如下:
式中:z0和φz是两个可调参数,决定了圆参考轨道周期构型的法向振幅和相位角。
对线性双积分系统的循环追踪算法(9)的旋转矩阵进行相似变换,可设计如下的匹配自然构型的航天器编队循环追踪算法:
式中:kc=n/[2sin(π/N)cos(α-π/N)]。其余参数的含义与式(9)相同。下面对控制性能进行分析。
式(15)除去第一项的剩余部分如下:
N个航天器组成的编队系统可写为
由定理1,若 -km不是(α)的特征值,则式(16)中状态矩阵A~(α)的特征值由以下两部分组成:
由式(17)可得,当kn>0,π/N≤<2π/N时,特别地,当kn=2sin(π/N)sin(α-π/N),有两个位于虚轴的特征值λ1,2=±j2kcsin(π/N)cos(απ/N),其余特征值均位于左半平面。虚轴上的特征值决定了圆编队的角速度,即圆编队角速度ωN= 2kcsin(π/N)cos(α-π/N)。
要实现匹配自然周期相对运动构型,除了几何形状、尺寸外,还要匹配运动角速度(频率),即ωN=n,则kc=n/[2sin(π/N)cos(α-π/N)]。
根据文献[14]中的命题3.4.1,以及定理2和定理3,式(15)能够保证闭环系统稳定。
当t→∞ ,编队系统中的航天器Si,i=1,…,N将收敛到以下构型[14]:
式中:α0,i=2π(i-1)/N,aE为航天器相对运动椭圆形自然构型的长半轴,由所有航天器初始状态决定。将式(14)代入式(18),并对参考轨道坐标系的方向分量进行化简,可得
式(19)为由C-W方程描述的航天器相对运动的椭圆形自然构型。将式(19)代入式(5)易得,当Xi(t)→Xdi(t),i=1,…,N,fi→0。
3 六自由度协同控制的循环追踪算法
圆编队构型在实际中有着广泛的应用,根据定理3的情况2),选择适当的参数,使用可追踪动态目标的循环追踪算法(11)和追踪轨迹匹配自然构型的循环追踪算法(15),结合航天器编队的六自由度相对运动模型,可以在得到匹配自然构型圆编队轨迹的同时实现姿态一致。
将式(20)~(21)代入式(6)可得:
根据定理3,选择合适的参数α、km1、km2、kn1和kn2,就可以实现空间圆编队任务。
4 仿真校验
4.1 仿真参数设置
应用航天器编队六自由度协同控制的循环追踪算法(20),实现5个在近地轨道飞行的航天器的姿态同步、编队构型初始化以及编队构型的保持控制。
初始条件如下:设5个航天器同构,质量均为50 kg,转动惯量均为
航天器编队系统内的信息拓扑图G为单向循环追踪环,如图1所示。序号1~5表示航天器S1~S5,仿真结果如图2~5所示。
5个航天器的初始姿态MRPs与初始角速度如表1所示。
设参考轨道是高度为679.9718 km的圆轨道,轨道倾角75°,5个航天器相对于参考轨道S0的初始位置与初始速度如表2所示。
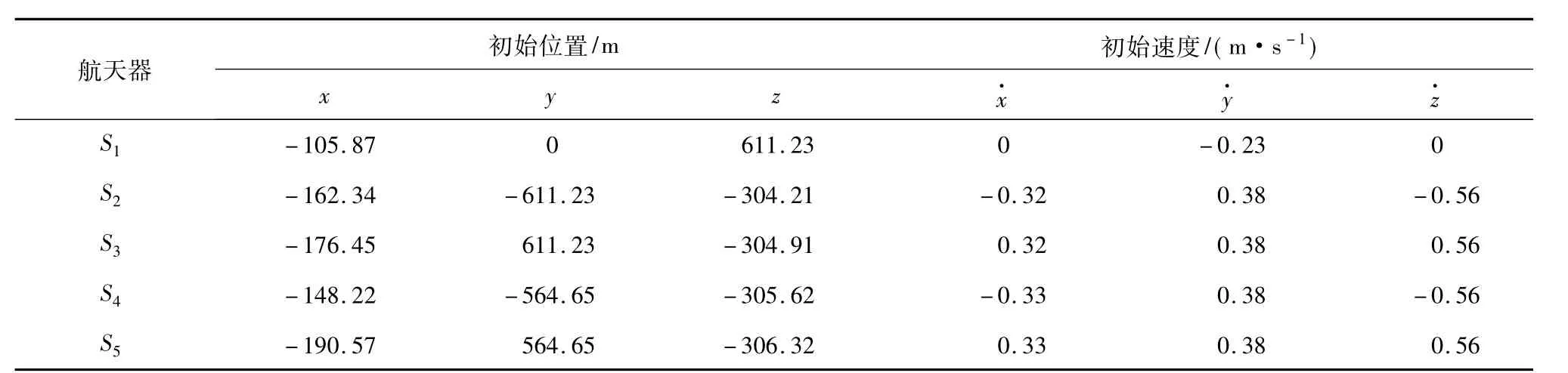
表2 初始位置和初始速度Table 2 Initial position and velocity
追踪角为α=1.5π/N,N=5为航天器数目。给出控制参数:km1=0.01,km2= 0.01,kn1= 2sin(π/N)sin(α-π/N)+0.2,kn2=2sin(π/N)sin(α-π/N)-0.2,0<t≤2T,kn2=2sin(π/N)sin(απ/N),2T <t≤3T,kc=n/(2sin(π/N)cos(απ/N))。其中自然周期频率。在变换矩阵Tc(式(14))中,选择(空间圆构型), φz=0°。
5个航天器协同飞行的期望相对运动为等相位分布在半径为1 km的空间圆构型,并且期望姿态运动为:=0.3547,=0.0564,=0.2870。每个航天器上12个推力器,每个推力器的最大推力为1 N,具体配置方案参考文献[16-17]。
4.2 仿真结果分析
从初始条件开始,在式(20)的作用下,实现5个航天器姿态的同步、编队构型的初始化与编队保持,仿真时间为3个轨道周期3T(17700 s)。
图2是5个航天器协同飞行的构型建立过程,5个实心圆分别表示航天器的初始位置,5个五角星分别表示航天器的最终位置,可见5个航天器由初始状态在式(20)的控制作用下可以等相位分布在空间圆构型上。
图3是5个航天器的姿态MRPs、角速度的同步过程及控制力矩变化曲线,曲线最终收敛到期望姿态。由图3可知,在式(20)的作用下,约在500 s时,5个航天器姿态MRPs同步到期望姿态,角速度趋向0,控制力矩也趋向0,说明姿态同步已完成,因此仅绘制出前600 s的仿真曲线。
图4为整个任务周期内5个航天器在式(20)的控制作用下的相对位置、速度及控制力变化曲线。任务周期分为两个阶段:第一阶段,在0<t≤2T时间段内,利用循环追踪螺旋线运动模式,执行编队的初始化任务;第二阶段,在2T<t≤3T时间段内,利用循环追踪圆构型运动模式,使编队保持空间圆相对运动。从控制力变化曲线来看,2T时刻(11800 s)是操作任务的切换点,控制力存在跳变,这是由于算法由螺旋线模式转换到圆构型模式导致的。控制力维持在10-3量级,符合燃料消耗需求。
由图5可见,在式(20)的作用下,5个航天器之间的相对距离和相对速度呈周期变化,达到了稳定的六自由度编队协同运动状态。
5 结 论
本文首先以Lagrangian形式的姿态动力学和轨道动力学为基础,建立了航天器六自由度相对运动动力学方程。然后,基于线性双积分系统的循环追踪算法,设计了可跟踪动态目标的循环追踪算法。然后结合航天器自然周期相对运动特性,使用同胚映射方法,设计了匹配自然构型的循环追踪算法。综合上述两种循环追踪算法,进一步设计了航天器编队飞行六自由度协同控制的循环追踪算法。仿真结果表明,所设计的使用循环追踪的六自由度协同控制算法,可以使多个航天器同时准确跟踪期望姿态运动和相对轨迹运动,可实现航天器圆编队构型建立、航天器姿轨协同和编队构型的保持控制。
[1] 杨震,孟新,牛文龙,等.多航天器协同探测星簇构型探测效能的评价方法[J].宇航学报,2015,36(9):981-987.[Yang Zhen,Meng Xin,Niu Wen-long,et al.A evaluation method for multi-spacecraft formation detection efficiency[J].Journal of Astronautics,2015,36(9):981-987.]
[2] 谭天乐.椭圆轨道交会、悬停与绕飞的全状态反馈控制[J].宇航学报,2016,37(7):811-818.[Tan Tian-le.Full state feedback control of rendezvous,hovering and fly-around in elliptical orbit[J].Journal of Astronautics,2016,37(7):811-818.]
[3] 张永合,梁旭文,周远强,等.无阻力双星编队的满系数矩阵MIMO定量反馈控制[J].宇航学报,2016,37(7):819-828.[Zhang Yong-he,Liang Xu-wen,Zhou Yuan-qiang,et al.Full-matrix MIMO QFT controller design for drag free satellites in dual formation[J].Journal of Astronautics,2016,37(7):819-828.]
[4] Accardo D,Aguttes J P,Al-berti G.Distributed space missions for Earth system monitoring[M].New York:Springer Science&Business Media,2012.
[5] 吕跃勇,胡庆雷,马广富,等.带有控制受限的卫星编队飞行六自由度自适应协同控制[J].控制理论与应用,2011,28(3):321-328.[Lv Yue-yong,Hu Qing-lei,Ma Guang-fu, et al.Adaptive synchronized control with 6 degrees of freedom and bounded input for satellite formation flight[J].Control Theory&Applications,2011,28(3):321-328.]
[6] Lv Y Y,Hu Q L,Ma G F,et al.6 DOF synchronized control for spacecraft formation flying with input constraint and parameter uncertainties[J].ISA Transactions,2011,50(4):573-580.
[7] 张博.多航天器协同飞行分布式控制研究[D].西安:西北工业大学,2013.[Zhang Bo.Research on distributed control for multiple spacecraftcooperative flying[D].Xi’an: Northwestern Polytechnical University,2013.]
[8] 毕鹏,罗建军,张博.一种基于一致性理论的航天器编队飞行协同控制方法[J].宇航学报,2010,31(1):70-74.[Bi Peng,Luo Jian-jun,Zhang Bo.A synchronized control method for spacecraft formation flying based on consensus theory[J].Journal of Astronautics,2010,31(1):70-74.]
[9] Chung S J, Ahsun U, Slotine J J E. Application of synchronization to formation flying spacecraft: Lagrangian approach[J].Journal of Guidance,Control,and Dynamics,2009,32(2):512-526.
[10] Kristiansen R,Nicklasson P J,Gravdahl J T.Spacecraft coordination controlin 6DOF: Integrator backstepping vs passivity-based control[J].Automatica,2008,44(11):2896-2901.
[11] Ren W.Formation keeping and attitude alignment for multiple spacecraft through local interactions[J].Journal of Guidance,Control,and Dynamics,2007,30(2):633-638.
[12] Ren W.Collective motion from consensuswith Cartesian coordinate coupling[J].Automatic Control,IEEE Transactions on,2009,54(6):1330-1335.
[13] Mier-Y-Teran-Romero L,Forgoston E,Schwartz I B.Coherent pattern prediction in swarms of delay-coupled agents[J].Robotics,IEEE Transactions on,2012,28(5):1034-1044.
[14] Riberos R,Luis J.New decentralized algorithms for spacecraft formation control based on a cyclic approach[R].Cambridge,America:Massachusetts Institude of Technology,2010.
[15] Yang H X,Yang T,Zhang W H.Review on cyclic pursuit in spacecraft formation flying[A].International Conference on Recent Advances in Space Technologies,IEEE,2011:576-580.
[16] Curti F,Romano M,Bevilacqua R.Lyapunov-based thrusters' selection for spacecraft control:analysis and experimentation[J].Journal of Guidance,Control,and Dynamics,2010,33(4): 1143-1160.
[17] 唐生勇,张世杰,陈闽.交会对接航天器推力分配算法研究[J].宇航学报,2008,29(4):1120-1125.[Tang Shengyong,Zhang Shi-jie,Chen Min.Research on a thrust allocation algorithm of spacecraft in RVD[J].Journal of Astronautics,2008,29(4):1120-1125.]
通信地址:西安市西北工业大学251信箱(710072)
电话:(029)88493685,(029)88493350
E-mail:jjluo@nwpu.edu.cn
(编辑:牛苗苗)
6 DOF Coordinated Control Using Cyclic Pursuit for Spacecraft Formation
LUO Jian-jun1,2,ZHOU Liang1,2,JIANG Qi-qi1,2,ZHANG Bo2,3
(1.School of Astronautics,Northwestern Polytechnical University,Xi’an 710072,China; 2.National Key Laboratory of Aerospace Flight Dynamics,Xi’an 710072,China; 3.College of Mechatronics and Control Engineering,Shenzhen University,Shenzhen 518060,China)
A 6 degree of freedom(6-DOF)attitude and orbit coordinated control method using cyclic pursuit is proposed for spacecraft formation flying.Firstly,a decentralized coordinated tracking cyclic pursuit algorithm is developed based on the linear second-order cyclic pursuit control algorithm.Then,a cyclic pursuit algorithm which can match the natural period configuration of satellites is improved based on a similarity transformation to the rotation matrix.Next,a proposed 6-DOF coordinated control method which uses cyclic pursuit algorithm is applied to both orbital and attitude dynamics formulated as the integrated Lagrangian equations.The three dimentional circular formation composed of multiple spacecraft can be realized by the proposed algorithm and the attitude of an arbitrary number of spacecraft can be synchronized to the constant reference states simultaneously.Numerical simulation results demonstrate the efficiency of the proposed algorithm.
Spacecraft formation flying;Cyclic pursuit;6 degree of freedom(6-DOF);Attitude and orbit coordinated control;Lagrangian equations
V448.2
A
1000-1328(2017)02-0166-10
10.3873/j.issn.1000-1328.2017.02.008
罗建军(1965-),男,博士,教授,主要从事航天飞行动力学、导航、制导与控制等方面的研究。
2016-08-16;
2016-11-21
国家自然科学基金(11072194,61690211)

