带有振动抑制的压电结构动态形状主动控制

王晓明，周文雅，寻广彬，吴志刚，

(1.大连理工大学工程力学系工业装备结构分析国家重点实验室，大连116024; 2.大连理工大学航空航天学院，大连116024)

带有振动抑制的压电结构动态形状主动控制

王晓明1，周文雅2，寻广彬1，吴志刚1，2

(1.大连理工大学工程力学系工业装备结构分析国家重点实验室，大连116024; 2.大连理工大学航空航天学院，大连116024)

针对压电结构在动态形状主动控制过程中的振动抑制问题，以压电纤维复合材料作动器驱动的悬臂板为研究对象，建立了结构有限元模型，并给出了控制方程。由于不合理的作动器电压加载方式会导致结构的瞬态和残余振动，影响形状控制精度和系统稳定性;本文在静态形状控制基础上，提出电压加载时间历程的优化问题。结合有限差分法和二次规划算法对优化问题进行求解。最后，以悬臂板弯曲形状控制为例，对所提动态形状控制算法进行了校验;并与阶跃、斜坡等电压加载方式进行了对比。结果表明，利用优化后的电压加载时间历程，能够有效抑制结构的瞬态和残余振动，提高动态形状控制效果。

压电作动器;板结构;形状控制;振动抑制;二次规划

0 引 言

随着航空航天领域的发展，柔性结构越来越多的应用于飞行器结构设计中，如太阳能帆板、柔性机翼、大型天线反射面等。利用智能材料实现柔性结构的形状主动控制能够有效提高结构精度、增强系统性能并提高结构适应能力［1－2］。例如:主动控制翼面形状能够有效改善机翼气动特性、提高飞行性能［3］;主动控制反射器的型面形状能够有效修正型面误差，提高反射精度［4］。

随着智能材料的发展，压电功能复合材料因其能源转换快速、作用频带宽、精确度高等诸多优点，在结构型状控制领域得到了广泛的研究和应用［5］。结构的形状控制分为静态与动态形状控制［6］，其中静态形状控制是将结构的变形过程作为静态或准静态过程进行分析，而不考虑变形的动态过程。目前的研究多集中于结构静态形状控制［7－9］。结构的动态形状控制则需考虑系统各变量随时间的变化过程，如驱动电压加载时间历程的影响。简单的电压加载方式(如阶跃、斜坡等信号)往往会引起结构的瞬态和残余振动，严重影响控制精度和系统稳定性［10］。因此，为满足结构的形状精度和稳定性等任务要求，需要有效抑制结构变形过程中的振动［11］;以实现连续、光滑的高精度动态形状控制效果［12］。与传统的结构振动抑制不同的是，结构在变形过程中没有一个固定的基准状态;此时的振动抑制需要计及形状控制中的时变效应［13］。由于压电结构的动态响应与电压加载方式有直接关系，因此可以通过优化、规划驱动电压的加载时间历程，达到抑制结构变形过程中的振动的目的，以提高动态形状控制精度。国内在压电结构的动态形状控制方面研究还相对较少。有国外研究人员以结构振动最小［10］、控制能量消耗最小［14］为目标函数研究了压电结构的动态形状控制。本文的目标函数将同时考虑结构振动抑制效果和控制能量消耗，并计及作动器电压达到稳态值后结构的残余振动，以综合提高结构动态形状控制效果。

本文以压电纤维复合材料驱动的悬臂板结构为研究对象，建立其动力学方程和控制方程。针对阶跃、斜坡等简单的电压加载方式易引起结构瞬态和残余振动的问题，本研究在静态形状控制基础上，提出了电压加载时间历程的优化问题，并给出了二次规划求解方法。最后以板结构的弯曲形状控制为例，验证了控制算法的有效性。

1 压电结构动力学模型

压电驱动的悬臂板结构示意图如图1所示。研究中采用的压电作动器为宏纤维复合材料(Macro fiber composites，MFC)，纤维铺设方向为板结构的长度方向。施加电压后，在压电作动器驱动下，板结构会产生如图所示的弯曲变形。

1.1 结构有限元模型

采用四节点板单元建立结构的有限元模型，如图2(a)所示。模型包含两种基本单元:被动单元和主动单元(铺设有压电材料的单元);两种单元横截面如图2(b)和2(c)所示。由于铺设的压电纤维复合材料会引起主动单元刚度和质量特性的改变，研究中利用复合材料层合板理论计算主动单元的刚度阵和质量阵［15］。

利用哈密顿原理可以导出单元的动力学方程［16］。其中被动单元的动力学方程可表示为

主动单元的动力方程可表示为

式中:uN为单元节点位移，Muu和Kuu为基板材料层的单元质量和刚度矩阵，和表示压电材料层引起的单元质量和刚度增量。Fp为压电驱动载荷，并可用下式计算［17］

其中

式中:B1和B2分别为应变－位移矩阵和电场－电势矩阵，V为电压值，e为压电应力系数矩阵。

通过组装被动单元和主动单元，可得到总体刚度阵和质量阵。为模拟真实的结构动力学响应，还需考虑阻尼效应。因此，压电驱动悬臂板的整体有限元方程可以表示为

式中:x为节点位移向量，M、K分别表示结构整体质量、刚度矩阵，C为阻尼矩阵，研究中采用瑞利阻尼假设，Bu为作动器位置矩阵，u为加载电压向量，其维数与作动器个数一致。

1.2 状态空间模型

由于有限元模型单元数、节点数较多，动力学方程阶数较大，不便于进行控制律设计。研究中采用模态分解法进行模型降阶［18］，引入模态坐标变换

式中:q为广义坐标向量，Φ为振型矩阵。将上述方程代入方程(5)，并在式子两端左乘ΦT;进一步整理可得

为便于设计控制器，可将系统模型表示为状态空间形式如下

其中

系统的输出可根据不同任务或者控制目标而设定。本文研究板结构的弯曲形状控制，因此将端部挠度作为控制输出变量;即

式中:y表示压电驱动的悬臂板结构的端部挠度，Cy为输出矩阵。

2 静态与动态形状控制

压电结构的形状控制可以分为静态与动态形状控制［6］。静态形状控制仅利用静力方程，不考虑系统各变量随时间的变化，用于计算达到理想形状所需的终端加载电压，或在给定电压下结构的稳态变形。动态形状控制则需要计及时间效应，考虑各变量随时间的变化，即不仅需要结构能够精确地达到目标形状，还要求变形过程能够满足一定的动态性能。

以悬臂板结构的弯曲形状控制为例。设板在初始时刻处于未变形状态，且没有电压加载，即X0= 0，u0=0。现在希望通过作动器的驱动，使得其端部挠度y达到期望值yc。首先令状态变量对时间的导数为零，则可以利用下式计算所需的作动器终端稳态电压

确定了压电作动器的初始电压u0和终端电压uf，但电压值从u0到uf的加载时间历程没有确定。从系统模型可知，作动器电压加载时间历程将会对结构的动力学响应产生直接影响。一些简单的电压加载方式(如阶跃、斜坡等)将会激发结构振动模态，产生瞬态和残余振动问题，严重影响控制精度和系统稳定性［10］;相关仿真校验将在第4章给出。

因此，为实现连续、光滑的高精度动态形状控制效果，需要对作动器电压加载时间历程进行优化设计，以抑制结构在变形过程中的振动。

3 优化问题与求解

在带有振动抑制的压电结构动态形状控制中，需要计及时间因素，考虑系统各变量随时间的变化过程。设初始时刻为t0，期望达到目标形状的时间为t1。本研究的目的是设计［t0，t1］时间段内作动器电压的加载时间历程，抑制结构在变形过程中的振动;即设计最优控制输入u(t)，使得结构的振动能量最小。

3.1 优化问题的提法

压电作动器电压加载时间历程的优化问题可描述如下:

寻求最优控制输入

使得性能指标J(见式(13))取得极小值。

式中:P1、P2为半正定加权矩阵，P3为正定加权矩阵，t2表示电压达到终端值uf后的某个时刻。性能指标J中的第一项表征在电压加载过程中结构的瞬态振动能量，第二项表征电压达到终端值uf后结构的残余振动能量，第三项则表示控制能量消耗。通过调节上述权系数矩阵，可对结构振动抑制效果和控制消耗之间进行权衡。

此外，设计变量和性能指标受到系统动力学方程、初边值条件以及压电作动器电压限幅等条件的约束。因此，优化中的约束条件可表示为

式中:umin、umax为压电作动器允许可用的最小、最大加载电压。

基于上述描述，带有振动抑制的压电结构动态形状控制问题已经转化为一个性能指标为二次型表达式的动态优化问题。

3.2 二次规划方法

方程(12)～(14)给出了优化问题的三要素:设计变量、性能指标和约束条件。求解上述优化问题可利用多种优化算法，由于该优化问题的目标函数是系统状态和输入的二次型积分表达式，且约束条件都是线性约束，本研究采用最优化理论中的二次规划方法对优化问题进行求解［19］。

标准的二次规划形式为代数表达式，而上述优化问题的性能指标(13)为积分表达式，系统动力学方程(8)为微分表达式。因此研究中采用有限差分法中改进的欧拉公式对系统动力学方程在时间域上离散，即

式中:Δt为离散时间步长。

通过上述离散处理，第3.1节中提出的电压加载时间历程优化问题可转化为标准的二次规划求解形式。研究中使用二次规划理论中的“有效集”算法［19］对优化问题进行求解。

4 仿真校验

仿真校验中采用的悬臂板和采用的MFC压电作动器的几何、材料参数如表1所示。结构的有限元网格和作动器粘贴位置如图3所示。悬臂板结构共划分30×8个单元，其中每一片作动器覆盖6×6个单元。结构阻尼比设为0.02，用于计算Rayleigh阻尼比例系数。

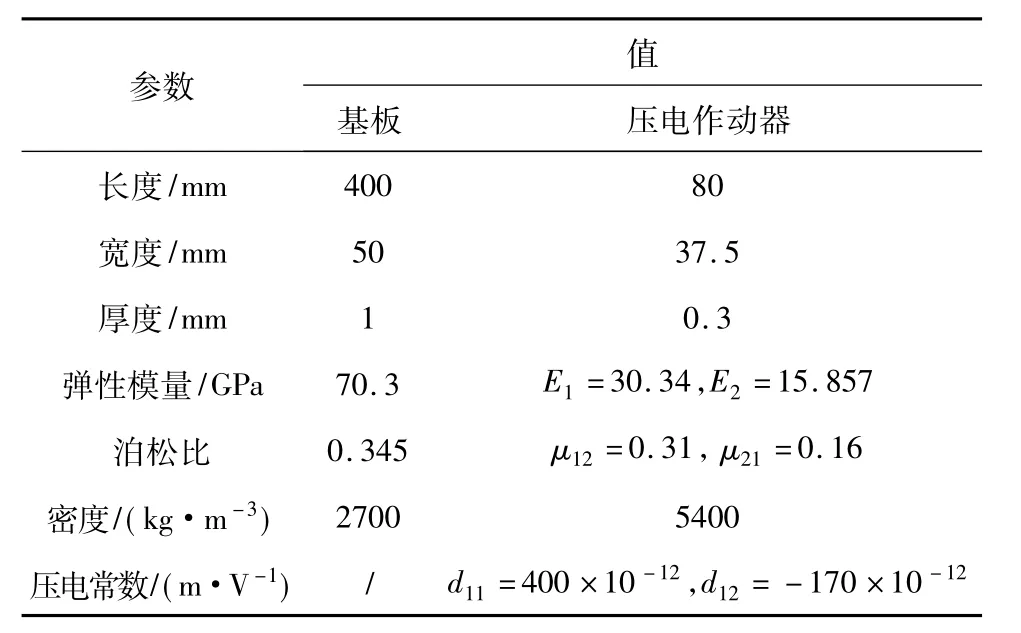
表1 悬臂板和作动器的相关参数Table 1 Parameters of the cantilever plate and piezoelectric actuators

仿真中以悬臂板端部中点(图3中右端的P点)的挠度为控制输出。控制目标是:期望通过压电作动器驱动悬臂板变形，使得端部挠度在t1=1 s时达到稳态值yc=－5 mm。利用式(11)可以求出达到该目标形状所需的2个作动器的终端稳态电压值

图4给出了在作动器终端稳态电压uf的驱动下悬臂板达到的终端稳态形状。

如前所述，作动器电压加载时间历程会对结构的动态响应产生直接影响。在后续仿真中，选取t2=2 s。图5(b)给出了悬臂板端部挠度在阶跃电压加载时间历程ustep(见图5(a))下的动态响应曲线。其中阶跃输入信号的表达式为

图6(b)给出了悬臂板端部挠度在斜坡电压加载时间历程uramp(见图6(a))下的动态响应曲线。其中斜坡输入信号的表达式为

从图5可以看出，在阶跃形式的电压加载历程下，悬臂板结构产生了剧烈振动现象，端部最大挠度超调近1倍，收敛到目标稳态形状需较长时间。由图6可知，在采用了斜坡加载方式后，悬臂板振动在一定程度上得到了抑制，但依然存在明显的瞬态和残余振动。虽然结构的振动幅值在阻尼作用下会逐渐衰减，但所需时间较长。综上可知，简单、不合理的电压加载方式会激发结构振动模态，引起结构的瞬态和残余振动问题，严重影响形状控制精度和系统稳定性。

为了抑制结构在变形过程中产生的振动，采用第3节给出的二次规划方法对作动器电压加载时间历程进行优化设计。优化后的电压加载历程为uoptimal，如图7(a)所示，对应的悬臂板端部挠度响应如图7(b)所示。

首先从图7(b)可以看出，在优化后的电压加载历程作用下，结构变形过程的瞬态和残余振动得到了有效抑制。端部挠度在给定的时间内平滑地从初始值达到目标值;并保持稳定，没有产生超调。从图7(a)可以看出，优化后的作动器电压值在0.5 s前缓慢增加，从而避免激发结构的振动模态，以减小结构在电压加载过程中的瞬态振动幅值。而当电压值接近终端稳态电压时出现了较大幅值的波动。可以理解，正是由于作动器加载电压随时间的合理变化，抑制了结构在变形过程中产生的瞬态和残余振动。

由于作动器加载电压在接近终端值时出现了较大幅值的变化，这虽然有助于结构的快速稳定，但对作动器和控制系统提出了较高的要求。为避免短时间内的电压跳变现象，有两种改善方法:一是对性能指标中第三项进行拆分细化，增加末端控制消耗能量在性能指标中的权重;二是对每一个时间步长Δt内的电压变化进行约束限制，即增加不等式约束。本研究中采用第二种方法，即增加如下约束条件

由图8(a)可以看出，在增加了对电压的不等式约束后，作动器电压值在接近uf时的跳变现象得到了有效改善，更易于在实际中应用。另一方面，悬臂板端部挠度在接近目标稳态值yc时的响应曲线斜率减小了，使得结构的动态变形过程更加平滑，如图8(b)所示。

对比图5～8可以看出，在压电结构的形状主动控制中，不仅需要结构能够精确达到某个形状，还须满足一定的动态性能。利用本文的优化方法，可以规划出更为合理的电压加载时间历程，抑制结构变形过程中的振动，实现连续、光滑的变形效果，提高动态形状控制精度。

5 结 论

本文研究了带有振动抑制的压电结构的动态形状主动控制。推导了压电驱动的悬臂板结构的动力学方程，并采用二次规划方法对作动器的电压加载历程进行了优化设计。利用优化后的电压加载方式能够有效抑制结构在变形过程中产生的振动，提高动态形状控制精度。

［1］ Baier H，Datashvili L.Active and morphing aerospace structures– a synthesis between advanced materials，structures and mechanisms［J］.International Journal of Aeronautical and Space Sciences，2011，12(3):225－240.

［2］ 冷劲松，兰鑫，刘彦菊，等.形状记忆聚合物复合材料及其在空间可展开结构中的应用［J］.宇航学报，2010，31(4): 950－956.［Leng Jin-song，Lan Xin，Liu Yan-ju，et al.Shape memory polymers composites and their applications in deployable structures［J］.Journal of Astronautics，2010，31(4):950－956.］

［3］ 李敏，陈伟民，贾丽杰.压电驱动器的气动弹性应用［J］.航空学报，2009，30(12):2301－2310.［Li Min，Chen Weimin，Jia Li-jie.Application of piezoelectric actuators to aircraft aeroelastic performance enhancement［J］.Acta Aeronautica et Astronautica Sinic，2009，30(12):2301－2310.］

［4］ 王志，曹玉岩，周超，等.柔性压电智能反射面的静态形状控制［J］.光学精密工程，2014，22(10):2715－2724.［Wang Zhi，Cao Yu-yan，Zhou Chao，et al.Static shape control of flexible piezoelectric smart reflectors［J］.Optics and Precision Engineering，2014，22(10):2715－2724.］

［5］ Schrock J，Meurer T，Kugi A.Motion planning for piezoactuated flexible structures:modeling，design，and experiment［J］.Ieee Transactions on Control Systems Technology，2013，21(3):807－819.

［6］ Irschik H.A review on static and dynamic shape control of structures by piezoelectric actuation［J］.Engineering Structures，2002，24(1):5－11.

［7］ 高仁璟，张莹，吴书豪，等.面向结构型状控制的驱动器结构参数与控制电压协同优化设计［J］.光学精密工程，2014，22(6):1538－1546.［Gao Ren-jing，Zhang Ying，Wu Shuhao，et al.Integrated design optimization of actuator structural parameters and control voltages for morphing structural shapes［J］.Optics and Precision Engineering，2014，22(6):1538－1546.］

［8］ 李书阳，郑世杰，王宏涛.PLZT光致伸缩层合梁的非接触形状控制［J］.宇航学报，2012，33(4):514－519.［Li Shuyang，Zheng Shi-jie，Wang Hong-tao.Non-contact shape control of the beam based on PLZT photostrictive actuator［J］.Journal of Astronautics，2012，33(4):514－519.］

［9］ 王剑，赵国忠，刘宝山.压电曲壳单元及其形状控制［J］.工程力学，2008，25(4):224－229.［Wang Jian，Zhao Guozhong，Liu Bao-shan.Shape controlofpiezoelectric shell structures［J］.Engneering Mechanics，2008，25(4):224－229.］

［10］ Kalaycioglu S，Silva D.Minimization of vibration of spacecraft appendages during shape control using smart structures［J］.Journal of Guidance Control and Dynamics，2000，23(3):558－561.

［11］ 徐高楠，黄海，李伟鹏，等.空间挠性结构的stewart平台主动基座振动控制［J］.宇航学报，2015，36(4):438－445.［Xu Gao-nan，Huang Hai，Li Wei-peng，et al.Active vibration control of space flexible structure using stewart platform as active base［J］.Journal of Astronautics，2015，36(4):438－445.］

［12］ 陆宇平，何真.变体飞行器控制系统综述［J］.航空学报，2009，30(10):1906－1911.［Lu Yu-ping，He Zhen.A survey of morphing aircraft control systems［J］.Acta Aeronautica et Astronautica Sinic，2009，30(10):1906－1911.］

［13］ Chakravarthy A，Grant D T，Lind R.Time-varying dynamics of a micro air vehicle with variable-sweep morphing［J］.Journal of Guidance Control and Dynamics，2012，35(3):890－903.

［14］ Hubbard J E.Dynamic shape control of a morphing airfoil using spatially distributed transducers［J］.Journal of Guidance Control and Dynamics，2006，29(3):612－616.

［15］ 沈观林，胡更开.复合材料力学［M］.北京:清华大学出版社，2006:202－204.

［16］ Allik H，Hughes T J R.Finite element method for piezoelectric vibration［J］.International Journal for Numerical Methods in Engineering，1970，2(2):151－157.

［17］ Zhang X，Kang Z.Dynamic topology optimization of piezoelectric structures with active control for reducing transient response［J］.Computer Methods in Applied Mechanics and Engineering，2014，281:200－219.

［18］ 张亚辉，林家浩.结构动力学基础［M］.大连:大连理工大学出版社，2007:85－86.

［19］ 陈宝林.最优化理论与算法［M］.北京:清华大学出版社，2005:417－422.

通信地址:辽宁省大连市高新园区凌工路2号大连理工大学综合实验1号楼(116024)

电话:(0411)84706521

E-mail:xiaomingwang@mail.dlut.edu.cn

周文雅(1981－)，男，博士，副教授，主要从事飞行器动力学与控制方面的研究。本文通信作者。

通信地址:辽宁省大连市高新园区凌工路2号大连理工大学综合实验1号楼(116024)

电话:(0411)84706521

E-mail:zwy@dlut.edu.cn

(编辑:牛苗苗)

Dynamic Shape Control of Piezoelectric Structures with Vibration Suppression

WANG Xiao-ming1，ZHOU Wen-ya2，XUN Guang-bin1，WU Zhi-gang1，2
(1.State Key Laboratory of Structural Analysis for Industrial Equipment，Department of Engineering Mechanics，Dalian University of Technology，Dalian 116024，China; 2.School of Aeronautics and Astronautics，Dalian University of Technology，Dalian 116024，China)

The vibration suppression during the dynamic shape control of the piezoelectric structures is investigated in this paper.The object of this study is a cantilever plate structure with the actuation of the piezoelectric fiber composite materials.The structural finite element model is established and the control equations are given.Some irrational voltage profiles may result in transient and residual vibrations of the structure which would reduce the control precision and stability of the system.A voltage profile optimization problem is formulated based on the static shape control results.The optimization problem is solved using the finite difference method and the quadratic programming.In the end，the bending shape control cases are simulated to verify the effectiveness of the proposed dynamic shape control approach by comparison with the step and ramp voltage profiles.The results show that the transient and residual vibrations of the structure have been effectively suppressed using the optimal voltage profiles and the dynamic shape control performance has been improved.

Piezoelectric actuators;Plate structures;Shape control;Vibration suppression;Quadratic programming

V214.3

A

1000-1328(2017)02-0185-07

10.3873/j.issn.1000-1328.2017.02.010

王晓明(1989－)，男，博士生，主要从事动力学与控制方面的研究。

2016-10-08;

2016-12-08

国家自然科学基金(11432010)