一种基于几何分析的单轴指向磁控算法

寇义民，袁 勤，季艳波，张迎春

(1.深圳东方红海特卫星有限公司，深圳518057;2.哈尔滨工业大学控制科学与工程系，哈尔滨150001)

一种基于几何分析的单轴指向磁控算法

寇义民1，2，袁 勤1，季艳波1，张迎春1，2

(1.深圳东方红海特卫星有限公司，深圳518057;2.哈尔滨工业大学控制科学与工程系，哈尔滨150001)

为满足微小卫星安全模式与其它特定工作模式下的单轴指向需求，提出一种单轴指向磁控方法。该方法包含以下步骤:首先采用空间几何分析方法将指向控制转轴的选择范围扩展到一个平面内，进而在卫星角速度较小的情况下通过惯量阵仿射坐标变换获取当前磁场下可控的角加速度平面，然后在该角加速度平面内以及该平面与转轴平面交线上进行速率阻尼与转向控制，从而实现单轴精准指向。相较于传统方法，本方法的优势包括:无额外的干扰磁场力矩产生，几乎不受轨道形状制约，不要求惯量积为零。在仿真中成功实现卫星单轴对地或对日，进一步校验了该方法的正确性。

微小卫星;单轴指向;主动磁控;空间几何分析

0 引 言

卫星磁控技术具有硬件结构简单、无活动部件、成本低、可靠性高等诸多优点，目前已经在近地轨道飞行器控制中获得了较为广泛的应用。然而与传统控制方法不同的是，磁控力矩方向受地磁场方向的限制，只能在地磁场法平面内产生，这导致系统在任何时刻不是完全可控［1］，故通常难以作为主要姿态控制方法，而仅能用于速率阻尼、动量轮卸载等辅助控制领域。

早期磁控方法是采用经典控制方法设计姿态控制器，求得控制力矩后采用下式反推控制磁矩［2］，如下所示:

式中:T为控制器所需控制力矩，B为地磁场矢量，M即为控制磁矩。由式(1)所获得的磁矩M实际产生的磁控力矩为

式中:Tc为总磁控力矩，其分量T为控制器所需力矩，另一分量Td可以看作是干扰力矩。当B与T接近垂直时Td趋近于0，但实际情况下这几乎是不可能的。由于Td的存在，控制效果必然受到影响，有时甚至会导致系统发散。

为解决此类问题，国内外学者进行了大量研究工作［3－7］。文献［3－4，8］设计了周期线性二次型调节控制器实现三轴稳定控制，文献［5］采用二阶滑膜控器以提升系统鲁棒性，文献［6］设计有界控制器解决磁控系统全局可镇定问题。但前述方法所基于的数学模型均要求卫星轨道必须为太阳同步圆轨道且惯量积趋近于零，否则会产生较大控制偏差，运算也较为复杂。也有学者尝试采用较为简化的控制方案，如文献［7］采用的被动控制方案，虽简单易行，但只能令卫星单轴跟踪地磁场磁力线，应用范围有限。

实际应用中纯磁控大多情况下只是卫星在其它控制部件异常时采取的应急方案，此时通常只需太阳帆板对日来保证能源供应以便为故障排除赢得时间;还有部分任务也只需考虑单轴指向问题，如嫦娥一号卫星奔月期间仅采用了单轴指向控制［9］;此外还可替代重力梯度杆实现天线或载荷对地。为此本文将提出一种单轴指向磁控方法，该方法通过空间几何分析寻找次优转轴平面，以及当前磁力矩所能产生的角加速度平面，在两者的交线上进行角速度控制，从而实现令星体上任一轴向指向惯性空间内任一目标轴的单轴指向控制。相较于现有方法，此方法简单易行，没有额外干扰力矩产生，且基本不受轨道形状和卫星惯量积约束。

1 基础推导与证明

1.1 转轴平面引理证明

引理1的主要作用是扩展了单轴指向控制中转轴的选择范围，除最优转轴外还可以选择同一平面内的其它转轴令指向，为方便起见后续平面DOC简称转轴平面。需注意的是，当与夹角小于90°时所需转角小于180°，反之大于180°。此外，转轴平面的单位法向量P的计算如下所示:

1.2 角加速度平面与转轴平面的交线

根据刚体动力学方程可知，假定飞行器的转动惯量阵为I，瞬时角速度为ω，在控制力矩T作用下飞行器的角加速度为:

因磁力矩T位于地磁场B的法平面内，T一定可以用该法平面内一对非平行的向量X和Y线性表示，即对于任意磁控力矩T必有

其中a和b为常数，将式(13)代入式(12)有

根据仿射坐标变换的平行保持性质，因X与Y不平行，仿射变换后X'与Y'也必定不平行，故磁场法平面内任意力矩T所产生的角加速度都位于向量X'与Y'所张成的平面内(该平面简称为角加速度平面)，由此通过仿射坐标变换形成了由磁场法平面到角加速度平面的一对一映射关系。可按照下式获取角加速度平面的单位法向量Z':

当转轴平面与角加速度平面不平行时必有交线，该交线同时垂直于两平面各自的法线，故可按下式求取两平面交线上的单位向量W

2 控制器设计

当瞬时角速度很小时，磁场法平面内磁控力矩所产生的角加速度近似位于角加速度平面内，那么根据引理1的结论，可按照下述方法实现单轴指向控制:

式中:Kd为控制系数，Z'为角加速度平面单位法向量，ω为星体瞬时角速度，而(ω·Z')Z'为ω中垂直于角加速度平面的分量，故ω－(ω·Z')Z'为ω中平行于角加速度的分量。

进一步在已知角加速度的基础上，利用式(12)来计算磁控力矩:

综上，建立单轴指向控制器的步骤如下:

2)通过式(10)获取转轴平面的单位法向量P;

3)取任一与B不平行的矢量与B叉乘并归一化获得X，X与B叉乘归一化获得Y，由此获取磁场法平面内正交单位向量X和Y;

4)由式(14)和式(15)获得角加速度平面单位法向量Z';

6)由式(16)获得转轴平面与角加速度平面交线上的单位向量W，进而选择合适的控制系数由式(18)～(20)和式(1)计算控制磁矩M。

需要指出的是式(17)与式(18)为PD控制，式(19)为速率阻尼控制，但具体的稳定性数学证明仍有待在后续工作中进一步完善。

3 仿真校验

在Matlab下开展仿真校验，采用东方红海特卫星有限公司研制的KT－1A卫星作为模拟控制对象。该卫星为120 kg的微小卫星，采用偏置动量方式进行姿态控制并安装有三轴磁力矩器。但在仿真过程中动量轮绝对无任何力矩或角速度输出，以确保磁力矩器为唯一控制部件。卫星相关信息参数详见表1，其中轨道为非真实模拟轨道，特地采用了小倾角且存在较小偏心率的近圆轨道以检验控制器性能。分别模拟令星体Z轴指向地心以及令星体－Y轴指向太阳的两种情况开展仿真。

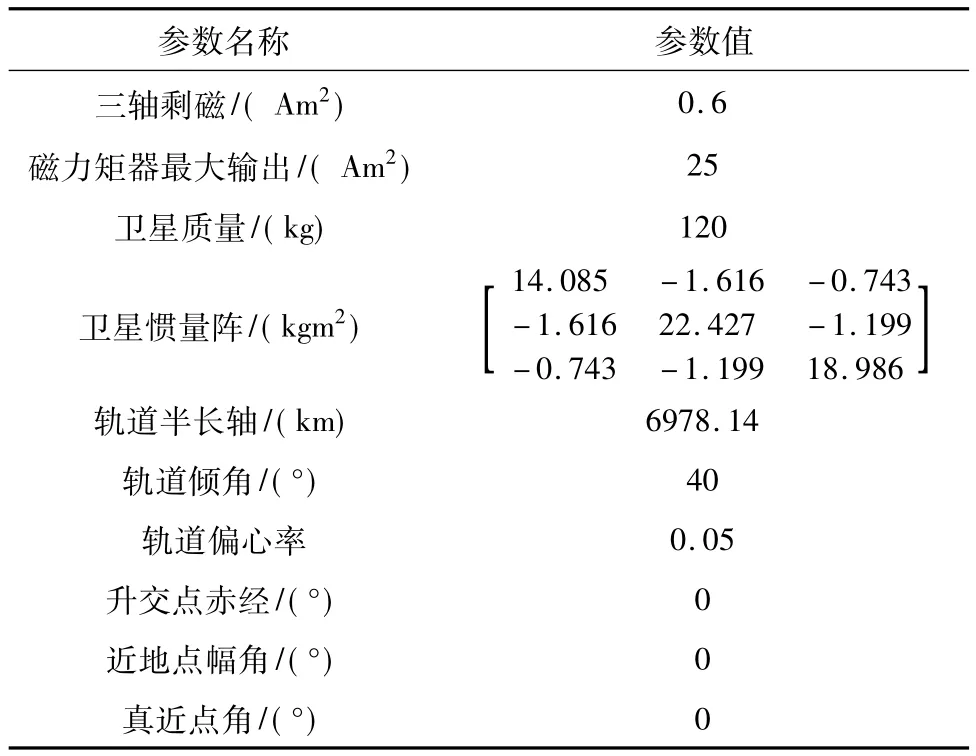
表1 KT－1A卫星参数Table 1 Parameters of KT－1A satellite

星体Z轴对地指向控制的初始仿真参数如表2所示，其仿真结果如图2～5所示。由于轨道高度处于500 km以上，仿真中干扰力矩主要来自重力梯度力矩与剩磁力矩，气阻干扰将被忽略。

由图2中仿真结果可知，系统在约12000 s后达到稳定状态，指向误差可达2°以内。从图3可以看出，卫星相对轨道系偏航角在±180°之间变化，而俯仰角与滚转角很小，故星体非三轴稳定，而是绕Z轴存在明显转动。

表2 对地指向仿真参数Table 2 Simulation parameters of Earth pointing

采用相同的轨道参数进行星体－Y轴对日指向模拟仿真，其初始仿真参数如表3所示。仿真结果如图6～9所示。

表3 对日指向仿真参数Table 3 Simulation parameters of Sun pointing

由仿真结果(图6)可知，对日指向误差在8500 s内收敛于3°以内。由图8可知，Y轴角速度(位于±0.2°/s之间)远大于另外两轴角速度(位于±0.02°/s之间)，说明星体大略沿Y轴转动。后又采用多组不同初始轨道参数与初始姿态，无论对日还是对地指向皆可获得较好的效果，进一步验证了本方法的有效性。

4 结论

本文针对单轴指向控制问题，提出了一种基于空间几何分析和仿射坐标变换的全新磁控算法。该方法简便易行，避免了磁控干扰力矩的产生，几乎不受轨道形状以及星体惯量积等因素制约，具有较强的工程实用价值。通过仿真对本方法进行了校验，仿真中采用惯量积非零的星体惯量阵，小倾角非圆轨道，以纯磁控实现了星体单轴对地或对日指向，仿真结果进一步验证了本方法的可行性。本方法的稳定性证明需要在后续工作中进一步完成。

［1］ 郭延宁.卫星姿态的磁控制方法研究［D］.哈尔滨:哈尔滨工业大学，2008.［Guo Yan-ning.Satellite attitude control methods using only magnetorquers［D］.Harbin:Harbin Institute of Technology，2008.］

［2］ 屠善澄.卫星动力学与控制(2)［M］.北京:中国宇航出版社，1998:283－289.

［3］ Fredrik S H.Optimal attitude control of a double cubesat using magnetorquers［D］.Trondheim: Norwegian University of Science and Technology，2011.

［4］ Wisniewski R.Linear time-varying approach to satellite attitude control using only electromagnetic acuation［J］.Journal of Guidance，Control，and Dynamics，2000，23(4):640－647.

［5］ Janardhana S，Mashuq U N，Pyare M T.Attitude control of magnetic actuated spacecraft using super-twisting algorithm with nonlinear sliding surface［C］.The 12th IEEE Workshop on Variable Structure Systems，Mumbai，India，January 12－14，2012.

［6］ Zhou B.Global stabilization of periodic linear systems by bounded controls with applications to spacecraft magnetic attitude control［J］.Automatica，2015，60(1):145－154.

［7］ Takaya I，Kentarou I，Junhwi B，et al.Interplanetary magnetic attitude control in small sized spacecraft［C］.2016 IEEE Aerospace Conference，Montana，USA，March 6－11，2016.

［8］ Chasset C，Noteborn R，Bodin P，et al.3－axis magnetic control:flight results of the TANGO satellite in the PRISMA mission［J］.CEAS Space，2013，23(5):1－17.

［9］ 张洪华，王芳.欠驱动挠性航天器的单轴指向控制［J］.宇航学报，2011，32(7):1491－1501.［Zhang Hong-hua，Wang Fang.Single axis pointing control for underactuated flexible spacecraft［J］.Journal of Astronautics，2011，32(7):1491－1501.］

通信地址:深圳市南山区科园路2002号卫星大厦425房间(518054)

电话:(0755)26994864

E-mail:kouyimin@126.com

(编辑:牛苗苗)

A Geometry Approach to Single Axis Pointing Control Using Only Electromagnetic Actuation

KOU Yi-min1，2，YUAN Qin1，JI Yan-bo1，ZHANG Ying-chun1，2
(1.Aerospace Dongfanghong Development Ltd.，Shenzhen 518057，China; 2.Department of Control Engineering，Harbin Institute of Technology，Harbin 150001，China)

A control strategy for single axis pointing of micro-satellites is proposed which uses only magnetictorquers.This method is useful in satellites'safe modes and other specific situations.It contains the following steps:firstly，a geometry algorithm is utilized to extend the collection of the rotation axis to a plane，along which the current and target directions can coincide;secondly，an angle acceleration plane is found by affine transaction from the perpendicular plane of the local geomagnetic field with the satellite's inertial matrix;thirdly，a controller that works along the intersecting line of the rotation axis plane and the angle acceleration plane is constructed to control both the rotating direction and the speed.Compared with the existing methods，this new method has advantages such as no additional disturbance from magnetic torque，less limitation from orbit shape as well as inertia products need not to be zero.The performance of the controller is validated in simulation，in which the Sun pointing and the Earth pointing with single axis are realized.

Micro-satellite;Single axis pointing control;Active magnetic control;Geometry analysis

V412.4

A

1000-1328(2017)01-0066-06

10.3873/j.issn.1000-1328.2017.01.009

寇义民(1980－)，男，博士，高级工程师，主要从事微小卫星姿控系统与星务数管系统研究。

2016-04-22;

2016-10-28