浅谈发散思维的培养

摘要：数学课程是培养公民素质的基础课程，在培养学生的创新思维方面具有其他学科不可比肩的作用，发散思维是创新思维的主要部分，一题多解与一题多变是培养发散思维的主要方法.

关键词：数学；发散性思维

作者简介：刘锦发（1969-），男，福建省武平县人，中学高级教师，主要从事中学教学研究.心理学家吉尔福特说过“人的创造力主要依靠发散思维，它是创造性思维的主要部分”，新课程标准要求通过新课程的学习，培养学生的创新意识，因此，培养学生的发散性思维就成了重中之重的任务.

一、一题多解培养发散思维

一题多解是从不同的角度、不同的方位审视分析同一题中的数量关系，用不同解法求得相同结果或把同一条件下隐含的结果都找出来.数学教学的目的不仅要求学生掌握好数学的基础知识和基本技能，还要求发展学生的能力，培养他们良好的个性品质和学习习惯.在实现数学教学目的的过程中，适当的一题多解，可以激发学生去发现和去创造的强烈欲望，加深学生对所学知识的深刻理解，训练学生对数学思想和数学方法的娴熟运用，锻炼学生思维的广阔性和深刻性、灵活性和独创性，从而培养学生的思维品质，发展学生的创新思维.

在几何学习中，一个动点往往导致图形的变化与结论的变化.

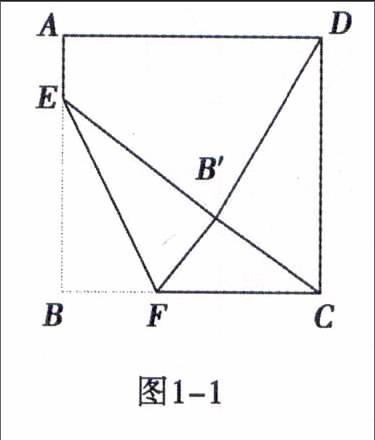
例1如图1，已知正方形ABCD的边长是16，点E在边AB上，AE=3，点F是边BC上不与点B、C重合的一个动点，把△EBF沿EF折叠，点B落在B′处，若△CDB′恰为等腰三角形，则DB′的长为.

解析根据题意，若△CDB′恰为等腰三角形需分三种情况讨论：

1）如图1-1，DB′=DC时，则DB′=16（易知点F在BC上且不与点C、B重合）；

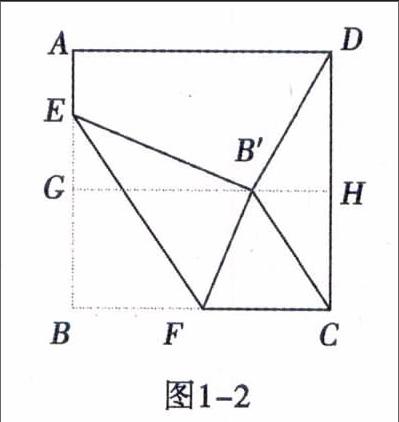
2）如图1-2，当CB′=DB′时，作BG⊥AB与点G，交CD于点H.

∵AB∥CD，∴B′H⊥CD，

∵CB′=DB′，∴DH=12CD=8，∴AG=DH=8

∴GE=AG-AE=5，

在Rt△B′EG中，由勾股定理得B′G=12，∴B′H=GH-B′G=4.

在Rt△B′DH中，由勾股定理得DB′=45.

（3）当CB′=CD时，∵EB=EB′，CB=CB′∴点E、C在BB′的垂直平分线上，∴EC垂直平分BB′，由折叠可知点F与点C重合，不符合题意，舍去.

综上所述，DB′=16或45.

从不同角度去思考问题，寻求解决问题的办法，也是培养发散思维的有效途径.

例2油桶包油重800克，用去一半油后油桶包油重450克，问油有多少克？

思路一从油的角度出发，设油x克，则由800-12x=450，解得x=700（克）.

思路二从桶的角度出发，设桶x克，则12（800-x）+x=450，解得x=100克，故油重为800-100=700（克）.

二、一题多变培养创新思维

教学中，立足于某一些基本条件，结合相关模块知识把条件或结论适当改变，变成新情景或新问题，要求我们能够立足基础，结合实际，调动思维，扩大思考范围，我们习惯称为一题多变.一题多变是培养学生思维灵活性与深刻性的重要手段，能使学生思维更具发散性.因此，在教学中要挖掘题目潜能，适当改造一些题目以拓宽学生思路、培养学生学习兴趣，提升学生探究能力

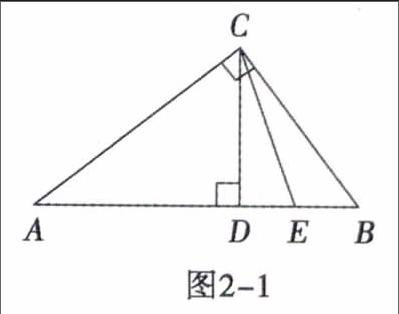
例3如图2-1，已知，RT△ABC中，∠ACB=90°，CD⊥AB于点D，CE平分∠BCD，求证：AE2=AD·AB.

解析∵△ABC是RT△，∠ACB=90°，CD⊥AB于点D.

∴∠ACD=∠B，AC2=AD·AB.

∵CE平分∠BCD.

∴∠DCE=∠ECB.

∴∠ACD+∠DCE=∠B+∠ECB.

∴AC=AE∴AE2=AD·AB.

变式一如图2-2，已知，RT△ABC中，∠ACB=90°，CD⊥AB于点D，AE平分∠BAC交BC于E，求证：CE∶EB=CD∶CB.

解析∵△ABC是RT△，∠ACB=90°，CD⊥AB于点D.

∴△ACB∽△ADC，从而AC∶AB=CD∶BC.

∵AE平分∠BAC交BC于E.

∴AC∶AB=CE∶EB.

∴CE∶EB=CD∶CB.

變式二如图2-3，已知，RT△ABC中，∠ACB=90°，CD⊥AB于点D，若∠DCB=∠BCE，求证：BD∶DA=CE2∶AE2.

解析∵△ABC是RT△，∠ACB=90°，CD⊥AB于点D.

∴AC2=AD·AB，BC2=BD·BA，

∴证明BD∶DA=CE2∶AE2可转化成证明BC2∶AC2=CE2∶AE2，进一步转化成证明BC∶CE=AE∶AC.

∵∠A=∠BCD.∠E是△EBC和△ECA的公共角 ∴△EBC∽△ECA.

∴BC∶CE=AE∶AC.

∴BD∶DA=CE2∶AE2.

一题多变不仅可以培养学生的发散思维能力及相关知识点迁移能力，还可以大大扩大学生的知识容量，经常做这种训练，不仅可以提高学生思维质量，还可以培养学生面对难题的良好的从容心态，也是一种良好的学习品质.

总之，在教学中多进行发散性思维训练，不只可以让学生掌握更多的解题方法，重要的是培养学生灵活多变的解题思路、提高教育教学质量的同时，为培养学生的创新意识立下基础.

参考文献：

[1]凡禹.纲与目——发散与收敛.超常思维的修炼[M].北京：民主与建设出版社.

[2]陈辉陆.培养学生发散思维能力的几点做法[EB].[2012-08-22].http：//www.docin.com/p-466993998.html

[3]宋建平.浅谈初中数学教学中学生发散思维能力的培养[EB].[2008-09-16].http：//blog.sina.com.cn/s/blog_50f9b68d0100ashp.html