织物弯曲性能测试新方法
季 慧, 蒋耀兴, 张长胜
(1.苏州大学 纺织与服装工程学院,江苏 苏州 215123;2. 现代丝绸国家工程实验室,江苏 苏州 215123)
研究与技术
织物弯曲性能测试新方法
季 慧1, 蒋耀兴2, 张长胜1
(1.苏州大学 纺织与服装工程学院,江苏 苏州 215123;2. 现代丝绸国家工程实验室,江苏 苏州 215123)
斜面法是测试织物弯曲性能最普遍的方法,但是斜面法本身有一定的局限性。针对这种情况,制作出了一种新弯曲性能检测仪,由自动送样装置和图像处理的软件程序两部分组成,来测试织物的弯曲性能,文中称之为新方法。分别测试了20种织物的弯曲性能,得到了两种方法的伸出长度读数,并用积分计算了弯曲状态下曲线的长度。结果表明:两种方法得到的伸出长度读数之间,积分算法得到的长度与伸出长度读数之间都具有高度线性相关关系,说明积分算法的结果可以表征新方法的伸出长度;两种方法的弯曲刚度之间相关系数的平方R2=0.970,为高度正相关,说明提出的测试织物弯曲性能的新方法是可行的。
织物;弯曲性能;测试方法;图像处理;斜面法
织物弯曲性能的测试方法有很多[1-3],如纺织品测试标准中的斜面法、悬臂梁法、心形法(GB/T 18318.4—2009)等。新方法如水滴法[4]、模拟仿真法、神经网络法[5]等,其中斜面法因其操作简单、评价指标明晰而成为纺织服装界应用最广泛的测试方法[6]。但是,斜面法更多依赖于人为操作,会受人的心情、环境、视力影响造成误差。其次,斜面法对特别柔软、轻薄的织物很难测试,有一定的局限性。除此之外,斜面法只能得到织物的伸出长度,并不能得到最终的弯曲形态[7]。基于这一现状,本文设计了一种新弯曲性能检测仪,它由自动送样装置和基于C++及OpenCV图像处理技术的软件程序组成,也就是本文所说的新方法。
1 实 验
1.1 材 料
材料:选取了棉、麻、丝、毛、化纤织物共20种,尺寸为25 mm×200 mm,编号分别为1#~20#,织物基本参数见表1。
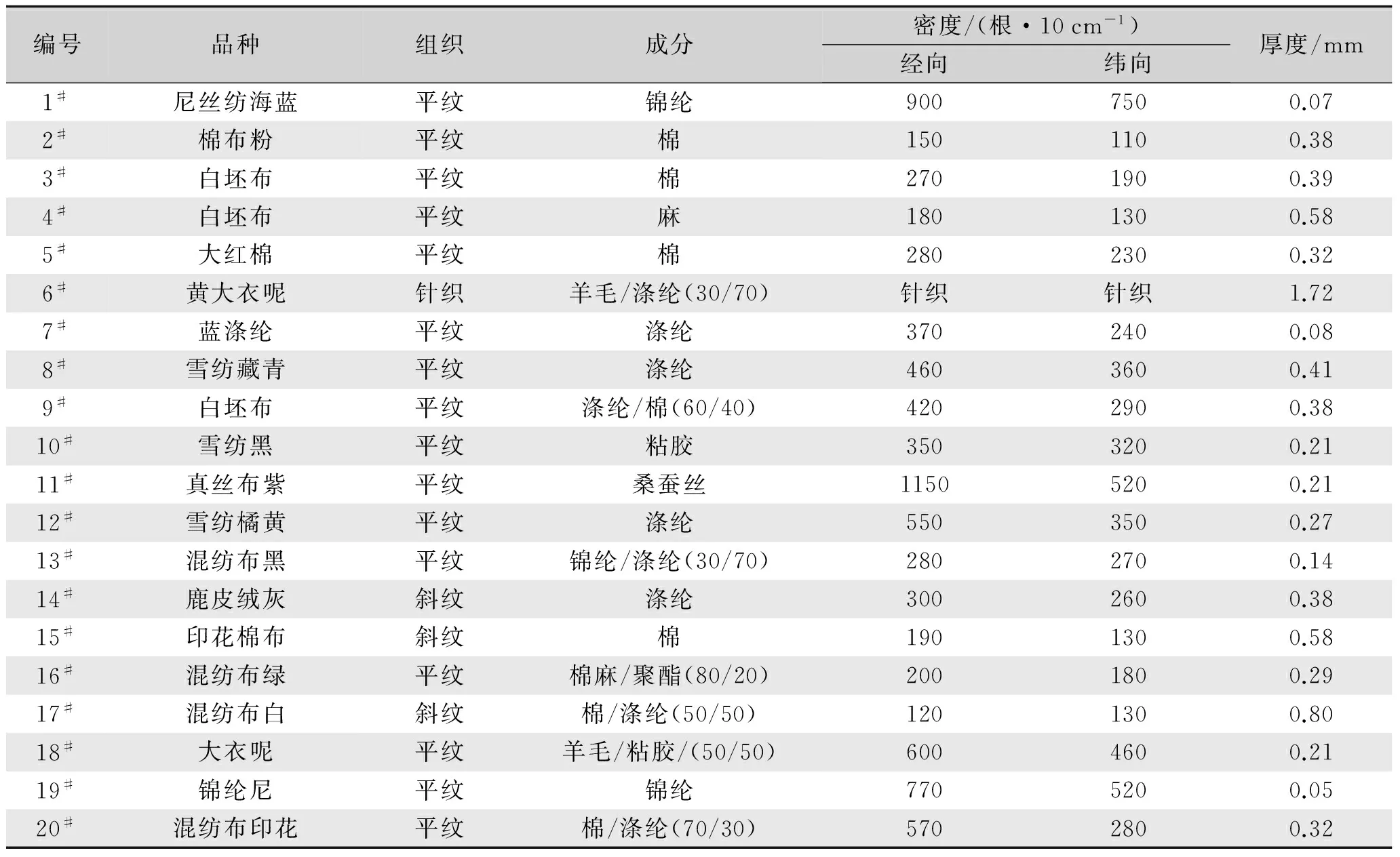
表1 织物基本参数
1.2 方 法
本文设计了一种新弯曲性能检测仪,它由两部分组成,一是其自动送样装置,二是软件程序。
1.2.1 原 理
该方法的原理与斜面法相似,但获取弯曲长度的途径不同,斜面法是通过人眼读数,新方法则是将微距摄像头固定于装置短轴一端,试样弯曲的过程会同步在电脑程序中。当试样弯曲到45°时,程序自动获取这一帧图像,之后自动再计算出其弯曲形态的长度,即伸出长度,该长度的一半就是弯曲长度。
1.2.2 自动送样装置
一种织物弯曲性能的自动送样装置:水平装置及水平装置上的平面、压板、H型电动推动杆和小钢块(图1)。
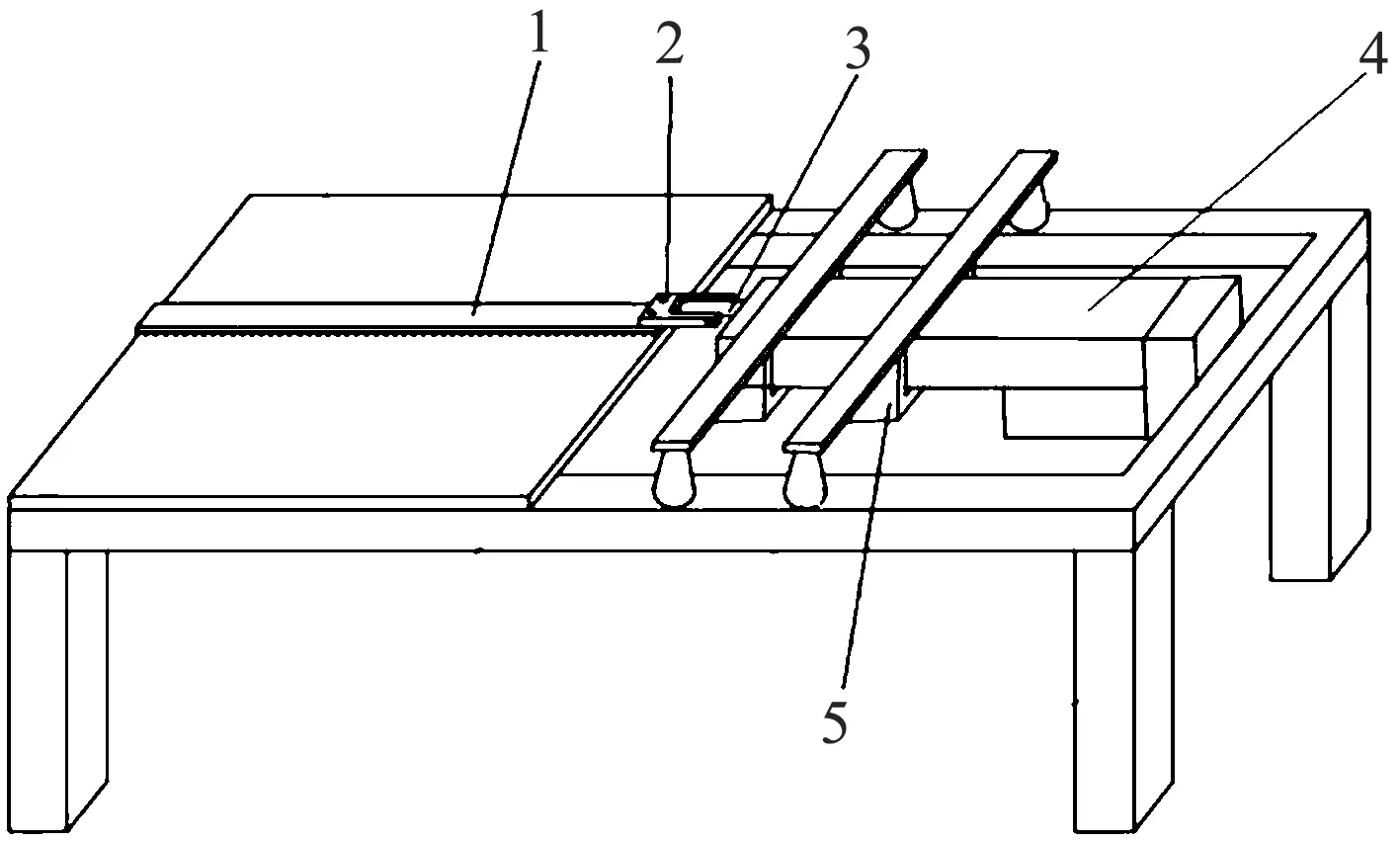
1.压板,2.小钢块,3.H型电动推动杆头部,4.H型电动推动杆,5.固定塑胶图1 自动送样装置Fig.1 Diagram of automatic sample conveying device
其特征在于:
1)装置由4个立柱支撑高出桌面160 mm,装置宽度为200 mm,长度为550 mm,总质量为4 kg,所占空间较小,轻便易于移动,方便随时测试。
2)平面为不锈钢板,宽度为200 mm,长度为300 mm,厚度为1 mm,表面光滑、分布均匀,用于放置试样。
3)压板为铝板,宽度为30 mm,长度为280 mm,厚度为6 mm,用于带动试样运动。压板的质量为100 g,若压板过重会损伤试样,若压板过轻不易带动试样,所以选择该质量较为适当。压板的底面黏有一层厚度为1mm的波浪型橡皮,增加摩擦力,方便较为厚重试样的送样,压板放置在平面上能维持底面平衡,不会晃动。因是波浪型橡皮,压着试样时,与试样接触留有空隙,不会出现运动时因摩擦力过大,致使试样黏着压板不落下或突然落下的情况。压板的侧面标有刻度,方便获取读数。
4)H型电动推动杆行程为150 mm,速度为10 mm/s,头部突出部分为20 mm,用于推动试样。通常试样推出150 mm即已形成弯曲状态,足以获得实验相关指标。推动150 mm人为推动需要17 s,该推动杆推动需要15 s,即人推动试样的速度约为9 mm/s,该推动杆的速度10 mm/s,与人推动速度最为接近。综上所述,所以选择了该电动推动杆。
5)小钢块宽度为30 mm,长度为45 mm,厚度为8 mm,后端为U型,用于连接压板与H型电动推动杆。
H型电动推动杆参数:品牌为三拓;名称为H型电动推动杆;电压为DC 24 V 20 VACE;行程为150 mm;速度为10 mm/s。
1.2.3 软件部分
本文是运用C++和OpenCV结合的方法对图像进行处理[8]。图2中白色区域部分与平面成45°。

图2 初始帧Fig.2 The initial frame
通过每一帧中白色区域像素值与初始帧中该区域的像素值比较得到目标图像,如图3所示;经过图像剪切、滤波、细化后再拟合曲线,得到最终的弯曲形态图,如图4所示。最后,根据拟合曲线得到弯曲形态的曲线方程,利用弧积分公式求得伸出长度。

图3 目标帧Fig.3 The target frame

图4 弯曲形态Fig.4 The bending form
1.3 实验准备及评价方法
1)工具:送样装置、微距摄像头、电脑、背景板和其他。
2)条件:在GB/T 6529—2008《纺织品 调湿和试验标准大气》规定标准大气、光照均匀、光线充足且无风的室内。
3)试样:上述20种试样按经向、纬向两个方向剪成25 mm×200 mm大小,分正面和反面,每种情况试样剪3块。
评价方法与斜面法相同。
2 结果与分析
2.1 伸出长度的有效性分析
斜面法测得的伸出长度为I0,新方法中根据图像读数得到的伸出长度为I1,根据积分计算得到的伸出长度为I2。
2.1.1 研究新方法伸出长度读数有效性分析
图5为采用斜面法与新方法测得的20种试样伸出长度读数的散点图。由图5可见,两种方法测得的伸出长度呈显著的线性关系[9]。
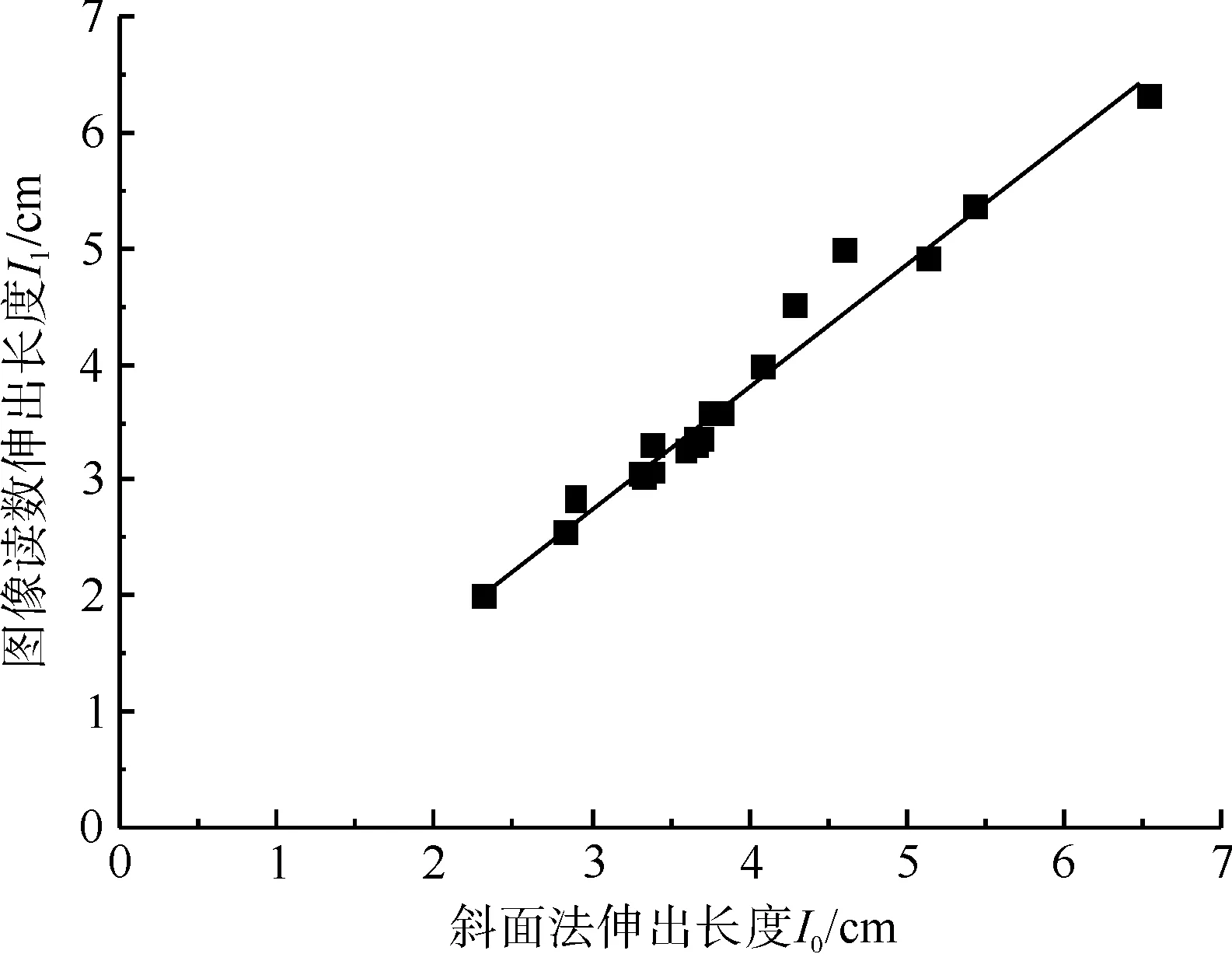
图5 两种方法伸出长度读数散点分布Fig.5 Scatter diagram of overhanging length readings by two methods
回归分析后,可知两者的相关系数的平方R2=0.968,回归方程为:
(1)
F检验值为553.426,其显著性小于0.001,说明回归方程非常显著。t检验值为23.525,其概率p值小于0.001,说明回归系数非常显著。由此可见,这两种方法测得的结果具有可替代性,新方法是可行有效的。
2.1.2 新方法积分算法的有效性分析
图6为新方法中根据图像读数得到的伸出长度I1与根据积分计算得到的伸出长度I2的散点图。
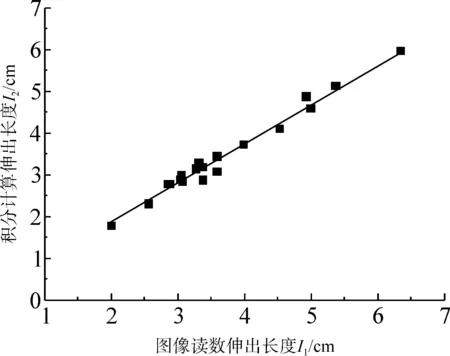
图6 图像读数与积分计算测得伸出长度散点分布Fig.6 Scatter diagram of overhanging length by image reading and integral calculation
回归分析后,可知两者的相关系数的平方R2=0.980,回归方程为:
(2)
F检验值为901.150,其显著性小于0.001,说明回归方程非常显著。t检验值为30.019,其概率p值小于0.001,说明回归系数非常显著。这表明,积分算法的结果与图像读数具有高度一致性,积分算法是切实有效的。
积分算法计算弯曲形态曲线得到的曲线长度可作为新方法的最终伸出长度,因为它具有非常高的准确性。
2.2 伸出长度的误差分析
2.2.1 两种方法伸出长度读数的误差分析
1)压板误差。斜面法使用的是钢尺做压板,钢尺与试样是完全接触,若是较薄的试样,容易在推出过程中会黏着钢尺不能自然落下,若是较厚重的试样,容易因摩擦力不足造成钢尺运动时试样未运动的情况;新方法使用的是底面黏有一层波浪型橡皮的铝板做压板,因底面是波浪型,压板与试样接触时留有空隙,在实验过程中即使试样再薄也未曾出现过试样黏着压板的情况,若是试样较厚重,橡皮的摩擦力要大于钢尺,出现钢尺运动而试样未运动的误差也较斜面法要小些。
2)推动误差。斜面法是人为推动,难免会出现推动时受力不均、手抖动的情况;新方法使用的是速度为10 mm/s的H型电动推动杆,推出速度接近于人为推动速度9 mm/s,全程均匀推动,不会出现受力不均、手抖动、试样推歪的情况。
3)位置判断误差。斜面法位置判断主要通过人眼,而且等待几秒至弯曲形态稳定。新方法位置判断是通过程序,而且其弯曲形态是一瞬间形态,即是第一次到45°时的形态,不是其稳定下来的形态。
4)试样误差。对于针织物而言,不太适合用斜面法和新方法测试。图5中间区域有两个误差较大的,其中一个就为6#针织物,另一个为4#麻布。4#麻布出现较大误差,可能是因为它的厚度不太均匀。除此之外,实验中发现斜纹试样的卷边现象较严重,会造成两种方法的位置判断误差较大。
5)环境误差。两种方法都要求在温度为20 ℃,相对湿度为65%的标准大气环境下进行,但新方法对环境的要求更为严苛,它还需要光照均匀、光线充足且无风的环境,否则会造成较大误差。
2.2.2 新方法读数与积分算法的误差分析
1)压板误差。无论斜面法还是新方法的图像读数法,都很有可能在推动过程中或多或少地出现因摩擦力不足造成压板运动试样未运动的现象,这样会导致测得的伸出长度大于实际伸出长度。如图6所示,图像法读数均比积分算法得到的伸出长度略微大。而用积分算法,则与其压板伸出的长度无关,只记录其弯曲形态从而计算,减小误差。
2)噪声点误差。虽然图像滤波已经除去大部分的噪声点,但还是可能存在一两个微小的噪声点,在拟合曲线的过程中造成小误差。
3)算法误差。算法中途都会使用四舍五入得出中间结果,导致最后结果已被四舍五入多次,会造成微小误差。
2.2 两种方法的弯曲刚度回归分析
对采用两种方法测得的20种试样弯曲刚度做了回归分析,结果如图7所示。斜面法和新方法测得的弯曲刚度结果分别对应B1、B2。
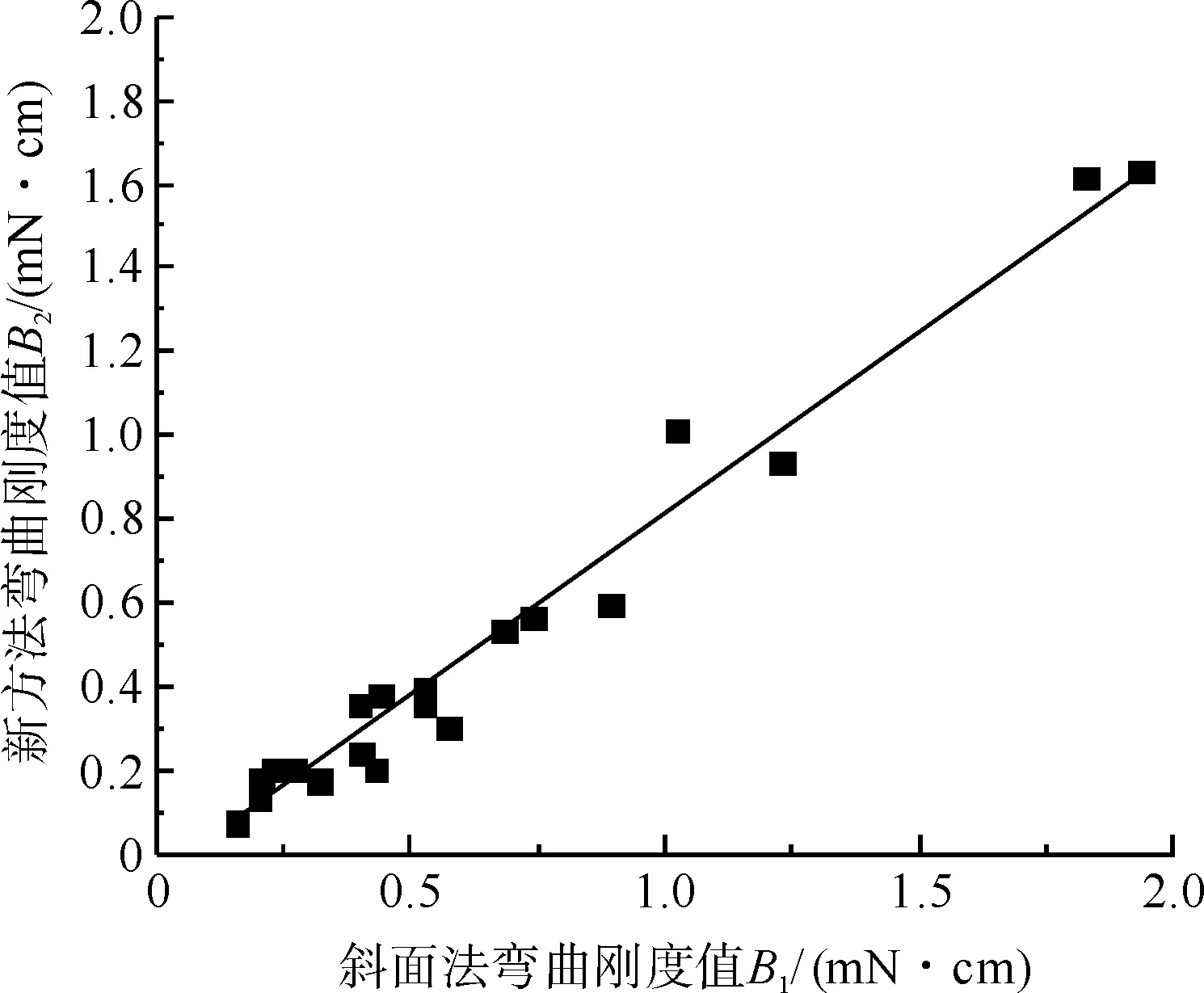
图7 两种方法弯曲刚度散点分布Fig.7 Scatter diagram of bending rigidity by two methods
两者之间的相关系数的平方R2=0.970,呈高度正相关,对应的回归方程为:
(3)
F检验值为618.754,其显著性小于0.001,说明回归方程非常显著。t检验值为24.875,其概率p值小于0.001,说明回归系数非常显著。也就是说,本测试方法与传统斜面法测得的弯曲刚度一致性较高,可以用该方法来表征织物的弯曲刚度。
3 结 论
1)本文的新方法虽然原理与斜面法相似,但大幅减少了人力操作,只需实验人员将试样放置于压板下,按下H型电动推动杆开始按钮,打开电脑中程序,即可获得弯曲过程中的实时图像,能自动检测出45°时的目标帧,并自动进行计算。
2)将两种方法得到的弯曲刚度进行回归分析,得到R2=0.970,说明该检测方法是有效的。
3)对两种方法得出的伸出长度进行误差分析。由图5可知,斜面法得到的伸出长度往往要大于新方法,误差主要来源于装置本身、试样及环境。由图6可知,积分法得到的伸出长度往往要小于图像读数,误差主要来源是压板、噪声点及四舍五入算法。
4)积分法还存在一些微小噪声点的问题,将尝试在程序初始而不是中途就加入滤波程序再看效果。
5)该方法虽然能得到织物弯曲过程中的每一帧图像,但是对于图像的分析还仅限于45°时刻的图像,只能得到静态织物弯曲性能。下一步将再改进程序,得到更多角度的图像分析,为研究动态织物弯曲性能奠定基础。
[1]杨萍,于伟东.纱线和织物的弯曲刚度[J].毛纺科技,2002(1):8-12. YANG Ping, YU Weidong. Bending rigidity of yarn and fabric[J].Wool Textile Journal,2002(1):8-12.
[2]GHOSH T K, ZHOU N. Characterization of bending fabric bending behavior: a review of measurement principle[J]. Indian Journal of Fabric & Textile Research,2003(28):471-476.
[3]石风俊,胡金莲,余同希.织物折皱弯曲性能的研究[J].纺织学报,2000,21(1):11-13. SHI Fengjun, HU Jinlian, YU Tongxi. Research on wrinkle and bending performances[J]. Journal of Textile Research,2000,21(1):11-13.
[4]刘成霞,韩永华,张才前.基于图像处理的织物弯曲性能测试方法[J].纺织学报,2013,34(7):52-56. LIU Chengxia, HAN Yonghua, ZHANG Caiqian. Test method for fabric bending behavior based on image processing[J]. Journal of Textile Research,2013,34(7):52-56.
[5]孙炳合,梅兴波,王正伟.织物弯曲性能研究的动态和新方法[J].上海纺织科技,2000,28(3):7-8. SUN Binghe, MEI Xingbo, WANG Zhengwei. Developments and new methods of bending property of fabric[J]. Shanghai Textile Science & Technology,2000,28(3):7-8.
[6]吴巧英,胡滢,吴春胜,等.不同织物弯曲性能测试仪测试结果的比较[J].纺织学报,2015,36(7):126-130. WU Qiaoying, HU Ying, WU Chunsheng, et al. Comparative analysis on test results of different fabric bending behavior test apparatus [J]. Journal of Textile Research,2015,36(7):126-130.
[7]何琦辉,王正伟.利用织物实际弯曲形态测试其弯曲性质的算法[J].纺织学报,2006,27(12):52-58. HE Qihui, WANG Zhengwei. Arithmetic of bending property of the fabric based on its actual bending shape[J]. Journal of Textile Research,2006,27(12):52-58.
[8]蒋东升.基于数学形态学的边缘检测算法的研究[D].成都:电子科技大学,2012:9-12. JIANG Dongsheng. Study of Edge Detection Based on Mathematical Morphology Algorithm[D]. Chengdu: University of Electronic Science and Technology,2012:9-12.
[9]薛薇.SPSS统计分析方法及应用[M].北京:电子工业出版社,2007:137-162. XUE Wei. SPSS Statistical Analysis Methods and Applications[M]. Beijing: Electronic Industry Press,2007:137-162.
A new test method for fabric bending behavior
JI Hui1, JIANG Yaoxing2, ZHANG Changsheng1
(1. College of Textile and Clothing Engineering, Soochow University, Suzhou 215123, China; 2. National Engineering Laboratory for Modern Silk, Suzhou 215123, China)
Incline method is the most common method used to test the bending behavior of fabrics, but it has some limitations. Aiming at this, a new bending test instrument called a new method was made in this paper, which is composed of two parts, the automatic sample conveying device and the image processing program. The bending behaviors of 20 fabrics were tested respectively, and the readings of overhanging length were gained. The length of the curve under bending condition was figured out with integral. The experimental result shows that the readings of two methods, the results of integral calculation and the readings of the new method have high linear correlation. This indicates that the results of integral calculation can represent the overhanging length of the new method; the square of bending rigidity correlation coefficient of two methods isR2=0.970, high-positive correlation. This shows the new method is feasible.
fabric; bending behavior; test method; image processing; incline method
I1=-0.347+1.049I0
I2=-0.036+0.952I1
B2=-0.78+0.890B1
10.3969/j.issn.1001-7003.2017.03.006
2016-07-13;
2016-12-28

TS101.923
A
1001-7003(2017)03-0033-05 引用页码: 031106

