大学物理和场论课程中的协变性浅谈

王雯宇 王丝雨 许 洋

(北京工业大学应用数理学院，北京 100124)

教学研究

大学物理和场论课程中的协变性浅谈

王雯宇 王丝雨 许 洋

(北京工业大学应用数理学院，北京 100124)

本文主要论述了物理量的协变性质在大学物理和场论教学中的重要性。 首先以图示的办法形象地讲解电磁场的洛伦兹变换，同时指出协变性的理解可以使学生更加深刻理解电磁学理论的本质。论文证明n阶反对称张量在行列式为1的矩阵变换下是不变的， 因此四阶反对称张量εμ νρ σ自然是协变的， 矢量和轴矢量的镜像变换性质是不一样的。 论文还指出协变性是对物理公式变换性质的表述，物理量会因为形式不同而有不同的协变性的理解。论文以场论散射截面的协变性质为例， 指出不同理解的差别与联系。

协变性；电磁场的变换；反对称张量；散射截面

1 提出问题

对称性是物理学研究的一项重要内容。根据诺特尔定理[1]，每一个连续的对称性都有一个守恒流与之对应。 因此当我们发现了一种对称性之后，就意味着找到了一个守恒量，从而揭示了一个深刻的物理规律。 对称性如此重要，以至于当我们研究一个物理系统或构建一个物理模型的时候，对称性是首要考虑的， 在写一个公式或方程时，往往又要求公式写成协变的形式。所谓的协变形式即物理量按照其相应的对称变换形式来表述。比如某物理量是一个矢量，就意味着该量既有大小，又有三维空间的指向，同时按照三维空间的旋转操作变换。因其三维空间的矢量而具有的深刻物理性质并不仅仅是有大小有方向那么简单， 三维空间旋转协变性质决定了其大部分的物理性质。如果一个方程以若干矢量来表述，方程两边都是矢量运算，那么这个方程自然是空间旋转不变的，该物理系统也就是一个三维空间旋转协变的系统。 在物理学教学中，对称性对于物理学的重要性以及物理量协变性质应该向学生做深入的讲解， 才能使学生深刻理解物理学的本质。

本文以物理量的协变性质为主题，以大学物理和场论教学中的两个例子来阐示协变性质讲解的重要性。 首先作者以实际课堂经验为基础，说明如何在电磁学最后一次课中讲解电磁场的协变性质， 进而使学生初步理解电磁学理论的对称性质。第二个例子是在场论的教学中n阶反对称张量协变性质的证明。在通常的教科书上，n阶反对称张量是直接引入的， 而张量有确定的协变性质，所以对于一个常数是否可以称为张量是需要证明的。 这一点作为场论教学的基础知识点需要补充。在量子场论的研究中，一个重要的物理量是粒子散射截面， 该量的协变性质不同的物理学家有不同的理解。本文简单说明理解的异同，并说明如何以较为开放的态度来理解一个物理量的协变性质。

本文作以下安排：第2节以两个典型协变性的案例分析来说明协变性质的重要性；第3节说明如何表述协变性并分析粒子散射截面的协变性； 第4节给出本文的总结。

2 两个协变性案例分析

2.1 电磁场协变性质补充

当前大学物理电磁学课程通常从静电学开始，随后讲授磁场，电磁感应，最后以麦克斯韦方程组结束。 这实际上是经典电磁学的内容[2]，因为狭义相对论已经在力学部分讲授过，所以电磁学课程通常不再包含相对论的内容。但是在相对论课程中，一般都会提到电磁场满足洛伦兹变换， 这是狭义相对论课程的重要基础知识之一。如果在电磁学课程结尾处不做回应的话，课程体系有失完整，因此在电磁学最后一课安排20分钟简单讲解电磁学的狭义相对论理论是必须的。而在这样短短的时间内完成这个任务是困难的。作者根据实际课堂讲授经验，发现以一个静止点电荷为例，围绕静电场的洛伦兹变换展开讲述有着不错的效果。而协变性概念的讲解尤为重要。如果学生从讲解中加深了力学中已经得到的协变性的理解，就可以认为讲课达到了理想的效果。下面简述一下讲课思路，让学生考虑一个静止的电量为e的点电荷在空间中形成的库仑场。若电荷附近有观测者乘火车匀速通过，询问观测者看到的还是不是一个静电场；如果不是，火车上的观测者看到的现象与相对点电荷静止的观测者看到的静电场有什么关系。接着指出根据运动电荷的毕奥-萨伐尔定律可以计算空间中还分布着磁场。然后利用图1 来说明不同参考系的观测者看到的是同一种物质：电磁场。电磁场构成了协变张量Fμ ν[3]:

(1)

图1 形象图示电磁场不同参考系之间变换

在这里简单说明张量的定义及性质：张量就是按照时空对称性变换的量。标量是变换不变的量； 矢量是一阶张量，有大小，有方向，用洛伦兹变换矩阵变换；更高阶的张量可以带更多的指标， 每个指标的变换都遵循时空对称变换规律。这么解释当然不够浅显易懂，那就指出电磁场张量就类似于图1中二维空间某矢量A，电场和磁场类似于矢量A在不同坐标轴上的投影，一个类比电场强度E，另一个类比磁感应强度B，变换参考系相当于选取不同的坐标系。 如在图1(a)中由实线坐标系变换到虚线坐标系的时候， 坐标轴上的坐标进行二维平面旋转变换即可得到不同坐标系下每个分量的变换关系。 当参考系合适时，如图1(b)，某个分量坐标为零，对应磁感应强度为零， 这正是静止点电荷的情形。

下面可以给出Fμ ν的洛伦兹变换的具体形式:

(2)

(3)

最后用变换之后的电场和磁感应强度：

(4)

与库仑场进行对比，并说明图1只是个形象的表示，真正的变换是以公式(2)来进行的。这样虽然时间较短，但是可以把电磁学与力学作一次较为完整且简单的联接。

不仅如此，大多数非理论物理专业人士可能并不能深刻理解协变性质的重要性。正如引言中所说， 当我们定义某物理量时，其相应的协变性质已经决定了该物理量的大部分物理性质。这些性质并未为大多数人所理解，以至于必须以“定律或定理”的形式加以明确。一个典型的例子就是电磁学的相对论理论。从理论上讲如果已经知道了力学的相对性理论，那么把质点力学理论推广到四维平直时空的场论，则一个四维矢量场Aμ(x)的模型应该是什么样的呢？其实四维时空的对称性就决定了Aμ的拉格朗日量最简单的形式(动能项加一个外源场)为

(5)

Fμ ν是公式(2.1)所述电磁场张量也是Aμ的动能项即场强：

Fμ ν=∂μAν-∂νAμ

(6)

jν(x)为四维电流源场。(这里不考虑有磁单极存在的情况，磁单极情况请参阅文献[4]) 利用变分原理可以得到Aμ的运动方程：

∂νFμ ν=μ0jμ

(7)

这实际上只是麦克斯韦方程组的两个方程：

而麦克斯韦方程组的另外两个方程：

其实就是四维时空矢量场的协变性质(与具体是什么场无关)决定的一个恒等式：

∂λFμ ν+∂μFν λ+∂νFλ μ=0

(12)

数学家一定很奇怪物理学家竟然把一个恒等式作为一个基本定律写入理论！ 如果人们深刻理解了协变性，那么电磁学相对论理论基础就是四维相对论时空矢量场论。麦克斯韦方程组则是该基础之上的动力学方程以及一个由协变性质决定的恒等式了。 当选定某个参考系，分开来看四维矢量场的Aμ(x)分量：

Aμ=(φ,A)

(13)

φ(x)为标量场，A(x)为矢量场。三维空间的协变性质决定了恒等式：

此即静电场的环路定理和磁场的高斯定律。若学生可以从这个角度理解电磁学， 则对电磁理论就有了更加深刻的理解，也为后续的量子电动力学等前沿理论的学习做好了铺垫。

2.2n阶反对称张量的协变性

事实上，一提到“协变性”的概念大家可能首先想到的是相对论，这是因为力学和 (有以太存在的)电磁学都是完备理论，相对论理论关键点在于要求力学和电磁学满足四维时空变换的对称性，因此协变性贯穿相对论始终。在此基础上，我们也明白了牛顿力学方程是三维空间协变的，现代量子场论中时空对称性和规范对称性是理论的第一要求。当构建一个满足某种对称性的模型时， 方程往往被要求写成协变形式，而张量形式是实现这一要求的有力数学工具。 大家可以看到麦克斯韦方程组公式(8)～公式(11)方程的时空变换性质不是明显的，而与之等价的公式(7)和公式(12)方程则是明显协变的， 这就是因为两个公式等号两边都是四维协变的张量。

现在的问题在于，像一阶张量(矢量Aμ)或二阶张量(Fμ ν)因为其分量为变量，因此其性质可以由变换性质来声明而不会出现问题。 但是在狭义相对论理论里有两个常数张量度规张量gμ ν和四阶反对称张量εμ νρ σ都满足四维时空的洛伦兹协变性。 这不是明显的，因为这两个张量的每个分量都是常数，如果对其做任意的洛伦兹变换仍然要保持其为常数看上去似乎不合理。gμ ν的协变性质容易理解，因为它的协变性实际上是洛伦兹对称性的定义要求的。光速不变原理要求时空间隔不变：

(16)

很容易得到：

(17)

这就是度规张量的协变性质。而反对称张量εμ νρ σ的协变性质在很多教科书上都一笔带过，或者甚至不提，直接就作为一个背景知识用作协变张量了。 下面给出一个简单的证明，以方便读者教学使用。

n阶全反对称张量εα1α2…αn又被称为Levi-Civita张量。它是由常数组成的矩阵，主要性质为： 任意两个指标交换，它的数值改变符号；任意两个指标相等，值为零。可以约定：

ε01…(n-1)=1

(18)

则n阶Levi-Civita张量可表示为

(19)

偶排列的意思是α0α1…αn-1任意两指标交换改变偶数次得到01…(n-1)的排列，奇排列亦然。

其实Levi-Civita张量在任意一个行列式为1的变换矩阵(幺模)变换下都是不变的。 我们考虑一个行列式为1的n×n矩阵A，行列式的计算可以表示为

(20)

此时我们假定εα0α1…αn-1按照矩阵A变换即：

(21)

由公式20自然有关系：

(22)

实际上由此关系就可以得到εα0α1…αn-1的全部性质。如ε′0…(n-1)上任意的两个指标i,j进行交换

(23)

(24)

这实际上是行列式的性质之一：矩阵的两行或者两列交换行列式反号。 所以εα0α1…αn-1的指标全部不同的情况就与公式(19)的要求相同了。

下面看εβ0β1…βn-1指标中有任意的两个指标相同的情况， 比如βi=βj，则矩阵A的变换

(25)

这其实是把矩阵A中一行(列)作为两行(列)来进行行列式计算， 行列式计算中若有两行(列)相同，线性相关结果为零。 这样就得到Levi-Civita的全部性质：

(26)

以上证明也可以让我们理解二阶三阶反对称张量εij，εijk的协变性质，比如三阶反对称张量可以方便地说明矢量积的矢量性质。两个矢量的矢量积也是一个矢量，如：

C=A×B

(27)

矢量C的大小为

(28)

C的方向与A、B的方向满足右手螺旋准则。 如果要从这个定义出发来证明C满足矢量的协变性质是不容易的，因为这需要证明C和A、B满足同样的三维空间旋转变换的性质。但是如果用三阶反对称张量把矢量积写成协变形式：

Ci=εijkAjBk

(29)

(公式中对j,k指标求和。)由三阶反对称张量的协变性质我们就对C的性质非常清晰了。不仅如此，εijk也给了一个很好的工具来表述三维空间的手征性质。 这一点大多数教科书其实是较少涉及的，即严格地说，如果A、B是两个矢量，则C是一个轴矢量。矢量和轴矢量的区别在于空间的镜像(宇称) 变换性质。空间作一个分立变换

r→r′=-r

(30)

两种矢量的变性质换是不一样的，如图2。图中间虚轴是对称轴，从图上可以看出矢量A的变换为

A→A′=-A

(31)

图2 矢量和轴矢量的镜像变换

轴矢量C的变换为

C→C′=C

(32)

即A的宇称为负，而C的宇称为正。这个变换性质很容易从轴矢量C的定义公式(29)中看出来。由此可知牛顿力学的基本动力学方程是一个矢量方程：

(33)

角动量动力学方程是一个轴矢量方程：

(34)

其中L是角动量，M是力矩。 联立这两个动力学方程把牛顿力学按照手征性质写为一个方程组:

注意公式中1/r是为了配平量纲。公式(35)可以定义为右手方程，它的镜像变换为公式(36)左手方程(定义)，反之亦然。若只取其中一个方程， 则得不到牛顿力学的基本方程，而且宇称也不守恒了。 理解这一点对同学以后理解量子理论中弱相互作用宇称不守恒等现象是很有帮助的。这是一个简单的反对称张量应用的例子，n阶反对称张量在理论物理高级课程中的还有其它的重要应用，这里就不细述了。

3 物理公式的协变性

本质上讲，没有“物理量”协变不协变的说法，而应该是“公式形式”是不是协变形式的问题。因为在某个理论框架内研究某个“物理量”，这个物理量在任何参考系的变换下都会按照该理论框架的基本变换性质变换，所以都是协变的。比如说在相对论理论中，能量、 动量等物理量都有相应的洛伦兹变换性质，单纯问“能量是否协变”是不合适的，而应该问某公式是否具有协变形式。因为任意非协变形式的公式原则上都可以写成协变形式， 而且可以写成不同的协变形式。比如两个粒子有动量:

(37)

(38)

(39)

也许有读者对任意形式的物理量都可以写成协变形式表示怀疑。 下面这个例子更加可以说明问题。现在来计算一个明显不协变的物理量： 粒子动量PxPy之和：

Px+Py

(40)

这是一个明显不协变的量，但是可以找到两个协变矢量:

在该参考系下:

(43)

则Px+Py可以写为

(44)

也是协变形式，当然也可以找到其他协变形式。所以原则上只要在某个理论框架下计算若干个物理量， 都可以写成协变形式，讨论某个“物理量”是否协变的意义不大。

以上的讨论虽然简单，甚至近似于诡辩，但是在处理具体的物理问题上， “物理量”的协变性与“物理公式”形式的协变性往往会引起人们的混淆。 物理量如果写成协变形式则说是协变的，如果不明显协变，则说不是协变的。 因此同样的一个计算过程可能会因为计算的表述形式不一样，得到了完全不一样的协变性的解释。 量子场论中对于散射截面的协变性理解就是一个明显的例子。 高能物理中一个重要的物理量就是粒子的散射截面，粒子散射是这样一个过程： 一个速度为va的粒子a(粒子流a约化为一个粒子。) 和一束流速为vb横截面积为A的粒子流b在一条直线上 (Z轴)发生碰撞，如图3。单位面积上在δt时间内粒子间发生相互作用的可能性δP正比于与a粒子碰撞的b粒子数目，即

(45)

图3 沿z轴粒子流a和b的对撞

其中,nb是b粒子的数密度;σ是比例系数。把b粒子也约化为一个粒子，然后把比例系数σ提取出来定义为粒子散射截面。它表示单位时间内单位面积上发生一个粒子散射过程的概率。 比如一个a+b→1+2+…+n的过程，具体截面σ的计算公式为

(46)

(47)

这个因子被称为流因子。对于流因子的协变性质不同是场论教科书给出了不同的回答。 比如国内比较流行的Peskin的《量子场论导论》[5]一书中就明确表明截面σ不是洛伦兹不变的，而仅仅是沿对撞轴Z轴平动不变。这看上去也很合理，因为截面是面积的量纲，做洛伦兹平动当然会因尺缩效应而改变。流因子F的形式为

(48)

εμxyν正是上文所计算的四阶协变全反对称张量。因为第2、3指标只取x,y分量，F当然不是协变的。 但是在剑桥大学出版社出版的《现代粒子物理》[6]一书中就明确说明F是洛伦兹不变的， 并给出了严格的证明，即写成了协变形式。为了明确启见，这里给出详细的推导过程。

(49)

则

(50)

因为

(51)

把上式中2EaEbPaPb代入公式(50)可得

因此流因子F可以写为

(52)

这是协变的。注意这里并没有说仅沿对撞轴Z轴平动协变。那到底是谁错了？抑或都对？

正如上文所述，任何物理量都可以写成协变形式。所以关于散射截面σ协变与否就有了不同的解释，而在实际的物理研究中往往大家关注的都是沿着对撞轴的洛伦兹变换， (由质心碰撞参考系变换到靶粒子参考系。)所以二者虽然结论不一样，但并不影响最终的物理结果。但是因为截面这个物理量如此重要， 在此文中，必须明确其协变性质。不妨定义一个物理量为

(53)

显然Πμ ν是协变的，而F=Πxy仅是Πμ ν的一个分量， 当然不是明显协变的。Peskin因此说F=Πxy是明显不协变的。 但是Πμ ν的其他分量(非Πxy,Πyx分量) 在以z轴为对撞轴的过程中(Px=Py=0)均为零。 这就类似于2.1节所述的对于静止点电荷的电磁场张量磁感应强度分量为零的情形。所以Πxy可以加上Πμ ν的其他所有的零分量写为协变形式

(54)

读者可以验证上式就与公式(52)一致了。所以对于截面σ的协变性的讨论， 我们应只讨论其形式的协变性，沿z轴平动，才可以说散射截面是协变的。 图4以直观的方式来说明差别：如同我们要研究矢量A和B组成的平行四边形的面积。可以定义的量是

(55)

或者

(56)

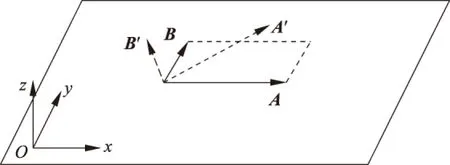
图4 矢量积和面积的计算

如果A和B仅在xOy平面内旋转则两种定义的计算结果是一样的， 如果在整个空间做任意的旋转，则计算结果明显不同。关于这个四边形面积协变性的表述则因为定义的不同而有不同的理解。 从2.1节静电场的洛伦兹变换和散射截面的案例可以看出，当一个协变形式的张量某些分量为零的时候，特别容易引起该量是否协变的争议。 这一点在电磁学和场论课堂上加以说明，可以加深学生对协变性质的理解。

4 结论

本文以物理量的协变性质为主题，以大学物理和场论教学中的两个例子来阐示协变性质讲解的重要性。 第一个案例中，论文用图示的办法形象地讲解电磁场的洛伦兹变换，同时指出了协变性的理解可以使学生更加深刻理解电磁学理论的本质，为后续的量子电动力学做好铺垫。 第二个

例子论文证明了在行列式为1的矩阵变换下n阶反对称张量是不变的。因为洛伦兹矩阵行列式为1，所以四阶反对称张量εμ νρ σ自然是协变的。 由此也可以明白矢量和轴矢量的区别，牛顿力学方程也可以写成手征形式。 这个证明在场论的高级课程中可以方便地解释二阶、三阶以及其他反对称张量的应用。 在第三部分中，论文指出协变性是对物理公式变换性质的表述，而某一个物理量会因为形式不同而有不同协变性的理解。论文以场论散射截面的协变性质为例，指出不同理解的差别与联系。 这一点希望能得到同行的认可。

[1] Goldstein, et al. Classical Mechanics[M]. New York: Pearson Education International. 344.

[2] 张三慧.大学物理学—电磁学[M].3版.北京：清华大学出版社.

[3] 郭硕鸿.电动力学[M].3版.北京：高等教育出版社.

[4] 王青.电磁学与电动力学中的磁单极-Ⅰ[J].物理与工程，2013， 23(6)：8-11； Wang Qing. Magnetic monopole in electromagnetism and electrodynamics-Ⅰ[J]. Physics and Engineering，2013，23(6)：8-11. (in Chinese) 电磁学与电动力学中的磁单极-Ⅱ[J].物理与工程，2014， 24(5)：29-33； Wang Qing. Magnetic monopole in electromagnetism and electrodynamics-Ⅱ[J]. Physics and Engineering，2014，24(5)：29-33. (in Chinese) 电磁学与电动力学中的磁单极-Ⅲ[J].物理与工程，2015， 25(4)：19-24； Wang Qing. Magnetic monopole in electromagnetism and electrodynamics-Ⅲ[J]. Physics and Engineering，2015，25(4)：19-24. (in Chinese) 电磁学与电动力学中的磁单极-Ⅳ[J].物理与工程，2015， 25(5)：33-40. (in Chinese) Wang Qing. Magnetic monopole in electromagnetism and electrodynamics-Ⅳ[J]. Physics and Engineering， 2015，25(5)：33-40.

[5] Peskin M, et al.量子场论导论(影印版)[M]. 新加坡： 世界图书出版社，106.

[6] Thomson M. Modern Particle Physics[M]. Cambridge: Cambridge University Press， 70-72.

■

ON THE TEACHING OF COVARIANCE IN COLLEGE PHYSICS AND FIELD THEORY

Wang Wenyu Wang Siyu Xu Yang

(College of Applied Science, Beijing University of Technology, Beijing 100124)

This paper mainly talked about the importance of covariance in the course of college physics and field theory. We used a figure to show that how to understand the Lorentz Transformation at the end of the course of Electromagnatics. Then we showed that Levi-Civita anti-symmetric tensor is invariant under a transformation matrix which determinant equals one, thusεμ νρ σis a Lorentz covariant tensor, vector and axial-vector have different mirror transformation. At last, we argued that a physical variable will have different properties of covariance under different formulation. As a demonstration, we showed the difference and the relation in the understanding on the cross section in quantum field theory.

covariance； electro-magnetic tensor； levi-civita tensor； cross section

2016-12-01

国家自然科学基金(11375001)和北京市教委青年拔尖项目。

王雯宇，男，副教授，主要从事理论物理的研究和教学工作，主要研究方向为高能物理，超出标准模型新物理，wywang@mail.itp.ac.cn。

王雯宇，王丝雨，许洋. 大学物理和场论课程中的协变性浅谈[J]. 物理与工程，2017，27(1)：30-36.