光源的相干性对牛顿环的影响

吴天一

(镇江船艇学院基础部物理教研室，江苏 镇江 212003)

光源的相干性对牛顿环的影响

吴天一

(镇江船艇学院基础部物理教研室，江苏 镇江 212003)

本文以普通光源和激光为例，探讨了光源的相干性对牛顿环干涉现象的影响。对于非相干光源，研究了单色性对相干长度的影响，指出仅有空气夹层上下表面的反射光会在平凸透镜顶点附近凸面内侧贴近凸面的区域形成一套干涉条纹。对于相干光源，利用斯托克斯定律推导了各表面反射光之间干涉条纹的可见度，进而分析了多套干涉条纹的叠加效果。

相干长度；可见度；干涉

牛顿环于1675年被牛顿首先观察到，这一典型的干涉现象充分体现了光的波动性。对于等厚干涉条纹——明暗相间的同心圆环，物理学教材中都有充分的理论分析，然而对于实验装置中的光源并未特别加以说明，以致在教学中学生会产生这样的疑问：平凸透镜和平板玻璃的上下表面也会产生反射光，为何只考虑空气夹层上下表面反射光的干涉？针对这一问题，本文将以普通光源和激光为例，讨论光源的相干性对牛顿环干涉现象的影响。

1 非相干光照射的情况

大学物理实验中，一般采用普通光源垂直照射牛顿环装置来观察其干涉条纹。普通光源的发光方式是自发辐射，属于非相干光源，需利用振幅分割法把同一光波波列“一分为二”，按理说当这两部分沿着不同路径传播并相遇时，都应产生干涉现象。然而不容忽视的是，每一个波列的长度是有限的，假设自发辐射的弛豫时间是Δτ，则波列的长度为

L=c·Δτ

(1)

这就要求同一波列分成的两部分经不同路径到达相遇点的光程差不能太大，否则波列的一部分已经通过，而另一部分还尚未到达，也就不能产生干涉现象了，因此波列长度也称为相干长度。

对于如图1(a)所示的有限长波列，利用傅里叶变换，可以转化为许多单色波列的叠加，其光强随波长的分布曲线如图1(b)所示[1]，其中最大光强所对应的波长为中心波长λ，光强下降为最大值一半时所对应的波长范围称为谱线宽度Δλ，即普通光源所发出的光是由λ附近许多不同波长的光按一定强度分布组合而成的，Δλ越小表明单色性越好。

图1 普通光源光波(a) 波列示意图； (b) 光强随波长的分布曲线

图2 非单色光源的条纹可见度K随光程差Δ的变化曲线

(2)

(3)

k所对应的最大光程差为

(4)

Δmax即为相干长度。

显然，光源的单色性越好，Δλ越小，Δmax越大，在光程差较大时也能观察到干涉现象，可以获得较高级次的干涉条纹；反之，Δλ越大，Δmax越小，只能在光程差较小时观察到干涉现象，获得低级次的干涉条纹。

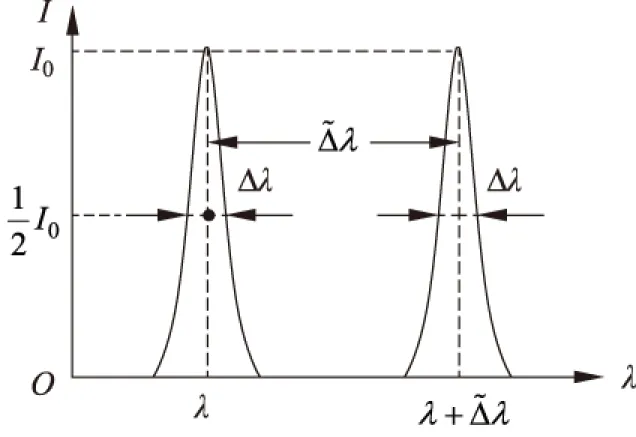
图3 双谱线复合光光强随波长的分布曲线

(5)

(6)

所对应的最大光程差为

(7)

对于由两条波长相近、强度相同的谱线构成的复合光，定义条纹对比度随光程差周期性变化过程中相邻两次条纹消失位置(或相邻两次条纹对比度最大位置)光程差的改变量，为相干长度[4]，则

(8)

2 相干光照射的情况

图4 牛顿环装置

(9)

来描述干涉现象的明显程度。故为使干涉条纹清晰可见，两相干光振幅不能相差太大。

借助斯托克斯定律[1]，可以定量分析各个分界面反射光和折射光的振幅。假设r和t分别代表从空气射向玻璃时反射光和折射光相对于入射光振幅的比值，称为反射比和透射比。若是光从玻璃射向空气，其反射比和透射比分别为r′和t′。由于r′的绝对值等于r，故这里不区分r和r′。若从空气垂直照射在平凸透镜上表面(分界面①)的激光振幅为A0，则反射光振幅为rA0，折射光振幅为tA0；折射光tA0射向平凸透镜的下表面(分界面②)，则反射光振幅为rtA0，折射光振幅为tt′A0；折射光tt′A0穿过空气层射向平板玻璃的上表面(分界面③)，则反射光振幅为rtt′A0，折射光振幅为t2t′A0；折射光t2t′A0射向平板玻璃的下表面(分界面④)，则反射光振幅为rt2t′A0，折射光振幅为t2t′2A0。

对于平凸透镜而言，下表面反射光还需经分界面①折射后才能与上表面的反射光相遇，即平凸透镜上下表面(即分界面①、②)的反射光在相干区域的振幅分别为rA0和rtt′A0，即振幅之比为tt′；对于空气夹层而言，下表面反射光还需经分界面②折射后才能与上表面的反射光相遇，即空气夹层上下表面(即分界面②、③)的反射光在相干区域的振幅分别为rtA0和rt2t′A0，即振幅之比为tt′；对于平板玻璃而言，下表面反射光还需经分界面④折射后才能与上表面的反射光相遇，即平板玻璃上下表面(即分界面③、④)的反射光在相干区域的振幅分别为rtt′A0和rt2t′2A0，即振幅之比为tt′。由此可知，相邻分界面的反射光在相干区域的振幅之比皆为tt′。

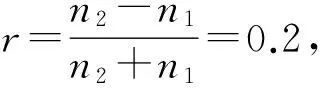
(10)

需要说明的是，平板玻璃厚度处处相等，其上下表面(分界面③、④)的反射光虽然满足干涉条件，但不会形成明暗相间的条纹，其干涉图样亮度处处相等，且亮度取决于平板玻璃的厚度所造成的光程差。也就是说，对于相邻分界面而言，只有平凸透镜和空气夹层上下表面(分界面①、②和②、③)的反射光会形成明暗相间的干涉条纹，且清晰可见。

对于非相邻分界面而言，两反射光在相干区域的振幅之比会有所变化。例如，分界面④的反射光rt2t′A0还需经历2次折射(振幅变为rt(tt′)2A0)才能与分界面②的反射光rtA0相遇，即两反射光在相干区域振幅之比为(tt′)2，干涉条纹的可见度为

(11)

显然，可见度并未出现明显的下降，干涉条纹仍旧清晰可见。需特别说明的是，对于分界面①、③以及①、④，其两分界面上的反射光在相干区域振幅之比分别为(tt′)2和(tt′)3，但考虑到两分界面皆为平面，则若两分界面绝对地平行，即①、③以及①、④之间的厚度处处相等，则两反射光的干涉情况与平板玻璃上下表面反射光的干涉情况类似，不会产生明暗相间的条纹，干涉图样亮度处处相等；若两分界面不绝对地平行，即①、③以及①、④之间的厚度有变化，且变化是线性的，则两反射光相遇后就会出现明暗相间的平行条纹，且干涉条纹可见度分别为0.997和0.993，清晰可见。

因为视场中会出现多套干涉条纹，即对应于不同圆心的明暗相间的圆环，还有可能出现明暗相间的平行条纹，所以从干涉图样的整体呈现效果上看，激光的牛顿环并未比普通光源的牛顿环清晰可见。

3 结语

本文以普通光源和激光为例，从光源相干性的角度讨论了不同光照条件下牛顿环的干涉条纹。用非相干光源即普通钠光源垂直照射时，仅有空气夹层上下表面的反射光会在平凸透镜顶点附近凸面内侧贴近凸面的区域形成一套干涉条纹。用相干光源激光垂直照射时，各个表面的反射光之间均会产生干涉，即会出现多套干涉图样，虽然每套干涉条纹的可见度均很高，但因圆环的圆心不重叠且可能出现平行条纹，故叠加在一起的效果并不及普通光源产生的条纹清晰可辨。

[1] 毋国光，战元龄.光学[M].北京：人民教育出版社，1981：193-216.

[2] 吴健.光学[M].北京：国防工业出版社，2007：103.

[3] 褚圣麟.原子物理学[M].北京：人民教育出版社，1979：115-119.

[4] 康文秀，关荣华.相干长度的物理意义[J].大学物理实验，2005，18(3)：31-32. Cang Wen-xiu, Guan Rong-hua. The physical meaning of coherent length[J]. Physical experiment of college. 2005，18(3): 31-32. (in Chinese)

[5] 袁泉，张玉璞，李义等.Na黄光的相干长度测量与原子发光时间的估计[J].大学物理实验，2015，28(5)：11-13. Yuan Xuan, Zhang Yu-pu. ect. The Experimental Measurement of the Coherent Length for Na Lights and the Estimation of the Light Emitting Time[J]. Physical experiment of college. 2015，28(5): 11-13. (in Chinese)

[6] 姚启钧.光学教程[M].北京：高等教育出版社，1984：34-36.

■

THE INFLUENCES OF LIGHT SOURCE COHERENCE FOR NEWTON’S RINGS

Wu Tianyi

(Basic Department Physics Teaching and Research Section, Zhenjiang Watercraft College， Zhenjiang, Jiangsu 212003)

Taking ordinary light source and laser as examples, the influences of light source coherence on Newton’s rings are discussed in this paper. For the incoherent light source, the effects of monochromaticity on coherence length are studied. It is found that only one set of interference fringes distribute nearby the vertex of the concave mirror, locating inside and next to the concave, which are formed by the air interlayer’s reflected lights. For the coherent light source, the visibilities of the interference fringes formed by any two surfaces’ reflected lights are derived by using the Stokes’ law. Then the overlay of many sets of interference fringes is analyzed.

coherence length; visibility; localization

2016-01-16；

2016-11-07

吴天一，女，讲师，主要从事物理教学科研工作，研究方向为非线性动力学,wutianyiwty@126.com。

吴天一. 光源的相干性对牛顿环的影响[J]. 物理与工程，2017，27(1)：55-58.