基于综合聚类的供电服务满意度测评样本分配研究及应用
樊立攀,叶 利,田晓霞,尚 凡,黄徐珂
(1.国网湖北省电力公司客户服务中心,湖北 武汉 430077;2.国网武汉供电公司,湖北 武汉 430013)
0 引言
近年来,供电服务工作面临着创新服务方式和全面提升服务质量的紧迫要求。开展供电服务满意度测评已成为衡量供电服务质量的重要指标。整个测评过程包含以下4个重要环节:构建指标体系、计算指标权重、分配调研样本、录入数据并计算满意度得分。样本分配方法的选取直接决定了供电服务满意度测评数据的客观性和真实性。在实际测评中,样本分配方案仅从用电水平上区分各地市公司的样本量,造成各个地市样本区分度不高、样本集代表性差的问题。
国内外相关文献中,客户满意度测评样本分配大多采用单一用电特性结合分层抽样为基础的方法[1]。文献[2]提出基于明显用电特征和对用户类型进行分层抽象的方案,该方案在一定程度上优化了样本集,但没有全面考虑影响样本集代表性的因素。文献[3]中使用基于细分业务和抽补的样本分配方案,保证了样本分布与总体分布的近似一致。文献[4]根据服务类别和客户类别2个维度对样本进行分配,但对数据维度充分性以及重要度特征考虑不足。因此需要优化样本集选取,使样本区分度较高,样本集代表性较强。
针对上述问题,本文在充分研究样本分配影响因素的基础上,挖掘具有样本集代表性的属性因素,将其纳入分层抽样的分配原则中,用以提高样本的区分度和代表性。在样本分配中,保证所有地市的样本量满足置信度和抽样误差的要求,对于缺失数据进行插补数据预处理,建立基于综合聚类的样本分配方案,最后通过实例验证了该方案的实效性和可行性。
1 调查样本容量分析
样本量大小的选取直接影响测评的精准度,测评的精准度越高,需要调查的样本数和涉及面就越多,同时工作的难度和复杂度也越高。因此需要在保证抽样调查对估计数据的精确度,尽量减少调查单位数,确保必要的抽样数目。
根据统计学原理:
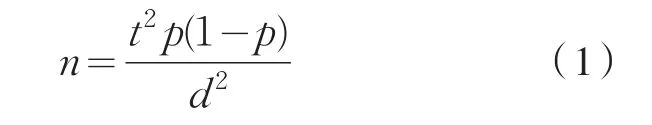
其中:n代表所需要的样本量;
t代表概率度,一般置信度95%时,t=1.96;
p代表总体方差,一般取0.5;
d代表抽样误差。
根据式(1)可知,当选定样本量为16 000时,此时的样本水平满足95%置信度下,抽样误差为0.01%。根据综合测评样本和专项测评样本3:13确定专项样本份数为3 000份,综合样本份数为13 000份。
2 综合聚类分析模型
2.1 K-means聚类原理及其具体思想
K-means聚类原理是数据点到原型的某种距离建立目标函数,利用函数求极值的方法得到迭代运算的调整规则。K-means聚类算法的优点主要集中在:
(1)K-means聚类算法原理简单、易于编程实现;
(2)对大数据集有较高的效率并且是可伸缩性的;
(3)时间复杂度近于线性,而且适合挖掘大规模数据集。
计算各类聚类中心时,采用欧几里德距离。欧几里德距离的远近与相似程度成反比。欧几里德距离的计算公式如式2所示。
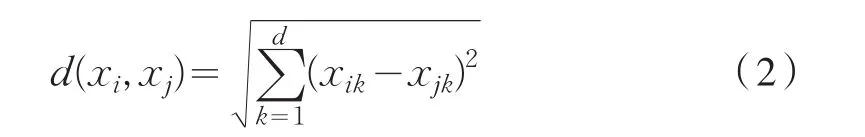
2.2 样本聚类原则
聚类分析需选择合适的聚类原则才进行不同分类。在综合考虑地区经济水平、用电特性和业务量水平3个方面的因素上,选取每类显著性特征因素(人均GDP、客户数和万户业务量)进行分类分析。
(1)人均GDP:根据相关研究,人均GDP与人均用电量呈正相关,用户使用电能和用电场合也会相应增多,与电力部门接触的频率也相对较多。因此对人均GDP较高的地区,也应当投入较多的精力进行供电服务客户满意度调查。
(2)客户数:一般情况下,客户数与售电量成正相关,地区客户数越多,则该地区的总售电量也越多。用电客户和售电量越多,则客户与供电服务接触的频率也越高。
(3)万户业务量:万户业务量越大,则电网和客户接触的接触次数就越多。在办理业务的过程中,客户能直观地对电力部门及电力工作人员的相关工作情况留下一定印象,这一印象则会在某些方面对供电服务满意度评价起决定性作用。
2.3 样本缺失预处理
在测评工作开展的实际过程中,样本数据会产生一定的缺失。针对这种情况,必须采取一定的数据预处理手段,目前常用的数据预处理手段主要采用插补法,插补法包括均值插补、众数插补、中位数插补等。
(1)均值插补:均值插补是指对所有的缺失数据,用所有回答单元观测值的均值进行插补,通过均值插补方法处理数据,能有效地减少缺失数据对最终结果的影响。因此,当样本缺失数过大时,采用均值插补。
(2)众数插补:当非缺失数据为非对称分布,且仅有一个众数时,此时最宜采用众数插补。众数代表了一组数据中出现最多的变量值,其不受极端值影响,能够体现一组数据的主流趋势。在样本信息较大的情况下,众数插补能够最大程度地保持样本的特征及趋势。
(3)中位数插补:当数据信息呈非对称分布,且不存在众数或存在多个众数时,此时宜采用中位数插补的方法。利用中位数插补法能够保证插补值与其他数据的离差最小,从而保证整体数据的整体均衡性。
对于数据信息Xi,通常有以下四种数据分布,如图2-图4所示:

图1 左偏分布 Fig.1 Left-skewed

图2 右偏分布Fig.2 Right-skewed
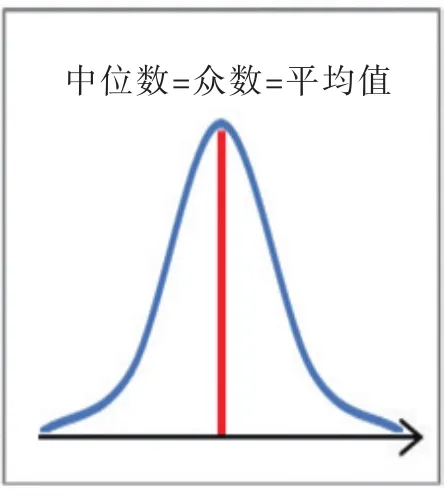
图3 对称分布Fig.3 Symmetrical

图4 众数分布Fig.4 Polymodal
(1)当数据信息如图1所示呈左偏分布时,其众数>中位数>平均值,应采用众数插补;
(2)当数据信息如图2所示呈右偏分布时,其众数<中位数<平均值,应采用众数插补;
(3)当数据信息如图3所示呈对称分布时,其众数=中位数=平均值,应采用均值插补;
(4)当数据信息如图4所示,存在多个众数,应采用中位数插补。
综上所示,样本缺失预处理流程如下:首先判断缺失数据是否超过阀值(本测评数据缺失20%以上,视为超过阈值),若缺失值未超过阀值,则分析非缺失数据的分布,根据不同的数据分布,采用不同的方法对缺失数据进行数值插补。插补模型流程图如图5所示。

图5 插补模型流程图Fig.5 Interpolation flowchart
3 基于综合聚类的样本分配方案
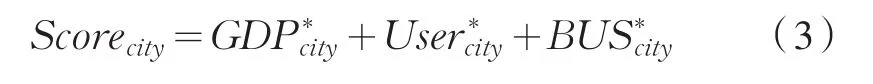
式中,Scorecity——各地市综合指数。
根据式3,可计算出各地市归一化综合指数。将归一化综合指数进行降序排列,由等距选取原则选出第1、5、10、14名地市公司作为初始聚类中心,城市类别的物理含义如下:A、B、C、D类城市分别代表代表人均GDP、客户数、万户业务量的综合水平处于高水平、中高水平、中低水平、低水平。
由于同一类城市的区域经济性、用电特性、业务量水平相近,所以对于同一类城市,采用相同的抽样比。全省平均抽样比为0.74‰。四类城市按照A、B、C、D类顺序,抽样比在全省抽样比的±n%范围内依次递减。n的取值根据实际情况选取,本报告仅例取n=10为例,即A、B、C、D类城市的抽样比在全省抽样比0.74‰*(100%±10%)=0.67‰~0.81‰之间依次递减。在保持每个地市的样本符合抽样误差和置信度的最低要求和分配结果的比例特性的前提下,对结果进行取整微调,使专项综合样本比例大致保持在13:3,最终分配结果如表1。
3.1 各单位样本总体分配
利用K-means动态聚类对上述14个地市进行分类。本方案拟将14个地市供电公司分为A、B、C、D四类等级,引入地市归一化综合指数值的概念量表征各个地市公司的综合水平,该地市的综合指数可由该地市的归一化人均GDP、归一化客户数和归一化万户业务量直接相加得到,即:
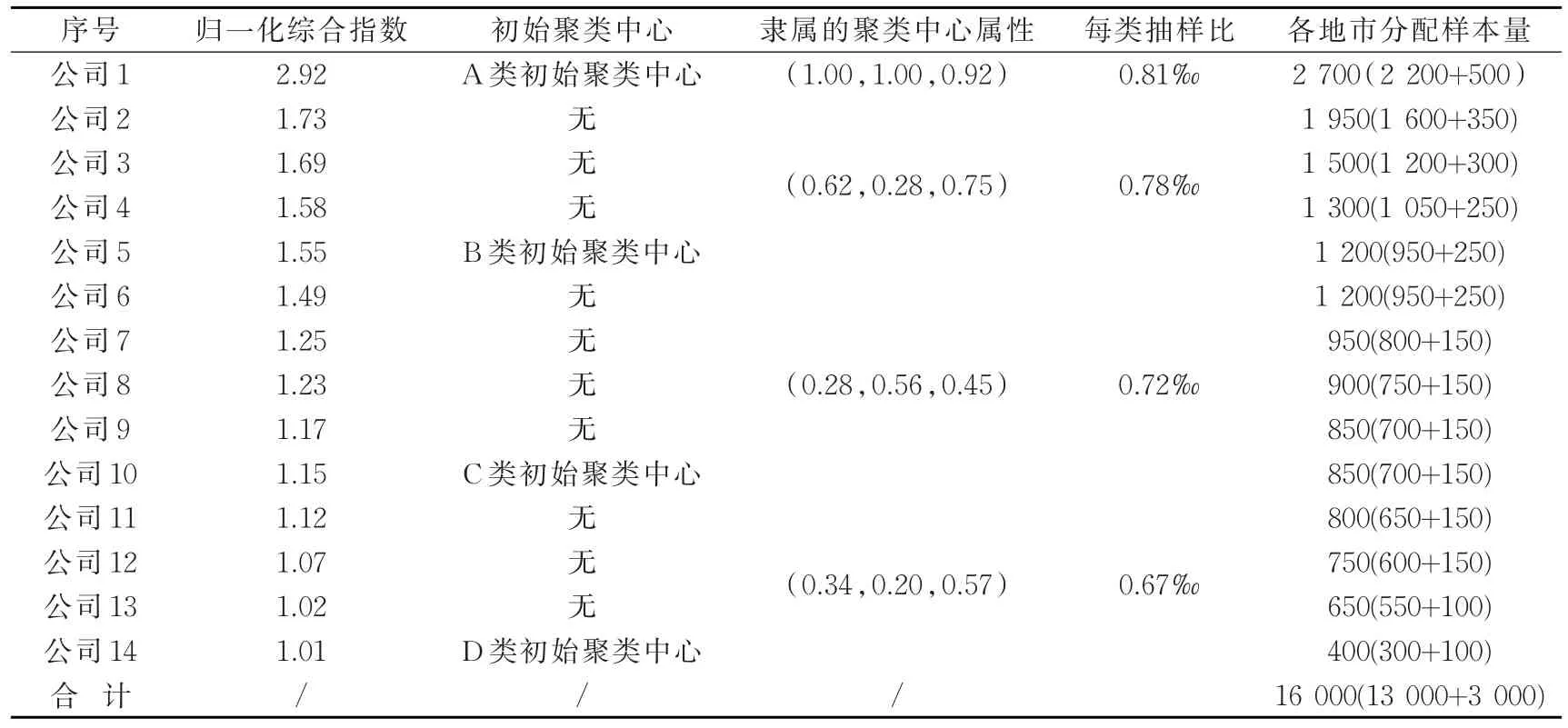
表1 各单位属性信息和样本分配结果Tab.1 Attribute information and sample allocation results
3.2 综合样本各类客户样本分配
各单位客户将分为5个类别进行抽样,分别为大工业客户、一般工商业客户、政府事业单位客户、城镇居民客户、农村居民客户。考虑到大工业客户和政府事业单位客户的数量较少。因此这两类客户根据每个地市的综合样本量采取分级定量分配。
一般工商业客户、城镇居民客户、农村居民客户的样本容量则根据2016年上半年的用电结构数据计算得出。具体计算公式如下:

式中,CoefX_Y——地市供电公司各类客户系数,表示X地市中的Y类客户系数;
UserX_Y——X单位中的Y类客户数;
UserX_Ytotal——X单位3类总客户数;
PowerX_Y——X单位Y类客户近一年售电量;
PowerX_Y total——X单位3类客户近一年的总售电量;
CITYSAMPX_Y——X单位Y类客户样本数;
COMSAMPX——X单位综合样本量;
COMSAMPfixX——X单位定量客户样本量;
K1、K2——待定系数。
其中K1、K2取值如下:
结合实际情况,K1=0.6,K2=0.4,各单位各类客户样本量分配如表2所示。

表2 各供电单位综合样本各类客户分配结果Tab.2 Comprehensive allocation results
3.3 各地市单位专项样本分配
各单位专项指标为业扩报装服务、供电质量服务、抄表交费服务、营业厅服务、信息渠道服务、故障抢修服务和投诉处理服务。在计算过程中,六个专项指标的重要程度由指标权重决定。综合考虑上述原因,2016年各地市各专项指标样本量之比为1,如表3所示。

表3 各地市各专项分配结果Tab.3 Specialized allocation results
3.4 分配数据缺失处理
2015年,满意度测评缺失数据情况如表4所示。
将原处理方法(缺项取‘0’值处理)与均值处理方法的结果作对比,如表5所示。

表4 满意度测评缺失数据汇总Tab.4 Missing data aggregation

表5 原处理方法(缺项取‘0’值处理)与综合插补处理方法的结果对比Tab.5 Comparison between original method and comprehensive interpolation
通过上述分析,即超过90%的地市公司将不会对综合插补处理后的排名产生抱怨。因此说明了对缺失项采用综合插补方法相对原来的采用‘0’值的处理方法要更加合理。
综上,基于综合聚类的满意度测评样本方法分配方案整体流程如图6所示。
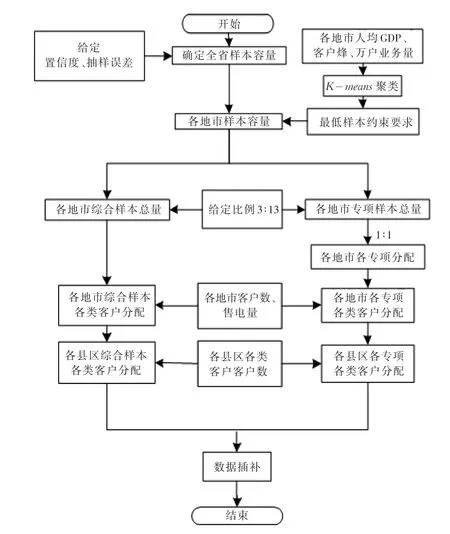
图6 基于综合聚类的样本分配方案流程图Fig.6 Sample allocation flowchart based on comprehensive clustering
4 结语
本文提出了一种综合聚类样本分配方法,通过综合考虑影响样本分配的各项因素,选取强关联性因素聚类分配,使样本分配结果更加突出各个测评单位的差异性,采用多种数据插补处理模型,减少了数据缺失造成的误差。依据此方案进行样本分配,能有效改善样本结构,使样本分配结果更加客观、科学,方便后续样本的分配。
(References)
[1] 王鹤,张婷.基于服务蓝图的电力客户满意度评价研究[J].华北电力大学学报(社会科学版).2007,2(4):7-11.WANG He,ZHANG TingJournal.Research on electric customer satisfactory evaluation based on the service blueprinttheory.JournalofNorth China Electric Power University(Social Sciences),2007,2(4):7-11.
[2] 庄凌晖.如何制定科学合理的供电客户满意度抽样调查方案[J].中国电力教育,2011(15):84-85.ZHUANG LinHui.How to set up a scientific and reasonable sampling survey of Customer satisfaction.China Electric Education,2011(15):84-85.
[3] 罗智超,吴育青.基于电力细分业务抽样调查的客户满意度模型[J]广东电力,2010,23(11):64-66.LUO Zhichao,WU Yuqing.Customersatisfaction model based on sub electric business sampling[J].Guangdong Electric Power 2010,23(11):64-66.
[4] 张立娟,张克众.提高基层供电服务满意度策略分析[J].电力需求侧管理,2015,17(1):49-51.ZHANG Lijuan,ZHANG Kezhong.Strategy analysis of improving service satisfaction of basic level power supply[J].Power DSM 2015,17(1):49-51.
[5] 王平,邹珊刚.电力行业用户满意度指数模型构建与实证研究[J].武汉理工大学学报(信息与管理工程版),2006,28(3):145-149.Wang Ping,Zou Shangang.Construction and empirical Analysis of the customers satisfaction index of chi⁃nese electricity industry[J].Journal of WUT(Informa⁃tion&Management Engineering)2006,28(3):145-149.
[6] 霍映宝,徐莉,吴国英.供电行业用户满意度模型构建及实证研究[J].管理学报,2009,12(6):1696-1701.HUO Yingbao,XU Li,WU Guoying.Construction and empirical analysis of the customer satisfaction model for power supply industry[J].Chinese Journal of Management,2009,6(12):1696-1701.
[7] 霍映宝.供电服务质量与客户满意关系的实证研究[J].统计与信息论坛,2008,5(10):39-43.HUO Yingbao.An empirical research on the rela⁃tionship between power supply service quality and customer satisfaction[J].Statistics&Information Fo⁃rum,2008,5(10):39-43.

