Rayleigh-Benard对流中的分歧解

周 洋，李 玫，周 强

(1.成都大学建筑与土木工程学院，成都 610106；2.成都大学信息科学与工程学院，成都 610106)

Rayleigh-Benard对流是研究非线性动力学特性的典型模型之一。在日常生活中这种对流现象较为多见，例如水库分层和湖泊分层现象，这些现象可帮助人们对对流现象的理解。Rayleigh-Benard对流是指在一个封闭的渠槽内，下表面均匀或者周期性加热，上表面温度保持一定，上下表面形成的温度差超过某个临界数值时，就会导致渠槽内流体流动的现象。对于这种流动，Rayleigh与Benard先后进行了理论与试验分析，从而被称作Rayleigh-Benard对流[1-3]。

Rayleigh-Benard对流是传热学中典型的热对流问题，简称RB对流。RB对流可以产生非常有趣的流场时空结构。许多科研工作者在混合流体方面的研究比较深入，并取得了大量而有意义的成果。而对纯流体对流研究尚不多见。本文以纯流体的Rayleigh-Benard对流为例，经过模拟发现了定常流动解的不唯一性。存在着分歧解。

1 数学模型

1.1 流体力学基本方程组[4]

以一个封闭的渠槽作为研究对象，如果上部平板的温度固定不变，保持常数。当下部平板的温度升高到某个数值时，由于上下表面流体密度的不同，导致了在两平板之间将会发生流体对流现象，对流运动的流场时空结构随上下板之间温度差的变化而变化。假设坐标原点位于底板与左侧壁的交汇处，x轴向右为正，z轴向上为正。流卷的轴线保持平行，在布西涅斯克假设下，流体力学方程组如下：

▽U=0

(3)

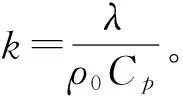
假设温度场 距离平均值波动很小，质量密度的状态方程可表示为：

ρ=ρ0[1-α(T-T0)]

(4)

式中由加热引起的体积膨胀系数可表示为：

(5)

如果把流体层厚度d作为长度的量纲，那么时间可表示为d2/k，速度可表示为k/d，压强可表示为ρ0k2/d2，流体力学基本方程组无因次化可表示为：

▽·δU=0

(6)

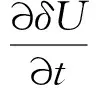
(7)

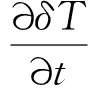
(8)

式中：R为瑞利数；Pr为普朗特数；δT=(T-T0)/ΔT，ΔT为上下壁面的温差。

1.2 计算的初始条件和边界条件

为了准确求解方程组必须给出合理的边界条件。研究区壁面为固体壁面，壁面上速度为0。初始条件，δu=δw=0，初始温度取上下壁面温度的平均值。具体边界条件为，当z=0，1时，δu=δw=0；当x=0，Γ时，δu=δw=0。

δu为水平流速，δw为垂向流速。

1.3 数值计算方法

本次对流体力学方程组的求解使用流体力学计算软件FLUENT，计算采用双精度有限差分法，计算区域的长高比 =10，计算区域中采用均匀网格。时间步长取0.01 s。

下面讨论Pr=1和Pr=6.99两种情况下的定常流动情况下的数值模拟结果。

2 模拟结果与结论

2.1 Pr=1情况下定常流动的对流结构

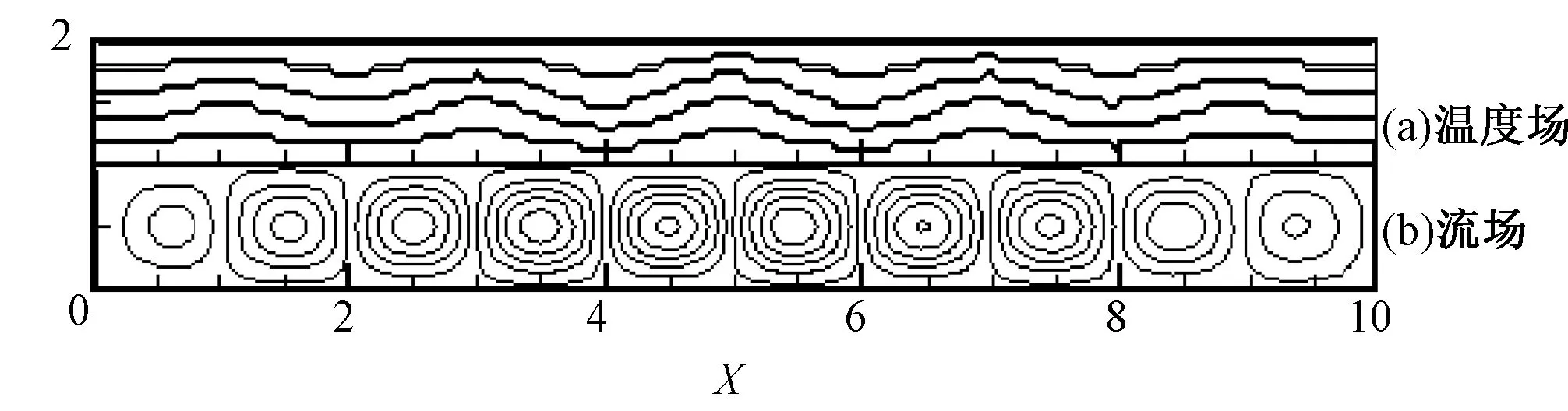
图1 R=1 878.8 对流场空间分布结构Fig.1 The space distribution structure of convection field for R=1 878.8

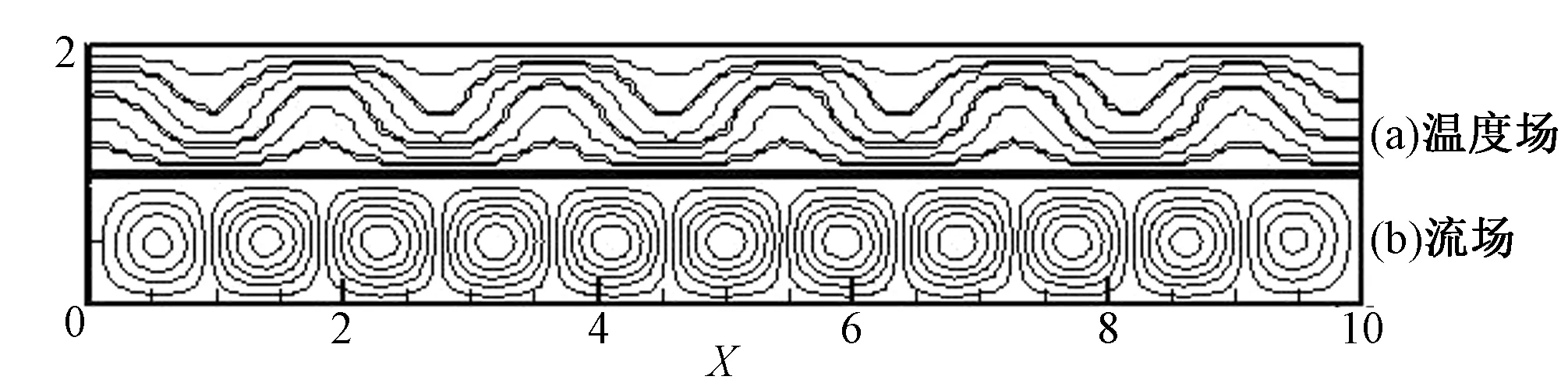
图2 R=2 930.6对流场空间分布结构Fig.2 The space distribution structure of convection field for R=2 930.6

初始条件无论怎么变化，就会只有这两种情况。经过计算模拟，当R=1 878.8～2 732.8，对流只会出现一种波数的情况，即出现10个对流滚动圈，当R=2 930.6～3 416，流场会出现11个对流滚动圈。参考文献5也得出，相对瑞利数在1.1～25，即R=1 878.8～42 700之间，流体的对流滚动圈存在着多种稳定的状态。这说明对流的解存在了分歧[6-9]，验证了本文计算结果的正确性。

2.2 Pr=6.99情况下定常流动的对流结构

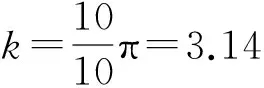
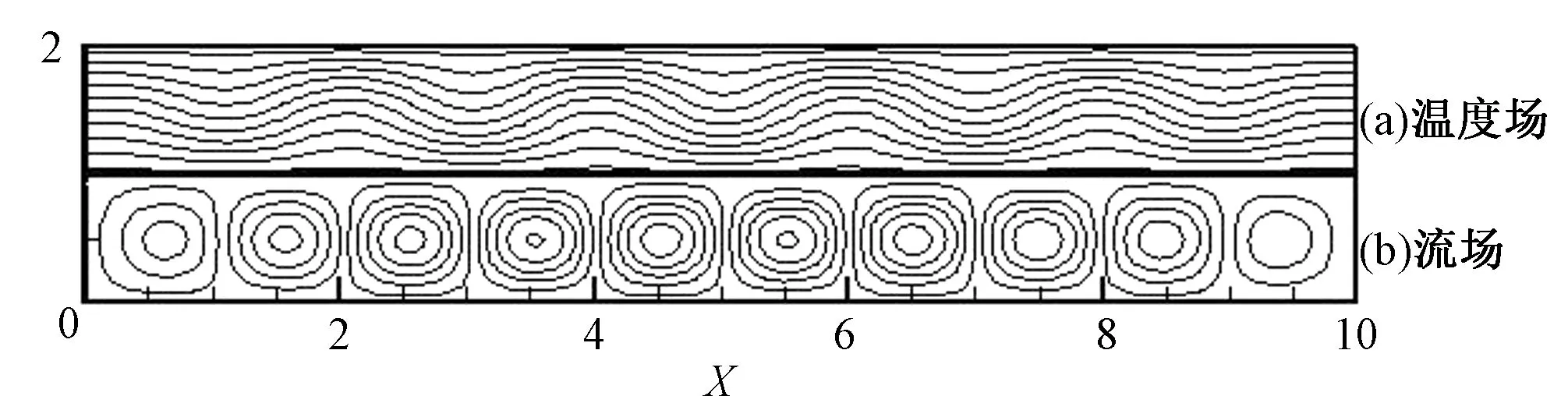
图3 R=1 878.8对流场空间分布结构Fig.3 The space distribution structure of convection field for R=1878.8

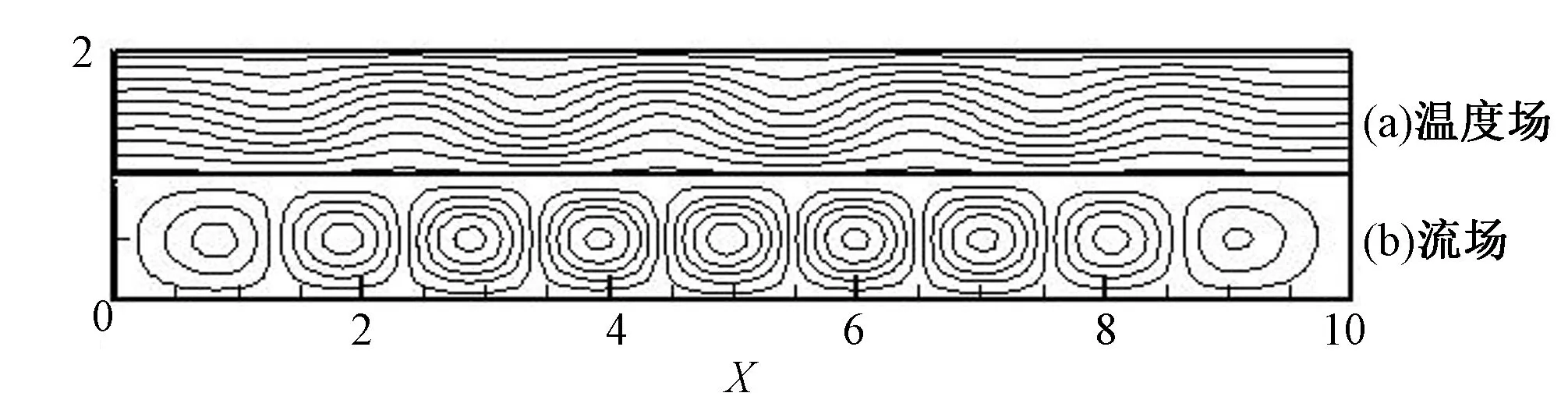
图4 R=1 878.8 对流场空间分布结构Fig.4 The space distribution structure of convection field for R=1 878.8

同样经过长时间稳定计算，当R=1 878.8～2 903.6，对流滚动一直维持着两种波数的情况。当R=3 074.4～3 416，对流将不在维持两种波数的对流滚动圈了，会出现3种波数的对流圈。给定初始条件出现了9，10，11个3种 对流滚动圈。这也说明了解的不唯一性和不稳定性。参考文献[5]也得出，相对瑞利数在1.1～25之间，即R=1878.8～42700之间，流体的对流滚动圈存在着多种稳定的状态。验证了本文计算结果的正确性。图5是11个滚动圈的对流结构。

图5 R=3 074.4对流场空间分布结构Fig.5 The space distribution structure of convection field for R=3 074.4

3 结 语

本文通过对二维流体力学基本方程组的数值模拟,讨论了Pr=1和Pr=6.99两种流体的对流流场结构。当Pr=1时，R在某个范围内R=1 878.8～2 732.8，对流的解是唯一的，超过这个范围，R=2 930.6～3 416，就会出现分歧现象。解是不唯一的。当Pr=6.99时，在某个范围内R=1 878.8～2 903.6出现了两种波数的对流滚动圈，当R=2 930.6～3 416，这种情况将会出现3种波数的对流滚动圈。

□

[1] Cross M C，Hohenberg P C. Pattern formation outside of equilibrium [J]．Review of Modern Physics, 1993,65(3):998-1 011．

[2] Getling A V. Rayleigh-Benard convection[M]．London: World Scientific，1998．

[3] Chandrasekhar S．Hydrodynamics and hydromagnetic stability[M]． Oxford: Clarendon Press，1961：22-26.

[4] 梅 欢.谱元方法求解不可压缩流体流动及流动线性稳定性分析[D]. 重庆：重庆大学，2012.

[5] 周 洋.具有水平流动的Rayleigh-Benard对流[D].西安：西安理工大学，2009.

[6] Ning Lizhong，Harada Y, Yahata H. Transition of convection patterns in a rectangular cell [J]. Journal of Hydrodynamics,2001,13(4):65-71．

[7] 杨 茉,崔晓钰,陶文铨, 等.低Prandtl数水平流体层自然对流的振荡和分歧[J]．工程热物理学报，2000，21(4)：461-465．

[8] Ning Lizhong, Harada Y, Yahata H, et al. Fully developed traveling-wave convection in binary fluid mixtures with lateral flows[J]．Progress of Theoretical Physics, 2001,106(3):503-512．

[9] Ning Lizhong, Haradan Y, Yahata H. Modulated Traveling waves in binary fluid convection in an intermediate-aspect-ratio rectangular [J]．Progress of Theoretical Physics,1997,97(6):831-848．