基于SCE-UA算法的新安江模型与垂向混合产流模型参数优化应用研究

王 维，冯忠伦，杨 伟，林洪孝，王 刚，刁艳芳

(山东农业大学水利土木工程学院，山东 泰安 271018)

0 引 言

洪水是自然界对人类的主要威胁之一。洪水预报就是在流域上发生的暴雨及河流上游的水流补给，经过水情信息采集、传输、存贮、处理等一系列的科学计算，最终预估在流域出口断面或河流下游水文站即将发生的实际洪水过程。做好洪水预报，关键是选择适应流域情况的水文模型以及确保模拟结果精度。前者主要表现在产汇流结构，后者则主要反映在所采用的参数组上[1]。

模型参数的确定方法总体可分为人工试错率定和自动优化率定两种。人工率定得来的参数经验性较强，具有极大的主观性且极为耗时。故在生产实践中人们开始寻求参数求解的程序化实现。而针对参数的不确定性，理解也从最初的局部寻优过渡到寻找全局最优解[2]，此过程涌现了诸如遗传算法、粒子群优化算法、SCE-UA等优秀算法。其中SCE-UA算法是一种结合了基因算法、单纯形算法优点，以信息共享和生物演化规律为基础的非线性混合算法。能在不需要显式目标函数或目标函数的偏导数情况下有效解决高维参数全局优化问题，在应用过程中被证明更适应各类水文模型求参[3,4]。

本文针对山东境内一般山丘地形的田庄水库流域，选取了三水源新安江与垂向混合产流两种模型结构，将SCE-UA优化后的参数带入，对典型洪水进行模拟与检验。

1 SCE-UA算法

SCE-UA(Shuffled Complex Evolution Algorithm)是美国亚利桑那大学的Duan博士等人在原有单纯性算法基础上结合生物与基因选择原理后研究出的一种能够有效解决非线性约束最优化问题的算法，为高效筛选多参数组合的全局最优解提供了一种新的思路。其算法流程见图1。算法中：n为所选参数组参数个数，m代表所选每个复合形顶点个数，p为复合形个数，q为每个子复合形顶点数，s代表种群大小，α、β是父代产生的子代个数及代数。SCE-UA方法的主要步骤为[5,6]：

图1 SCE-UA算法流程图Fig.1 Flowchartof the SCE-UA algorithm

(1)初始化，选取参与进化的复合形个数p(p≥1)，每个复合形包含定点数m(m≥n+1)与样本数s；

(2)产生样本，在可行空间随机产生s个点x1,x2,…,xs并计算每个点xi处函数值fi=f(xi),=1,2,…,x；

(3)样本点排序，将s个点以升序排列，并将它们贮存到数组中D={xi,fi,i=1,…,s}此时i=1代表了目标最小的函数点；

(4)复合形群体划分，将D划分p个复合形分别为A1,…,Ap，每个复合形包含m个点，组成数组A，使：Ak={xk,j,fk,j|xk,j=xk+p,j-1,fk,j=fk+p,j-1,j=1,2,…,m}；

(5)复合群体进化，根据竞争复合形演化算法对每一个复合形(Ak,k=1,2,…,p)进行演化；

(6)混合复合形，将A1,…,Ap代替到D中，有新的D={Ak,k=1,…,p}，再次对D按目标函数的升序进行排列；

(7)收敛性判断，如果满足收敛条件则停止，否则返回步骤(4)。

2 所选模型结构与参数

2.1 三水源新安江模型

新安江模型是以蓄满产流为主的水文预报模型[7]。在湿润与半湿润地区有较为广泛的应用[8]。本文所选新安江模型，产流部分用蓄满产流计算径流量，蒸散发部分按上层、下层和深层三层计算，水源部分采用自由水蓄水库划分为地表、壤中和地下径流3种，地面汇流采用单位线法，壤中流与地下径流用线性水库计算，河网汇流采用滞后演算法。因所选田庄水库流域，以水库以上面积为一个完整单元进行模拟预报，前期对流域洪水由距法分析推得瞬时单位线参数n=1.90，k=4.41。

2.2 垂向混合产流模型

混合产流模型是为解决蓄满与超渗均无法忽略地区产流问题而提出的。混合产流至今还没有形成一套独立的产流理论[9]，其研究通常以蓄满产流和超渗产流两种典型理论为基础。目前常用的混合产流计算方法是垂向混合结构法[10]。此方法是把流域产流过程中地面径流部分按超渗产流，地面以下按蓄满产流进行计算，具体结构见图2。

图2 垂向结合法结构图Fig.2 Vertical binding assay structure

按此方法计算的流域蓄满与超渗面积比例反应在前期土壤含水量与实际下渗量随时间的变化上，可用下式表示：

(1)

式中：γ为蓄满产流的面积比例系数；FA为实际下渗量；Wmm代表流域最大蓄水量；B代表流域蓄水容量分布曲线指数；a相应于初始土壤平均含水量为W时的纵坐标值。

超渗产流计算部分即地面径流RS，用格林-安普特下渗曲线[11]进行计算，计算公式为：

(3)

RS=PE-FA

(4)

式中：FM为流域平均下渗能力；FC为稳定下渗率；WM为流域平均蓄水容量；W为流域实际土壤含水量；KF为土壤对下渗率影响系数；BF为下渗率分布曲线指数；PE为扣除雨间蒸发的降雨量。

蓄满产流计算部分即地面以下的径流(壤中流与地下径流之和)RR，计算公式为：

(6)

综上所述，产流量R=RS+RR，其余部分与新安江模型描述相同。

3 优化过程

3.1 确定模型参数边界

参数边界由模型应用情况人为给定，三水源新安江模型应用较多，参数范围参照参数物理意义及此方面已有研究成果[8,12]给出；对于垂向混合产流模型研究成果有限，参照瞿思敏教授在沐河上游青峰岭水库研究结果[10]，对参数范围进行调整。模型参数边界选择见表1。

表1 模型参数范围Tab.1 The range of mode parameters

3.2 选取SCE-UA算法参数

算法内部参数取值，一般取m=2n+1，q=n+1，α=1，β=m，模拟效果较好[13]。p的取值反映收敛的快慢及收敛精度。过小会降低参数模拟精度，过大则会延误收敛速度，应视具体问题进行分析。一般地，p值越大，越适宜于高阶非线性问题，本文所选三水源新安江模型变化参数n1=13，垂向混合产流模型n2=16，所选流域统一取p=8[14]。

3.3 建立目标函数

目标函数的选取对优化的最终结果有很大影响，针对田庄水库流域洪水实际情况，在考虑洪量与洪水过程后，将洪峰峰值作为一个单独的指标纳入目标函数。对洪水模拟，选取以下3个方程之和作为最终目标函数FObj。有：

(10)

式中：QS来表示实测洪水数值；Qj表示模拟洪水数值。方程fObj1用来控制洪量，保证水量平衡；fObj2反应洪水过程，用来保证单位时段内模拟流量与实测流量变化趋于一致；fObj3用来控制模拟洪峰与实测洪峰误差。

3.4 设定迭代终止条件

为防止参数寻优过程中出现死循环，为程序运行过程设置终止条件，设计满足以下两个条件中任意一个，程序停止迭代，输出参数组最优解：①目标函数在5次循环后仍无法提高0.01%的精度情况下；②5次循环后算法仍无法显著改变参数值并且无法改善目标函数。

4 案例分析

田庄水库地处沂河上游，属暖温带半湿润季风气候，集水面积417 km2。流域均为山区，多年平均降水量850 mm，多年平均径流深320 mm。模型输入部分从流域内双庙、徐家庄等8个雨量站收集点雨资料转换为面雨量，蒸发资料移用流域上游镇后水文站；流量资料选择田庄水库流域内配套参证水文站朱家庄的数据与模拟结果比较。

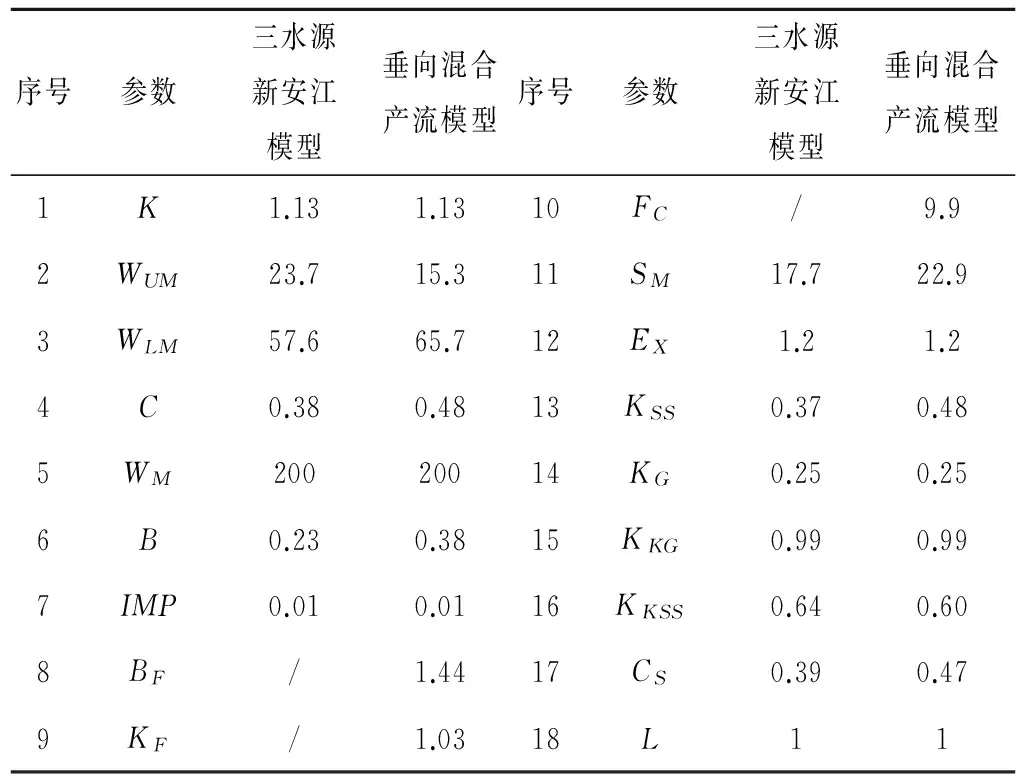
表2 模型参数优化结果Tab.2 Results of parameter optimization

模型参数按3.1节所给边界范围内随机产生后纳入流程循环体中优选，选取田庄水库流域1985～2011年共27 a的18场典型洪水进行模拟，其中前12场洪水用于参数率定，后6场洪水用于参数检验。参数优化结果见表2。可以看出，优化后同一参数在两种模型内取值略有不同，主要体现在垂向混合产流模型的蓄水容量面积曲线指数B与深层蒸散发系数C比三水源新安江模型偏大，这是由于产流部分不尽相同，参数取值基本能反应所代表的物理实质。洪水模拟成果见表3，其中率定期与验证期各选两场，典型洪水模拟过程见图3。

从洪峰洪量角度，由表3可以看出：两种模型模拟的洪峰，洪量误差大都能够控制在容许范围内。从误差的区间分布上来看，正负分布相对平衡，说明模拟的系统误差较小。按洪峰洪量不超过实测20%来评判，模拟的18场洪水中，三水源新安江模型洪量相对误差有3场不合格，全部集中在率定期，洪量合格率83.3%，洪峰相对误差在率定期有1场不合格，洪峰合格率94.4%；垂向混合产流模型洪量相对误差率定期2场、验证期1场，洪量合格率83.3%，洪峰相对误差验证期有1场不合格，洪峰合格率94.4%。

从确定性系数角度，由表3可以看出：SCE-UA优化后三水源新安江模型拟合洪水中确定性系数大于0.9的有3场，0.8～0.9之间的有5场，0.7～0.8之间的有5场，0.7以下的有5场；SCE-UA优化后三水源新安江模型拟合洪水中确定性系数大于0.9的有2场，0.8～0.9之间的有9场，0.7～0.8之间的有4场，0.7以下的有3场。可见，优化后的垂向混合产流模型模拟的洪水过程更符合实际。

图3 典型洪水模拟过程线Fig.3 Simulation hydrograph for typical flood

5 结 论

本文将SCE-UA算法应用到新安江模型和垂向混合产流模型参数优化过程中，从田庄流域的模拟可以看出：①SCE-UA算法适于两种模型的参数优化，并能取得较好的模拟效果；②对于田庄水库流域，优化后的垂向混合产流模型模拟结果要略优于三水源新安江模型；③SCE-UA优化后的垂向混合产流模型比三水源新安江模型更适合模拟相关流域的洪水过程；④确定性系数不是很高，考虑可能因为所选较流域处于北方半湿润地区，流域面积小，洪水涨落迅速且流域洪水成因复杂；⑤两种模拟洪水过程线退水段与实际有一定的差别，地下产流及汇流结构有改善的空间。

□

[1] 孔凡哲，宋晓猛，占车生，等. 水文模型参数敏感性快速定量评估的RSMSobol方法[J]. 地理学报，2011，66(9):1 270-1 280.

[2] 郭 俊，周建中，周 超，等. 概念性流域水文模型参数多目标优化率定[J]. 水科学进展，2012，23(4):447-456.

[3] 宋星原，舒全英，王海波，等. SCE-UA、遗传算法和单纯形优化算法的应用[J]. 武汉大学学报(工学版)，2009，42(1):6-9，15.

[4] Kuczera G. Efficient subspace probabilistic parameter optimization for catchment models[J]． Water Resources Research， 1997，33(1): 177-185．

[5] Sorooshian S， Duan Q Y， Gupta V K. Optimal use of the SCE-UA global optimization method for calibrating watershed models[J]. Journal of Hydrology， 1994，158(3-4):265-284.

[6] Eckhardt K， Arnold J G. Automatic calibration of a distributed catchment model [J]. Journal of Hydrology，2001，251(1-2):103-109.

[7] 董洁平，李致家，戴健男. 基于SCE-UA算法的新安江模型参数优化及应用[J]. 河海大学学报(自然科学版)，2012，40(5):485-490.

[8] 赵人俊. 流域水文模拟—新安江模型与陕北模型[M]. 北京:水利电力出版社，1984.

[9] 包为民，王从良. 垂向混合产流模型及应用[J]. 水文，1997，(3):19-22.

[10] 瞿思敏，包为民，张 明，等. 新安江模型与垂向混合产流模型的比较[J]. 河海大学学报(自然科学版)，2003，31(4):374-377.

[11] 包为民. 格林—安普特下渗曲线的改进和应用[J]. 人民黄河，1993，(9):1-3.

[12] 舒 畅，刘苏峡，莫兴国，等. 新安江模型参数的不确定性分析[J]. 地理研究，2008，27(2):343-352.

[13] Duan Q Y， Gupta V K， S Sorooshian. Shuffled complex evolution approach for effective and efficient global minimization[J]. Journal of Optimization Theory and Applications， 1993， 76(3): 501-521.

[14] 李向阳，程春田，武新宇，等. 水文模型模糊多目标SCE-UA参数优选方法研究[J]. 中国工程科学，2007，9(3):52-57.