改进GA-BP模型在地下水位埋深预测中的应用

杜云皓，仇锦先，冯绍元

(扬州大学水利与能源动力工程学院，江苏 扬州 225009)

0 引 言

河套灌区位于内蒙古巴彦淖尔市，是我国的大型引黄灌区。近年来随着引黄水量的减少与未来40 亿m3/a总量控制，灌区发展节水灌溉(包括井灌)的规模逐年加大，历年地下水位总体呈下降趋势。若地下水位埋深过低，破坏了地下水动态平衡，也降低了地下水对作物耗水的贡献度，甚至引起荒漠化等生态问题。因此，开展灌区地下水位埋深预测与变化规律研究[1]，有效控制地下水位，对地下水资源开发利用、节水措施选择及其实施规模等方面均有重要的指导意义。

关于地下水位埋深预测，目前已有学者提出了多种方法。其中，解析法[2]、数值模拟[2]、小波分析法[3]和时间序列法[4]等方法预测地下水位，存在预测精度低、问题简单化、操作复杂等不足[5]；移动平均法预测地下水位，因问题简单化而无法做长期预测[6]；灰色模型用于地下水位预测，也存在水位变幅大、预测精度低的问题[7]。随着近年来智能算法的不断发展，BP神经网络(Back Propagation Neural Network)在地下水位预测中应用广泛[8]。BP神经网络是一种按误差逆传播算法训练的多层前馈型网络，能够很好处理复杂非线性函数关系，其特点是信号前向传递，误差反向传递[9]。一个典型的BP神经网络是由一个输入层(input layer)、n个隐层(hidden layer)、一个输入层(output layer)构成[10]，如图1所示。

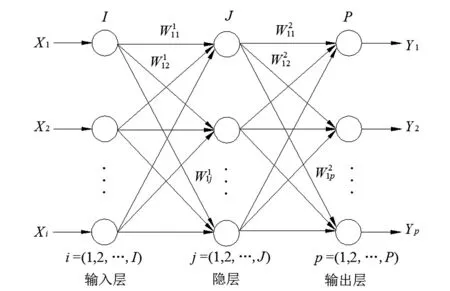
图1 BP神经网络结构图

BP网络理论上能够逼近任何输入变量和输出变量之间的非线性关系，而无需构建非线性模型函数表达式。同时，BP神经网络本身也有其局限性，主要包括以下几点[11,12]：梯度下降法在不同的起点会产生不同的局部最小值，导致BP神经网络最后收敛得到的解不一定是全局最优解；收敛速度慢；网络结构难以确定。

遗传算法GA(Genetic Algorithm)是一种模拟自然界进化规律的一种随机搜索方法，具有较强的全局寻优能力，通过选择适应度函数，选择、交叉、变异对个体进行筛选，保留适应度更好的个体，淘汰适应度差的个体，从而得到基于上一代的新群体[13]。但是遗传算法本身还存在容易早熟、全局收敛性低、运算时间长等问题[14]。本文在遗传算法优化BP神经网络的基础上，改进遗传算法交叉、变异设计，对河套灌区解放闸灌域地下水位埋深进行预测，所得结果与BP神经网络、传统遗传算法优化BP神经网络相比，具有较快的收敛速度和较高的预测精度。

1 改进遗传算法的BP神经网络设计

本文神经网络设计主要包括BP神经网络的建立、权值与阈值遗传算法优化、BP神经网络预测结果输出。本文以Matlab软件为平台，在建立BP神经网络的基础上，首先通过遗传算法选择、交叉、变异操作和适应度计算，得到网络最优权值、阈值，然后开始训练网络、仿真测试，最后预测结果输出[15]。算法流程见图2。

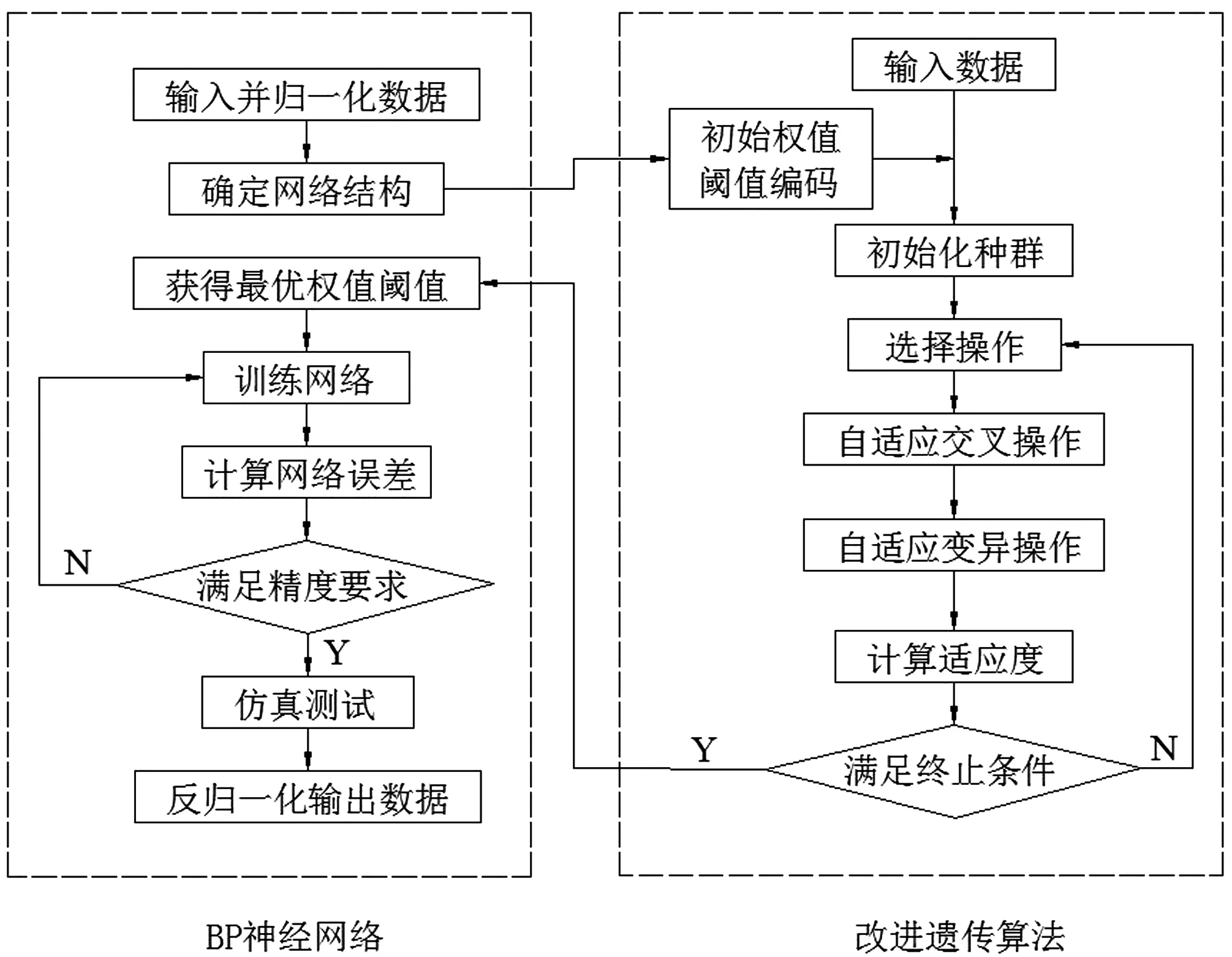
图2 改进遗传算法优化BP神经网络流程图

1.1 编码和适应度函数设计

传统遗传算法采用二进制编码，编码串长，在运算的过程中需要不断地编码和解码，影响神经网络的学习和训练效率，并且在编码长度的选择上没有一定规律[16]。因此，本文个体编码采用实数编码。

在适应度函数设计中，使用初始创建BP神经网络训练得到的预测值与实测值的误差平方和作为适应度值F，公式[17]如下：

(1)

式中：yi为实测值；gi为网络预测值；n为输出节点数；k为系数。

1.2 选择操作设计

选择操作是遗传算法中对个体适应能力的挑选过程，适应能力越大的个体被选择的概率越大，同时决定了一个种群收敛速度。遗传算法的选择操作有轮盘赌法、截断选择法和锦标赛法等[18]。本文采用容易实现、应用较广的轮盘赌选择法，即每个个体选择概率pi为：

(2)

式中：fi为个体的适应度值倒数；n为个体数。

1.3 交叉操作改进

本文遗传算法中的交叉操作，采用单点交叉。单点交叉简单方便，不会对个体造成破坏；交叉概率选择自适应交叉概率。交叉概率过大，适应度大的个体可能遭到破坏；交叉概率过低，会影响遗传算法进化速度[19]。本文对自适应交叉概率[20]进行了改进，算法公式如下：

(3)

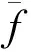
在实数编码设计下，交叉操作采用实数交叉操作，选取两父辈的交叉点y1(i,j)和y1(k,j)，公式[21,22]如下：

y2(i,j)=u1y1(k,j)+(1-u1)y1(i,j)

y2(k,j)=u1y1(i,j)+(1-u1)y1(k,j)

(4)

式中：y1(i,j)为第i父辈的第j位交叉点；y1(k,j)为第k父辈的第j位交叉点；y2(i,j)、y2(k,j)为交叉操作产生的子辈；u1为(0,1]中的随机数。

1.4 变异操作改进

本文遗传算法中的变异操作，选择自适应变异概率。变异概率过大，可能会破坏适应度大的优秀个体；变异概率过低，会影响遗传算法对神经网络的优化能力。因此需要针对不同适应度的个体，选择不同的变异概率。本文对自适应变异概率[20]进行了改进，算法公式如下：

(5)

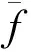
变异操作选取第i个体的第j变异点g1(i,j)进行变异，公式[21,22]如下：

(6)

式中：T=(1-n/m)u3，其中n为遗传算法当前迭代次数，m为总迭代次数，u3为随机数；gmax为g1(i,j)的上界；gmin为g1(i,j)的下界；u2为(0,1]中的随机数。

1.5 BP神经网络设计

本文BP神经网络隐层神经元传递函数采用双曲正切函数tansig，输出层神经元传递函数采用线性函数purelin；输入层节点数为6，隐层节点数为6，输出层节点数为1；误差精度设为0.000 1，学习速率设为0.1；采用三隐层的神经网络设计。

2 应用实例

2.1 基本资料

解放闸灌域为河套灌区五大灌域之一，地处干旱、半干旱地区，夏季高温干燥、降水少、蒸发大，冬季寒冷冻土时期长。农田灌溉水源主要来自于黄河引水，地下水资源主要来自于引黄灌溉水的下渗补给。搜集与整理解放闸灌域2000-2013年逐月地下水位埋深、降水量、引水量、排水量、蒸发量、地下水开采量等基本资料。

2.2 输入输出因子选择

分析各种输入因子与输出因子的相关性，合理选择输入因子的类型与个数，是保证BP神经网络预测精度的前提。解放闸灌域有较完善的灌排系统，地下水位埋深主要受引水量、排水量和气象条件等因素影响[12]。本文以上月地下水位埋深、本月引水量、降水量、蒸发量、排水量、地下水开采量为输入变量，以本月地下水位埋深为输出变量。

2.3 模拟分析

这里选取解放闸灌域2000-2012年逐月地下水位埋深、引水量、降水量等资料，首先分别采用BP模型、传统GA-BP模型、改进GA-BP模型训练网络，然后再分别对该灌域2013年12个月的地下水位埋深进行预测。3种模型预测结果如表1和图3所示。在多次神经网络模拟测试中，遗传算法优化的BP神经网络预测要比传统BP神经网络更加稳定、精度更高；改进遗传算法优化的BP神经网络在预测精度和运算速度上都优于传统遗传算法优化的BP神经网络。

这里采用纳什效率系数NSE(Nash-Sutcliffe efficiency)来反应神经网络预测精度，公式如下：

(7)

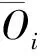
经计算，BP模型NSE为0.743，传统GA-BP模型NSE为0.842，改进GA-BP模型NSE为0.886。

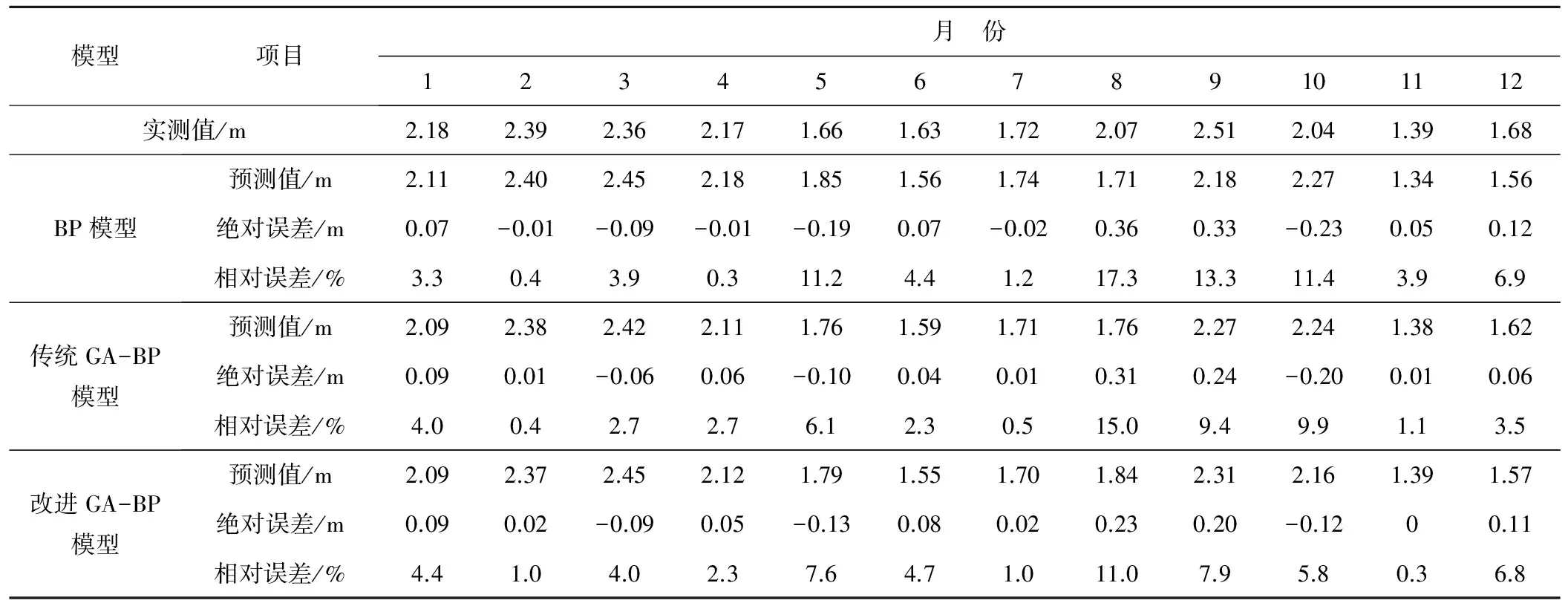
表1 3种模型预测地下水位埋深结果表

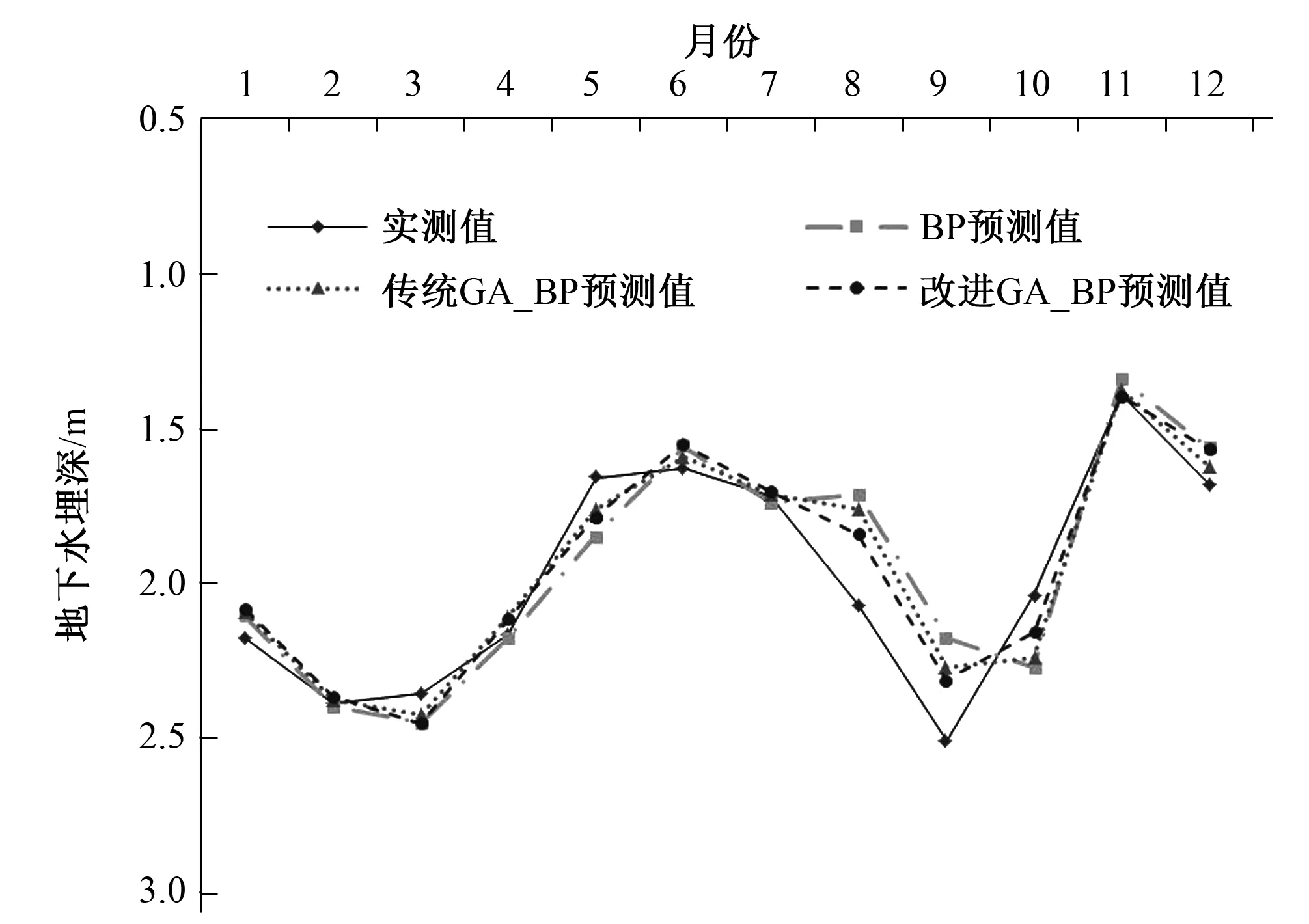
图3 地下水位埋深3种模型预测值与实测值逐月分布图

3 结 语

(1)本文采用Matlab软件实现了BP神经网络编程。结果表明，Matlab提供了大量的数学运算函数，可以快速构建神经网络，大大节省编程时间。

(2)利用遗传算法的全局寻优能力，能够弥补BP神经网络容易陷入局部最小值的缺陷，提高了神经网络的逼近能力和预测精度；同时，遗传算法中改进了自适应交叉、变异概率公式，可以防止对优良基因的破坏，保持种群的多样性，提高了神经网络的性能。

(3)通过对河套灌区解放闸灌域的地下水埋深预测，取得了满意的结果。表明本文提出的改进遗传算法优化的BP神经网络具有较高的精度，很好地解决了地下水位与影响因子间复杂的非线性关系。

(4)改进遗传算法优化的BP神经网络在预测精度上仍有一定的提升空间，在优化BP神经网络阈值、权值方面还可采用蚁群算法、粒子群算法等智能算法。

[1] 屈忠义, 陈亚新, 史海滨, 等.内蒙古河套灌区节水灌溉工程实施后地下水变化的BP模型预测[J]. 农业工程学报, 2003,19(1):59-62.

[2] 刘海军. 塔里木河下游输水条件下的地下水位动态变化与模拟----以英苏断面为例[D]. 乌鲁木齐:新疆大学, 2010:30-44.

[3] 宋 宇, 陈家军, 孙 熊.基于小波函数的地下水水位预测[J].工程勘察, 2006,(4):20-22,29.

[4] 杨志霞.用时间序列模型预测深层地下水位[J].河北水利, 2007,(12):26-27.

[5] 龙 文, 梁昔明, 龙祖强，等. PSO-LSSVM灰色组合模型在地下水埋深预测中的应用[J]. 系统工程理论与实践, 2013,33(1):43-248.

[6] 刘晓丽.移动平均法在地下水位动态预测中的应用[J].地下水, 2014,36(4):85-86.

[7] 张兴鲁.灰色模型在地下水位预测中的应用[J].青海地质, 1991,(1):37-42.

[8] 许 骥.基于遗传BP神经网络的地下水位预测模型[J].地下水, 2015,37(3):19-21.

[9] 张德丰.MATLAB神经网络应用设计[M].北京: 机械工业出版社,2009.

[10] 魏铁军, 王永成, 刘 东.BP网络在三江平原井灌区地下水埋深预测中的应用[J].黑龙江水专报, 2009,36(1):26-30.

[11] 邢贞相.遗传算法与BP模型的改进及其在水资源工程中的应用[D]. 哈尔滨: 东北林业大学, 2004.

[12] 屈忠义.基于人工神经网络理论的区域水-土(盐)环境预测研究[D]. 呼和浩特: 内蒙古农业大学, 2003.

[13] Saeed Bahrami, Faramarz Doulati Ardejani, Ernest Baafi.Application of artificial neural network coupled with genetic algorithm and simulated annealing to solve groundwater inflow problem to an advancing open pit mine[J].Journal of Hydrology, 2016,536:471-484.

[14] 曹道友.基于改进遗传算法的应用研究[D]. 合肥：安徽大学, 2010.

[15] 吴建生.基于遗传算法的BP神经网络气象预报建模[D]. 广西桂林:广西师范大学, 2004.

[16] 高瑞忠.加速遗传算法和自适应人工神经网络模型在地下水系统计算中的应用研究[D]. 呼和浩特:内蒙古农业大学, 2006.

[17] 迟宝明, 林 岚, 丁元芳.基于遗传算法的BP神经网络模型在地下水动态预测中的应用研究[J].工程勘察, 2008,(9):36-41.

[18] 闫凌飞.基于社交网络与遗传算法土壤成分含量研究[D]. 长春:吉林大学, 2004.

[19] 孙 玥.一种改进的遗传算法的实现及其在烟草种植土壤分析中的应用[D]. 长春:吉林大学, 2012.

[20] 李 欣. 自适应遗传算法的改进与研究[D]. 南京:南京信息工程大学, 2008.

[21] 吴建生. 基于遗传算法的BP神经网络气象预报建模[D]. 广西桂林：广西师范大学,2004.

[22] 李 晔. 基于一种改进遗传算法的神经网络[D]. 太原：太原理工大学,2007.