支持向量机的盐碱土壤Philip入渗模型参数预测研究

程诗念，樊贵盛

(太原理工大学水利科学与工程学院，太原 030024)

随着人口的增长和经济的发展，盐碱地的开发利用越来越受到各学者的关注。在广大科技工作者的不断探索与努力下，关于盐碱地的改良已积累了丰富经验，但冲洗方法是主要措施之一。郑普山、郝保平[1]等通过野外试验与室内分析，探究了不同改良剂对盐碱土壤理化性状的影响，进而影响入渗能力或参数。谭丹、谭芳[2]对冲洗条件下盐碱土壤水盐运移进行了模拟得到了盐碱地改良下的优化配水方式。黄圣楠、陈刚[3]等利用一维圆柱形渗流柱，在人为降雨、淋滤条件下，对土壤排盐过程中水盐运移特性进行了研究。目前，关于盐碱地的改良主要分为物理措施、化学措施、生物措施以及相结合的综合措施[4]。其中，因物理方法操作简单、取材容易、投入低下而得到广泛推广，其土壤水动力学原理是通过改变土壤物理性状来调控土壤水盐运移，从而提高入渗淋盐效果，达到降低土壤盐分的目的。因此，盐碱地土壤水分入渗的研究对指导盐碱地的改良意义重大，盐碱土壤入渗参数的准确获取成为改良盐碱地的关键。

支持向量机(Support Vector Machine，SVM)是一种基于结构风险最小化原理的机器学习方法，能在模型的复杂性与学习能力之间找到一个最优折衷，使结构风险最小化，从而获得最佳泛化能力，与模糊逻辑法、人工神经网络等方法相比，在很多方面都表现出其特有的优势，因而备受各学者关注。将该方法应用于土壤水力学参数的预测进一步丰富了土壤转换函数[5]，杨绍锷、黄元仿[6]基于支持向量机建立了预测土壤饱和导水率、残余含水率等水力学参数的土壤转换函数，表明应用支持向量机预测土壤水力学参数是可行的。郑立华、李民赞[7]等采用近红外光谱数据，建立了土壤全氮和有机质含量的支持向量机回归模型，表明土壤参数适合于全谱支持向量回归。

为进一步推广支持向量机算法，并探究获取盐碱土壤水分入渗参数的新方法，本文以盐碱土壤水分入渗试验数据为基础，采用支持向量机回归算法，以Philip入渗模型参数为预测变量，建立回归预测模型，以期获得高精度的预测，研究成果可为盐碱地土壤改良提供技术参数与理论指导。

1 材料与方法

1.1 试验区概况

试验区位于山西省朔州东部的应县，E112°58′～113°37′，N39°17′～39°45′之间，属北温带大陆气候；该地区气候寒冷，年平均气温不高于8 ℃，干旱多风，年降雨量300～400 mm；同时受季风影响，在季节性干旱和降雨条件下，地下水埋深为1.5～2.0 m；地区地形复杂，排水条件差，形成了大面积的原生盐碱荒地。

为获取更广泛的盐碱土壤入渗数据，试验在臧寨、杏寨、大黄崴、大临河四个乡镇展开。试验区土壤母质以近代河流冲积物为主，根据国际制土壤质地分级标准划分，土壤质地均为砂质壤土。土壤颗粒以砂粒为主，其质量分数约占60%。土壤含盐量为1.151～5.143 g/kg，pH值均大于7，全为盐碱土壤。试验区耕作层土壤体积含水率为4.12%～25.86%，容重为1.15～1.85 g/cm3，有机质含量为0.416～1.467 g/kg。

1.2 试验方法

入渗试验采用大田双套环单点入渗仪，试验前在保证地表土壤不受扰动的情况下进行简单处理后将双套环埋在深为20 cm左右的土层中。试验开始后，用1 000 mL量筒分时段向入渗仪内缓慢加水，加水过程确保地表土壤不受冲击，并通过自制水位控制器来调控内外环的入渗水头差，始终保持在2～3 cm，以保证一维垂直入渗。入渗过程中，0～10 min，每1 min记录一次；10～60 min，每5 min记录一次；60～90 min，每10 min记录一次，试验历时90 min。

在入渗试验点采用土钻法获取土壤样本用以测定对应土壤基本理化参数，其中土壤含水率的测定通过称重法、有机质的测定采用重铬酸钾容量法，土壤全盐量采用残渣烘干法，具体操作参见中国农业出版社出版的《土壤农化分析》[8]第三版；土壤容重测定采用环刀法；土壤质地分析采用激光粒度分析仪；土壤pH通过pH计测定，水土比2.5∶1，具体步骤参照文献[9]。

1.3 Philip入渗模型

1957年，基于非饱和半无限土壤垂直入渗条件，Philip[10]根据土壤水分运动方程的级数解推导得到在短历时入渗情况下，任意时刻的入渗率i(t)与入渗时间t之间满足幂级数关系，关系式为：

(1)

式中：i(t)为t时刻的入渗率，cm/min；S为吸渗率，cm/min0.5；A为稳定入渗率，cm/min。

根据上式，对时间t积分，即可得出累积入渗量I(t)与入渗历时t之间的关系：

I(t)=St0.5+At

(2)

式(1)和式(2)共同构成了Philip入渗模型，本文选择描述式(2)作为研究模型。

2 基于支持向量机的盐碱土壤入渗参数预测

2.1 建立数据样本

根据所取得的入渗过程资料，即累积入渗量I(t)与入渗历时t之间的对应关系，利用Matlab2009中的非线性拟合工具，拟合得到Philip入渗模型参数，即吸渗率S和稳渗率A。将取得的S和A与在试验区同步测定的土壤基本理化参数结合，建立土壤基本理化参数与入渗参数之间的一一对应关系，完成试验样本的建立，本文建立了100组试验样本，如表1所示。

表1 试验样本数据表

2.2 支持向量机预测模型的建立

本文选取盐碱土壤体积含水率θ0、干容重γ1、有机质含量G、粉粒含量w1、黏粒含量w2、全盐量δ和pH值ε为输入变量，Philip水分入渗模型的吸渗率S和稳渗率A为输出变量，建立预测模型。选择90组试验数据样本作为建模样本，10组作为验证样本。

首先将输入样本x通过非线性函数φ(x)映射到高维空间，然后建立如下回归函数：

f(ω,x)=ωφ(x)+b

(3)

式中：ω为权值向量；b为阈值。

已知样本集{(x1，y1) (x2，y2) (x3，y3)…(xm，ym)}(m为样本组个数，本文训练样本的组数为90，检验样本的组数为10)，其中xi∈Rn(i=1，2，…，m)为输入向量，此处为土壤基本理化参数值，n表示输入向量的维数，也就是输入变量的个数，此处n=7；yi∈R(i=1，2，…，m)为输出变量，本文为Philip土壤水分入渗模型中的吸渗率S和稳渗率A。

引入拟合误差函数ε、惩罚因子C和松弛变量ξ、ξ*(ξ、ξ*≥0)，由此最佳回归函数转化为求解式(4)的最小值：

(4)

对应的约束条件为：

(5)

引入拉格朗日乘子，将其转化为二次对偶形式，通过解对偶问题即可得到式(3)的解：

(6)

式中：αi、α*i(αi、α*i≥0)为拉格朗日乘子；k(x,xi)为核函数，应满足Mercer条件。

式(6)即为本文所建立的预测模型。

2.3 支持向量机参数的确定

付阳[12]等认为影响支持向量机预测模型精度的主要因素为：核函数、惩罚因子C和函数拟合误差ε。

(1)核函数的选择。常用的核函数主要有线性核函数、多项式核函数、径向基核函数。本文采用交叉验证法，以平均相对误差(MRE)作为评价指标，在保证其他参数一定，只改变核函数的情况下，经过试算，最后选取平均相对误差最小的径向基核函数作为支持向量机预测模型的核函数，其表达式为：

k(xi,xj)=exp(-g‖xi-xj‖) (g=1.0)

(7)

(2)惩罚因子C和拟合误差ε的选取。参数C和ε权衡了最大空白和最小训练误差，进而影响着训练与预测精度。

ε为函数拟合误差，其值的改变影响着模型结构的复杂程度。ε值过大，模型结构趋于简单，支持向量个数会越少，算法在拟合数据过程中会出现压力不足现象，将导致拟合误差大；ε值过小，虽能提高拟合精度，但模型结构会过于复杂，有可能造成运算速度降低，导致训练时间过长, 模型泛化能力较差，有可能导致将会出现过拟合现象。

因个别样本数据的严重偏离，而引入的惩罚因子C可以用于控制模型复杂度和逼近误差的折中。C越大，也就是惩罚力度越大，模型的复杂程度越高，容易出现“过学习”。而C值过小，会导致对经验误差的惩罚偏小，模型的复杂程度降低，有可能造成“欠学习”。如果直接剔除偏差样本，虽在一定程度上会提高训练模型对自身数据的学习精度，但将其应用于其他数据进行预测时，精度会有所降低。

基于此，在确定核函数为径向基核函数的前提下，进行多次试算，并利用多参数网格搜索法对参数C和ε进行优化选取，最后取C=100，ε=0.05。

2.4 预测结果分析

将模型参数值带入回归算法中，利用Matlab2009进行回归预测，经过分析，得到训练样本和检验样本的相对误差如表2和表3所示。

表2 训练样本相对误差表

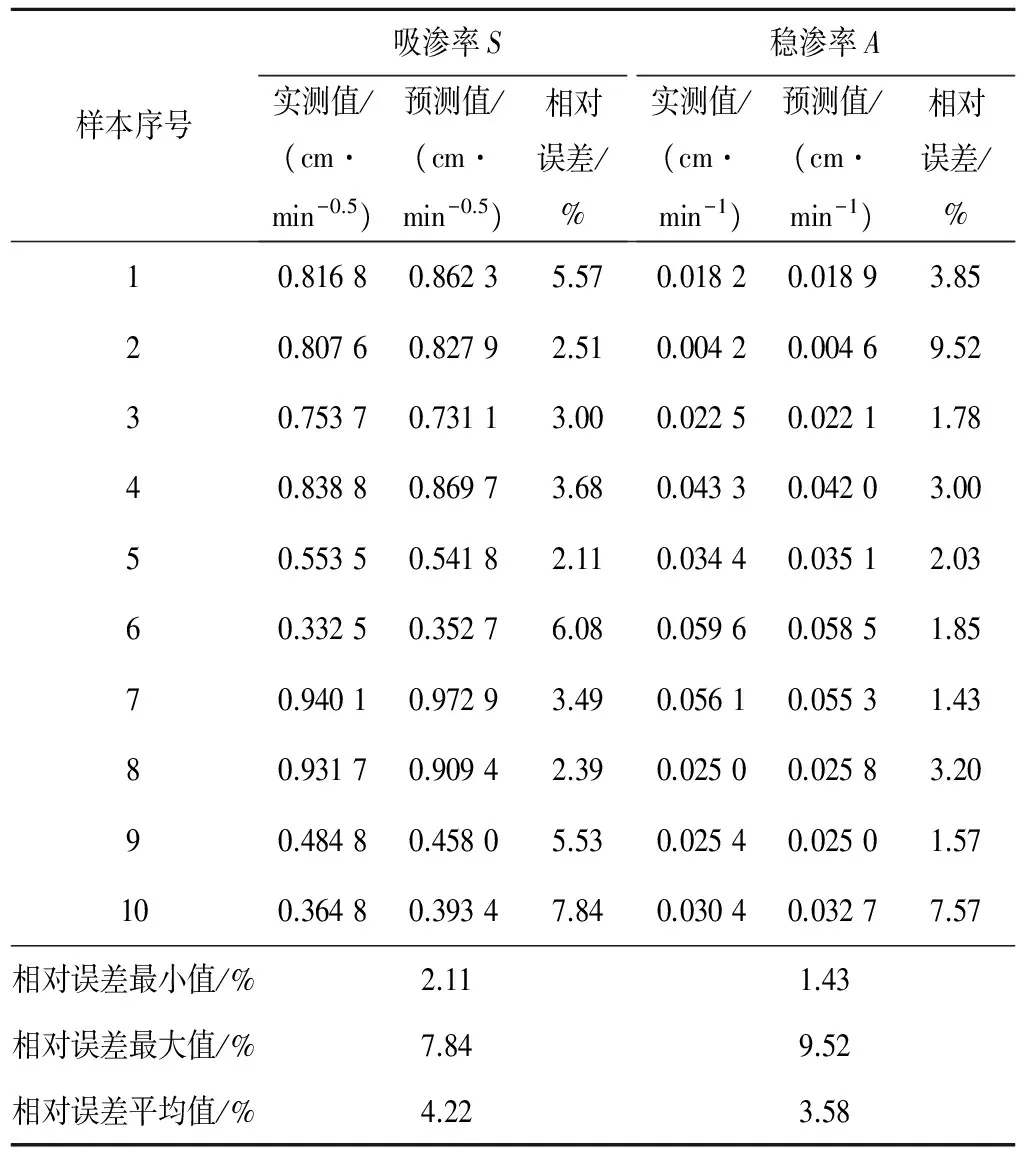
表3 检验样本相对误差表

从表2和表3可以看出：吸渗率S训练样本相对误差的最小值为0.04%，最大值为9.75%，平均值为4.05%；检验样本相对误差的最小值为2.11%，最大值为7.84%，平均值为4.22%。稳渗率A训练样本相对误差的最小值为1.07%，最大值为11.53%，平均值为5.49%；检验样本相对误差的最小值为1.43%，最大值为9.52%，平均值为3.58%。不论是训练样本还是检验样本，两入渗参数的平均相对误差值均较小，预测值与实测值之间吻合程度高，预测精度较高，建立的预测模型是可行的。

2.5 综合误差分析

依据预测得到的Philip入渗模型参数，得到Philip入渗模型的预测表达式，通过计算可得90 min累积入渗量I90的预测值，与实测值相比较，计算相对误差，得到训练样本和检验样本中两入渗参数的综合误差分析表，如表4和表5所示。

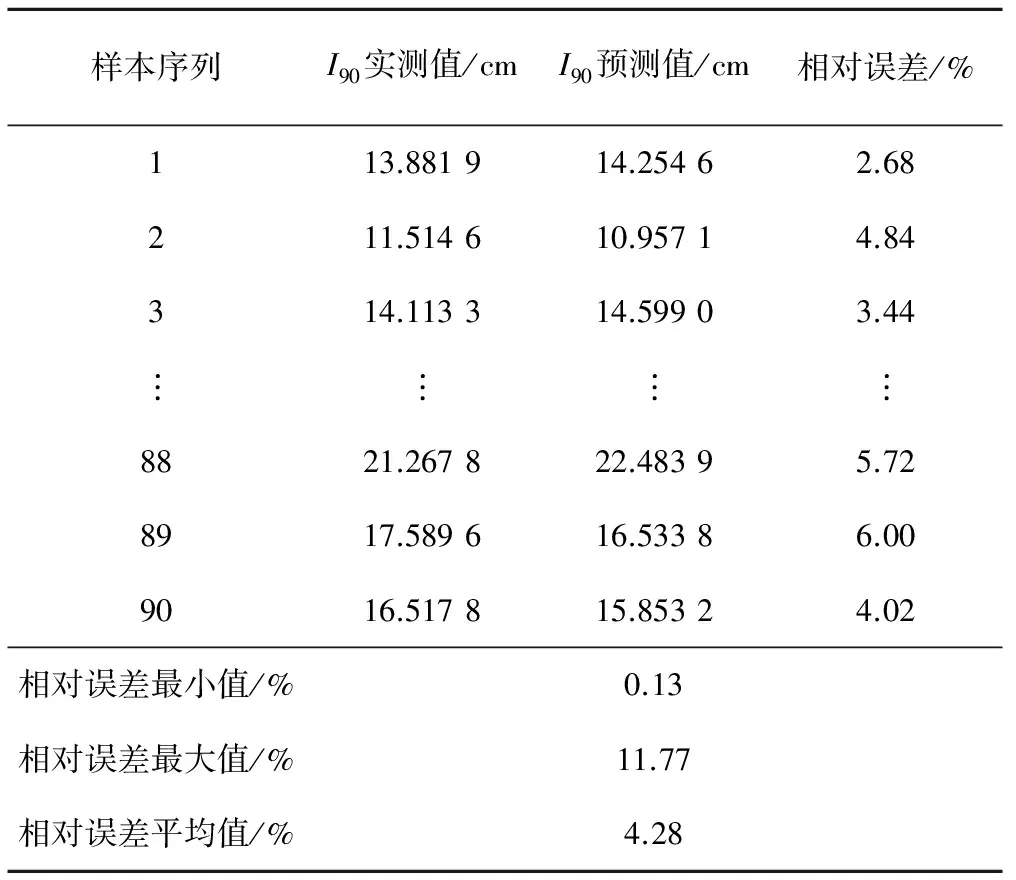
表4 训练样本I90误差分析表

表5 检验样本I90误差分析表

从表4和表5可以看出：90组训练样本中，根据Philip两入渗参数计算得到的累积入渗量I90的预测值与实测值相比较，相对误差的最小值为0.13%，最大值为11.77%，平均值为4.28%；10组检验样本中，90 min累积入渗量I90的预测值与实测值相比较，相对误差的最小值为0.28%，最大值为8.75%，平均值为4.48%，可以看出两参数的综合误差值较小，表明所建立的模型能实现对Philip入渗模型参数的高精度预测。

3 结 语

(1)基于支持向量机理论，对Philip入渗模型参数进行预测，以平均相对误差作为评价指标，吸渗率S的训练误差为4.05%，检验误差为4.22%；稳渗率A的训练误差为1.07%，检验误差为3.58%；两入渗参数综合误差90 min累积入渗量I90的训练误差为4.28%，检验误差为4.48%。训练样本和检验样本误差均较小，能满足精度要求，表明基于支持向量机理论的盐碱土Philip入渗模型参数的预测是可行的。

(2)由模型得到的Philip入渗模型中的吸渗率S、稳渗率A以及90 min累积入渗量I90的预测值与实测值吻合程度高，预测效果理想，实现了支持向量机预测模型对盐碱土壤入渗参数的预测。

本文是针对盐碱土壤，基于支持向量机算法对Philip入渗模型参数的初次尝试，模型中有关参数的选择、输入参数的选取等都有待进一步的研究，以期获取更精准的预测结果，丰富支持向量机算法的研究领域。

[1] 郑普山,郝保平,冯悦晨,等.不同盐碱地改良剂对土壤理化性质、紫花苜蓿生长及产量的影响[J].中国生态农业学报,2012,20(9):1 216-1 221.

[2] 谭 丹,谭 芳.明沟排水条件下盐碱地改良优化配水模式[J].灌溉排水学报,2008,28(1):97-100.

[3] 黄圣楠,陈 刚,丁国平,等.滩涂盐碱土一维渗透淋滤试验与排盐效果分析[J].安全与环境工程,2014,21(2):64-67.

[4] 马 晨,马履一,刘太祥,等.盐碱地改良利用技术研究进展[J].世界林业研究,2010,23(2):28-32.

[5] 黄元仿,李韵珠.土壤水力性质的估算——土壤转换函数[J].土壤学报,2002,39(4):517-523.

[6] 杨绍锷,黄元仿.基于支持向量机的土壤水力学参数预测[J].农业工程学报,2003,23(7):42-47.

[7] 郑立华,李民赞,安晓飞,等.基于近红外光谱和支持向量机的土壤参数预测[J].农业工程学报,2010,26(S2):81-87.

[8] 南京农业大学. 土壤农化分析[M]. 北京: 中国农业出版社, 1986.

[9] NY/T 1377-2007, 土壤pH的测定[S].

[10] PHILIP J R．The theory of infiltration about sorptivity and algebraic infiltration equations[J]. Soi Sci., 1957,84(4):257-264.

[11] 原林虎. PHILIP入渗模型参数预报模型研究与应用[D]. 太原：太原理工大学, 2013.

[12] 付 阳,李昆仑.支持向量机模型参数选择方法综述[J].电脑知识与技术,2010,6(10):8 081-8 082,8 085.