多孔喷嘴能量转化效率分析

李敬彬，李根生，黄中伟，宋先知

(中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249)

设计计算

多孔喷嘴能量转化效率分析

李敬彬，李根生，黄中伟，宋先知

(中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249)

多孔喷嘴是径向水平井技术的核心技术装备，需同时实现高效破岩与强力自进，而目前常用的多孔喷嘴的流量系数一般在0.6左右，其能量转换效率仅为36%左右，严重限制了多孔喷嘴的整体性能。因此，研究多孔喷嘴流量系数影响规律十分必要。根据流量系数定义推导了多孔喷嘴流量系数，试验确定了各孔眼局部阻力系数，并研究了排量、孔眼数量对多孔喷嘴流量系数影响规律。结果表明，多孔喷嘴能量转化效率等于其流量系数的平方；其流量系数由各孔眼流量系数与其权重决定；孔眼流量系数主要取决于其沿程阻力系数与局部阻力系数；绝大部分能量损失由局部阻力损失引起；而孔眼局部阻力系数随着排量增加略有降低，但随着孔眼数目增加而迅速增大。

径向水平井；多孔喷嘴；喷嘴流量系数；能量转换效率

1 前言

径向水平井技术可在储层不同层面沿径向钻出多个径向水平分支井眼，是20世纪80年代提出的一种油气田增产开发技术[1,2]，已在美国、加拿大、中国、阿根廷、埃及以及玻利维亚等国家应用或实验，效果明显[3～7]。该技术仅依靠射流破岩喷嘴完成高效破岩与连续钻进，使其成为径向水平井技术的关键设备[8]。但受到现场排量以及压力条件的限制，现有水力破岩喷嘴很难满足应用要求。因此，设计优化出一种自进式高效水力破岩喷嘴具有重大意义。

多孔喷嘴是一种应用于径向水平井技术的高效射流钻头(如图1)，主要由中心孔眼、前向孔眼与后向孔眼组成。其工作原理为：前向孔眼以冲击破碎作用形成一个较大水平孔眼，后向孔眼则依靠射流反冲作用提供自进力，同时起到扩充井眼的作用。目前，已有学者针对多孔喷嘴破岩性能与自进能力进行了大量研究：P Buset等研究了多股射流破岩机理与自进力产生机理[9]；廖华林等通过实验研究了孔眼数目和水力参数对其破岩效果的影响规律[10]；马东军等通过理论分析与室内实验的方法对其自进力产生机理与自进力影响规律进行了研究[11]。但室内试验研究表明，多孔喷嘴流量系数大多在0.5～0.6之间，能量转换效率仅有36%。因此，十分有必要开展多孔喷嘴能量转化效率研究。

图1 多孔喷嘴结构示意

2 喷嘴流量系数与能量转换效率的关系

根据钻头压降公式有：

(1)

式中 Δp——喷嘴压降，Paρ——流体密度，kg/m3Q——流体排量，m3/sC——喷嘴流量系数，无因次Ane——出口当量面积，m2

由连续性方程得：

(2)

将式(2)代入式(1)并整理得：

(3)

由式(3)可得，高压流体经喷嘴作用后，仅有C2倍的压能转化为流体的动能，C2表示了喷嘴能量的转化效率，是喷嘴水力性能的重要指标。因此，有必要开展多孔喷嘴流量系数相关研究，提高水力能量利用效率。

3 多孔喷嘴流量系数计算公式推导

3.1 多孔喷嘴结构及工作原理

多孔喷嘴内部结构如图1所示。多孔喷嘴主要由一个中心孔眼、n2个前向孔眼与n3个后向孔眼组成，其对应的孔眼直径、平均流速、排量分别为di，vi，Qi(i=1,2,3)，另外，前后向孔眼轴线与多孔喷嘴轴线夹角分别为θ2，θ3，喷嘴的入口直径d0，入流平均速度v0，入流压力p0，流体流量Q0，出口压力pout。由于多孔喷嘴需要完成水力破岩，故其射流速度较高，其射流流态一般为紊流，且认为各孔眼速度等于其平均速度。本文以后向孔眼数目+前向孔眼数目+中心孔眼数目来命名，即n3+n2+1。

3.2 多孔喷嘴能量损失分析

在锥形喷嘴流量系数的研究中，将锥形喷嘴看作一个渐缩管，流体通过喷嘴的主要能量损失包括沿程能量损失与收缩损失[12,13]。

与此类似，将多孔喷嘴看作若干突缩管的组合。通过多孔喷嘴的能量损失主要包括沿程能量损失和局部能量损失。

(1)沿程能量损失分析

将各孔眼内的流动看作圆管流动，沿程能量损失按照圆管紊流沿程水力损失计算，其计算公式如下：

(4)

式中hf——沿程能量损失λ——沿程阻力系数[14]

L——圆管长度

v——圆管内平均流速

d——圆管直径

g——重力加速

(2)局部阻力损失分析

由于多孔喷嘴不存在导流段，因此无法将多孔喷嘴看作渐缩管进行分析。其局部能量损失由液流断面急剧变化以及液流方向转变引起，因此可将多孔喷嘴看作多个突缩管的组合。则其局部能量损失按照突缩管局部能量损失计算，其计算公式如下[15～19]：

(5)

式中hj——局部能量损失ζ——局部阻力系数v′——孔眼内平均流速g——重力加速

对于无转角圆形管路突然缩小局部阻力系数只有经验公式进行计算，其常用计算公式如下[19]：

(6)

式中A2——小管截面积A1——大管截面积

但根据袁恩熙等的研究表明，突缩管的局部阻力系数随着小直径圆管内的流速增加逐渐降低[14]。因此局部阻力系数变化复杂，特别是多孔喷嘴存在3组不同的局部阻力系数，其值只能通过试验测得。

3.3 多孔喷嘴流量系数推导

多孔喷嘴结构如图1所示，分别在0-0断面与1-1断面、2-2断面、3-3断面间，分别建立伯努利方程：

(7)

式中p0——喷嘴入口压力 γ——流体重度α0，αi——动能修正系数，喷嘴内流动为紊流，α0=αi≈1

v0，vi——喷嘴入口和各孔眼的平均流速

pout——喷嘴出口压力，一般取大气压，即pout=0

通常情况下，孔眼内的流体流速远大于喷嘴内的流速，即vi>10v0，因此v0项可忽略；且流量系数测量多在大气中进行，则有pout=0。并将式(4)、式(5)代入式(7)得：

(8)

根据之前的分析将各孔眼的排量与速度关系代入式(8)可得：

(9)

各孔眼截面积与当量截面积之间存在以下关系：

(10)

式中dne——当量直径

由式(9)与式(10)可得通过各孔眼的排量：

(11)

根据连续方程可得：

Q0=Q1+n2Q2+n3Q3

(12)

式(11)代入式(12)，并整理得：

(13)

若流体为理想流体，则其排量为：

(14)

喷嘴流量系数是流过喷嘴的实际流体的流量与理想流体的流量之比，因此可得多孔喷嘴的流量系数定义式：

C=Q0/Q′0

(15)

通常情况下，多孔喷嘴前后孔眼直径相等，则式(15)可进一步简化为：

(16)

由式(16)看出，多孔喷嘴的流量系数为各孔眼的流量系数的比重组合，孔眼流量系数及其数量决定了多孔喷嘴的流量系数；当孔眼数量一定时，流量系数较大的孔眼比重越大越有利于改善多孔喷嘴流量系数。各孔眼流量系数主要取决于其沿程阻力与局部阻力，但由于多孔喷嘴各孔眼长度通常较小，则可推测其沿程阻力较小；因此应着重研究局部阻力的影响因素，局部阻力主要由液流截面急剧变化以及液流方向改变引起，则局部阻力与孔眼直径有关，孔眼直径越大越有利于降低局部阻力；同时，有研究表明孔眼内流速越高，局部阻力越小；并且局部阻力与流场复杂程度有关，流场越复杂局部阻力系数越大。但由于局部阻力系数变化复杂，所以式(16)无法直接用于计算多孔喷嘴流量系数，只能定性的分析多孔喷嘴各结构参数对其喷嘴流量系数的影响，需通过室内实验进行验证与测定局部阻力系数。

4 多孔喷嘴流量系数测试试验

4.1 试验设备

(1)高压柱塞泵

额定压力为60 MPa，额定排量为100 L/min，柴油机功率为90 kW，并可通过其发动机转速得到排量。

(2)压力传感器

传感器量程为30 MPa，输出电流4～20 mA，测量精度为0.1%F*S，安装于泵头，通过减去高压软管沿程压耗可得喷嘴压降。

(3)多孔喷嘴

设计并加工了多孔喷嘴，如图2所示，其具体参数如下：d0=9.5 mm，d1=d2=d3=1.0 mm，n2=3，n3=6，θ2=12°，θ3=30°。通常以后向孔眼数目+前向孔眼数目+中心孔眼数目命名多孔喷嘴，本次加工的多孔喷嘴称为6+3+1型喷嘴。

图2 多孔喷嘴实物

4.2 试验方案

根据流量系数计算式：

(17)

式中ρ——流体密度，kg/m3Q——射流排量，m3/s Δp——射流压力，MPaA——出口当量面积，m2

由此，对于一个特定喷嘴，仅需测量其在不同排量下的射流压力，通过式(17)即可获得喷嘴的喷嘴流量系数。试验电焊堵眼的方法，实现了6+3+1，6+2+1，6+1+1，6+0+1，6+0+0不同型号的喷嘴，研究了不同孔眼数目喷嘴流量系数变化规律。为确保试验的准确性，每种型号喷嘴分别测试多组排量下的喷嘴流量系数，分别计算喷嘴流量系数。

5 试验结果分析

5.1 喷嘴流量压力关系

通过室内试验，得到了不同型号喷嘴的流量-压力曲线，如图3所示。

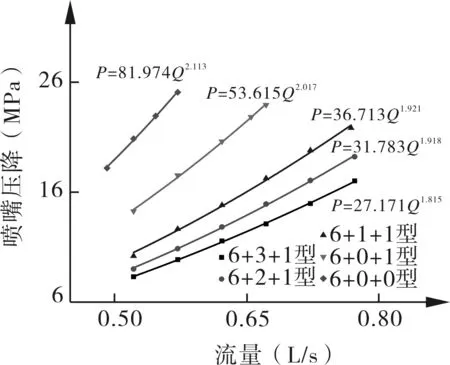
图3 不同型号喷嘴流量-压力曲线

从图3可知，各喷嘴的射流压力与射流排量存在近似二次方关系，并不完全符合喷嘴压降公式，这说明随着排量的变化多孔喷嘴流量系数并不是一个常数，这与锥形喷嘴有很大的区别。当喷嘴孔眼较多时，喷嘴压降随流量变化缓慢，因此在安全压力范围内测试了6组流量条件下喷嘴压降；随着孔眼数目减少，多孔喷嘴流压曲线开始逐渐陡峭，喷嘴压降随流量迅速增大，因此，6+0+0型喷嘴仅测试4组小排量情况下的喷嘴压降，可见随着孔眼数量的减少，导致当量直径减小，安全压力下允许的流量减小，井下水力能量减小，不利于多孔喷嘴的高效破岩与自进。

5.2 流量对喷嘴流量系数影响

多孔喷嘴与锥形喷嘴不同，不存在导流段，流体流经多孔喷嘴时，类似于流过多个并联突缩管路，由孔径突然缩小引起的局部阻力造成了较大的能量损失；但突缩管的局部阻力系数随着排量的增加会减小，因此有必要研究流量对多孔喷嘴流量系数的影响规律。根据式(17)及多孔喷嘴流量压力数据，可得各多孔喷嘴流量系数随流量变化曲线，如图4所示。

图4 各喷嘴流量系数随流量变化曲线

从图可知，多孔喷嘴流量系数均低于0.6，仅有不到36%的水力能量转换为流体的动能，转换效率极低，由此可见其水力性能亟待改善；同时，各型多孔喷嘴流量系数随排量均有小幅度增加，但增加幅度不是很大；且孔眼数目越多喷嘴流量系数受排量影响越大，以6+3+1型多孔喷嘴为例，排量从0.522 L/s增大至0.772 L/s时，其喷嘴流量系数增加达3.3%。由此可得，随着排量的增大有利于各孔眼局部阻力系数减小，进而改善多孔喷嘴水力性能，这与之前的分析一致。但其增幅较小，因此不能够通过提高排量来提高多孔喷嘴的水力性能，必须从多孔喷嘴结构上改善其水力性能。

5.3 孔眼数目对喷嘴流量系数影响

由于向前的孔眼流量系数大于后向孔眼流量系数，在保证自进力的条件下，向前的孔眼数量越多，多孔喷嘴的流量系数应该越大，但试验中发现其随向前的孔眼数量的变化并不是单调递增的关系。由图4可得，各型多孔喷嘴流量系数受到排量的影响，但其变化幅度较小，因此取各型多孔喷嘴在不同排量条件下平均流量系数进行分析。图5所示为不同喷嘴的流量系数随孔眼数量的变化规律。从图中可得，随着向前的孔眼数目的增多，喷嘴流量系数先增大后减小，这主要是由于随着单孔流量系数较大的向前的孔眼数目的增多，多孔喷嘴的水力性能得到改善，喷嘴的流量系数增大；但随着孔眼数目的增多，喷嘴内部流场更加复杂导致各孔眼处局部阻力系数不断增加，导致喷嘴流量系数将减小，甚至低于仅有后向孔眼的喷嘴，多孔喷嘴的水力性能受到严重影响。因此，在进行多孔喷嘴设计时，应在保证多孔喷嘴其破岩能力与自进能力的基础上，增加单孔直径，减少孔眼数目，并通过室内测试得到最佳孔眼组合，更加高效的利用水力能量。

图5 多孔喷嘴流量系数随向前的孔眼数目变化曲线

5.4 孔眼数量对局部阻力系数影响

试验用多孔喷嘴结构参数如下：喷嘴直径d0=9.5 mm；各孔眼直径d1=d2=d3=1.0 mm，前向孔眼与后向孔眼数目及角度n2=3，n3=6，θ2=12°，θ3=30°；各孔眼长度L1=3.0 mm，L2=3.5 mm，L3=4.5 mm；各孔眼与清洁无缝钢管类似，取其表面绝对粗糙度△=0.01 mm；计算得到沿程阻力系数λ=0.038；中心孔眼局部阻力系数可通过式(6)进行估算，可得ζ1=0.415，由于各孔眼直径相等，仅是角度的不同，故其局部阻力系数存在一定函数关系，其值与各孔眼轴线与喷嘴轴线夹角有关，且可以推断后向孔眼阻力系数均比前向孔眼阻力系数大，则有：ζ2=α2ζ1，ζ3=α3ζ1，α3>α2>1，其中α2、α3均为与前后孔眼角度有关的无量纲常数。

试验过程中通过堵眼实现不同的喷嘴结构，当只有后向孔眼时，根据式(16)可得到后向孔眼的局部阻力系数ζ3=2.229，由此可得α3=5.371；由于难以准确求取前向孔眼局部阻力系数，通过线性差分可得α2=1.350，由此可得到其近似值。根据各型号多孔喷嘴流量系数及式(16)可得各孔眼局部阻力系数，结果如表1所示。

表1 各型号多孔喷嘴单孔眼局部阻力系数

以6+0+1型多孔喷嘴的前向孔眼为例，其中局部阻力ζ1=0.477，而沿程阻力λ1L1/d1=0.114，可见局部阻力至少是沿程阻力的4.18倍，由此可得，多孔喷嘴主要的压力损失由局部阻力造成。

由于中心孔眼、前向孔眼、后向孔眼局部阻力系数之间存在线性关系，则在研究孔眼数目对孔眼局部阻力系数的影响时，仅对中心孔眼局部阻力系数随孔眼数目变化进行分析，其结果如图6所示。从图中可以看出，随着向前的孔眼数目的增多，中心孔眼局部阻力系数成迅速增大，这主要是因为随着孔眼数目增加，流场结构越来越复杂，导致单孔眼局部阻力系数增大，最终导致多孔喷嘴整体水力性能的下降，即喷嘴流量系数的降低，这与之前的分析一致，即当随着单孔眼流量系数较大的向前的孔眼比重增大，多孔喷嘴流量系数逐渐增大，但同时由于流场结构越来越复杂，导致单孔眼流量系数均减小，并最终导致多孔喷嘴流量系数的降低，且随着孔眼数量的增加，流场复杂性的影响越来越明显，导致本文中6+3+1喷嘴流量系数甚至低于6+0+0的喷嘴流量系数。

图6 中心孔眼局部阻力系数随向前的孔眼数目变化曲线

6 结论

(1)多孔喷嘴能量转化效率等于其流量系数的平方，能量转化效率较低。

(2)多孔喷嘴流量系数为各孔眼流量系数权重组合，当孔眼数量一定时，流量系数较大的孔眼比重越大越有利于改善多孔喷嘴流量系数。

(3)多孔喷嘴绝大部分水力损失由局部阻力引起，严重影响了多孔喷嘴水力性能。

(4)随着排量增大，各孔眼局部阻力系数降低，但影响幅度不大；但随着孔眼数目的增加，各孔眼的局部阻力系数迅速增大，严重影响多孔喷嘴水力性能。

(5)在多孔喷嘴设计时，应在保证破岩成孔与自进能力的前提下，尽量增大单孔直径，改善单孔眼水力性能，减少孔眼数目，室内试验测试最佳孔眼组合，以提高喷嘴流量系数，进而提高水力能量的利用效率。

[1] Dickinson W,Dickinson R W.1985.Horizontal radial drilling system[C].Presented at the SPE California Regional Meeting,Bakersfield,California,27-29 March.SPE-13949-MS.

[2] Dickinson W,Anderson R R,Dickinson R W.The ultrashort-radius radial system[J].SPE Drilling Engineering,1989,4(03): 247-254.SPE-14804-PA.

[3] Dickinson W,Dykstra H,Nees J M,et al.1992.The ultrashort radius radial system applied to thermal recovery of heavy oil[C].Presented at the SPE Western Regional Meeting,Bakersfield,California,30 March-1 April.SPE-24087-MS.

[4] Bruni M A,Biasotti J H,Salomone G D.2007.Radial drilling in argentina[C].Presented at the Latin American & Caribbean Petroleum Engineering Conference,Buenos Aires,Argentina,15-18 April.SPE-107382-MS.

[5] Cirigliano R A,Blacutt J F T.2007.First Experience in the application of radial perforation technology in deep wells[C].Presented at the Latin American & Caribbean Petroleum Engineering Conference,Buenos Aires,Argentina,15-18 April.SPE-107182-MS.

[6] Abdel-Ghany M A,Siso S,Hassan A M,et al.New technology application,radial drilling petrobel,first well in egypt[C].Presented at the Offshore Mediterranean Conference,Ravenna,Italy,23-25 March.OMC-2011-163.

[7] 施连海,李永和,郭红峰.径向水平井技术在锦45-检1井中的应用[J].石油钻探技术,2002,30(5):23-24.

[8] 曹立刚.煤层气井短半径水平钻井技术研究[J].中国煤田地质,2003,15(3):19-21.

[9] Buset P,Riiber M,Eek A.2001.Jet drilling tool: cost-effective lateral drilling technology for enhanced oil recovery[C].Presented at the SPE/ICoTA Coiled Tubing Roundtable,Houston,Texas,7-8 March.SPE-68504-MS.

[10] 廖华林,牛继磊,程宇雄,等.多孔喷嘴破岩钻孔特性的实验研究[J].煤炭学报,2011,36(11):1858-1862.

[11] 马东军,李根生,黄中伟,等.自进式多孔射流钻头的自进机理及自进力影响规律[J].天然气工业,2014,34(4):99-104.

[12] 刘成文,李兆敏.锥形喷嘴流量系数及水力参数的理论计算方法[J].钻采工艺,2000,23(5):1-3.

[13] 杨友胜,张建平,聂松林.水射流喷嘴能量损失研究[J].机械工程学报,2013,49(2):139-145.

[14] 袁恩熙.工程流体力学[M].北京:石油工业出版社,1986: 121-131.

[15] 李敬彬，李根生，黄中伟，等.新型旋转射流多孔喷嘴流场的分析[J].流体机械，2015，43(7)：32-36.

[16] 毕刚，李根生，沈忠厚，等.径向水平井自进式旋转射流钻头流场特性分析[J].流体机械，2014，42(5)：25-30.

[17] 宋利滨，马源，吴泽敏.圆螺纹油管上扣扭矩计算方法[J].压力容器，2014，31(4)：75-79.

[18] 曹敏，张文普，贫油直喷燃烧室回火的数值研究[J].机电工程，2014，31(9)：1111-1116.

[19] 吴持恭.水力学(上册)[M].北京:高等教育出版社,2007: 129-155.

Energy Conversion Efficiency of the Multi-orificenozzle

LI Jin-bin,LI Gen-sheng,HUANG Zhong-wei,SONG Xian-zhi

(State Key Laboratory of Petroleum Resources and Prospecting,China University of Petroleum,Beijing 102249,China)

As the “core” of radial jet drilling (RJD) technology,the multi-orifice nozzle must forcefully self-feed and effectively break the rock to form a radial hole.But nozzle discharge coefficient of the multi-orifice nozzleis always smaller than 0.6 in most cases that means only less than 36 percent hydraulic energy transfers to the fluid.It is extremely important to study the changing law of the nozzle discharge coefficient of the multi-orifice nozzle.According to the definition of nozzle discharge coefficient,its exact expression of the multi-orifice nozzle was derived.Local resistance coefficient and effects of numbers of orifice and flow rate on the nozzle discharge coefficient werestudied by experiment.Results show that the square of the nozzle discharge coefficient represents the energy conversion efficiency of the multi-orifice nozzle;the nozzle discharge coefficient of multi-orifice nozzle depends on the discharge coefficient and weight ratio of the single orifice;the discharge coefficient of each orifice lies on the frictional resistant coefficient and the local resistance coefficient;most of the energy loss of each orifice wascaused by local resistance;local resistancewould slightly decrease with flow rate while greatly increase with the number of orifice.

radial jet drilling;multi-orifice nozzle;nozzle discharge coefficient;energy conversion efficiency

1005-0329(2017)01-0020-06

2016-03-30

2016-07-29

国家863计划项目(2015AA043401)；国家科技重大专项(2011ZX05036002)；中国石油大学(北京)科学基金项目(2462013BJRC002)

TH3

A

10.3969/j.issn.1005-0329.2017.01.004

李敬彬(1989-)，男，在读博士研究生，研究方向为微小井眼径向水平钻井和相关技术，通讯地址：102249 北京市昌平区府学路18号 中国石油大学工程学院，E-mail:lijingbin555@hotmail.com。