超大跨度门式刚架斜梁塑性设计
姜继红, 梁汇溪, 李 贞(沈阳大学 建筑工程学院, 辽宁 沈阳 110044)
超大跨度门式刚架斜梁塑性设计
姜继红, 梁汇溪, 李 贞
(沈阳大学 建筑工程学院, 辽宁 沈阳 110044)
结合超大跨度门式刚架工程实际,利用PKPM软件对钢结构超大跨度门式刚架斜梁进行弹塑性设计和塑性设计,数值分析模拟得出截面几何特性是确定截面塑性的重要参数.
钢结构; 超大跨度门式刚架; 斜梁; 塑性分析
目前,我国钢产量逐年提高,而钢材价格较前些年也有明显下降,钢结构的应用形式在不断的改革创新,近几年钢结构成为了我国新兴的热门结构形式.钢结构由于自身的诸多优点,已经成为我国土木行业里最具发展潜力的结构类型.钢结构的设计方法有弹塑性设计法和塑性设计法两种.弹塑性设计法普遍认为应力到达弹性极限,在进入到塑性变形阶段时,材料即将发生破坏,此时结构已经失效,所以弹塑性设计法往往是控制最大内力截面上的最大应力不超过材料的强度设计值.实际上,当结构局部材料进入塑性变形阶段的时候,应力就会出现重分布,使应力分布更为均匀,从而提高结构的承载能力.通过以上理论证明,以塑性理论为基础的设计相比较于弹塑性设计更为经济,更加发挥了材料的潜力[1].因此,钢结构的塑性设计研究就变得十分重要.
1 塑性理论分析概述
1.1 塑性理论概念
结构的塑性设计就是考虑一定数目的截面形成了塑性铰,使结构整体或局部变为机构从而导致破坏,以此作为承载力极限状态进行设计.首先要确定结构破坏时,结构所能承担的载荷----极限载荷[2],然后通过载荷系数的换算计算得出容许载荷作为结构设计依据.要想确定极限载荷,则必须考虑材料塑性变形,进行结构的塑性分析.
1.2 塑性理论分析的特点
塑性理论分析主要具有以下特点:
(1) 结构物经常遇到难以预测的由于沉陷、制造等因素所造成的大应力.塑性设计更为贴近结构的实际情况,能更准确表现出结构的真实承载力.
(2) 相比于弹塑性设计分析,塑性设计的结构分析更为简便,这一优势在超静定次数越多时,就越有明显的体现,因此设计者不仅可以通过准确的估计结构物承受最大载重,而且能够极大的缩短设计时间.
(3) 塑性设计可以节约钢材用量,在通常情况下相比弹塑性设计耗钢量,塑性设计可节约用钢量10%~20%[1].
1.3 塑性理论分析应用条件
现行《钢结构设计规范》GB50017—2003在塑性设计中明确规定,塑性设计适用于不直接承受动力载荷的固端梁、连续梁以及由实腹式构件组成的单层和两层框架结构[3].在对规范的进一步学习和研读过程后,对于塑性设计的应用条件作出以下总结:
(1) 构件的局部失稳在结构达到塑性重分布之前坚决不允许发生,虽在局部失稳后仍有些强度可利用,但承载力达不到截面完全塑性时的强度,容易导致塑性发展进程中承载力的衰退.
(2) 整体失稳不能在结构形成机构前发生,理论数据分析得出,整体失稳将直接导致承载力的下降.
(3) 不能够采用格构式构件,因为此构件在边缘屈服后向腹部发生塑性的余地很少,难以完成内力塑性重分布.
(4) 不能选用沿杆件截面连续变化或突然变化的杆件.
(5) 采用塑性设计时,直接承受动力载荷的构件不宜选用[2].
2 受弯构件塑性理论分析性能
2.1 受弯构件塑性理论分析过程
对受弯构件进行塑性理论分析,在研究受弯构件弯曲正应力时,根据平面假设可以断定在构件的中间部位必然有一层完全没有变化的纵向“纤维”,这一纵向“纤维”层即是中性层,中性层与横截面的交线则为中性轴[4].如图1所示.
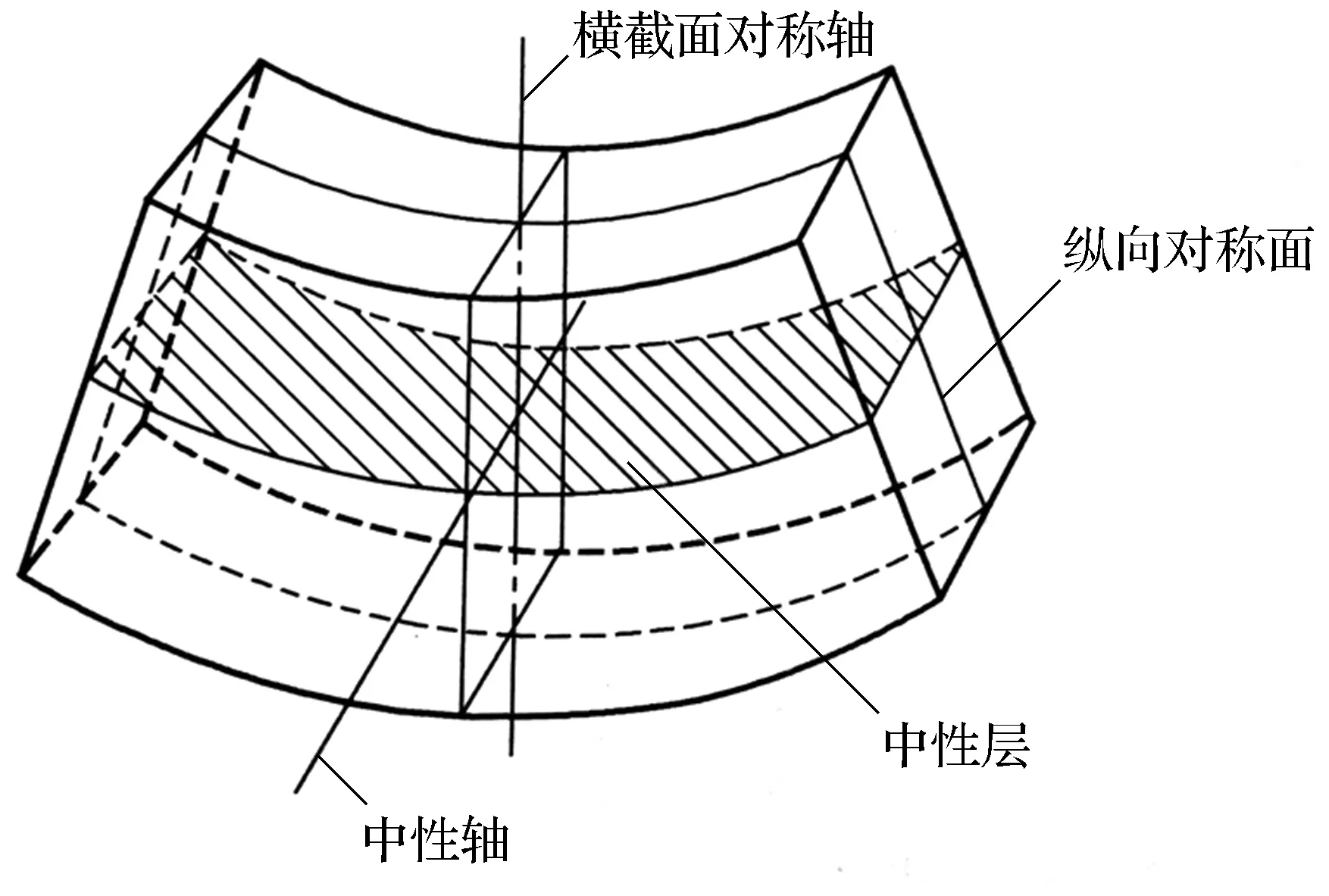
图1 在平面假设下梁受弯内部“纤维”Fig.1 Internal “fiber” of beam bending under plane assumption
在横截面内建立Ozy坐标系,则其中性层的曲率为
式(1)表明,构件弯曲变形后曲率随着弯矩M的变大而变大、随弯矩M的变小而变小,随着EIZ的变大而变小、随EIZ的变小而变大.
由单向受力假设可知,在应力小于比例极限的情况下,利用胡克定律可得公式
将式(1)带入式(2),可得弯曲正应力计算公式
式中:M为横截面上的弯矩;IZ为横截面对中性轴Z的惯性矩;y为点的纵坐标,即点到中性轴Z距离.
通过式(3)中弯矩M与点的纵坐标y的正负可以确定某点的应力是拉还是压.区分出拉压应力后,在计算时就不用考虑计算式中M与y的正负号了.
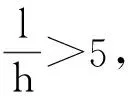
由式(3)可知,当y=ymax,即在横截面上距离中性轴z最远的上、下边缘各点处,弯曲正应力有最大值,为
令
则式(4)可改写为
式中,WZ称为抗弯截面系数,它取决于截面的几何形状与尺寸.
确定弯曲正应力的最大值后,即得弯曲正应力强度条件
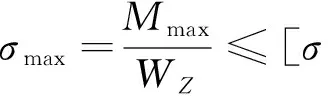
在计算承受相等的拉伸许用应力和压缩许用应力的塑性材料时,可以运用该公式来进行计算[4].从该公式中可以看出WZ越大则其应力强度越小,反之WZ越小则其应力强度越大.而WZ又与杆件截面强度有关,由此可知受弯构件的弯曲应力与杆件截面的几何性质有关.在现行《钢结构设计规范》GB 50017—2003第九章塑性设计在构件的计算中也提出弯矩Mx(对H形和工字形截面x轴为强轴)作用在一个主平面内的受弯构件,其弯曲强度应符合下式要求:
式中,Wpnx为对x轴的塑性净截面模量[3].
在此式中也表明了弯曲强度与Wpnx有关,取决于杆件的截面尺寸,因此截面几何特征值是确定截面塑性的重要参数.
2.2 截面几何特征值的计算
在对各种截面进行塑性设计时首先要做的就是对其截面力学几何特征值进行计算,在计算截面特征值时主要计算内容为其截面的惯性矩、截面系数、和截面的回转半径.
(1) 截面惯性矩的计算公式
截面对任一轴的惯性矩:等于各微面积dA与它到该轴距离平方的乘积的总和,如图2所示,即
(9)
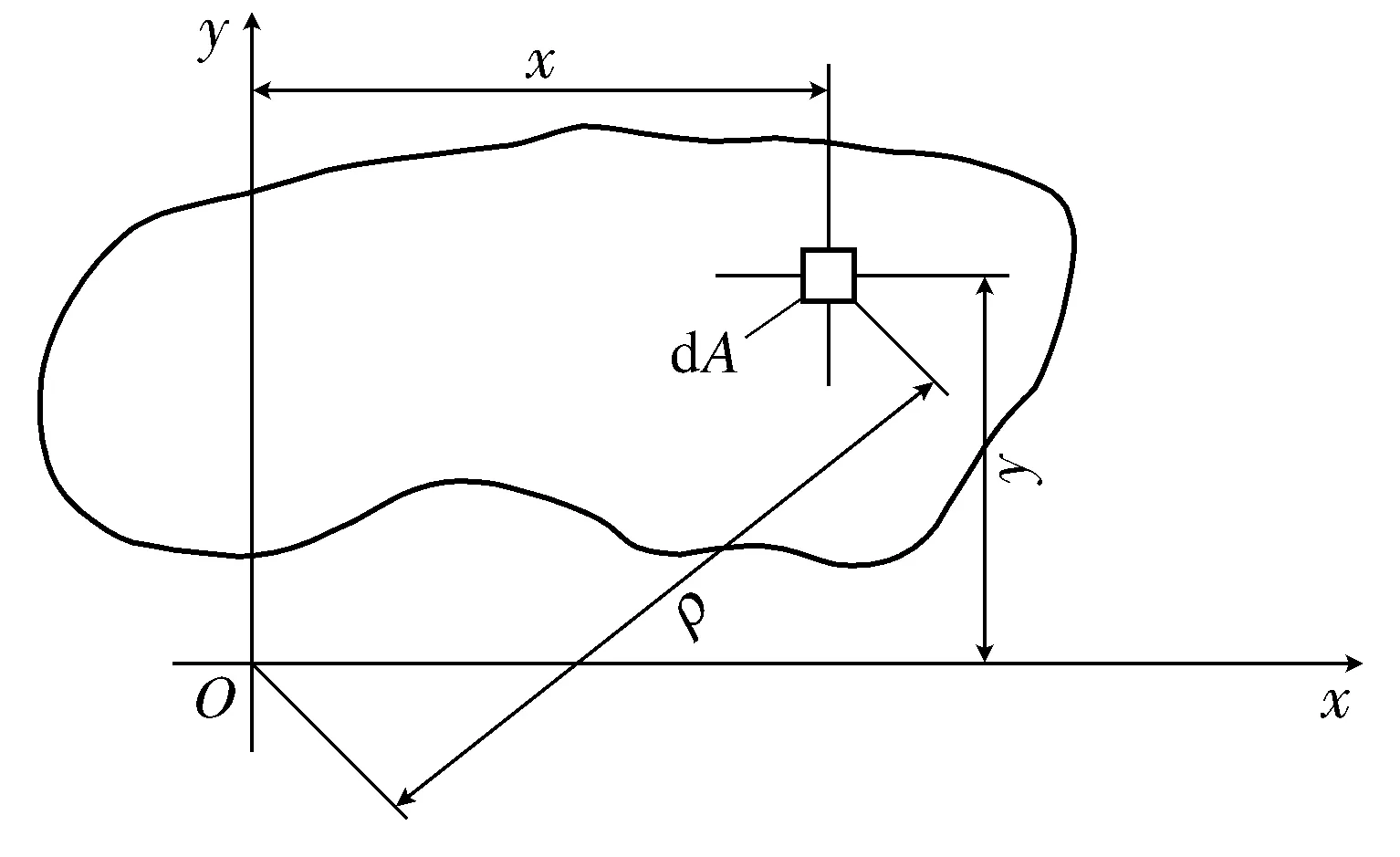
图2 截面对任一轴的惯性矩Fig.2 Moment of inertia of cross section to any axis
平行轴惯性矩间的关系如图3所示.设o点为截面的形心,x轴和y轴为截面的形心轴.截面对平行于形心轴x和y轴而相距a和b的x′和y′轴的惯性矩为:
式中,A为截面积.
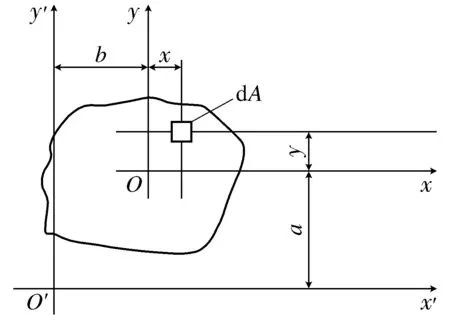
图3 平行轴惯性矩间的关系Fig.3 The relationship between inertia moment of parallel axis
(2) 截面系数的计算如图4所示.
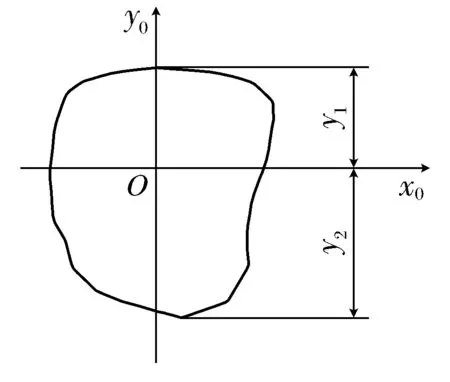
图4 截面系数的计算公式Fig.4 Calculation formula of cross section coefficient
式中:Wx1,Wx2分别为截面上、下边缘的截面系数;Ix0为截面对形心轴x0的惯性矩;y1、y2分别为形心到截面上边缘及下边缘的距离.
(3) 截面的回转半径的计算公式
式中:ix为截面对x轴的回转半径;Ix为截面对x轴的惯性矩;A为截面积[5]
以H形为例计算其截面力学特性,过程如下,其截面见图5.
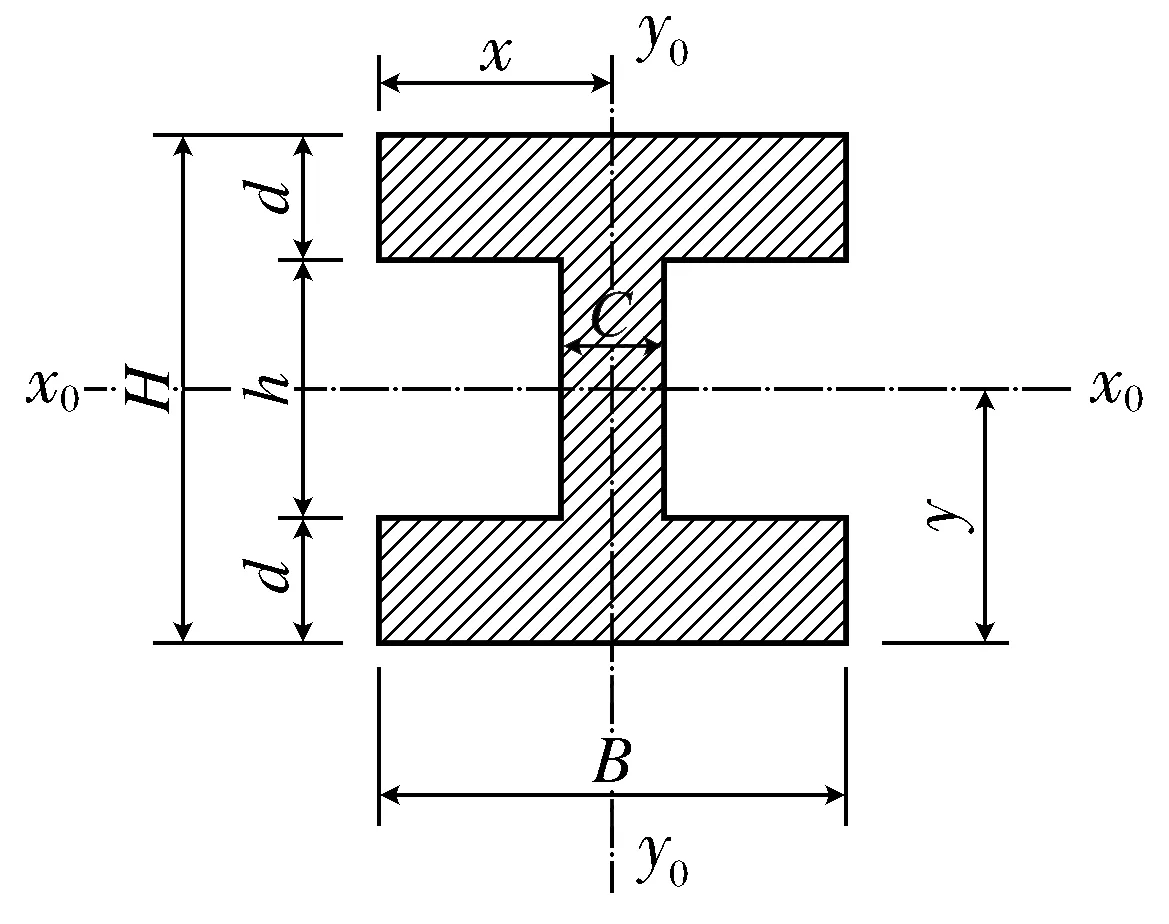
图5 H形截面简图Fig.5 H shape section diagram
截面积:A=Ch+2Bd
轴线至边缘距离:
同样的方法,通过计算可得出以下几种不同截面的力学特性.如表1.
3 刚架斜梁塑性设计性能比较
3.1 刚架斜梁
单层门式钢架是一种轻型房屋结构体系,它的主要承重骨架为以轻型焊接H型钢(等截面或变截面)、 热轧H型钢 (等截面)或冷弯薄壁型钢等构成的实腹式门式刚架或格构式门式刚架,其檩条、墙梁为冷弯薄壁型钢(槽形、卷边槽形、Z形等)做成,屋面、墙面用压型金属板(压型钢板、压型铝板)来进行制作,并且它的保温隔热材料是采用聚苯乙烯泡沫塑料、硬质聚氨酯泡沫塑料、岩棉、矿棉、玻璃棉来制作[6].
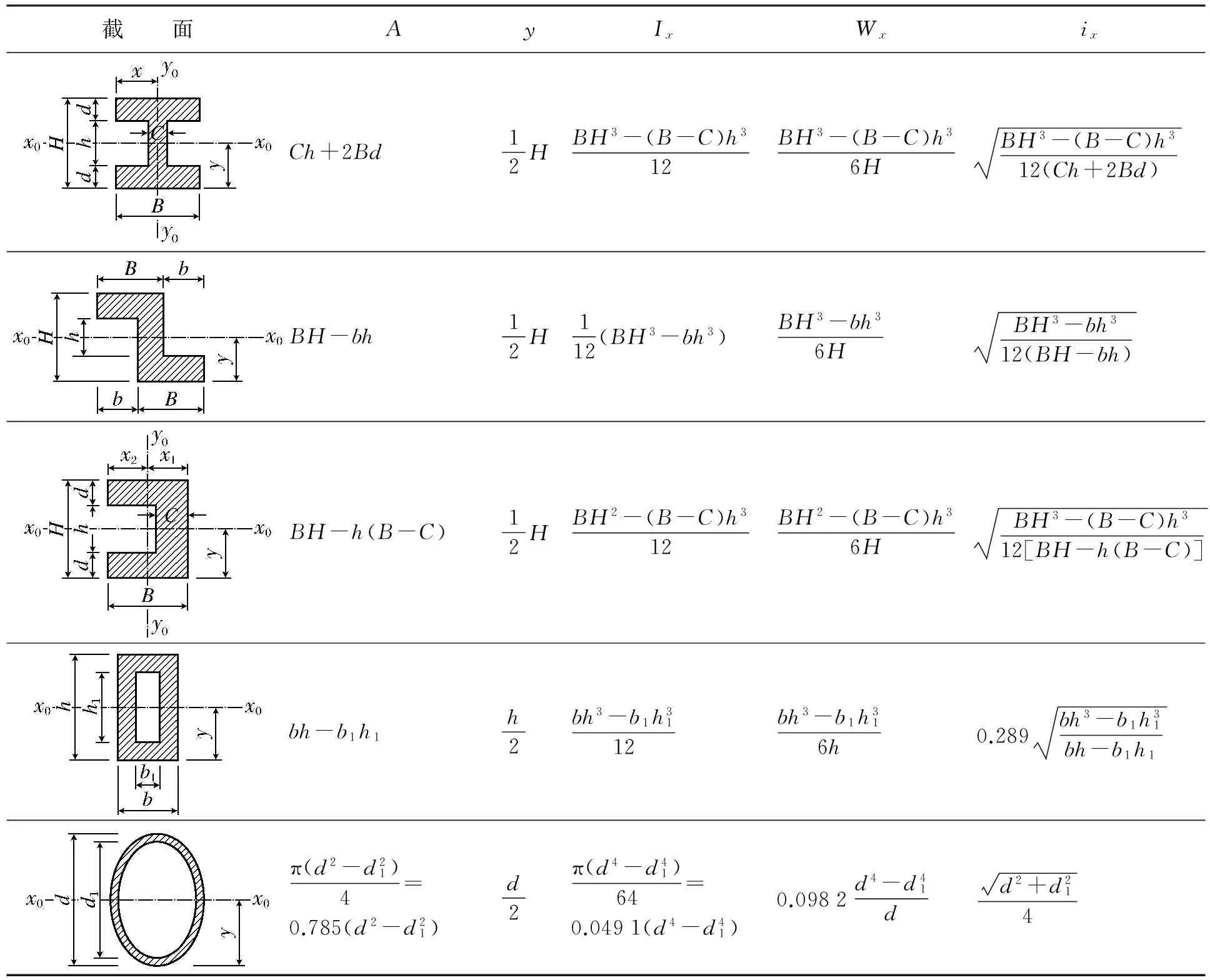
表1 截面力学性能Table 1 Mechanical properties of the cross section
目前,门式刚架轻型房屋结构在轻型厂房、大型超市、体育馆、仓库、交易市场、展览厅及活动房屋、加层建筑等建筑的应用很广泛[6].
在门式刚架中,由于排水要求,斜梁在安装时有一定的坡度,并且需要檩条的支撑,这些都会使得斜梁承受一定的轴力,因此斜梁所承受的力主要有弯矩,剪力和轴力,这些力使得斜梁在计算时与普通梁有区别.
3.2 斜梁的弹塑性与塑性设计计算公式比较
斜梁设计进行时主要有两种设计方法,一种是传统的设计方法弹塑性设计,另一种是塑性设计方法.这两种设计方法在进行设计计算时的区别主要是在强度设计计算和局部稳定设计计算两个方面.
3.2.1 抗剪强度计算比较
塑性设计方法计算抗剪强度,通常采用下式
式中:hw、tw分别为腹板高度和厚度;V为计算截面沿腹板平面作用的剪力设计值;fv为钢材的抗剪强度设计值.
弹塑性设计方法计算抗剪强度时主要是满足:
式中:V为计算截面沿腹板平面作用的剪力设计值;S为计算剪应力处以上毛截面对中利轴的面积矩;I为毛截面惯性矩;tw为腹板厚度;fv为钢材的抗剪强度设计值.
3.2.2 抗弯强度计算比较
塑性设计方法计算抗弯强度通常采用
式中:Mu为同一截面处绕x轴的弯矩;Wpnx为对x轴的塑性净截面模量;fy为弹塑性设计方法计算抗弯强度时,需满足
式中:Mu为同一截面处绕x轴的弯矩;Wnx为对x轴的净截面模量;γx为截面塑性发展系数,对工字形截,γx=1.05,不同截面类型则不同;f为钢材的抗弯强度设计值.
3.3 斜梁的弹塑性与塑性设计工程实例比较
本工程系铁岭东北物流城一期,建材大市场C馆,厂房跨度为119 m,总长度为239 m,结构体系采用不规则的轻型门式刚架结构,单层多跨,单跨度为40 m,已经超过《门式刚架轻型房屋钢结构技术规程》规定的刚架最大跨度为36 m,间距20 m,共14榀刚架,檐口高度为10 m,屋面坡度为1:8,刚架斜梁为6跨双坡,坡度为1:8.平面布置图见图6,结构立面图见图7.
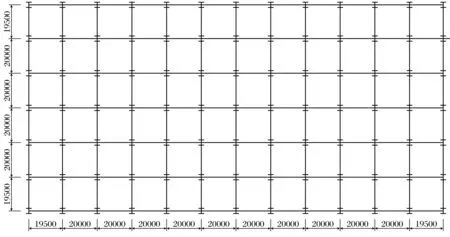
图6 平面布置图(单位:mm)Fig.6 Floor plan(unit: mm)
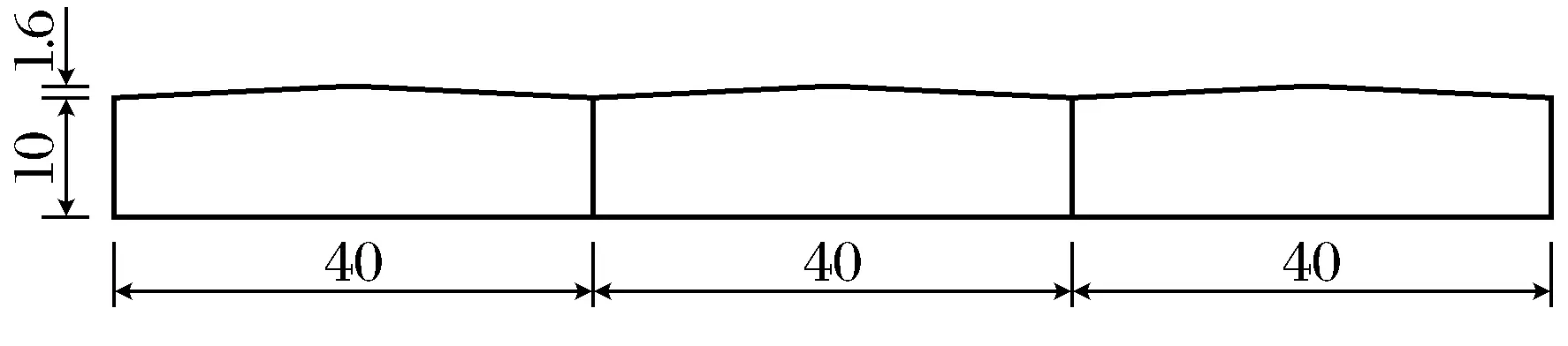
图7 结构立面图(单位:m)Fig.7 Elevation of the structure(unit: m)
在该工程中斜梁为Q345的H型钢截面如图8所示,结合实际工程斜梁所采用的H型钢,对该截面分别按照弹塑性设计和塑性设计计算其极限承载能力.
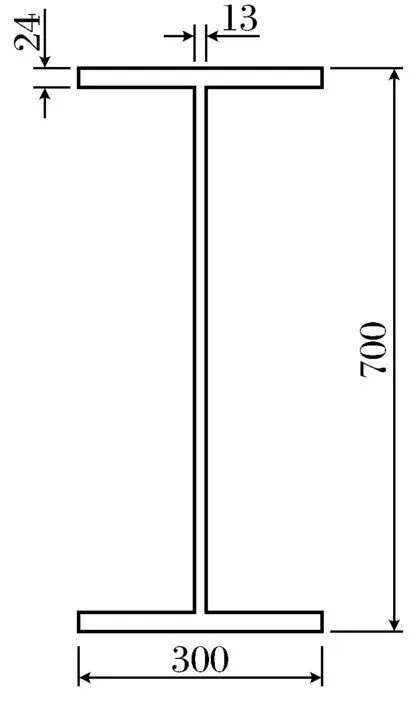
图8 Q345 H型钢截面(单位:mm)Fig.8 Section of Q345 H-beam(unit: mm)
按照弹塑性理论计算其极限承载力
按照塑性理论计算其极限承载力
由此可以得出,通过塑性理论设计所得出的极限承载力要大于弹塑性理论设计得出的极限承载力值,按照塑性设计则可以降低截面的高度或者降低厚度来使极限承载力降低,从而使材料承载力利用更加充分.
3.4 不同截面的塑性设计比较
结合具体工程实际情况,对该结构斜梁采用三种不同截面进行的塑性设计比较.
对于不同截面在相同力作用下的强度可以根据刚架梁构件强度计算公式来进行手算,也可以利用PKPM电算来进行.
当手算时工字形截面受弯构件在剪力和弯矩共同作用下的强度应符合下列要求:
当V≤0.5Vd时,M≤Me;
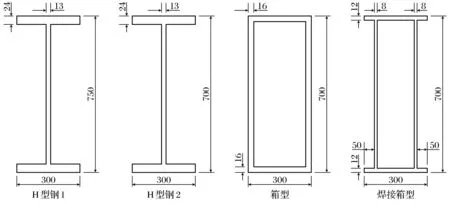
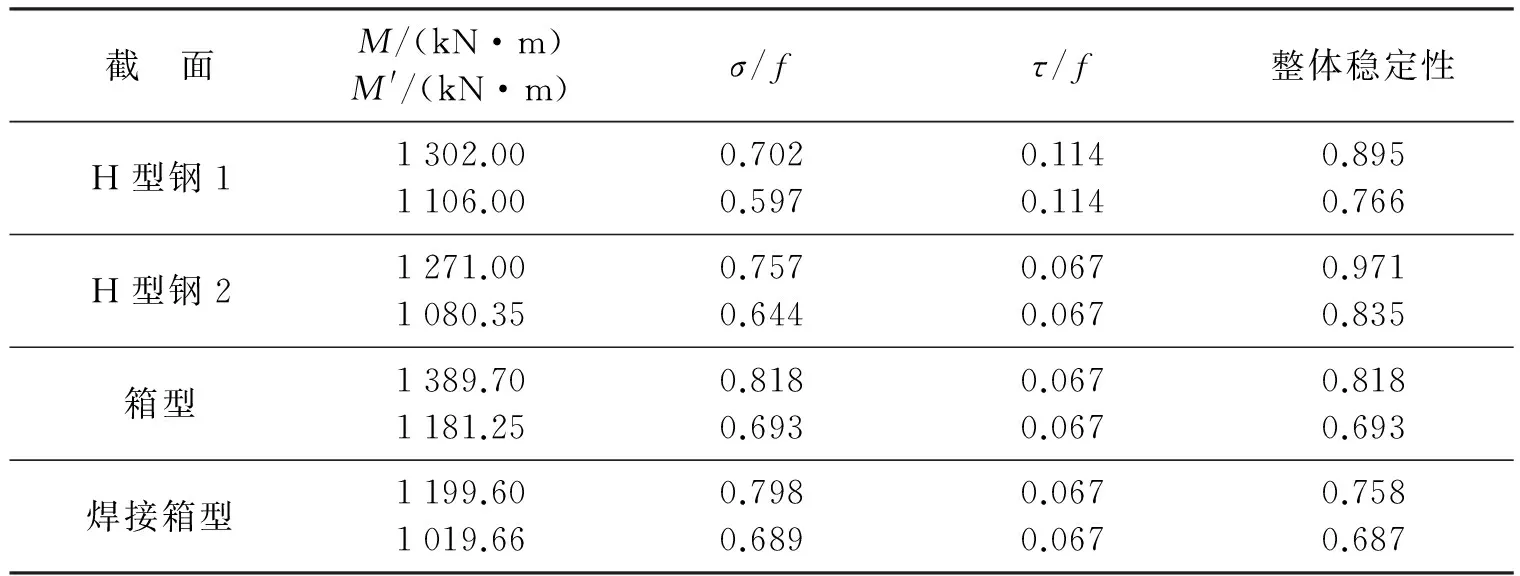
当0.5Vd 当截面为双轴对称时 式中:Mf为两翼缘所承担的弯矩;Me为构件有效截面所承担的弯矩,Me=Wef;We为构件有效截面积最大受压纤维的截面模量;Af为构件翼缘的截面面积;Vd为腹板抗剪承载力设计值. 工字形截面受弯构件在剪力、弯矩和轴力共同作用下的强度应符合下列要求: 当0.5Vd (20) 当截面为双轴对称时, 对该工程的斜梁采用不同截面进行设计得出,截面选取合适尺寸使得设计最佳,各截面尺寸及截面属性分别如图9和表2所示. 图9 不同截面的尺寸(单位:mm)Fig.9 Sizes of different cross section(unit: mm) 表2 不同截面的截面特性Table 2 Cross section characteristics of different cross section 根据实际工程状况,当其他所有条件均相同而斜梁使用不同的截面的钢材时,利用PKPM对不同截面进行设计电算,对不同截面使用情况及截面特性进行分析. 当斜梁使用不同截面,综合比较使用不同截面时的应力比.如表3所示. 表3 截面各应力比Table 3 Stress ratio of the cross section 通过对几个截面分别进行弹塑性计算和塑性计算的对比可知,在相同内力下,进行塑性调幅后截面的应力比和调幅之前相比要降低很多,说明按照塑性计算截面有更多的承载力可以利用. 通过对塑性理论的分析以及结合工程实际的分析得出,截面几何特性是确定截面塑性的重要参数;对于超大跨度门式刚架的斜梁,塑性设计可使截面承载力提高,从而可通过降低截面高度或截面厚度来节省钢材,降低造价;对于H型钢,箱型钢,焊接箱型钢三种截面进行塑性计算调幅后,其截面有更多的承载力可以利用,说明对截面进行塑性调幅很有必要. [1] 王中华. 钢结构中的塑性设计概念及其应用[J]. 四川建筑科学研究, 2006,32(6):27-30. (WANG Z H. The plastic design concept and application in steel structure[J]. Sichuan Building Science, 2006,32(6):27-30.) [2] 龙驭球. 结构力学教程(下册)[M]. 北京:高等教育出版社, 1988:116-117. (LONG Y Q. Course of structure mechanics (Volume 2)[M]. Beijing: Higher Education Press, 1988:116-117.) [3] 中华人民共和国建设部. 钢结构设计规范: GB 50017—2003[S]. 北京:中国计划出版社, 2003. (Ministry of Construction of the People’s Republic of China. Code for design of steel structures: GB 50017-2003[S]. Beijing: China Planning Press, 2003.) [4] 王永廉. 材料力学[M]. 北京:机械工业出版社, 2008:109-118. (WANG Y L. Mechanics of material[M]. Beijing: Machinery Industry Press, 2008:109-118.) [5] 《建筑结构静力计算手册》编写组. 建筑结构静力计算手册 [M]. 2版. 北京:中国建筑工业出版社, 1998:44-55. (Writing Group. Handbook of static calculation of building structure[M]. 2nd edition. Beijing: China Building Industry Press, 1998:44-55.) [6] 陈绍蕃. 钢结构(下册):房屋建筑钢结构设计[M]. 2版. 北京:中国建筑工业出版社, 2007:1-5. (CHEN S F. Steel structure (Volume 2): Building architecture steel structure design[M]. 2nd edition. Beijing: China Building Industry Press, 2007:1-5.) [7] 戴国欣. 钢结构[M]. 4版. 武汉:武汉理工大学出版社, 2012:217-218. (DAI G X. Steel structure[M]. 4th edition. Wuhan: Wuhan University of Technology Press, 2012:217-218.) [8] 门式刚架轻型房屋钢结构技术规程: CES 102—2002[S]. 北京:中国计划出版社, 2002. (Technical specification for steel structure of light-weight buildings with gabled frames: CES 102-2002[S]. Beijing: China Planning Press, 2002.) [9] 刘晓,杨玲,刘刚. 钢结构体系中梁、柱及节点分析[J]. 沈阳大学学报, 2005,17(6):26-28. (LIU X,YANG L,LIU G. Beam, column and conjunctions of them in steel construction system[J]. Journal of Shenyang University, 2005,17(6):26-28.) [10] 赵柏冬,俞萧,陈培超,等. 高温后钢管钢骨混凝土组合柱轴压的稳定性[J]. 沈阳大学学报(自然科学版), 2015,27(2):151-154. (ZHAO B D,YU X,CHEN P C,et al. Stability of steel tube filled with steel-reinforce concrete subjected to axial compression after high temperature[J]. Journal of Shenyang University(Natural Science), 2015,27(2):151-154.) 【责任编辑: 肖景魁】 Plasticity Design of Oblique Beam for Large Span Gantry Frame JiangJihong,LiangHuixi,LiZhen (Architectural and Civil Engineering College, Shenyang University, Shenyang 110044, China) Combining with the engineering practice of large span gantry rigid frame, using PKPM software, the elastic-plastic design and the plastic design of the steel-frame super-span portal frame oblique beam are carried out. The numerical simulation shows that the section geometry is an important parameter to determine the plasticity of the section. steel structure; large span gantry frame; oblique beam; plasticity analysis 2016-09-28 姜继红(1963-),女,辽宁沈阳人,沈阳大学教授. 2095-5456(2017)01-0071-07 TU 393.3 A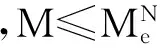
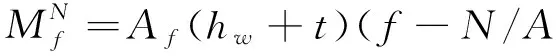
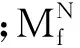

4 结 论

