基于多项式递归更新的高光谱异常检测算法

赵春晖, 邓伟伟(哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001)

基于多项式递归更新的高光谱异常检测算法

赵春晖, 邓伟伟
(哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001)

针对海量数据处理给高光谱图像异常目标检测造成一定干扰的现象,在逐行处理方式上,引入卡尔曼滤波器的递归思想及Woodbury矩阵引理,提出了一种基于多项式递归更新的高光谱异常目标检测算法.实验结果表明,在检测精度保持不变的前提下,提出的算法的运算效率相比于传统算法得到显著提高.

高光谱图像; 异常检测; 逐行处理; 局部窗

高光谱遥感技术的不断发展,使其在农林监控[1]、考古勘探[2]、军事侦察[3]及地质探测[4]等领域得到了广泛应用.高光谱遥感能够同时将地物的一维空间信息和二维光谱信息相结合,探测地物光谱之间的微小差异[5].高光谱目标检测技术是高光谱图像处理领域一个较为活跃的分支.常用高光谱检测算法有Schaum提出的基于光谱维的匹配子空间检测(Matched Subspace Detector, MSD)算法[6]和Chang等人提出的约束最小能量(Constrained Energy Minimization, CEM)算法[7]等,均取得了良好的检测效果,但以上方法需要已知目标的先验信息.然而,在实际应用中,大多数目标的光谱信息受多种复杂因素的影响,并不能准确得知,如光谱数据库信息的不完备和反射率反演算法的不精确等,均对目标的检测和识别带来一定的困扰.因此无需任何目标先验光谱信息的异常检测(Anomaly Detection, AD)更具有实际价值.异常检测主要根据各点光谱特性的差异,统计局部区域内的变化完成异常点的检测.最为经典的异常检测算法是由Reed和Yu提出的基于二值假设检验模型的异常目标检测(RX)算法[8].它通过将背景和目标建模为高斯分布,利用马氏距离来寻找异常目标[9].RX算法由于在进行计算时需要用到全部样本像元的统计信息,算法的时效性较差.

随着高光谱图像数据量的增大,提高异常检测的时效性很有必要.一方面海量数据处理给高光谱数据下行传输造成了一定的压力,对数据存储空间提出了更高的要求;另一方面为避免弱异常目标被后续检测到的强异常目标所干扰,需要对待检测数据同时进行传输和处理,保证检测过程的时效性.目前,推扫型成像光谱仪已成为高光谱空间成像的主要方式,设计基于推扫方式的高光谱快速异常检测算法更具有实际意义.Rossi等人结合线性代数理论,提出一种基于逐行处理的快速RX异常目标检测算法[10],但它的推导过程并未严格按照矩阵进行推导,且推导信息并不完整.为此,本文在逐行处理的基础上,提出一种基于多项式递归更新的高光谱异常检测(BLRXD)算法.该算法采用局部半窗模型完成异常目标的检测,利用卡尔曼滤波器的递归思想以及Woodbury矩阵求逆引理递归更新复杂矩阵的逆矩阵,降低算法的计算复杂度.并利用真实高光谱数据进行实验仿真,验证了算法在时效性上的优越性.

1 RX异常检测算法

RX算法是Reed与Yu基于广义似然比检验(GLRT)提出的一种未知目标未知背景的恒虚警异常检测算法.它在假设背景数据服从高斯分布的前提下,利用图像中对样本像元的统计与估计求得分布中的均值和协方差矩阵.虽然这种假设与真实的图像数据分布有所差异,但在统计特性上,也具有一定的合理性.RX算法以待测像元为中心,确定局部检测窗口.其中待测像元位于内窗中,背景信息位于外窗中,如图1所示.

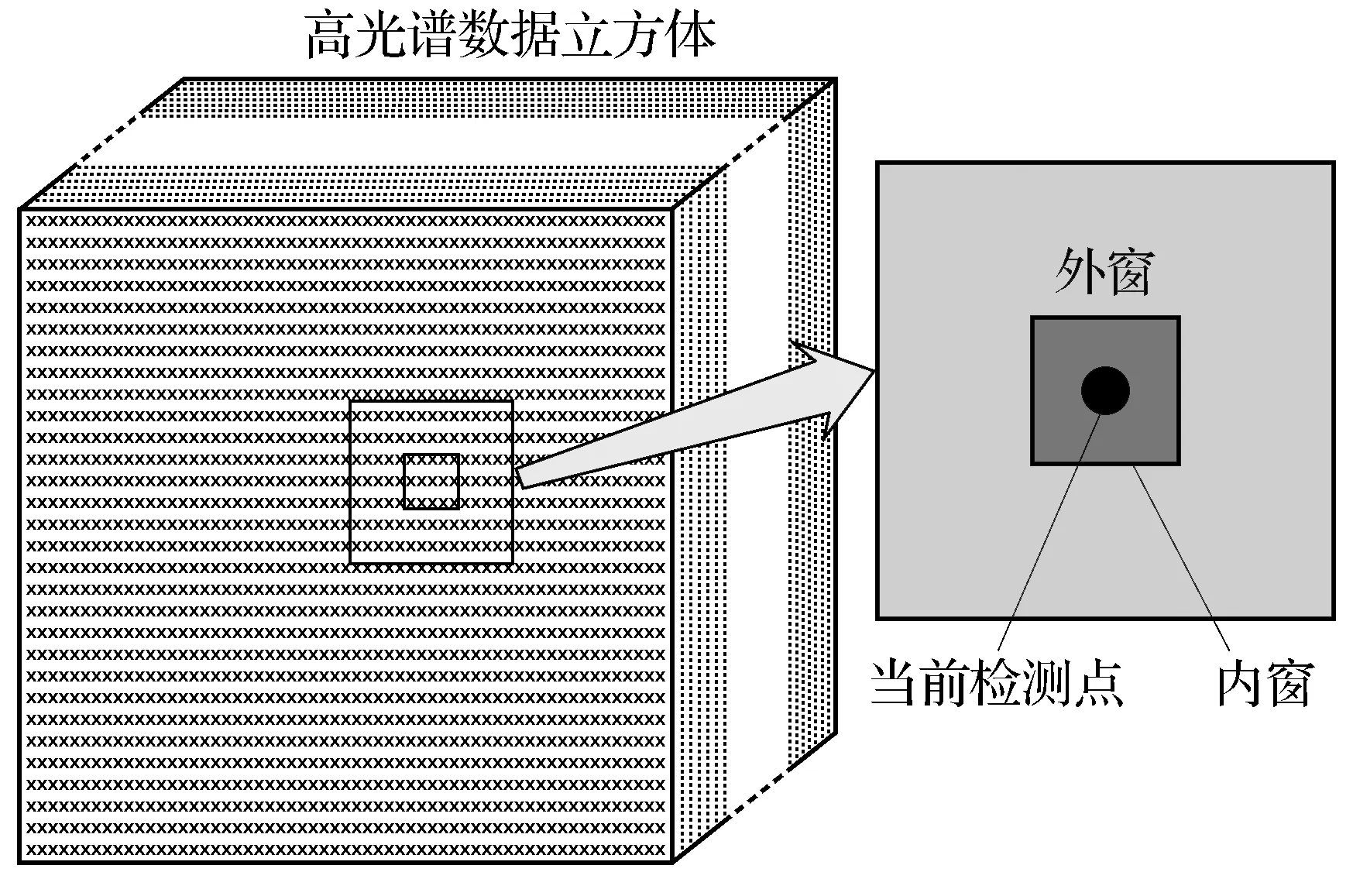
图1 传统的同心双窗口模型Fig.1 Model of traditional dual concentric windows

建立二值假设模型:H0代表目标不存在,H1代表目标存在.xi=[x1i,x2i,…,xMi]T表示一个具有M维波段的高光谱图像第i个样本像元的光谱特性.假设高光谱图像中所含样本像元的总数为N,则其可以表示成一个大小为M×N的背景矩阵Xb,Xb=[x1,x2,…,xN],每一个样本像元均为一个M维列向量.RX算法的二值假设模型如下:

式中:x为一个M×1维的待测样本像元的光谱向量,a=[a1,a2,…,aM]T表示信号光谱向量的丰度,s=[s1,s2,…,sM]T表示目标信号的光谱向量,n表示背景中所含的噪声向量.由式(1)可知,a=0时,H0成立,a>0时,H1成立.假定两种情况下图像中的数据样本像元分别服从N(μb,Cb)和N(μs,Cb)的多维高斯分布.其中μb和μs分别为局部窗中背景和目标的均值,Cb为局部窗中样本像元的协方差矩阵.

通过广义似然比检验及一系列化简,得到的RX算法的判决表达式为

其中,η为表达式的判决门限值.Chang等人在此基础上,对RX算法进行了改进,提出了基于样本自相关矩阵的RX算法[11],它的简化形式如下:

2 基于逐行处理的RX异常检测算法

传统的基于局部检测的RX算法是以待测样本像元为中心内外嵌套的双窗口模型,算法执行时需要对复杂矩阵进行大量的求逆运算,增加了算法的运算时间,导致算法时效性较差.为降低算法的计算复杂度,实现逐行架构中对异常目标的快速检测,本文提出一种局部半窗模型,在逐行获取数据流的同时通过局部半窗的滑动来完成图像中背景信息的有效更新.

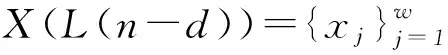
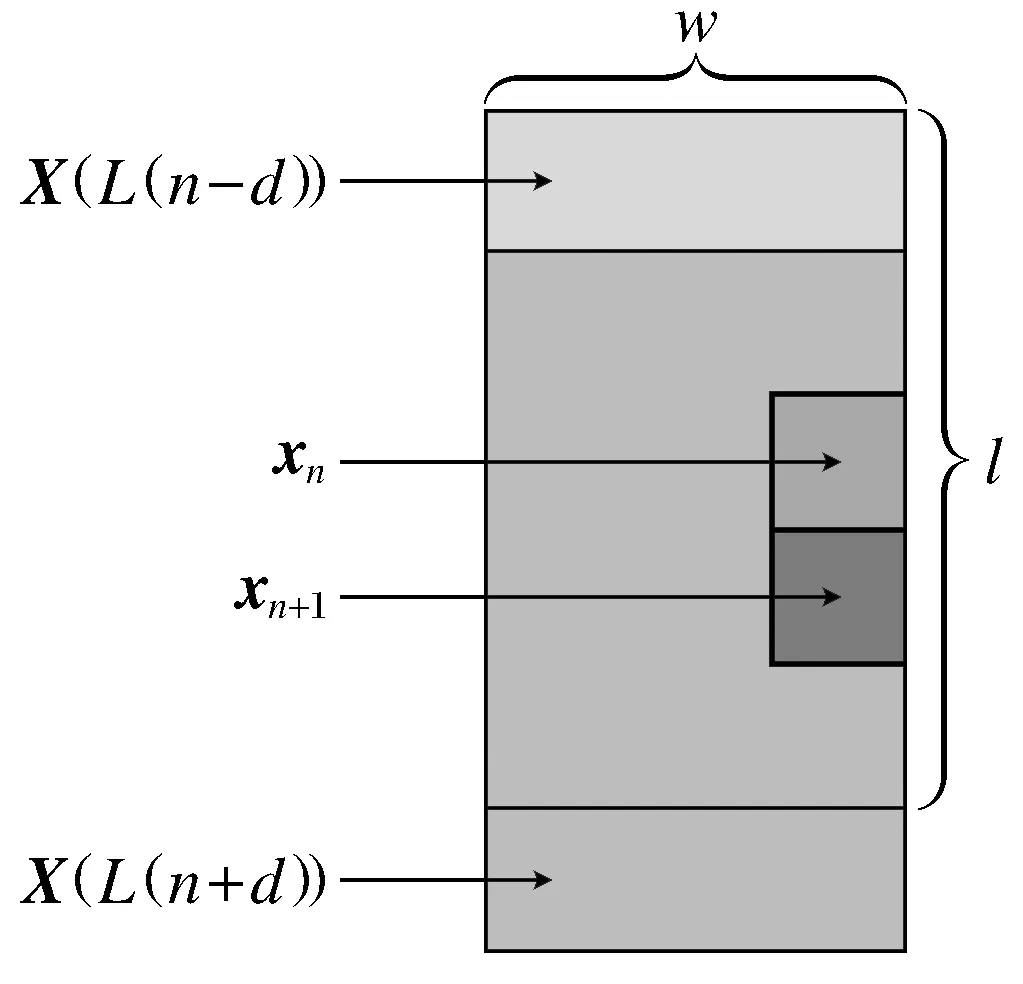
图2 xn和xn+1为中心的局部半窗Fig.2 Local semi-windowsmodel atxnandxn+1

将基于滑动窗模型的RX算法表示为

式中:W为当前检测窗;xn为当前检测窗中待测样本像元;RW(n)为当前局部窗中样本像元的自相关矩阵.式(7)虽然能够实现基于逐行处理架构的高光谱异常目标检测,但需要对局部自相关矩阵RW(n)进行大量重复的矩阵求逆运算,降低了算法的运算效率,因此需要对RW(n)的逆矩阵进行递归更新.假设xn为上一时刻滑动窗中待测样本像元,则当前检测窗中的待测样本像元为xn+1时,则可以将式(8)表示为

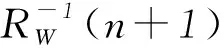
将式(9)中的前两项作为一个整体,记为式(11):

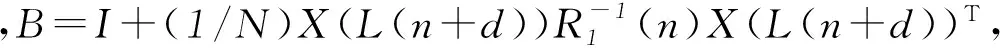
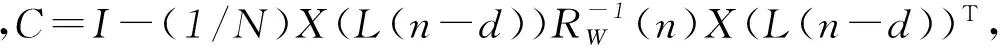
利用BLRXD算法计算样本的RW(n)时,需要计算初始样本的RW(n)initial,此时滑动窗口尺寸的选择尤为重要.窗口尺寸选择过大,将破坏局部高斯假设模型,窗口尺寸选择过小将无法保证RW(n)均为满秩矩阵,因此为了避免出现奇异矩阵,应使滑动窗口中包含的样本像元的个数大于样本像元的维数(通常情况下为保证可靠估计,一般令N≈5·M)[13].

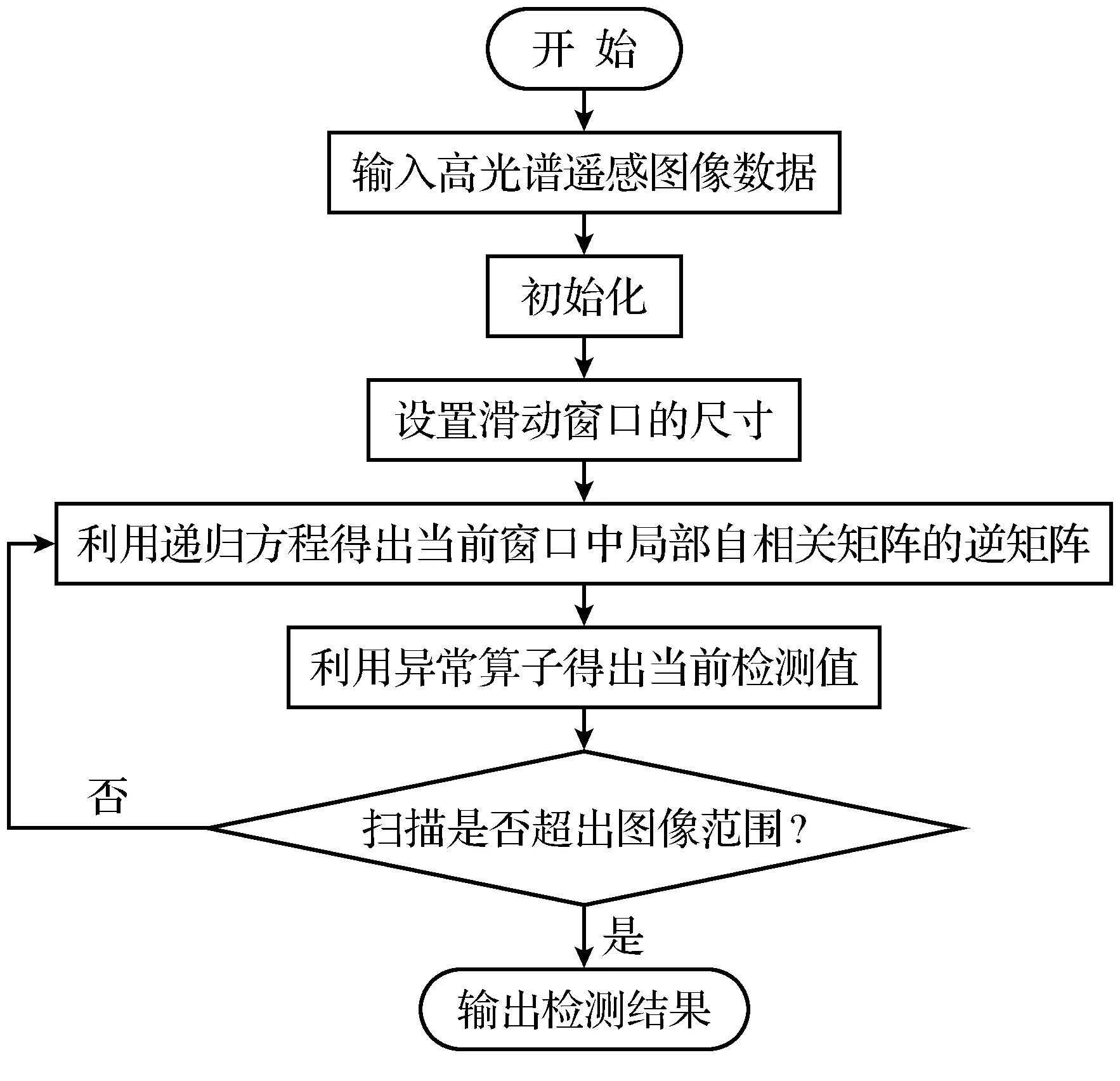
图3 算法流程图Fig.3 Flow chart of the algorithm

为了客观地评价BLRXD算法的时效性,表1对RXD算法和BLRXD算法的复杂度进行了量化分析.因为在算法运行过程中,执行加法操作所耗费的时间可以忽略不计,因此本文仅考虑乘法计算量对两种算法复杂度的影响.可以看出与RXD算法相比,BLRXD算法由于利用了Woodbury矩阵求逆引理,实现了大矩阵的递归更新,避免了复杂矩阵求逆时统计信息的重复计算,使算法的复杂度大大降低.

表1 算法复杂度分析Table 1 The algorithm complexity analysis

3 实验仿真与分析

3.1 高光谱图像数据

为了验证BLRXD算法的有效性和可行性,图4选取一幅由反射光学系统成像光谱仪传感器(Reflective Optics System Imaging Spectrometer sensor, ROSIS)拍摄的真实高光谱图像,实验数据为意大利帕维亚城市中心(PaviaC),来源于巴斯克大学网站上的公开数据.图像大小为115×115,空间分辨率为1.3 m×1.3 m,在0.43～0.86 μm范围内获取图像信息,去除水吸收波段和低信噪比波段后,剩余102个波段用于后续实验.其中桥上的7辆汽车作为待测异常目标(图4).

图4 PaviaC图像数据及真实异常目标分布Fig.4 PaviaC image and distribution of ground objects

实验仿真环境为MATLAB2014a,通过MATLAB编程语言对算法的检测性能进行详尽论证.论文选用的实验操作平台为Intel(R) Core(TM) i7-4770k处理器,主频为3.50 GHz,安装内存(RAM)为16 GB,系统类型为64位操作系统.操作界面如图5所示.

图5 MATLAB操作界面Fig.5 Operation interface of MATLAB

3.2 实验仿真及分析

为了验证BLRXD算法的有效性,在本节,将BLRXD算法与RXD算法和KRXD算法进行实验对比.通过交叉验证,选择大小为a=37,b=17的滑动窗进行实验.由图6可以看出,BLRXD 算法与RXD 算法和KRXD算法的检测效果基本一

图6 算法检测灰度图Fig.6 Grayscale image of algorithm detection

致.为了进一步验证这三种算法的检测效果,对实验结果做出更加形象化的描述,图7给出了BLRXD算法与RXD算法和KRXD算法的的三维峰度图,可知三种算法均能够很好地检测出异常目标的准确位置,验证了BLRXD算法的有效性.

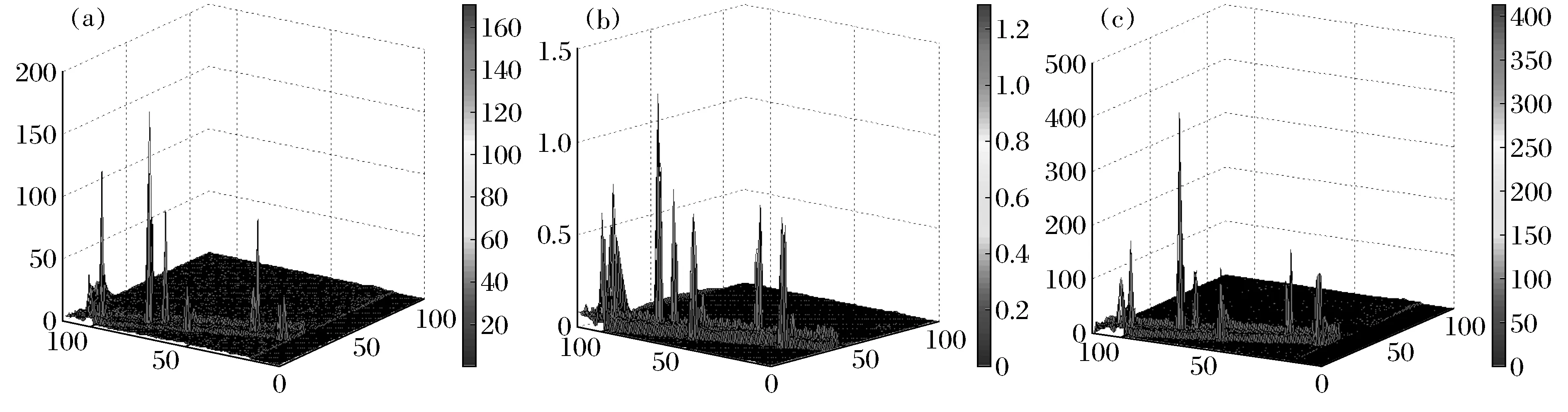
图7 算法检测三维峰度图Fig.7 3D kurtosis image of algorithm detection

接收机工作特性曲线(Receiver Operating Characteristic,ROC)是衡量算法检测性能优劣的评价指标之一.它是在不同阈值下由虚警率pf和检测概率pd构成的关系曲线,提供对算法检测性能的定量分析.其中pf定义为检测到的虚警像素数目Nmiss与图像中总的像素数目Ntotal的比值,pd定义为检测到的真实目标数目Nhit与图像中总的真实目标数目Ntarget的比值.

pf=Nmiss/Ntotal,pd=Nhit/Ntarget.

(14)

图8为BLRXD算法与RXD算法和KRXD算法的ROC特性比较,可以看出,由于所选高光谱图像的地物分布较为简单,三种算法的检测性能比较相近.但由于KRXD算法充分利用了高光谱波段间的非线性光谱特性,其所获得的检测效果要更优一些.在虚警率不大于0.2%时,三者的ROC曲线基本重合,说明对于虚警率要求较高的情况,BLRXD算法有着更好的适用性.

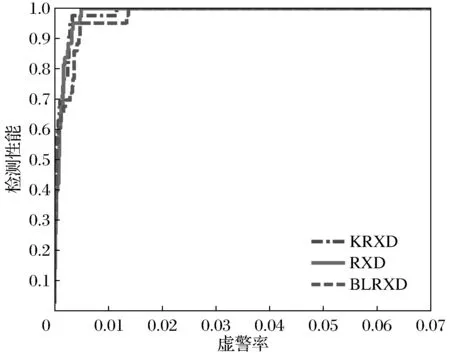
图8 ROC性能曲线分析图Fig.8 Analysis diagram of ROC performance curve

为了验证本文所提算法在时效性方面的优势,表2对未进行递归更新的RXD算法、进行递归更新的BLRXD算法和KRXD算法总的运行时间进行了分析讨论.可以看出,与RXD算法和KRXD算法相比,BLRXD算法由于在算法执行过程中利用Woodbury引理对复杂矩阵的逆矩阵进行递归更新,运行时间明显减少,运算速度有明显优势,与RXD算法相比,其加速比为6.6倍,而与KRXD算法相比,其加速比可达28倍.

表2 算法运行时间Table 2 Computing time of algorithm

4 结 论

RX异常检测算法在高光谱异常目标检测领域得到了广泛关注,本文在高光谱逐行成像的基础上,提出了一种基于逐行处理的高光谱异常目标快速检测算法.该方法利用局部半窗的滑动完成异常目标的检测识别,引入卡尔曼滤波器的递归思想和Woodbury矩阵引理,实现了大矩阵的递归更新,避免了矩阵求逆的高维度计算.通过对算法复杂度的量化分析,验证了该方法在时效性上的优越性.实验结果表明,本文算法在保持检测精度基本不变的前提下,具有更快的运算速度,实用性更好.

[1] TITS L,SOMERS B,COPPIN P. The potential and limitations of a clustering approach for the improved efficiency of multiple endmember spectral mixture analysis in plant production system monitoring[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012,50(6):2273-2286.

[2] 谭克龙,万余庆,杨一德,等. 高光谱遥感考古探索研究[J]. 红外与毫米波学报, 2005,24(6):437-440. (TAN K L,WAN Y Q,YANG Y D,et al. Study of hyperspectral remote sensing for archaeology[J]. Journal of Infrared and Millimeter Waves, 2005,24(6):437-440.)

[3] DATT B,MCVICAR T R,Van NIEL T G,et al. Preprocessing eo-1 Hyperion hyperspectral data to support the application of agricultural indexes[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003,41(6):1246-1259.

[4] 李志忠,杨日红,党福星,等. 高光谱遥感卫星技术及其地质应用[J]. 地质通报, 2009,28(2) :270-277. (LI Z Z,YANG R H,DANG F X,et al. The hyperspectral remote sensing technology and its application[J]. Geological Bulletin of China, 2009,28(2):270-277.)

[5] 赵春晖,孟美玲,李威. 基于子空间异常增殖字典的高光谱图像目标检测算法[J]. 沈阳大学学报(自然科学版), 2016,28(1):33-40. (ZHAO C H,MEI M L,LI W. Hyperspectral imagery target detection algorithm based on subspace outlier proliferation dictionary sparse representation[J]. Journal of Shenyang University(Natural Science), 2016,28(1):33-40.)

[6] SCHAUM A. Spectral subspace matched filtering[J]. Proceedings of the SPIE-The International Society for Optical Engineering, 2001,4381:1-17.

[7] CHANG C I,WANG S. Constrained band selection for hyperspectral imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006,44(6):1575-1585.

[8] REED I S,YU X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1990,38(10):1760-1770.

[9] 赵春晖,王鑫鹏,姚淅峰. 基于近似目标后验信息的高光谱异常检测[J]. 沈阳大学学报(自然科学版), 2016,28(3):212-218. (ZHAO C H,WANG X P,YAO X F. Hyperspectral anomaly detection based on posterior information of approximate target[J]. Journal of Shenyang Universiy(Natural Science), 2016,28(3):212-218.)

[10] ROSSI A,ACITO N,DIANI M,et al. RX architectures for real-time anomaly detection in hyperspectral images[J]. Journal of Real-Time Image Processing, 2014,9(3):503-517.

[11] CHANG C I,CHIANG S S. Anomaly detection and classification for hyperspectral imagery[J]. IEEE Transaction on Geoscience and Remote Sensing, 2002,40(2):1314-1325.

[12] 张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004. (ZHANG X D. Matrix analysis and applications[M]. Beijing: Tsinghua University Press, 2004.)

[13] RICHARDS J A. Remote sensing digital image analysis[M]. New York: Springer, 1993.

【责任编辑: 李 艳】

Hyperspectral Anomaly Detection Algorithm by Using Recursive Polynomial Function

ZhaoChunhui,DengWeiwei

(College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China)

The ever-expending hyperspectral dataset has brought tremendous pressure to the hyperspectral anomaly detection. Accordingly a progressive line processing of RX which can perform RX for anomaly detection progressively line by line by using recursive polynomial function is presented. The thought of Kalman filter and Woodbury’s lemma are used to avoid repeat computation of high-dimensional data matrices. Experimental results show that the accuracy of anomaly detection is guaranteed and testing time of the algorithm is reduced at the same time when compared with the traditional RX algorithm.

hyperspectral image; anomaly detection; line-by-line processing; local window

2016-07-07

国家自然科学基金资助项目(61405041,61571145); 黑龙江省自然科学基金重点项目(ZD201216);哈尔滨市优秀学科带头人基金资助项目(RC2013XK009003).

赵春晖(1965-),男,黑龙江汤原人,哈尔滨工程大学教授,博士生导师.

2095-5456(2017)01-0026-06

TP 751.1

A