城市复杂动态交通路网模型与拥塞分析
王 丹, 李佳洋, 李蓓蕾(沈阳大学 . 装备制造综合自动化重点实验室, . 信息工程学院, 辽宁 沈阳 110044)
城市复杂动态交通路网模型与拥塞分析
王 丹a, 李佳洋b, 李蓓蕾a
(沈阳大学 a. 装备制造综合自动化重点实验室, b. 信息工程学院, 辽宁 沈阳 110044)
将整个交通路网作为一个复杂系统进行研究,关注个体之间的相互作用.综合考虑了人流量和车流量以及不确定的天气情况信息对整个交通路网的影响.进一步确定这些因素对整个路网所带来的负面影响.用数值仿真分析的方法对路网模型进行分析,以判断这些不确定性因素与交通拥塞之间的关系.
交通路网模型; 拥塞; 复杂网络
作为智能交通系统中的核心问题,城市交通拥塞控制问题愈来愈受到关注.解释交通现象、分析交通问题及指导和规范交通管理的研究基础是交通路网模型.研究路网结构的变化对交通路网所产生的费用、流量及拥塞的变化,利用这些运行规律,可以提高交通路网的吞吐量.同时通过这些研究,还可以反推城市交通路网演化机理,摸清运行规律,从而为城市交通规划、控制和管理提供决策依据.当前最有效、最根本的途径是通过信息、控制技术来提高和完善交通控制和管理的能力,进一步提高交通运输效率[1].
国内外的学者关于交通网络模型的研究有很多[2-9].“存储与向前”模型[5]是一个由Gazis提出的带有连续数学描述的简单模型,但它仅用于饱和交通时的状况.之后由Barisone[6]提出后经过由Dotoli发展的模型[7]将一些实际要素考虑进去,不足之处在于该模型含变量过多,很难从实际交通环境中采集到.最近由Berg[9]在Kashani[8]提出的模型基础上进行了改进,使得该模型在不确定的交通状况下能够使用(可能有不饱和,饱和与过饱和),且计算简单,变量较易获取.但是实际环境中车辆排队的时间也需要考虑进去,而这也正是此模型的缺陷,还需深入研究.
城市空间结构的复杂性,各个节点、路段交通量的实际状况和一些不可预知的非确定因素都会影响交通的整体通行情况.城市交通拥堵问题是如何产生的,国内外学者有着不同的见解.学者安东尼·唐斯认为交通拥堵产生的原因有三个[10]:首要原因是上下班时间段出现人流高峰期的概率非常高;其次可归为人口的飞速增长;三是多发的意外事故,例如道路状况、恶劣天气等都极有可能造成路段拥塞的现象.有些学者对交通拥堵产生的根源[11]进行了深入的研究,发现交通瓶颈是制约城市交通的关键因素.依据形成原因,交通瓶颈可以分为两类.第一类是随机事件引起的交通瓶颈:特别是在城市相对繁华的主干道,例如大型的商业活动、道路安全或质量的维护、突发的交通意外、社会治安问题等,这些随机事件一旦发生,有可能将拥塞从局部路段扩展到其他次级道路中,如不及时控制和疏导,就会形成交通瓶颈.第二类交通拥堵是由特殊事件引起的,如公路养护、大型活动、突发交通事故、车辆故障、气象灾害等.这些事件随机发生,且持续时间长,如果不能被及时疏导,很可能会发生局部交通拥塞,继续扩散将会引发道路相继故障的产生,最终导致大部分路段的交通瘫痪.第二类交通拥堵是由于网络本身通行能力有限引起的瓶颈,这是因为道路路况不佳,或道路中出现路障而导致的道路变窄而造成行驶速度过慢.除了上述两种之外,城市中信号的标示不明确或是没有及时更新也同样会形成拥塞情况.例如在某时段高峰期内特定区域流量明显增多,即出现了超负荷的交通量,这类信息并没有反馈给交通部门或者驾驶员,有可能会加重此路段的超负荷现象.
由此可见,交通拥堵的根本原因在于交通容量与交通需求的不协调.本文提出一种新的路容量模型,将人流量与车流量同时作为影响因子来描述和分析路段的拥堵情况,路段中人流量的停留时间会直接影响车辆在交叉路口的等待时间以及路段中的等待车辆数.以此为模型更能反映在实际拥堵交通流中的真实情况,从而达到较为准确地反映拥堵情况的目的.
1 城市交通拥塞模型
研究城市交通路网时,因其规模相对较大,系统中需要考察的特性很多,为了减少工作的繁复性,建立一个路网的拓扑结构来表征交通路网的特性,从宏观上关注车辆的集体行为,不再仅限于考虑单个车辆的进入、到达、排队,以及消散等现象,提高了计算的效率,路网模型结构简洁明了,准确理解了网络的整体特性.因此建立城市交通路网模型[12]很有必要,内在的拓扑结构特性是建立模型的重点,使用权重值来表征值节点与节点之间的关系,从而形成一个完整的路网络拓扑结构,来分析和研究网络拥塞程度的影响.
1.1 拥塞的定义
目前,国际上认可度较高的对于拥堵的定义是采用通行能力的评价.在设计与规划城市交通路网时的一个重要指标就是可能通行能力.可能通行能力[13]可以定义为在可预测和控制的交通环境下,在一小时内能通过某车道或道路上某断面的最大标准车辆数.可能通行能力并不是道路的基本通行能力,它是根据实际的道路物理信息进行修正而得到的数值,其中对于修正系数的取得并没有统一的规定,使用可通行能力来表征道路疏导交通的能力.
拥塞定义可分为两种情况[13]:①对于路段而言,欧美国家采用的标准是,单就行车速度和时间的关系,如果车辆行驶速度低于某值(如15 km/h)持续5 min以上就被认定为此时该道路为拥塞状态.②对于交叉口而言,拥堵的评价指标一般采用饱和度系数,拥堵发生时,饱和过度,系数均大于1.本文将拥堵的定义仅限于交叉口中,即在交叉路口前等待通行的车辆数大于某个设定值,可认为该路口发生拥堵,如:
式中:q是拥塞的设定值;x(t)为t时刻该交叉路口前等待的车辆数.
1.2 交通拥塞因子
造成交通拥堵的原因有很多,且有很多客观因素.本文以影响路段交通量的因素作为划分不同交通层次的依据,即人流量和车流量.将以人流量为划分依据的交通层次称为第一交通层次,将以车流量为划分依据的交通层次称为第二交通层次.利用层次分析法来确定交通拥堵的客观因素,从而找到了新的影响路网交通拥塞因子.
路网容量分为两种形式[13]:①广义路网容量, 又被称为最大容纳力,是指单位时间内整个路网内所有的道路和交叉口所容纳的最大车辆数;②狭义路网容量, 即在可预测和可控制的交通状况下,在单位时间内通过路网的瓶颈断面的最大标准车辆数.然而路网容量的大小主要取决于两个因素:路长和路宽(并行车道数).即
式中:c为此路网容量;l为路长;w为路宽(也可由并行车道数来表示).
基于第一、第二交通层次的划分,将路网容量的影响因子也相应地划分为第一、第二因子.
第一因子是以人流量为主要影响因素的路周信息,包括这一路段上的公众聚集点,如商业圈、学校、企业所在地等.商业圈大多数存在于中心商务区,这一部分区域往往是拥堵的多发路段,也可称为交通网络的瓶颈区域[14].通常情况下,在工作日时段,商业圈的人流量较少,相反,人流高峰期多发生在节假日时段,并且在此时段期间人流量处于不规则的波动状态,有时候可能会有好几个波峰.学校在学生上学放学时段,会出现早中晚三个人流高峰点,这个节点出现波峰的具体时刻相对较为规律.对于企业所在地而言,则会出现与学校类似的人流高峰点,但这类人潮相较于学校附近的人流来说,更易于疏导和控制.可以看出,路周信息状况的复杂与否直接影响到l,进而作用于c的变化.可以给出用路周信息来修正路长l的方法:
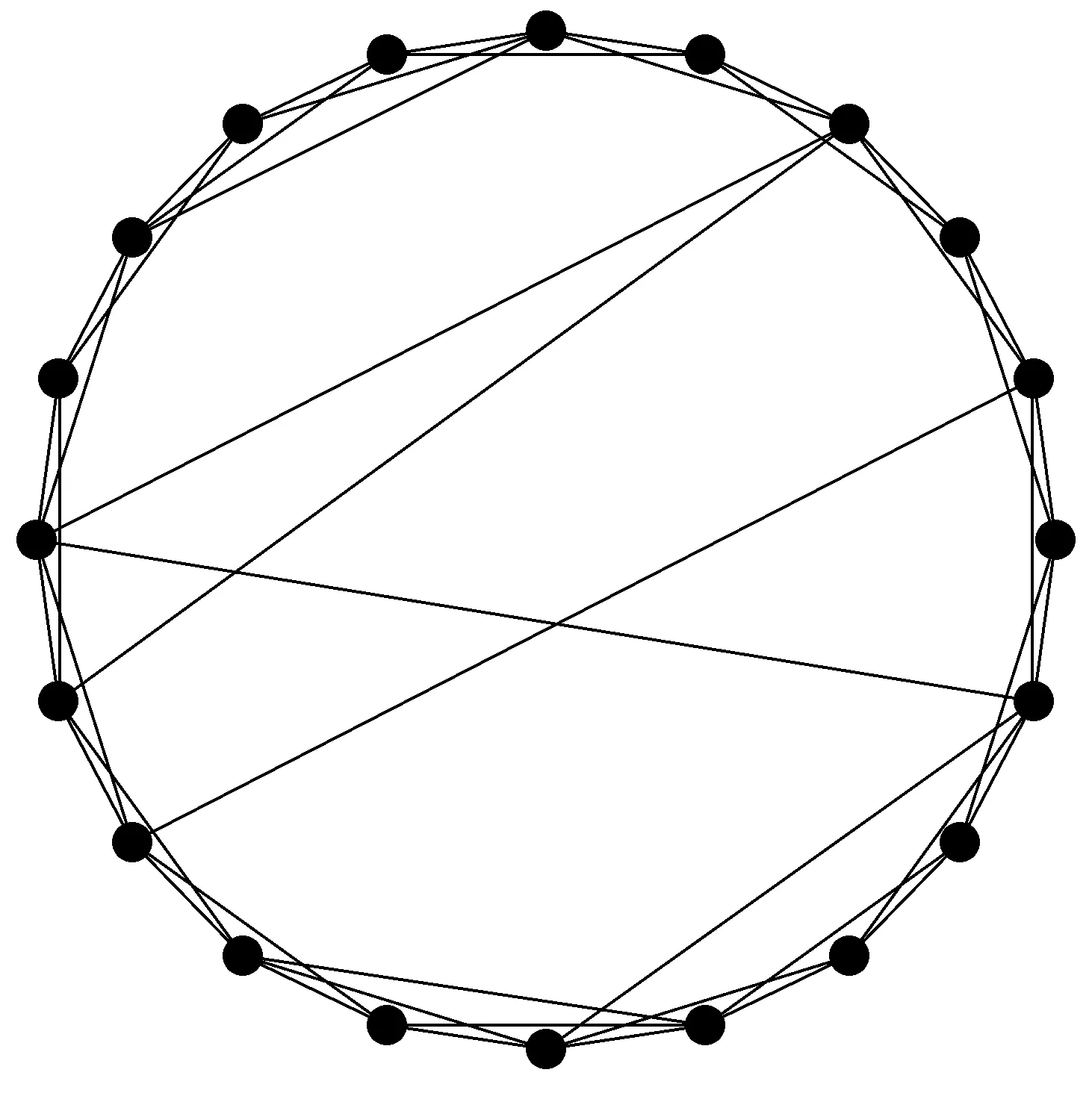
式中,a表示路周信息,如商业圈、学校、企业所在地等的影响,由于其影响强度略有差异,对a的取值可以有不同的系数(0 第二因子则是以车流为主要影响因素的情况.城市交通越来越繁忙,使得人们必须将驾驶速度作为首要安全因素来衡量,因此在各个主要路段或高速路口均会有限速的要求,为了便于研究,可以将限定车速看作一个平均水平.此时,当车流量增大时,就可以认为路长l发生了变化,增加了长度,导致了实际路容量的扩张,很有可能出现完全超出可通行能力的饱和路容量值,即发生了拥堵.基于以上的分析,给出以车流量为变化因子的修正方程. 式中:b1表示车流量增大时的修正系数;b2表示车流量减少时的修正系数. 城市交通网络中包含多个具有不同权值的路段和节点,道路的每个路段根据交通流运动特性的不同又可分为路段合流区域、基本路段和路段分流区域.其中,车辆运行不受分流、合流影响的路段被称为基本路段[15].基本路段特性是目前研究的主要内容,而在城市路段合流区域及路段分流区域方面,大部分都是从静态的路网信息层面作为切入点研究交通流的影响.由于全路网研究的覆盖面较广,区域内局部信息难以被准确捕捉,因此可以将整个路网分解成多个路段容量模型来研究,以单个路段容量模型为基本单位,来映射出整个城市交通路网中的动态交通流信息,从而达到排堵控制的目的[16]. 图1 路段l模型Fig.1 Model of roadl 式中:lr表示实际的路段长度;vl表示车辆行驶速度;tl则表示车辆在此路段的行驶时间.在式(5)中,可以得出vl越小,lr实际值就会越大,也就是说,当车辆行驶速度慢下来的时候,路段上就会积蓄更多的车辆数,这无疑是增加了实际的容量,从另一角度来讲等于是拉长了道路的长度(发生了拥堵). 在这个模型中空闲区域的表达: 但是在实际情况中,车辆排队是需要耗费一定的等待时间的,且在某些时刻或地点这种等待排队时间的权重是比较大的,因此,为了更加有效地反映路网容量的实际值,给出车辆由开始进入该路段到排列到队尾开始等待的这部分时间: 式中:ceil(x)函数表示大于等于x的最小整数;a1l+a2l+…+anl表示所有的路周因素对于路段l的影响总和;b1l+b2l+…+bnl表示当车流量增大或减少时对路段l的影响总和,而pin(t)则表示在t时刻进入到该路段的人流量,特别是在节假日以及上下班高峰期时,整个网络中人流量的比例影响会逐渐增加,在T(t)函数中将会产生较大的影响.其余参数同前文. 通过T(t)函数,可以看出每一辆进入路段l的车辆都可以较为准确地计算出等待排队时间,最先进入路段开始到队尾排队的车辆已经纳入到路段实际载荷量中,因为判断路段是否拥堵的标准之一就是实际的载荷量路段容量的阀值,因此,可以清楚而直观地做出是否拥堵的判断.T(t)的值表明路段的载荷量随车辆等待排队的时间而做正相关的变化.为了便于直观表达,给出在t时刻需要等待的车辆数: 等待排队的车辆数xl(t+1)这一参数更能反映拥堵的严重性,暂且把它当做一个增量,用一个增量函数来和路段容量值这一确定性函数作比较,可以抓住时间的动态变化做边际增减量. 如果xl(t+1)>q,此时可以判断路段l发生拥堵.拥堵系数可表示为 式中:q>0,当0≤cl<0.5时,认为路段l为良性拥堵;当0.5≤cl<0.8时,认为路段l为中度拥堵;当0.8≤cl≤1时,路段l可被认为恶性拥堵,这种拥堵具有级联扩散的效果,当路段l在路网中权值大于0.5时,扩散的效果极为明显且迅速,因此对于此类拥堵,交通部门应提前通知,进行实时疏导,以防造成更大面积的交通瘫痪. 2.1 拥塞程度的矩阵表示方法 将整个交通路网抽象成拓扑结构的矩阵,采用aij=(0,1)表示交通路网中的拓扑结构,整个网络由元素aij组成,其中,aij=1表示第i个道路交叉口和第j个道路交叉口有道路相连接,aij=0表示两个交叉口之间无路段相连接.本文所研究的是基于时变的交通路网模型,因此,假定元素aij在0和1之间变化.为了更好地表现实际交通路网的复杂程度,引入bij(常数)作为网络加权参数来表示网络的耦合程度,耦合程度的变化受到很多未知因素的影响,如人为因素的介入、天气以及道路变化、交叉口路障的影响,都可以在一定程度上影响网络的耦合程度.为了便于研究,设bij=(-1,1),其中,bij=-1表示第i个交叉路口和第j个交叉路口之间存在交通阻塞,此路段的局部拥塞已经产生了负面效果.bij可随时间变化,这里将含有负值的拓扑结构当作一个时变拓扑矩阵,根据矩阵的特征值可知,当bij=-1的数量不断增多时,其最小非零特征值必定会出现负数,当整个网络矩阵中的最小非零特征值出现了小于0的负数时,网络不稳定,鲁棒性较差,会出现网络恶化的可能性. 2.2 数值仿真分析 (1) 图的表示.根据交通路网结构特点,选取NW小世界演化模型作为交通路网仿真模型[17],选取N=20,K=2,p=0.04,该模型正好可以反映交通路网道路特点,一般是1个交叉口有4条道路,与其他相邻的4个交叉口相邻,但高架立交桥的交叉口不仅与相邻的交叉口连接,也可与其他较远的交叉口相连.其网络连接矩阵A表示如下: 图2为20个节点的连接示意图. 图2 节点连接图Fig.2 Node connection diagram (2) 网络拥塞程度分析.L=[lij]20×20是图2的拉普拉斯矩阵,被定义如下的形式: 式中,cij≠0,因为当cij=0,即网络中无拥堵时,网络畅通,不需分析.λmin是矩阵L的最小非零特征值,如果λmin<0,则说明网络不稳定,λmin越小说明网络的拥塞情况越严重.对拥堵道路赋予不同的拥塞系数,对于拥塞系数的赋值结合了上文中的不确定性影响因素,例如:学校在早中晚高峰期时的拥堵状况,商业圈的人流量等,使得赋值更加真实可靠.下面将对图2进行拉普拉斯矩阵分析. (1) 所有节点之间的连接都是“1”无拥堵的情况.这种情况说明交通网络中所有道路都通畅,无拥堵情况,此时通过MATLAB求解特征值发现,其所有特征值都大于等于零,即λi≥0(1≤i≤20),最小非零特征值λmin=0.599 7,说明此时交通网络是稳定的. (2) 当(18,20)和(19,20)之间的拥堵系数为“0.5”的情况.这种情况说明该交通网络中有2条道路出现了中度拥堵状况,通过MATLAB求解特征值发现,最小非零特征值λmin=0.147 7,这说明此时交通网络还是稳定的,但其最小非零特征值明显比无拥堵情况下小很多. (3) 当(1,2)(3,4)(18,20)(19,20)之间的拥堵系数都是“0.5”的情况.这种情况说明该交通网络中有4条道路出现了中度拥堵状况,通过MATLAB求解特征值发现,最小非零特征值λmin=0.027 2,这说明此时交通网络还是稳定的,但其最小非零特征值比2条道路出现中度拥堵情况下小很多,最小非零特征值已接近零,此时的网络系统已接近不稳定状态. (4) 当(1,2)(3,4)之间的拥堵系数为“1”,(18,20)(19,20)为“0.5”的情况.这种情况说明该交通网络中有2条道路出现了严重拥堵,2条道路出现了中度拥堵状况,通过MATLAB求解特征值发现,最小非零特征值λmin=-0.164 5,由于特征值出现了负值,这说明此时交通网络已经不稳定了.这也可以说明,在网络中两条拥堵严重的道路所造成的负面效应远远大于两条拥堵较轻的道路的负面影响,这在实际的交通环境中也是存在的. (5) 当(1,2),(3,4),(18,20),(19,20)之间的拥堵系数为“1”的情况.这种情况说明该交通网络中有4条道路出现了严重拥堵状况,通过MATLAB求解特征值发现,最小非零特征值λmin=-1.276 9,比第4种情况出现的最小非零特征值小了很多,这说明此时网络是非常不稳定的,而且可能爆发相继故障,导致交通网络的整体瘫痪. 以上5组数据说明,同个网络发生拥堵,但拥堵的程度不同,网络稳定性会发生变化,拥堵越严重网络稳定性越差.由于交通网络中的很多情况都是实时动态变化的,包括车流量,交通事故等,导致道路上出现的拥堵情况也是随时变化的.因此通过以上的研究可以为交通管理部门提前预知某个局部交通网络可能出现的严重拥堵提供科学依据,以便提前采取疏导策略,避免产生相继交通瘫痪情况. 本文从拥堵控制的需求出发,利用新的路容量模型对拥堵问题进行描述,采用拉普拉斯矩阵分析网络拥塞程度,研究发现交通网络系统的整体稳定性与单个路网拥堵程度和拥堵数量有一定关系.本文的研究可以深化对城市动态交通流的认识,从而达到加强城市交通网络拥堵控制的目的. [1] 李树彬,吴建军,高自友,等. 基于复杂网络的交通拥堵与传播动力学分析[J]. 物理学报, 2011,60(5):140-148. (LI S B,WU J J,GAO Z Y,et al. The analysis of traffic congestion and dynamic propagation properties based on complex network[J]. Acta Physica Sinica, 2011,60(5):140-148.) [2] 王丹,李蓓蕾. 基于驾驶员流动性偏好的元胞自动机改进模型[J]. 沈阳大学学报(自然科学版), 2015,27(6):457-462. (WANG D,LI B L. Improved model of cellular automata based on driver’s liquidity preference[J]. Journal of Shenyang University (Natural Science), 2015,27(6):457-462.) [3] 王丹,李蓓蕾. 城市复杂动态交通自适应局部路由策略[J]. 沈阳大学学报(自然科学版), 2016,28(3):219-222. (WANG D,LI B L. Adaptive local routing strategy in complex urban dynamical traffic networks[J]. Journal of Shenyang University(Natural Science), 2016,28(3):219-222.) [4] 向郑涛. 基于元胞自动机的交通流建模及实时诱导策略研究[D]. 上海:上海大学, 2013. (XIANG Z T. Traffic flow modeling and real-time induction strategy research based on cellular automata[D]. Shanghai: Shanghai University, 2013.) [5] D’ANA G C,GAZIS D C. Optimal control of oversaturated store-and-forward transportation networks[J]. Transportation Science, 1976,10(1):1-19. [6] BARISONE A,GIGLIO D,MINCIARDI R. A macroscopic traffic model for real-time optimization of signalized urban areas[C]∥Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, USA, 2002:900-903. [7] DOTOLI M,FANTI M P,MELONI C. A signal timing plan formulation for urban traffic control [J]. Control Engineering Practice, 2006,14(11):1297-1311. [8] KASHANI H R,SARIDIS G N. Intelligent control for urban traffic system[J]. Automatica, 1983,19(2):191-197. [9] BERG H M V D,HEGYI A B,SCHUTTER D. A macroscopic traffic flow model for integrated control of freeway and urban traffic networks[C]∥ Proceedings of the 42nd IEEE Conference on Decision and Control, Maui, Hawaii USA, 2003. [10] DOWNS A. Can traffic congestion be cured?[J]. The Washington Post, 2006(4):955- 974. [11] PORTAA S,CRUCITTIB P,LATORA V. The network analysis of urban streets: A dual approach[J]. Physica A: Statistical Mechanics and its Applications, 2006,369(2):853-866. [12] LIN S,XI Y G. An efficient model for urban traffic network control[C]∥Proceedings of the 17th World Congress of International Federation of Automatic Control, Seoul, Korea, 2008. [13] 中华人民共和国公安部. 城市道路交通管理评价指标体系[S]. 2012. (Ministry of Public Security of the People's Republic of China. Urban road traffic management evaluation system[S]. 2012.) [14] CRUCITTI P,LATORA V,PORTA S. Centrality measures in spatial networks of urban streets[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2006,73:036125. [15] 郝媛,徐天东,孙立军. 城市快速路常发性交通拥堵分析[J]. 交通与计算机, 2007,25(2):91-98. (HAO Y,XUE T D,SUN L J. Recurrent traffic congestion analysis on urban expressway[J]. Computer and Communications, 2007,25(2):91-98.) [16] 郝媛,孙立军,徐天东,等. 城市快速路交通拥堵分析及拥堵阈值的确定[J]. 同济大学学报(自然科学版), 2008,36(5):609-614. (HAO Y,SUN L J,XUE T D,et al. Analysis of traffic congestion on urban expressway and congestion threshold identification[J]. Journal of Tongji University (Natural Science), 2008,36(5):609-614.) [17] NEWMAN M E J,WATTS D J. Renormalization group analysis of the small-world network model[J]. Physical Letter A, 1999,263(4/5/6):341-346. 【责任编辑: 李 艳】 Urban Complex Dynamic Traffic Network Model and Simulation Analysis of Congestion WangDana,LiJiayangb,LiBeilia (a. Key Laboratory of Manufacturing Industrial Integrated Automation, b. School of Information Engineering, Shenyang University, Shenyang 110004, China) The whole traffic network is studied as a complex system, focusing on the interaction between individuals. The influence of pedestrian flow, traffic flow and uncertain weather condition information on the whole traffic network is considered synthetically. The negative impact of these factors on the entire road network is confirmed further, to determine the relationship between these uncertainties and traffic congestion. traffic network model; congestion; complex networks 2016-07-19 国家自然科学基金青年基金资助项目(61203152); 辽宁省自然科学基金资助项目(2015020037); 辽宁省教育厅杰出青年学者成长计划资助项目(LJQ2014131); 辽宁省教育厅一般项目资助项目(L2014473). 王 丹(1979-),女,辽宁沈阳人,沈阳大学副教授,博士. 2095-5456(2017)01-0031-06 U 491.2+65 A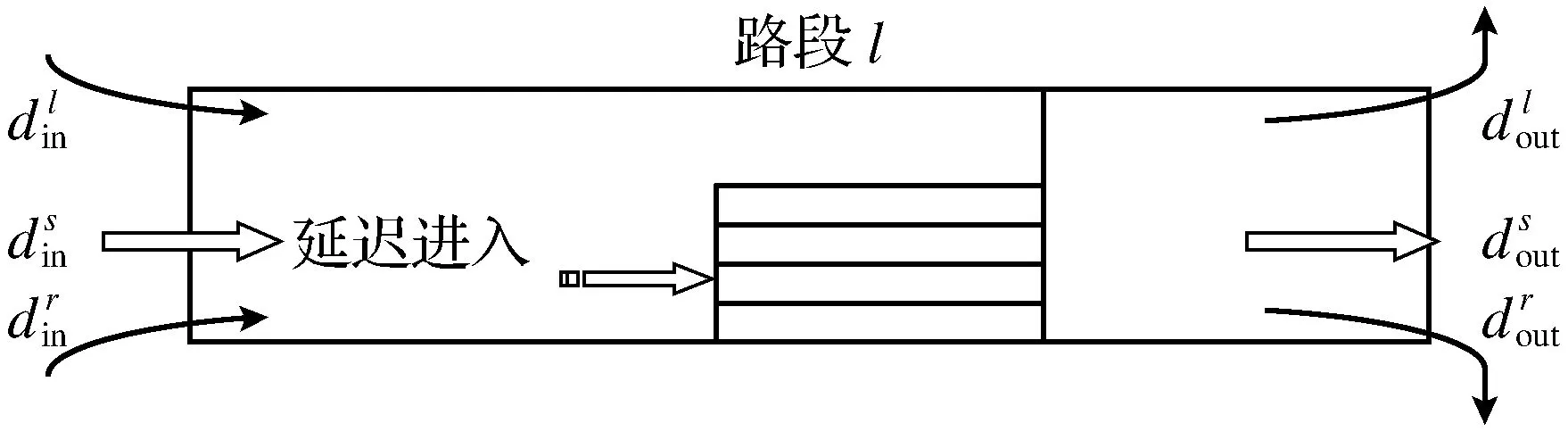
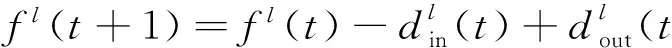
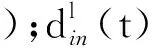
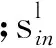
2 拥塞特征分析
3 结 论

