一类含有3n个非零元的谱任意ray模式
张 蓉,高玉斌
(中北大学 理学院,太原 030051)
一类含有3n个非零元的谱任意ray模式
张 蓉,高玉斌
(中北大学 理学院,太原 030051)
若对任意n次首一复系数多项式f(λ),都存在复矩阵A∈Q(P),使得A的特征多项式为f(λ),则称ray模式矩阵P为谱任意的。本文利用幂零-雅克比方法证明了一类含有3n个非零元的n阶ray模式及其母模式为谱任意的。
幂零雅克比;谱任意;符号模式;ray模式
元素取自集合{1,-1,0}的矩阵称为符号模式矩阵,简称符号模式。若A=[aij]是一个实矩阵,则把由aij的符号为元素所组成的矩阵称为A的符号模式,记为sgnA。设为n阶符号模式,记Q(A)={B/B为n阶实矩阵,且sgnB=A},则称为A的定性矩阵类。如果对任意n次首一实系数多项式r(x),在符号模式A的定性矩阵类Q(A)中存在一个矩阵B,使得B的特征多项式fB(x)=r(x),则称A是谱任意的。文献[1]介绍了谱任意符号模式矩阵的定义,并且提出了证明符号模式为谱任意的幂零-雅克比方法。文献[2-4]给出了各种类型的谱任意符号模式矩阵。
若n阶矩阵P中元素为pij∈{eiθ:0≤θ≤2π},则称P为n阶ray模式矩阵,简称ray模式。设p为n阶ray模式,记Q(P)={A=[aij]∈Mn(C):aij=rijpij,rij∈R*,1≤i,j≤n},则Q(P)称为p的定性矩阵类。文献[5]将证明符号模式为谱任意的幂零-雅克比方法推广到了证明ray模式矩阵为谱任意。文献[6]给出了几类含有3n个非零元的n阶谱任意ray模式矩阵。本论文证明了一类含有3n个非零元的n阶谱任意ray模式。
引理1(幂零-雅克比方法) 设A为n阶ray模式矩阵。
1) 在ray模式矩阵A的定性矩阵类中找到幂零矩阵;
2) 用变量t1,t2,…,t2n替换幂零矩阵中eθij的2n个正系数r1,r2,…,r2n,记所得矩阵为x;
3) 矩阵x的特征多项式可表示为:
xn+(f1(t1,t2,…,t2n)+ig1(t1,t2,…,t2n))xn-1+…+(fn(t1,t2,…,t2n)+ign(t1,t2,…,t2n))
若当t1,t2,…,t2n=r1,r2,…,r2n时,雅克比行列式J的值不等于零,则ray模式矩阵A及其母模式都是谱任意的。
本文证明如下含有3n个非零元的n(n≥6)阶ray模式矩阵A为谱任意的。其中2个-1分别在(n,n-m+2)及(n,n)位置上。
设复矩阵B∈Q(A),不妨设复矩阵B有如下形式:
(1)

定理1 设复矩阵B的特征多项式为
令αk=fk+igk,k=1,2,…,n,fk和gk为实系数,则有
(2)
(3)
证明
将行列式第2列的l1=λ倍加到第1列,第j+1列的lj=λj+b1iλj-1+b2iλj-2+…+bji,(j=2,…,n-2)倍加到第一列,第n列的ln-1=(λ-p)ln-2-bnln-m+bn-1i倍加到第1列,使得行列式第1列除(n,1) 位置外,其余都为0。按行列式的第1列展开可得:
所以有

定理2 ray模式矩阵A(n≥6)蕴含幂零。
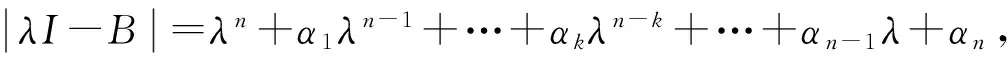



令q→0,则有bj>0,j=1,2,…,n,aj>0,j=1,2,…,m-2,m,…,n,am-1<0。
定理3 ray模式矩阵A(n≥6)为谱任意的。
证明 复矩阵B的雅克比行列式为
[1] DREW J H,JOHNSON C R,OLESKY D D,et al.Spectrally arbitrary patterns[J].Linear Algebra and its Applications,2000,308(1):121-137.
[2] CAVERS M S,VANDER MEULEN KN,Spectrally and inertially arbitrary sign pattern[J].Linear Algebra and its Applications,2005.394:53-72.
[3] CORPUZ L,MCDONALD J J,Spectrally arbitrary zero-nonzero patterns of order 4[J].Linear and Multilinear Algebrs,2007,55(3):249-273.
[4] GAO Y B,SHAO Y L,FAN Y Z.Spectrally arbitrary complex sign pattern Matrices[J].Electronic Journal of Linear Algebra,2009,18:674-692.
[5] MCDONALD J J,STUART J.Spectrally arbitrary ray patterns[J].Linear Algebra and its Applications,2008,429(4):727-734.
[6] GAO Y B,SHAO Y L.New classes of spectrally arbitrary ray patterns[J].Linear Algebra and its Applications,2011,434(10):2140-2148.
(责任编辑 陈 艳)
Class of Spectrally Arbitrary ray Patterns with 3nNonzero Entries
ZHANG Rong, GAO Yu-bin
(School of Science, North University of China,Taiyuan 030051, China)
A ray patternPis spectrally arbitrary if given any monic polynomialf(λ) of ordernwith complex coefficients, and there existsA∈Q(P), thus the characteristic polynomial ofAisf(λ). A class ray pattern of ordernmatrix with nonzero entries was presented.It is show that this ray pattern and its superpattern are spectrally arbitrary by nilpotent-Jacobi method.
nilpotent-Jacobi; spectrally arbitrary;sign pattern;ray pattern
2016-06-28 基金项目:国家自然科学基金资助项目(11071227);山西省回国留学人员科研资助项目(12-070)
张蓉(1991—),女,硕士研究生,主要从事组合数学研究,E-mail:1163064812@qq.com;通讯作者 高玉斌(1962—),男,教授,博士,主要从事组合数学研究。
张蓉,高玉斌.一类含有3n个非零元的谱任意ray模式[J].重庆理工大学学报(自然科学),2017(2):157-162.
format:ZHANG Rong, GAO Yu-bin.Class of Spectrally Arbitrary ray Patterns with 3nNonzero Entries[J].Journal of Chongqing University of Technology(Natural Science),2017(2):157-162.
10.3969/j.issn.1674-8425(z).2017.02.026
O157
A
1674-8425(2017)02-0157-06

