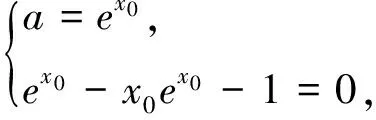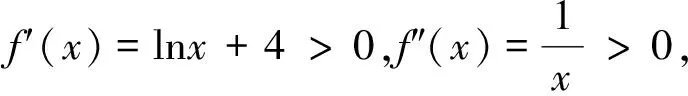利用“切线”处理函数中两类不等式问题
江苏省海门中学 (226100) 吴燕梅
利用“切线”处理函数中两类不等式问题
江苏省海门中学 (226100) 吴燕梅
在高三复习题中,涉及函数与导数的综合问题常常会遇到不等式证明和不等式恒成立求参数范围问题,解题常规方法集中在构造函数求最值或分离参数求范围.但有的疑难问题需要一些技巧,如:虚设零点估算最值,或者分离参数后需要借用高等数学洛必达法则来求最值,而本文以几道例题说明:基于函数凹凸性下尝试构造“切线”来解两类问题.
1.概念与性质
1.1 函数的凹凸性定义
设f(x)为定义在区间I上的函数,若对于I上的任意实数x1,x2和实数λ∈(0,1),总有f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2),则称f(x)为下凸(凸)函数.反之,如果总有f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2),则称f(x)为上凸(凹)函数.
1.2 定理
设f(x)为区间I上的二阶可导函数,则在I上f(x)为凸(凹)函数的充要条件是f″(x)≥0(f″(x)≤0),x∈I.
1.3 性质1
若函数f(x)是凸函数,则经过其图像上一点(x0,f(x0))的切线满足不等式f(x)≥f′(x0)(x-x0)+f(x0),当且仅当x=x0时不等式取等.
性质2 若函数f(x)是凹函数,则经过其图像上一点(x0,f(x0))的切线满足不等式f(x)≤f′(x0)(x-x0)+f(x0),当且仅当x=x0时不等式取等.(证明略.)
2.策略与方法
2.1 凹凸性下构造“切线”证明函数中不等关系
例1 已知f(x)=lnx,g(x)=ex,其中e是自然对数的底数,求证g(x)-f(x)>2.
证明:因为g′(x)=ex,g″(x)=ex>0,所以g(x)是凸函数,g(x)在x=0处切线为y=x+1,则由上述性质1得ex≥x+1,当且仅当x=0时取等;同理可证f(x)是凹函数,在x=1处切线满足不等关系lnx≤x-1,所以ex≥x+1>x-1≥lnx,又两者取等条件不同,则ex-lnx>2,得证.
点评:上述方法是在两个函数上各取一条切线构造不等关系,利用两条切线之间的位置关系(高低)转化得证.
例2 已知函数f(x)=ex-ln(x+m).
(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(2)当m≤2时,证明f(x)>0.(2013年全国新课标Ⅱ理21题)
解:(1)略.
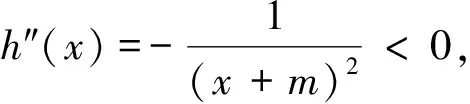
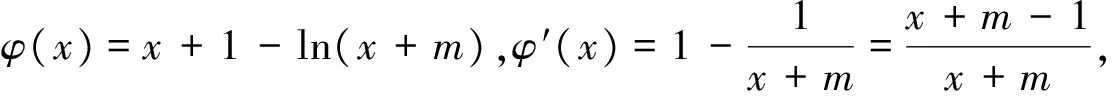
反思:若证形如不等式f(x)-g(x)>0,其中只有一个函数具有凹凸性,可尝试上述方法:假如f(x)为凸函数,可先构造切线证得f(x)≥f′(x0)(x-x0)+f(x0),再证f′(x0)(x-x0)+f(x0)≥g(x)成立,检验等号成立的条件.

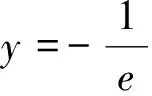
2.2 基于凹凸性巧用“切线”解不等式恒成立求参数范围问题
例4 已知函数f(x)=x(ex-1)-ax2,当x≥0时,f(x)≥0恒成立,求实数a的取值范围.
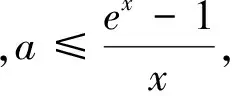
解法2:(直接研究函数最值)x≥0,f(x)≥0等价于x≥0时,ex-1-ax≥0恒成立.令h(x)=ex-1-ax,因为h′(x)=ex-a,(ⅰ)若a≤0时,h′(x)>0,即h(x)在[0,+∞)上单调递增,故h(x)≥h(0)=0成立;(ⅱ)若a>0时,令h′(x)=0,则x=lna.①当lna≤0⟺0 点评:函数的凹凸性为构造切线带来可能,利用数形结合可以方便找到参数的临界值进而确定取值范围,也能打破对常规方法的思维定势,触碰新的解题灵感. 例5 设k∈Z,当x>1时,不等式k(x-1) 解法1:分离参数法(虚设零点求最值,估算k的范围). 解法2:构造函数h(x)=xlnx+3x-2-k(x-1),讨论确定函数的最小值h(x)min>0,求k的范围. 由此可见,借用构造“切线”为处理函数中不等式证明以及求解恒成立时参数范围问题,提供了一种新的“视角”,当然这样的函数需要考察其“凹凸性”,利用数形结合的思想来分析问题.函数与导数的综合问题一直是高考的热点,而不等式的相关问题也是全国卷的常考题型,对于“她”的动向研究是值得的也是有“意义”的事.