一道常见试题变式的再思考
2017-03-16 08:41江苏省盱眙中学211700
中学数学研究(江西) 2017年2期
江苏省盱眙中学 (211700) 梁 义
一道常见试题变式的再思考
江苏省盱眙中学 (211700) 梁 义
波利亚指出:"掌握数学就是善于解题."在实现数学教学目的的过程中,教师应适时的引导学生从不同的方法、角度、思维方式去观察、联想、分析,根据问题的特定条件探索出一系列的解题思路,培养学生的发散思维能力.所以一题多解的教学显得格外重要,它充分让学生自己思维,让学生整理,让学生在探索中发现数学解题的本质,达到触类旁通的效果.
下面笔者通过对一道高中常见试题的变式研究,来加以说明,希望对读者有所帮助.
在教学中给出这题时,学生很自然地给出下面这种做法:

反思:本题中的辅助角虽然不是特殊角,但前面的系数“4,3”都是较为特殊的数,因此对辅助角的取值是可以确定的,所以借助以上方法可以解决.但对于更一般的角,如55°,我们在确定端点值时就显得有点不知所措,这就需要我们结合各种知识,探究更多的解法,以便对这类题达到熟练解决.
方法二:(转化为齐次式)
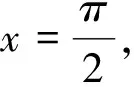

ⅰ)当t=0时,y2=16;
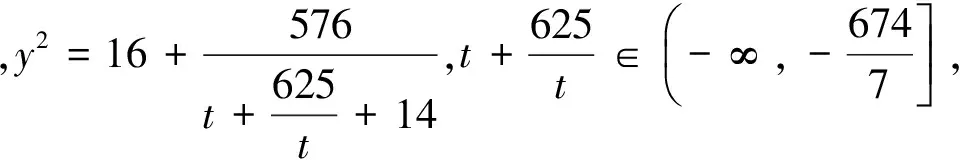
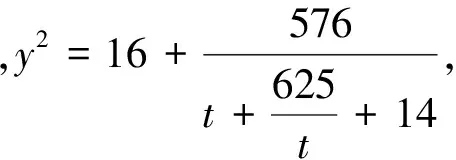
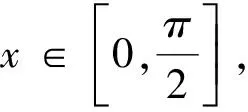
点评:上述方法借助构造齐次式,将问题转化为分式型函数的值域问题,体现了转化的思想,达到了简化的效果!
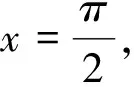
点评:作为求函数值域的强有力的工具,准确地求导,细致地划分单调区间,是解决本题的关键所在.
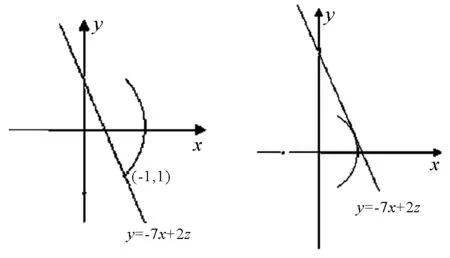
图1
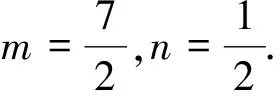
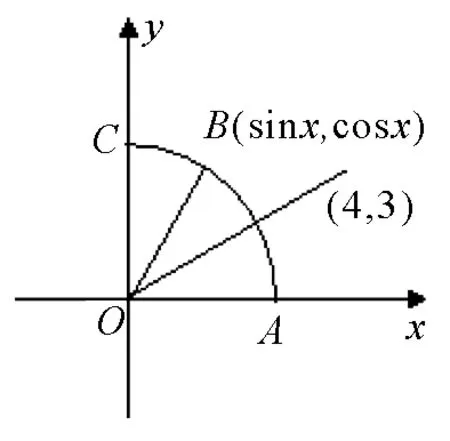
图2
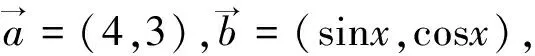
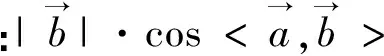
方法六:(点到直线的距离)
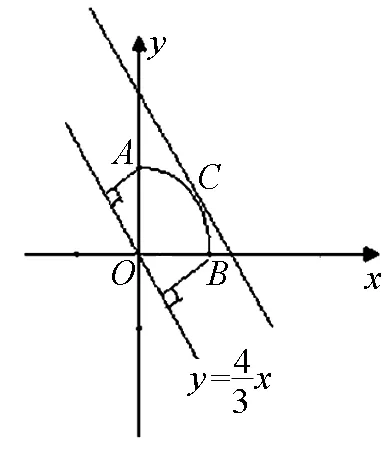
图3
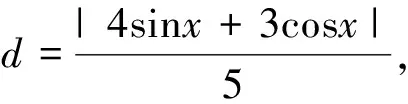
点评:数学家华罗庚曾说过:“数缺形时少直观,形缺数时难入微”,这充分说明了数形结合思想的妙处,正确地建立数与形之间的联系,构建模型,将给我们解题带来更加直观的感受.
猜你喜欢
江苏安全生产(2022年8期)2022-11-01
新世纪智能(数学备考)(2021年9期)2021-11-24
中学生数理化·七年级数学人教版(2020年12期)2021-01-18
新世纪智能(数学备考)(2020年9期)2021-01-04
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27
中学生数理化·高一版(2018年10期)2018-11-08
理科考试研究·高中(2017年10期)2018-03-07
中学生数理化·七年级数学人教版(2017年3期)2018-01-20
求学·理科版(2016年11期)2016-11-29
农产品市场周刊(2014年49期)2015-01-20

