一道习题的另解及推广

江苏省丹阳高级中学 (212300) 史建军

一道习题的另解及推广

江苏省丹阳高级中学 (212300) 史建军

1.问题的提出

引例1 若A为⊙C:(x+5)2+(y+4)2=25上一点，O为原点，OA=2,求直线OA的方程.

2.问题的解法

解法一思路简单，但运算比较复杂；解法二思路、运算均很简洁，但苏教版初中新教材中没有介绍平面几何中的切割线定理，既然是无米之炊，学生只能望洋兴叹.

3.问题的推广

引例2 若A为⊙O:x2+y2=25上一点，P(5,4),且PA=2,求直线PA的方程.

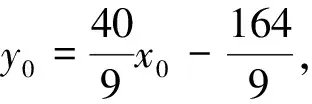
结论3 已知⊙M:x2+y2+Dx+Ey+F=0与直线l:Ax+By+C=0(C≠0)相交于两点，求过交点与P(m,n)的直线方程时，可将⊙M方程变形为(x-m)2+(y-n)2+(D+2m)(x-m) +(E+2n)(y-n)+m(D+m)+n(E+n)+F=0.

结论4 已知二次曲线Ax2+By2+Dx+Ey+F=0与直线l:ax+by+c=0(c≠0)相交于两点，求过交点与P(m,n)的直线方程时，可将曲线方程变形为A(x-m)2+B(y-n)2+(D+2Am)(x-m)+(E+2Bn)(y-n)+m(D+Am)+n(E+Bn)+F=0.直线l方程变形为a(x-m)+b(y-n)+am+bn+c=0,则所求直线方程为A(x-m)2+B(y-n)2+(D+2Am)(x-m)·

证明：一方面，由结论2的证明可知，(4)式经过P(m,n)及两曲线的交点；另一方面，⑷式可化为形如：a′(x-m)2+b′(x-m)(y-n)+c′(y-n)2=0的齐次式，由结论2的证明可知，⑷式可表示为两条直线.

引例3 若⊙C:x2+y2+10x+8y+16=0,直线l:5x+4y+10=0.求过⊙C与直线l的两个交点及原点且对称轴平行于坐标轴的椭圆方程.

根据条件选取参数λ1,λ2的值，可使上述方程表示经过两交点及P(m,n)的直线、圆、椭圆、双曲线和抛物线.