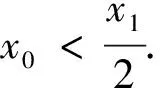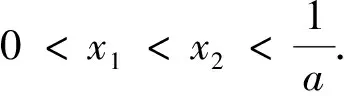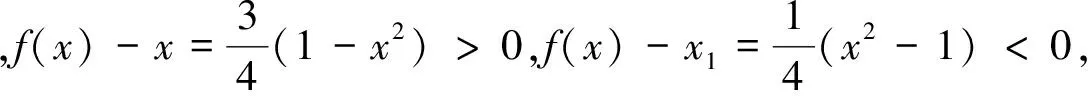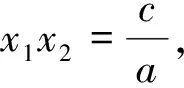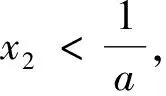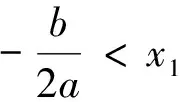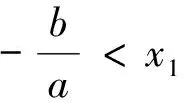变“封闭”为“开放”,让探究更精彩
浙江省绍兴市柯桥区财经学校 (312000) 韩红芳
变“封闭”为“开放”,让探究更精彩
浙江省绍兴市柯桥区财经学校 (312000) 韩红芳
1.问题的提出
近日,笔者担任了学校高三年级数学期中试卷的命题工作.其中,填空题的最后一题系一个高考题的第(Ⅰ)问改变而成.原题是呈现了结论的一个“封闭”题,现设计成一个“开放”型填空题.从阅卷反馈看,学生的得分很不理想.以笔者所任教的两个班(共103人)为例,只有4个学生给出了正确答案是①④,其余学生的答案几乎都是①②.面对这个略显意外的结果,笔者决定利用试卷讲评的机会,花一堂课时间,和学生做一番探究.
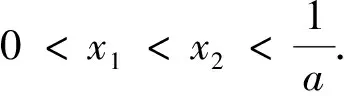
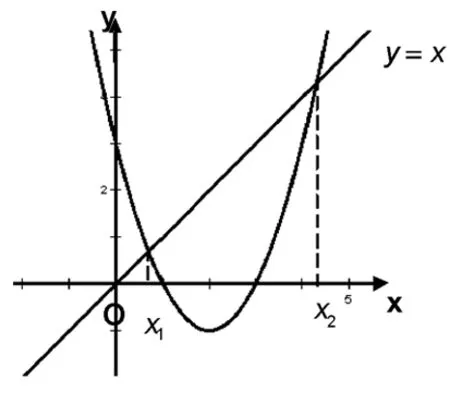
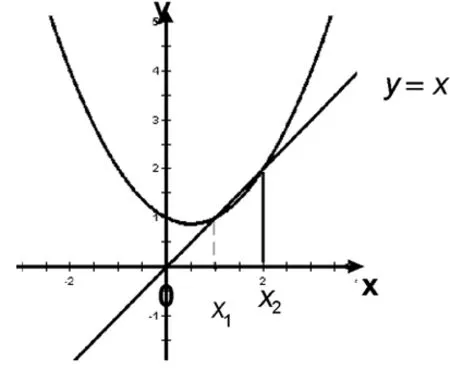
(Ⅰ)当x∈(0,x1)时,证明x 2.探究实录 课堂上,教师先不告诉学生正确的答案,而是请选①②的一位学生来讲讲自己的解法. 图1 生1:采用数形结合的方法.具体是:方程f(x)=x有两根,可转化为抛物线y=f(x)与直线y=x有两个交点,如图1所示.从图形中很容易看出:当0 话音一落,不少学生都附和着说:是这样啊,“秒杀”!见状,教师仍不动声色,只是就学生能运用函数与方程、数形结合的思想方法来解题,表示认同与赞赏.接着, 请选①④的一位学生来谈谈自己的解法. 生2:一开始,我也是这样想的,但发现有个问题: 转而想到解填空题的一个好方法,即用特殊值法来求. 师:很好,面对这两个不同的解法结果,大家怎么看? 经讨论,学生达成下列一致意见:首先,结论①肯定是对的,因为无论直线与抛物线如何相交,在x∈(0,x1)上,抛物线必在直线的上方.其次,借特殊函数检验可知结论②一定错误,即图1是错误的.第三,用特殊函数检验也不能保证结论④一定正确,还需给出一般的推理论证.现先给出结论④的证明. 接下来,学生感兴趣的是:如何正确画出抛物线与直线的位置图形? 图2 由结论f(x) 据此,学生又提出值得证明的两个代数结论: 最后,师生共同归纳:上述填空题的本意是突出考查代数推理与运算能力,编制时基本“堵死”了“借图说话”这条路,即正确图形的得到完全依赖于“以数助形”.因此,在解决与函数有关的问题时,我们要重视几何直观,但也不能过分依赖直观,要把形的直观和数的精密结合起来,才能更深刻、更有效地解决问题. 3.反思 基于上述探究,给我们的启发是: 3.1 变“封闭”为“开放”,让探究更精彩 探究学习能否富有成效地开展,一个很重要的原因是选取适宜的探究问题.而将“封闭题”改为“开放题”,就是一个不错的选择.理由是:面对“封闭题”,学生的状态是“要么会要么不会”;而面对“开放题”,学生的想法就多了,哪怕这些想法不够成熟、甚至是错误的都不重要,重要的是学生的学习会变得更主动、更有趣味,从中提出值得研究和感兴趣的问题也变成可能.总之,将“封闭题”改变为“开放题”,是引导学生展开探究性学习的一个有效举措,值得我们在教学实践中不断尝试、探索与完善. 3.2 让课堂“慢下来”,让讲评更高效 在高三的复习课,特别是试卷讲评课上,很多教师都会采用分析解题思路、讲解解答过程的“教师一言堂”授课模式.这样的课堂容量大、节奏快,看似效率挺高,但实际上学生更多的只是走马观花、疲于应付、浅尝辄止,效果可想而知.日本教育学者佐藤学说过,教育往往要在缓慢的过程中才能沉淀下一些有用的东西.因此,在教学过程中,教师应该让课堂“慢下来”,尊重学生的认知规律,留给学生足够的时间去探究、交流、反思、体悟.唯有如此,学生方能将教师的“外力”真正转化为自己的“内功”,不再发出“老师讲的都能听懂,自己做题还是不会”的感叹. 3.3 代数推理能力应常抓不懈 从填空题测试结果看,学生的确存在一个“软肋”:运算与推理能力较薄弱.原因是:在义务教育阶段,数学教学并没有按照数学的公理化结构组织教学内容,部分定理作为公理使用(教学公理),一些结论(包括定理、公式等)由图形直觉或通过归纳方式就直接确认了.这种处理方式在降低学习难度方面确实非常必要,却也使学生忽略、无视甚至误解了数学推理特征和数学的严谨性要求.同时,义务教育阶段的数学学习也大大降低了数式运算的要求,使得学生的代数式运算能力较低,面对稍稍繁难的运算,有较大的抵触与畏难情绪.所有这一切表明,高中数学一定要特别重视与加强运算与推理能力的培养,就学生而言,一定要让他们明白:学会运算和推理是高中数学学习的两大基本任务,也是今后高考取得好成绩的保证.