三角形截面弹体的跳飞特性研究

章程浩，沈培辉

(南京理工大学 智能弹药国防重点学科实验室，南京 210094)

【装备理论与装备技术】

三角形截面弹体的跳飞特性研究

章程浩，沈培辉

(南京理工大学 智能弹药国防重点学科实验室，南京 210094)

考虑了两种弹-靶极限接触情况对三角形截面弹体临界跳飞特性的影响，对临界跳飞模型进行了数值仿真研究，较好地预测了不同弹-靶接触情况下的临界跳飞特性，解释了不同弹-靶接触情况下接触界面面积大小不同导致弹体具有不同临界跳飞角的主要原因。

爆炸力学；三角形截面；临界跳飞角；数值仿真

斜侵彻倾角足够大时，弹体将在靶板表面直接跳飞，而当倾角略微减小时，弹体则沿着靶板表面形成的弧形弹坑减速跳飞，在弹-靶接触表面形成一个向前移动的接触区[1-2]。在跳飞模型方面，Tate A[3]假设靶板抗力作用于整个弹体，使其产生对弹体质心的转动力矩，Rosenberg Z[4]则假设靶板抗力仅作用于弹体头部位置，两人均建立起了相应的弹体跳飞模型，Woong Lee等[5]通过两者的对比，发现Rosenberg提出的跳飞模型与仿真结果吻合得更好。Johnson W等[6]对不同头部形状弹体的跳飞特性进行了研究，得到了相应的跳飞规律。董玉财等[9]研究了长杆侵彻薄板时的跳飞特性，得到了靶板厚度变化对跳飞特性的影响规律。

我们开展了对三角形截面弹体大倾角斜侵彻靶板的理论研究，建立了两种不同弹-靶接触情况下的临界跳飞角分析模型，分析弹-靶接触情况对临界跳飞角的影响机理。

1 分析模型

1.1 基本假设

弹体的跳飞现象是在弹-靶接触初期发生的，在靶板足够厚的情况下可以忽略靶板边界的影响。为建立三角形截面弹体高速撞击时发生跳飞现象的数学模型，如下基本假设[10]： 1) 靶板有足够的厚度；2) 攻角为0°。

1.2 基本方程

弹-靶碰撞初期的跳弹开坑情况如图1所示。由假设可知，半无限靶板边界条件为无反射边界，不存在应力波在边界的反射造成的影响。

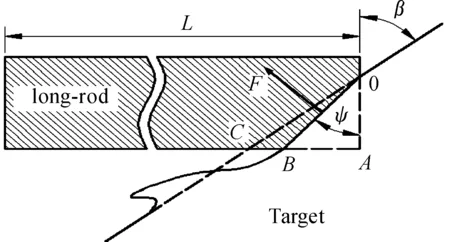
图1 跳弹开坑简化图

此时弹、靶材料处于塑性流动状态，根据修正的伯努利方程，有

(1)

式(1)中，ρp、ρt分别为弹体和靶板的密度，v、u分别为撞击速度和侵彻速度，YP、Yt分别为弹体和靶板的动态屈服强度，Rt为靶板强度，Rt≈3Yt。

当侵彻速度u=0 m/s时，根据式(1)，得到临界速度v′为

(2)

即撞击速度v需大于临界速度v′。

F=SYp

(3)

由图1几何关系可知(v-u)/tanψ=v/tanβ，化简为

(4)

(5)

(6)

受靶板抗力F的作用，杆体将绕质心转动，其运动方程为

Ια=M

(7)

式(7)中，I为三角形截面弹体对过质心横轴的转动惯量，M为抗力F对弹体质心横轴的力矩。M=Fsinψl/2，α为角加速度，有

(8)

图2 弹-靶接触情况

将式(3)、式(5)、式(6)和式(8)代入式(7)，得到弹体角加速度，有

(9)

将式(3)、式(4)、式(5)代入式(9)，并将角加速度α对时间t积分，根据初始条件w|t=0=0，得到不同条件下的角速度w为

(10)

由于弹体获得了绕质心转动的角速度，当因转动产生的弹端线速度在靶面垂直方向的速度分量大于等于弹体轴向速度在靶面垂直方向上的速度分量时，将产生跳飞现象，记临界跳飞角为β，有

(11)

整理上式，得跳飞条件为

(12)

(13)

式(13)中，侵彻速度可由式(1)得到，即

(14)

图3 弹体截面情况

(15)

在图4(b)所示情况下，θ′≤θ≤π/3，有

(16)

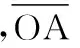
图4 不同θ角时的截面情况

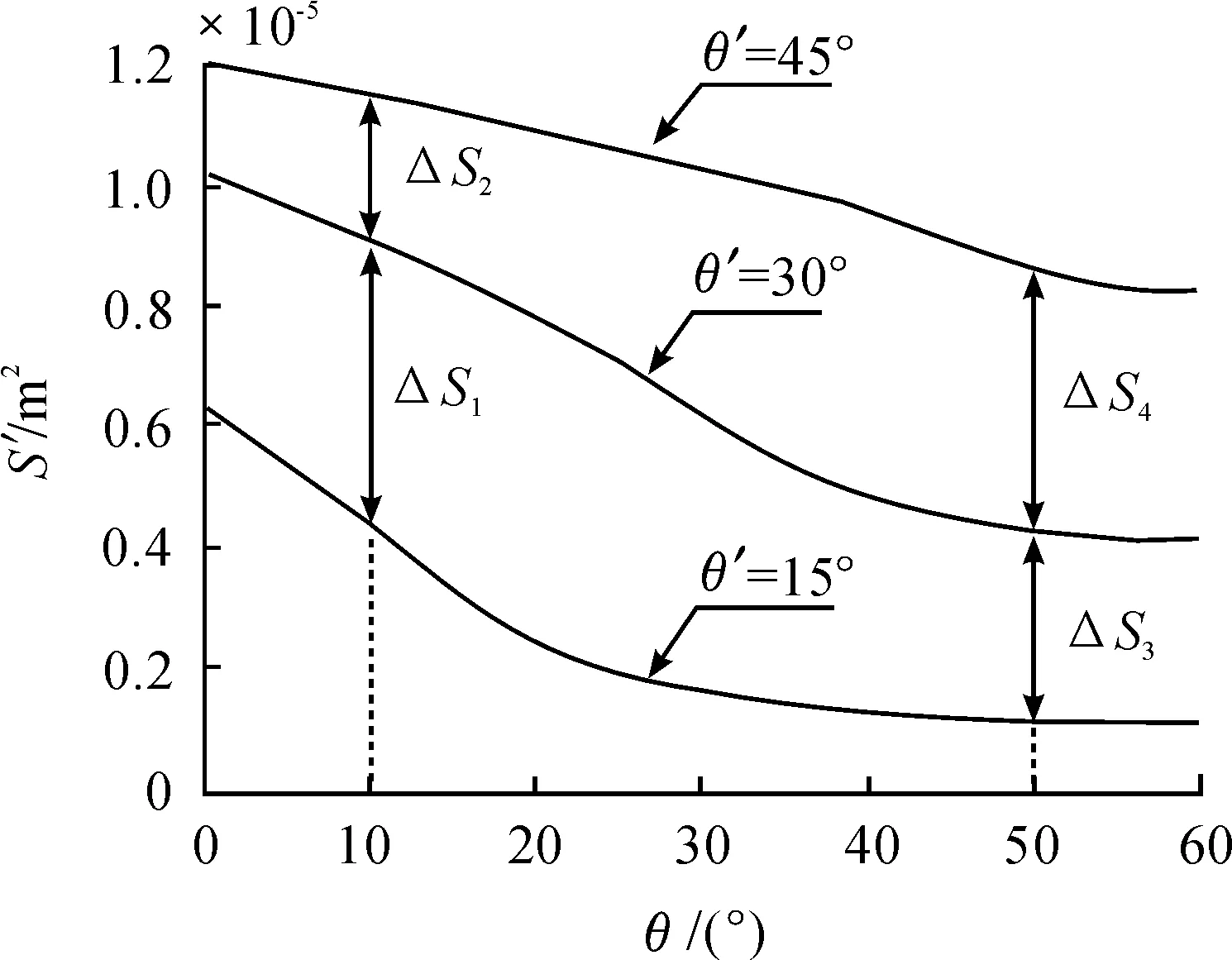
图5 不同θ′时的S′与θ关系曲线

2 数值仿真

2.1 数值计算模型

在1 000～2 000 m/s速度范围内，数值模拟三角形截面93W合金弹体大倾角斜侵彻603装甲钢的跳飞过程。靶板的长、宽分别为250 mm和20 mm，厚度为5 mm。弹体结构及尺寸如图6所示。

图6 弹体结构示意图

弹体和靶板均采用Johnson-Cook材料模型和Gruneisen状态方程。二者间采用侵蚀算法，并与失效准则连用，当单元的有效塑性应变达到失效应变或单元压力达到最小压力时，单元失效，计算中失效的单元将被删除。Gruneisen状态方程的压力表达式为

(17)

式(17)中，ρ0为初始密度，u为内能，μ=ρ/ρ0-1，ρ为当前密度，C、S、γ0和a为材料参数。

Johnson-Cook强度模型的表达式为：

(18)

(19)

式(19)中，Tmelt为材料融化温度，Troom为室温。 弹体和靶板的材料参数如表1所示[11]。

表1 材料参数

2.2 数值仿真结果及分析

调整着靶速度和弹-靶倾角，得到不同着靶速度下弹体的临界跳飞角。

图7为弹-靶线接触时的侵彻情况，着靶速度为1 650 m/s、倾角为86°。从图7(a)中可以看到，受靶板抗力的影响，在t=36 μs时，弹体头部不再与靶板接触，弹体产生了向上的弯曲变形，此时弹体头部尝试恢复水平方向的运动，而弹尾材料依然沿着之前相同的运动轨迹侵入靶板。随着弹体的继续运动，其侵彻情况如图7(b)所示，此时前部弹体沿着靶板表面向前运动，尾部弹体由于继续沿着之前的运动轨迹运动而侵入靶板中，弹坑逐渐变大。由于侵入靶板的弹尾材料受到较大的阻力，而弹体前部仍保持相对较大的运动速度，使得靠近弹坑前部的弹体发生了拉伸变形，弹体截面出现了明显的颈缩现象。如图7(c)所示，在侵彻后期，由于弹体承受了较大的拉力，因而断裂成了一些小段，但靶板在侵彻结束后并未出现通孔。

图8为弹-靶角接触时的侵彻情况，着靶速度和倾角同上。与弹-靶线接触方式不同，在角接触情况下，弹-靶间的接触面积更小，弹体头部在t=36 μs时才不再与靶板接触并向上弯曲变形，这比线接触情况晚了8μs。对比图7(a)和图8(a)可以发现，图7(a)中弹体头部在竖直方向上运动了较大的距离，而图8(a)中的弹体头部在竖直方向上的距离不大，说明弹体头部在弹-靶线接触情况下受到的靶板抗力F更大。随着侵彻的进行，弹体情况如图8(b)所示，弹体此时已完全侵入靶板中，因受到极大的靶板阻力，使得弹体的颈缩现象更为剧烈。此外，相比于图8(b)，图7(b)中只有一半的弹体截面侵彻到靶板中，其受到的阻力更小，因此，弹体的颈缩现象没有图8(b)剧烈。侵彻后期的情况如图8(c)所示，弹尾已穿透靶板并继续运动，靶板出现通孔，头部弹体仍向前运动。

图7 弹-靶线接触的临界跳飞情况

图8 弹-靶角接触的临界跳飞情况

不同弹-靶接触情况下，弹体头部和尾部的水平速度和竖直速度的变化曲线如图9所示。在碰撞靶板之前，弹体头部和尾部的速度相同，水平速度为1 650 m/s，竖直速度为0 m/s。线接触和角接触时的弹体头部速度变化情况分别如图9(a)和图9(c)所示，可以发现，两种接触情况下弹体的水平速度均逐渐减小，竖直方向速度均由零逐渐增大，但线接触情况下弹体的速度变化更为剧烈，其水平速度和竖直速度在更短的时间内便产生了更大幅度的变化。这是由于线接触时弹体头部接触表面受到更大的靶板抗力，使得弹体头部具有更大的角加速度，从而弹体头部速度(尤其是竖直速度)产生了剧烈变化，这与图7(a)和图8(a)中弹体头部在竖直方向上运动距离的变化规律一致。线接触和角接触时的弹体尾部速度变化情况分别如图9(b)和图9(d)所示。由图9(b)中可以发现，对于线接触的情况，在70～90 μs期间，即图7(b)到图7(c)阶段，由于弹体拉伸断裂，弹尾部分材料失去了弹体头部材料向上的拉力，使得弹尾向下运动，此时靶板阻力迅速增大，导致弹尾在70-90μs期间的速度均急速减小，直至减小到0 m/s。同样，对于弹-靶角接触的情况，在图8(b)到图8(c)阶段，弹体发生拉伸断裂，使得弹体向下运动，增大了弹体的阻力，使得水平速度迅速减小，而当尾部弹体穿透靶板后，弹尾的速度大小基本不变，但由于受到不对称的靶板抗力，穿透靶板后的弹体发生了旋转，使得其水平和竖直速度均在94 μs后不断发生小幅变化。

图9 弹体头、尾部的速度变化曲线

改变着靶速度和倾角，进行两种不同接触情况下的跳飞仿真，仿真结果与理论计算结果如图10所示。图10中两曲线之间的区域即为所有弹-靶接触情况下的临界跳飞角区域。在图10中可以看到，线接触情况下的临界跳飞角均小于角接触情况下的临界跳飞角，随着着靶速度的增大，不同接触情况下的临界跳飞角的差值逐渐减小。例如，在理论计算中，两者的临界跳飞角差值在1 050 m/s、1 450 m/s和1 850 m/s时分别为3.52°、1.97°和1.62°，在数值仿真中的差值分别为3.25°、1.25°和1°。此外，通过对理论计算和数值仿真结果的对比可以看到，相同着靶速度下由数值仿真得到的临界跳飞角均大于理论计算值，且随着着靶速度的增大，两者的差值逐渐增大。这是因为，理论分析过程中的临界跳飞角仅考虑了弹体头部的跳飞，而随着弹体长径比的增大，虽然弹体头部向上弯曲变形，但弹尾部分仍然具有向下运动的趋势，因而，理论计算得到的临界跳飞角必定小于数值仿真得到的临界跳飞角。虽然理论与仿真结果存在一定的差异，但该理论模型在整体上与仿真结果具有较好的一致性，说明该模型在该速度范围内可用。

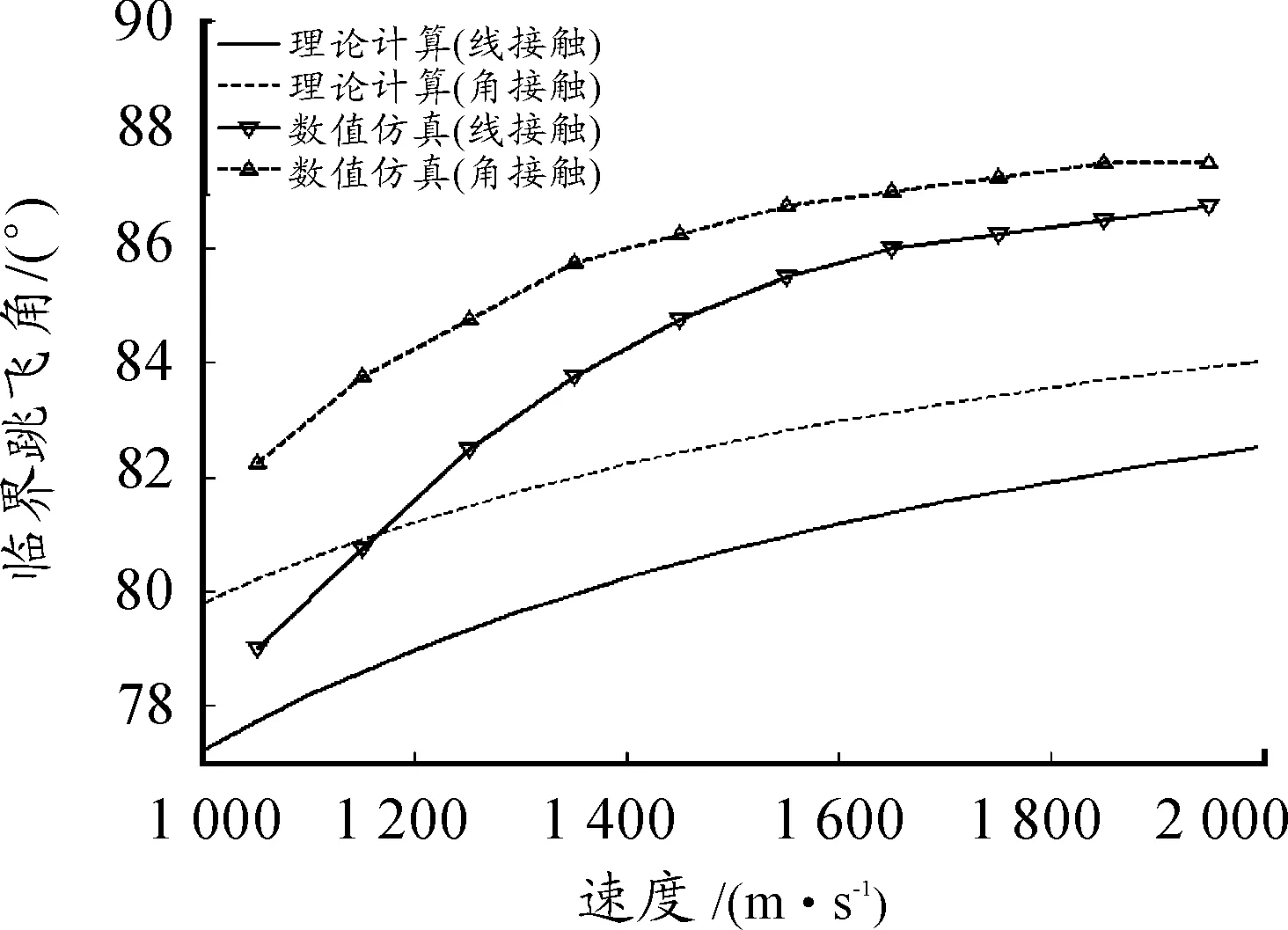
图10 临界跳飞角对比

3 结论

1) 三角形截面弹体大倾角斜侵彻靶板的临界跳飞角模型可以较好地预测不同弹靶接触情况下的临界跳飞特性。

2) 弹靶接触界面面积大小是不同弹靶接触情况下弹体具有不同临界跳飞角的主要原因。

[1] JONAS G H,ZUKAS J A.Mechanics of Penetration:Analysis and Experiment[J].Int J Eng Sci,1978(16):879-903.

[2] ZUKAS J A.High Velocity Impact Dynamics[M].New York:Wiley,1990.

[3] TATE A.A Simple Estimate of the Minimum Target Obliquity Required for the Ricochet of a High Speed Long rod Projectile[J].J Phys D,1979(12):1825-1829.

[4] ROSENBERG Z,YESHURUN Y,MAYSELESS M.On the Ricochet of Long Rod Projectiles[C]//Proceedings of the 11thInternational Symposium on Ballistics.Brussels,Belgium:IBC,1989:942-957.

[5] WOONG L,HEON-JOO L,HYUNHO S.Ricochet of a Tungsten Heavy Alloy Long-rod Projectile From Deformable Steel Plates[J].J Phys D,2002(10):2676-2686.

[6] JOHNOSON W,REID S R.Ricochet of Spheres off Water[J].Journal of Mechanic and Science,1975,17(2):71-81.

[7] SEGLETES S B.A Model for Rod Ricochet[J].Journal of Impact Engineering,2006,32(10):1403-1439.

[8] 胡德安,李霞,梁超.不同头部形状子弹侵彻钢板的跳弹及规律研究[J].应用力学学报,2012(6):752-757.

[9] 董玉财,杜忠华,刘荣忠,等.钨合金长杆体高速撞击薄钢板的跳飞研究[J].弹道学报,2014(1):73-77.

[10]赵国志.穿甲工程动力学[M].北京:兵器工业出版社,1992:121-123.

[11]董玉财,杜忠华,刘荣忠,刘杰.管-杆伸出式侵彻体的威力研究[J].弹道学报,2013(3):50-54.

(责任编辑 周江川)

Research on Ricochet of Projector with Triangular Cross-Section Fragile Projectile

ZHANG Cheng-hao, SHEN Pei-hui

(ZNDY of Ministerial Key Laboratory, Nanjing University of Science and Technology, Nanjing 210094, China)

With triangular cross-section, how the projector-target contact way affect the ricochet characteristics was discussed and the critical ricochet angles theoretical model and is numerical simulation were analyzed. It is able to analyze the ricochet characteristics in different conditions, and to explain that the area size of projector-target contact surface is the main reason to lead to different critical ricochet angles.

explosion mechanics; triangular cross-section; critical ricochet angle; numerical simulation

2016-09-27；

2016-10-31

章程浩(1991—)，男，硕士研究生，主要从事终点效应与目标毁伤研究。

沈培辉(1958—)，男，教授，主要从事终点效应与目标毁伤技术研究。

10.11809/scbgxb2017.02.016

章程浩，沈培辉.三角形截面弹体的跳飞特性研究[J].兵器装备工程学报，2017(2):65-69.

format:ZHANG Cheng-hao, SHEN Pei-hui.Research on Ricochet of Projector with Triangular Cross-Section Fragile Projectile[J].Journal of Ordnance Equipment Engineering,2017(2):65-69.

TJ012.4

A

2096-2304(2017)02-0065-05