全柔性浮筏隔振系统建模与隔振性能分析*

王 真, 赵志高, 刘 芳

(1.武汉纺织大学机械工程与自动化学院 武汉, 430200)(2.武汉第二船舶设计研究所 武汉, 430205)

全柔性浮筏隔振系统建模与隔振性能分析*

王 真1, 赵志高2, 刘 芳1

(1.武汉纺织大学机械工程与自动化学院 武汉, 430200)(2.武汉第二船舶设计研究所 武汉, 430205)

建立了一种包含设备、隔振器、筏架和基础的全柔性浮筏隔振系统的动力学模型。首先,将设备自由振速引入到浮筏隔振系统建模中，提高了模型精度；然后,利用四端参数模型的思想，将筏架的点到点导纳矩阵表示为四端参数网络模型；最后,采用阻抗综合法完成总系统动力学方程，该模型简洁且通用性强。通过数值算例验证了本模型的正确性和有效性，并分别讨论了筏架刚性与柔性以及隔振器参数对隔振效果的影响。所提出的方法对浮筏系统隔振效果的工程计算和设计具有较为重要的理论价值。

浮筏；隔振；柔性；自由振速；四端参数；阻抗综合；振级落差

引 言

大型化、低刚度和柔性化浮筏隔振系统在现代船舶等工程领域得到了广泛应用，浮筏隔振系统的建模与计算是浮筏设计中的重要理论问题。由于筏架的大型化，浮筏和基础的柔性对系统隔振性能有重要影响，同时由于隔振器的大型化，隔振器的固有频率与驻波频率通常较低，因此在浮筏系统建模中，若将筏架或基础视为刚性，将隔振器刚度视为常数，会给浮筏隔振效果的计算带来较大误差。

近年来，有学者围绕柔性浮筏的建模问题开展了研究。文献[1-3]采用四端参数法和模态机械阻抗综合法等子结构分析方法建模，将基础视为柔性体，将筏架作为刚性体。这会导致在高于筏架一阶模态频率时，隔振效果的计算误差较大。文献[4-6]同时考虑了筏架柔性和基础柔性，采用子结构分析法进行柔性浮筏隔振系统的理论建模和隔振性能研究。这些建模方法均是将设备作为刚体，因此模型适用的频率范围受设备一阶模态频率的影响，且需要采用刚柔耦合的方法处理设备与筏架的耦合，增加了建模难度。

从现有的研究工作来看，筏架与设备的处理一直是研究的重点与难点。现有的研究方法通常是利用模态展开法建立筏架模型，这导致建模过程的理论推导复杂。在高于设备一阶固有频率时，将设备视为刚性对于系统隔振效果的计算有较大影响。同时，对于隔振器的处理上，在整个分析的频率范围内将隔振器的动刚度视为常数，这对于隔振系统在高频段隔振效果的计算也会有较大影响。

笔者针对筏架和设备的建模问题，采用四端参数的思想建立筏架和基础模型，并将设备自由振速[7]引入到隔振系统建模中，从而绕开了将设备作为刚体的建模方法。此外，用动刚度表示隔振器的刚度，通过四端参数模型表示隔振器的阻抗特性，利用阻抗综合法建立了包括设备、筏架、基础和隔振器在内的全柔性双层浮筏隔振系统的动力学模型。通过数值算例验证了该模型的正确性和有效性。该模型可以方便地利用实验数据或者是有限元的分析结果建立系统的总体阻抗矩阵，能够快速准确地计算浮筏隔振系统的隔振效果，具有重要的工程应用价值。

1 柔性浮筏隔振系统的动力学建模

将浮筏系统分为设备、上层隔振器、筏架、下层隔振器和基础共5部分，如图1所示。首先，分别对上层隔振器、筏架、下层隔振器和基础建立动力学方程；然后,将筏架上下层隔振系统方程联立，求解设备机脚、筏架上层、筏架下层和基础的振动速度；最后，建立机脚至基础的传递函数模型。

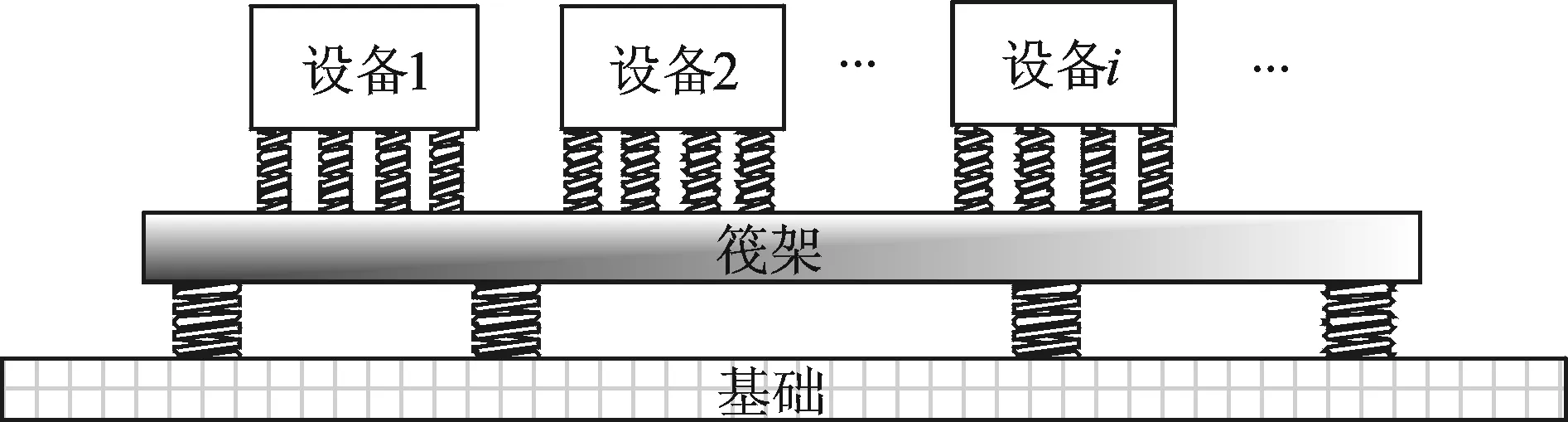
图1 浮筏隔振系统简图Fig.1 Diagram of floating raft system

1.1 设备建模

假设设备为弹性安装条件，其受力如图2所示。

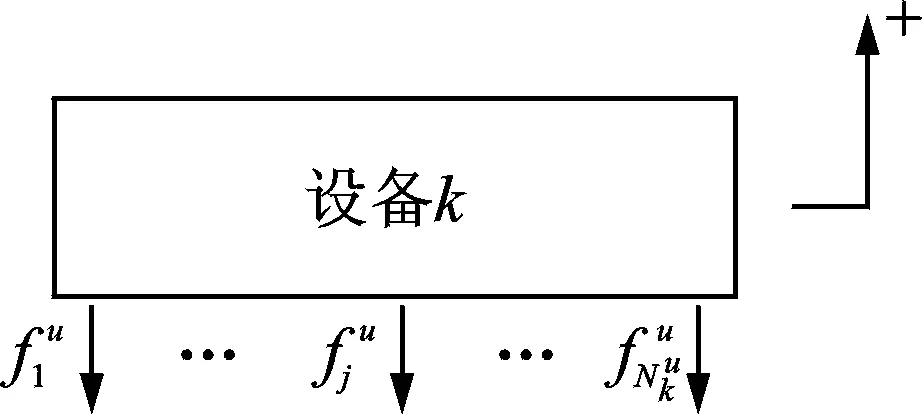
图2 设备受力示意图Fig.2 Load on equipment

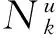
(1)

式(1)表示成矩阵形式为

(2)

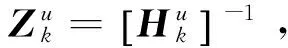
(3)

同理，其他设备机脚的振速也可以表示成式(3)的形式。若筏架上层共有m台设备，则对这m台设备可建立矩阵方程

(4)

1.2 上层隔振器建模

筏架上层隔振器的受力如图3所示。

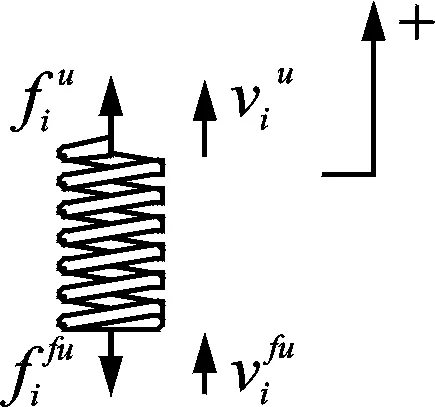
图3 上层隔振器受力示意图Fig.3 Load on upper isolator

根据四端参数描述，第i个上层隔振器的动力学方程为

(5)

式(5)表示成矩阵形式为

(6)

1.3 筏架建模

筏架的受力如图4所示。

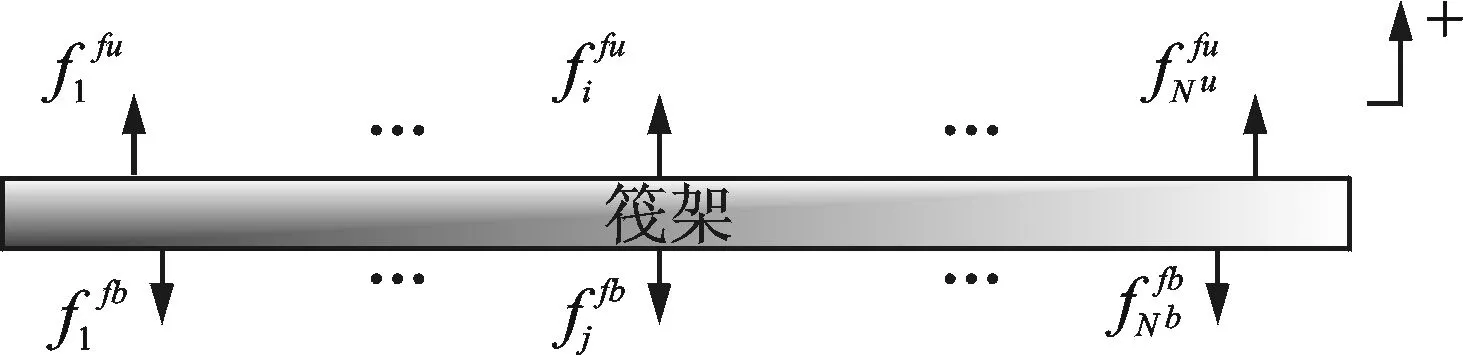
图4 柔性筏架受力示意图Fig.4 Load on flexible raft frame

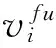
(7)

(8)

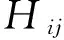
式(7)和式(8)以矩阵形式表示为

(9)

式(9)采用阻抗形式表示为

(10)

1.4 下层隔振器建模

筏架下层隔振器的受力如图5所示。

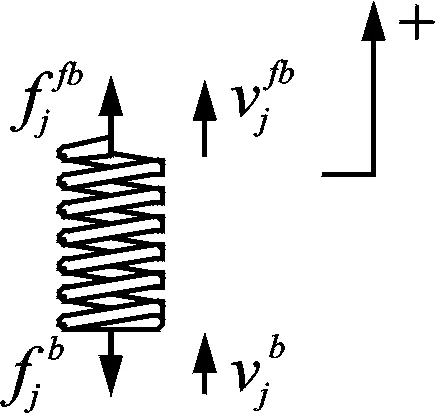
图5 下层隔振器受力示意图Fig.5 Load on lower isolator

根据四端参数描述，与上层隔振器的推导过程相同，下层隔振器的动力学方程写成矩阵形式为

(11)

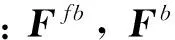
1.5 基础结构建模

基础的其受力如图 6所示。

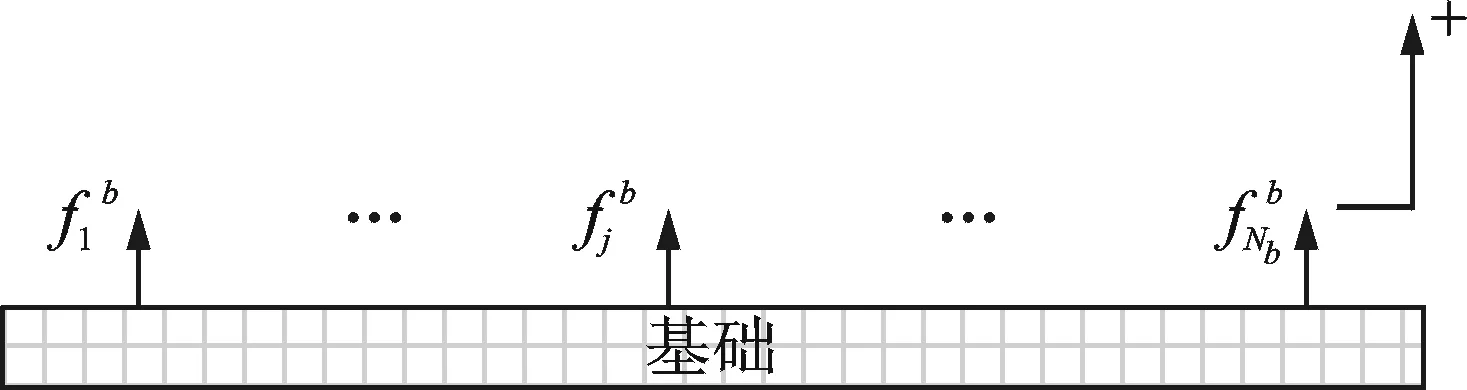
图6 柔性基础受力示意图Fig.6 Load on flexible base

与筏架的推导方法相同，基础的动力学方程可以表示为

Fb=ZbVb

(12)

其中：Fb为基础的力向量；Vb为振速向量；Zb为基础的阻抗矩阵。

根据式(4),(6),(10)～(12)，可得

(13)

式(13)即为笔者建立的全柔性浮筏隔振系统的动力学模型。若已知设备机脚的振动速度Vu，即可求解筏架上层、下层以及基础处的速度，进而计算隔振效果。

2 数值算例

如图7所示，为简化计算，浮筏隔振系统模型中的柔性基础以四端简支矩形板模拟，柔性筏架结构以四边自由方形薄板模拟，不考虑剪力及面内应力的影响。浮筏隔振系统的物理参数为：两台设备的几何参数均为0.8 m×0.4 m×0.4 m，密度为7 800 kg/m3。上层隔振器的额定载荷为300 kg，刚度为1.6×106N/m，下层隔振器的额定载荷为800 kg，刚度为2.0×106N/m，阻尼比为0.04。筏架几何参数为2 m×1 m×0.06 m，结构损耗因子为0.01，筏架前几阶固有频率为80.23, 97.80, 214.53, 221.77, 326.64, 370.89, 382.51和438.99 Hz。基础板几何参数为2 m×1 m×0.02 m，结构损耗因子为0.01，基础板前几阶固有频率为61.64, 98.48, 160.32, 211.25, 247.61, 308.64, 360.93和394.89 Hz。

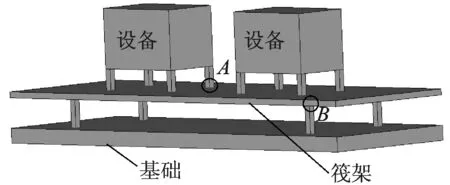
图7 浮筏系统计算模型Fig.7 Numerical simulation model of floating raft

2.1 隔振系统的阻抗特性

考虑隔振器的驻波效应，上层和下层隔振器的驻波频率分别取250 Hz和150 Hz，根据隔振器的刚度可计算出上层和下层隔振器的阻抗，如图8所示。在隔振器驻波频率处阻抗最小，高于隔振器驻波频率时，隔振器阻抗主要受隔振器质量的控制。因此，低于驻波频率时，隔振器刚度视为常刚度，对隔振效果的影响较小，但在高于驻波频率处，对隔振效果的计算将有较大影响。

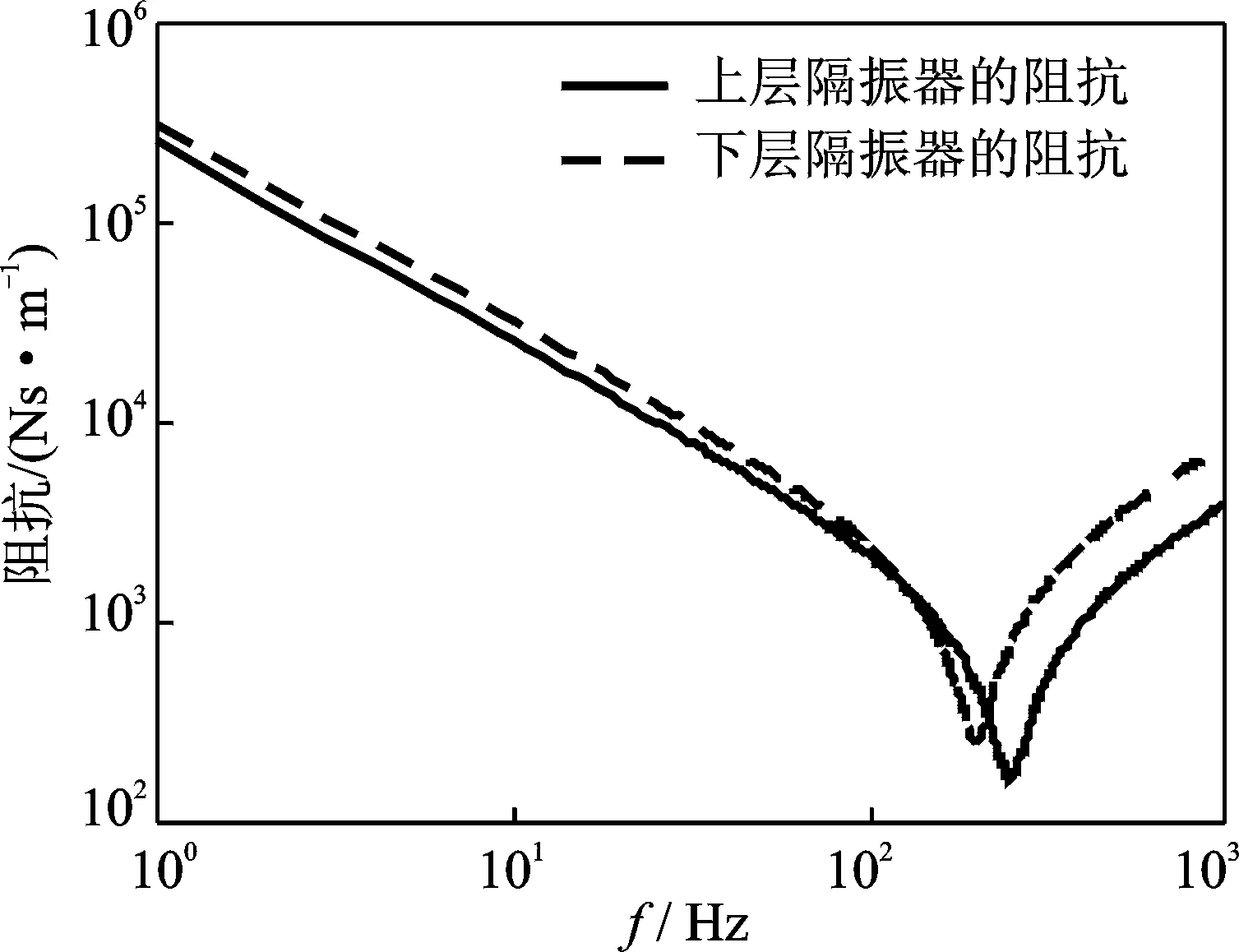
图8 上层和下层隔振器的阻抗Fig.8 Impedance of upper and lower isolators

笔者通过有限元方法获得结构的点到点导纳矩阵，进而计算结构的原点阻抗。筏架上层与隔振器连接点(A点)的原点阻抗如图9所示。由于结构对称，基础上与隔振器连接处4个点的原点阻抗相同，其计算结果如图10所示。筏架为自由边界，因此在低于第1阶模态频率(80.23 Hz)时，筏架的阻抗表现为质量阻抗。对于基础，其边界条件为四边简支，在低于第1阶模态频率(61.64 Hz)时，其阻抗表现为刚度阻抗。

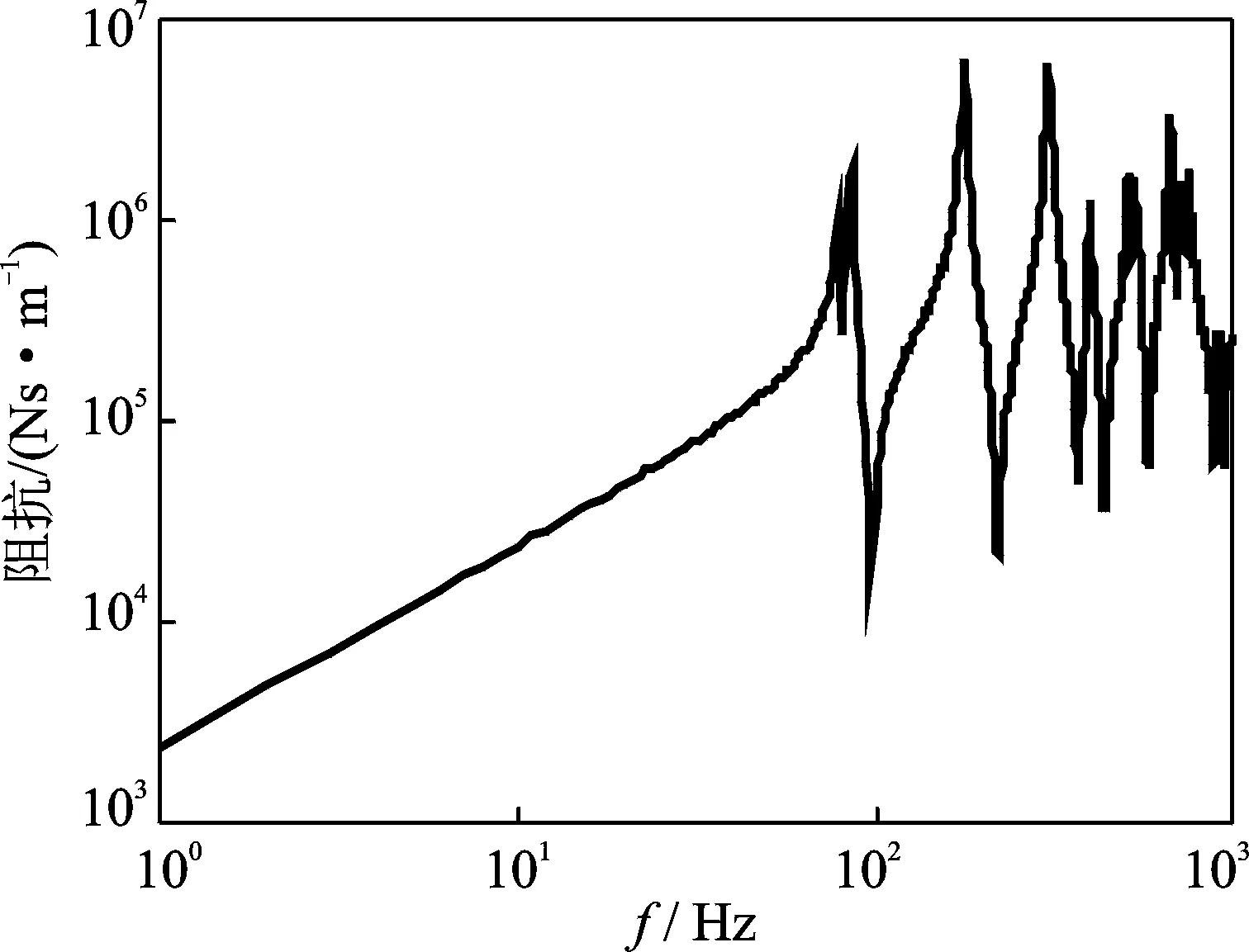
图9 筏架A点的原点阻抗Fig.9 Impedance of raft frame of point A

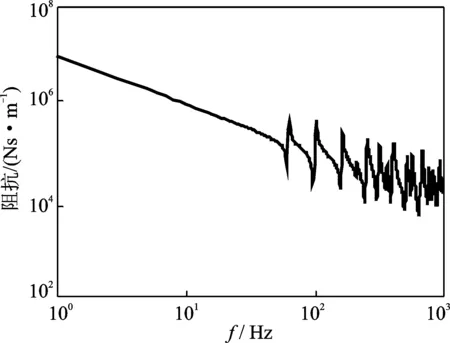
图10 基础的原点阻抗Fig.10 Impedance of base

2.2 筏架刚性与柔性对系统隔振效果的影响

分别将筏架作为刚体与柔性体时，系统的隔振效果如图11和图12所示。

筏架柔性对系统隔振效果的影响主要为：低于筏架的第1阶固有频率时，刚性筏架与柔性筏架模型的计算结果基本吻合，筏架的柔性对隔振效果的影响可以忽略；高于筏架的第1阶固有频率时，筏架的弯曲模态对垂向振动传递计算的结果有较大影响，因此筏架的刚性与柔性对隔振效果的影响主要体现在高频上，在本算例中，振级落差的最大误差可达到40 dB。

图11 刚性筏架与柔性筏架的上层隔振效果Fig.11 Isolation efficiency of upper system

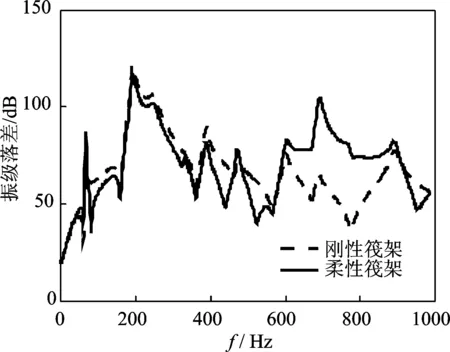
图12 刚性筏架与柔性筏架的总隔振效果Fig.12 Isolation efficiency of global system

2.3 隔振器对隔振效果的影响

在实际工程中，隔振系统的设计除了要考虑隔振效果外，还需要考虑整个隔振系统的刚性，上、下层隔振器刚度对隔振系统的刚性有较大影响。针对此数值算例，假定其他参数不变，笔者模拟并计算了4种隔振器参数的隔振效果，隔振系统刚度如表1所示，其振级落差如图13所示。

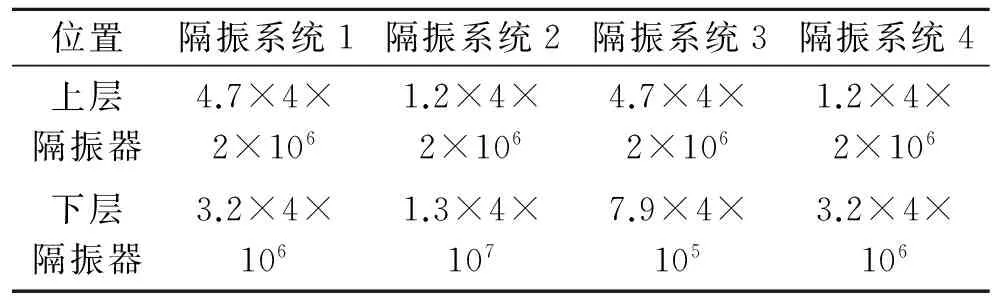
表1 隔振系统刚度

当上、下层隔振器的固有频率相反(隔振系统1和隔振系统2)时，系统的总隔振效果基本相当(如图13(b)所示)，下层隔振器固有频率的降低对上层隔振效果影响不大(如图13(c)所示)，但对总隔振效果有影响(如图13(d)所示)。将上、下层隔振器的固有频率分别相对于隔振系统1降低50%时(隔振系统3和4)，系统的总隔振效果基本相当(如图13(h)所示)。因此，在上、下层隔振刚度的配置上，可以根据浮筏的设计情况采用合适的隔振器配置。

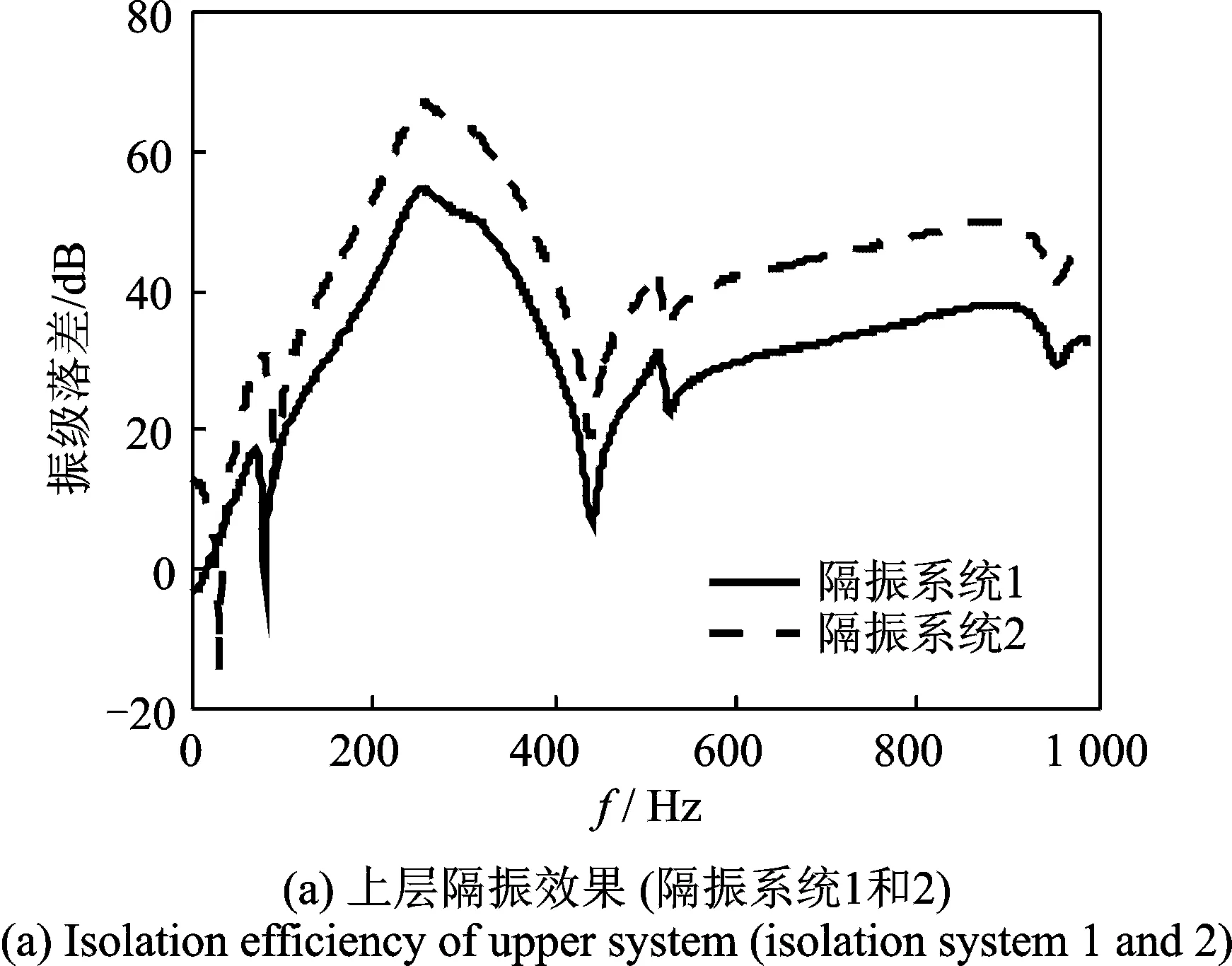
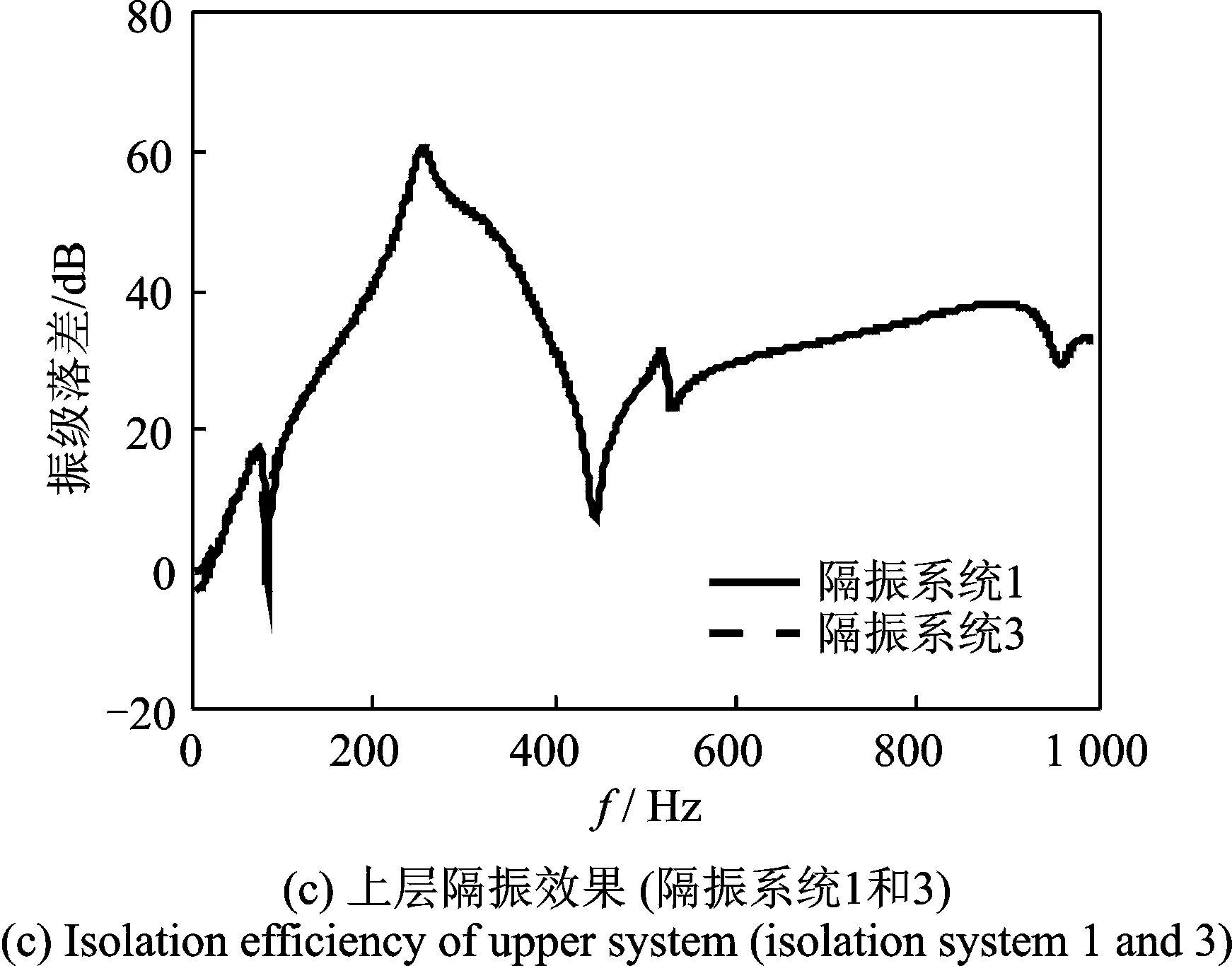
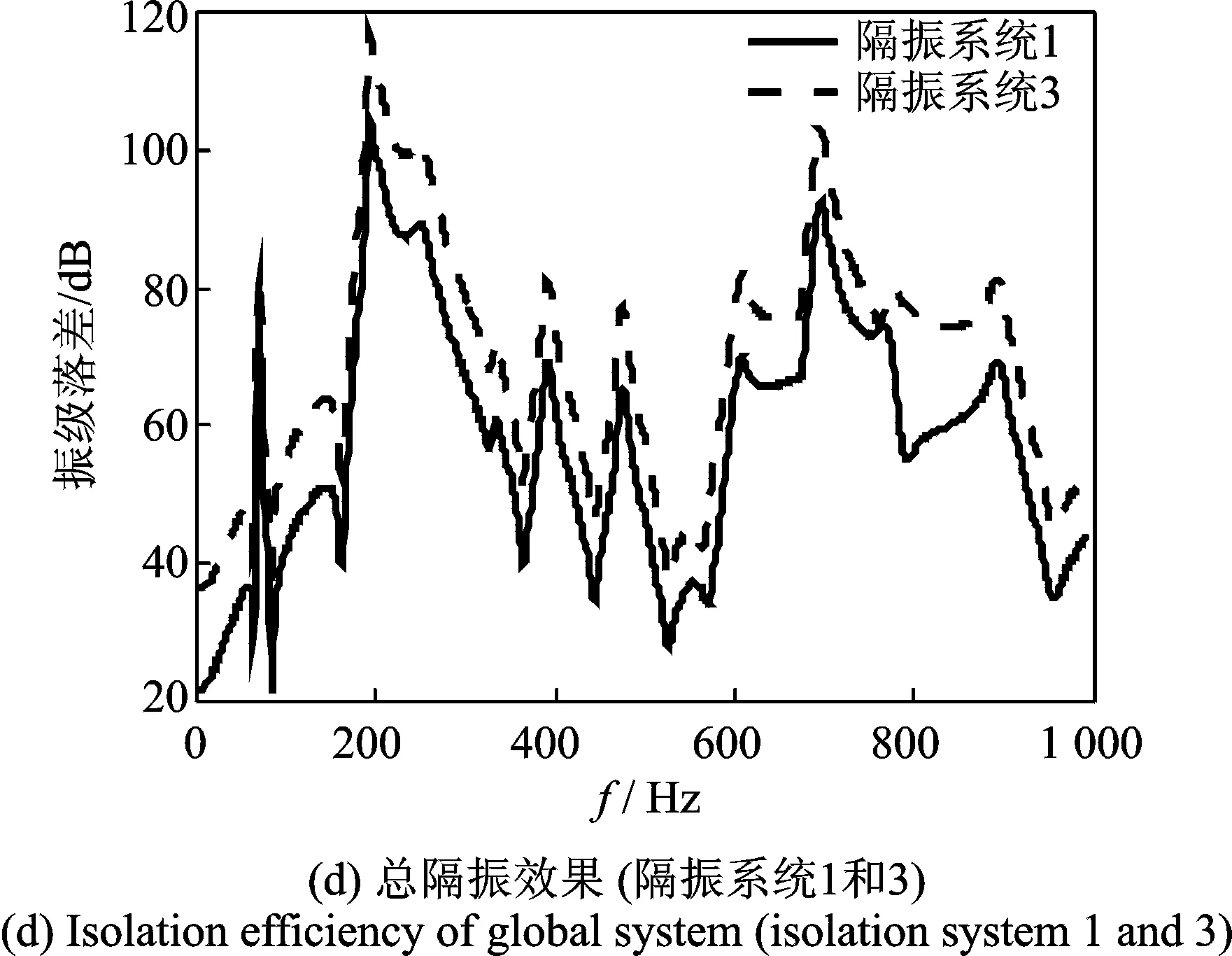
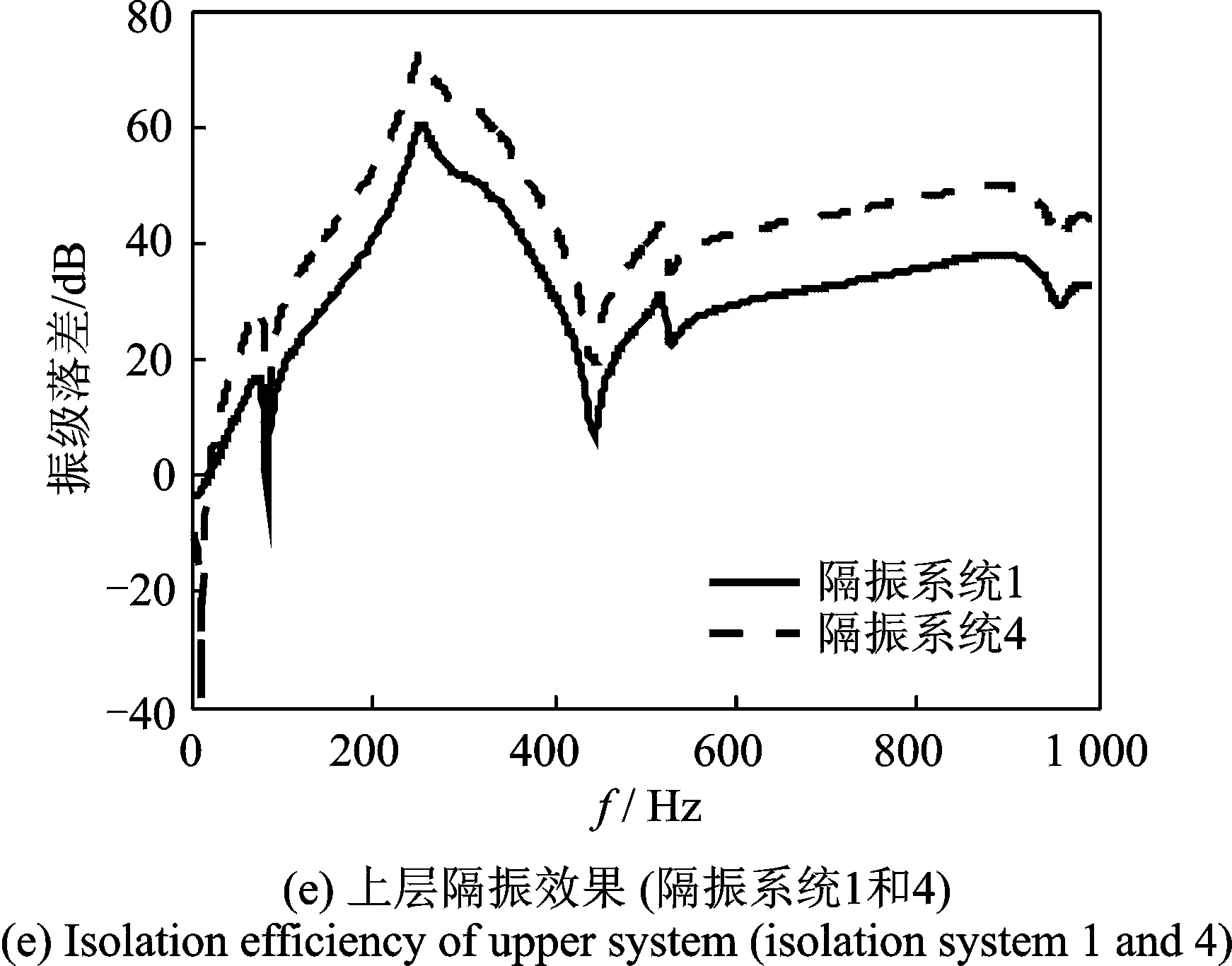
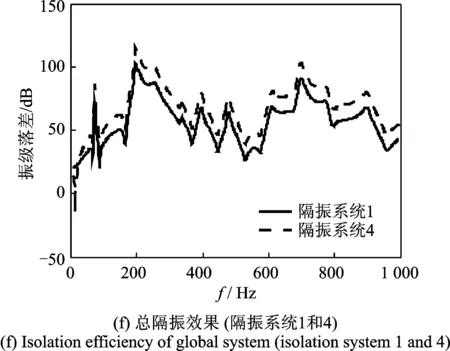
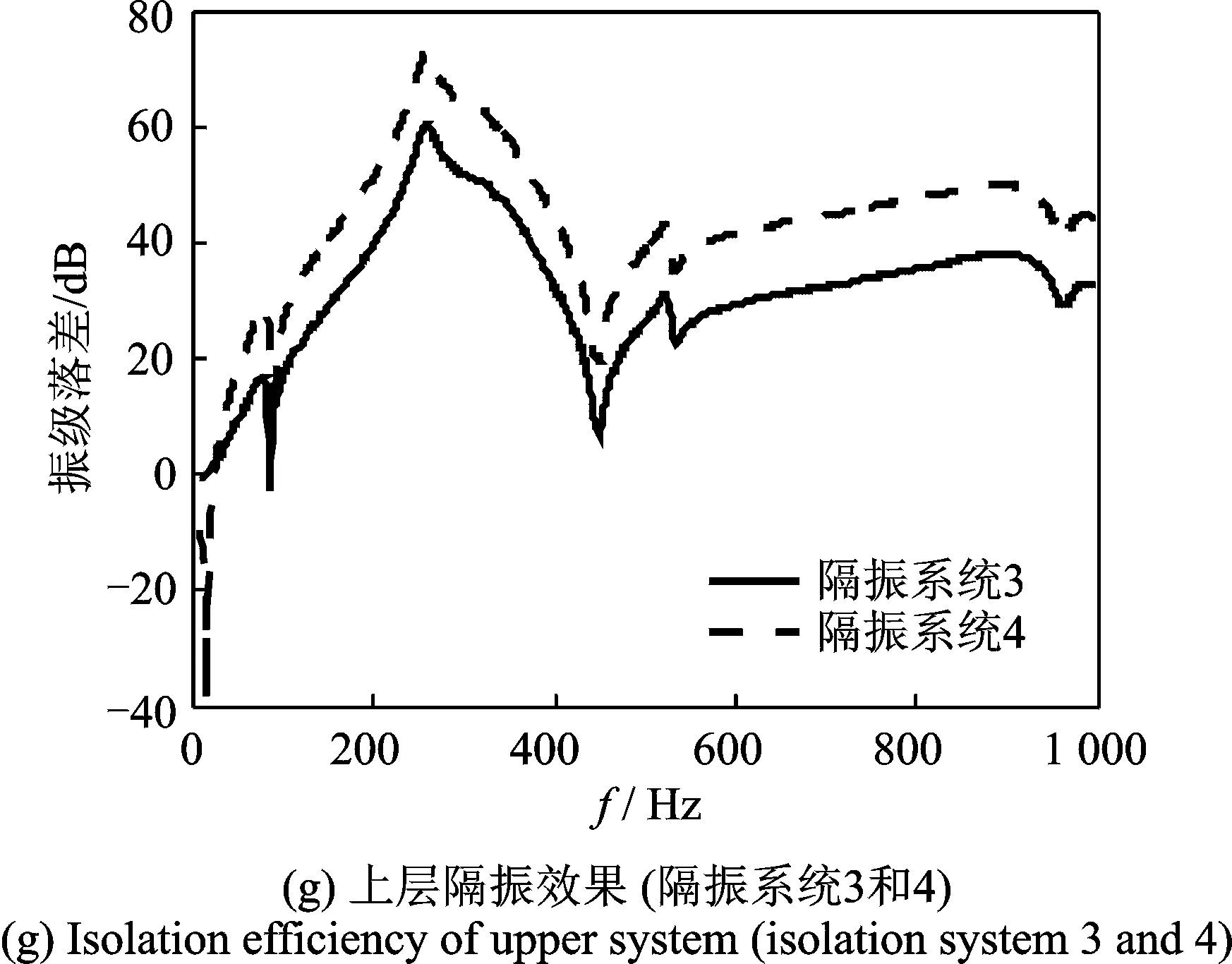
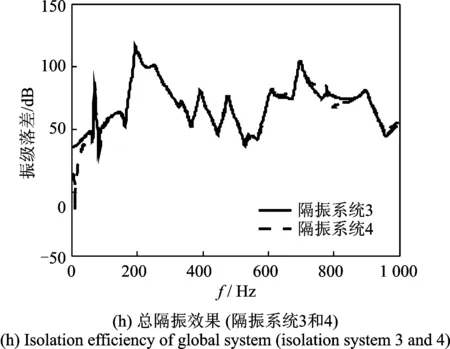
图13 隔振器对隔振效果的影响Fig.13 Isolation efficiency of different isolators

当将筏架与基础视为柔性时，筏架与基础的共振模态与反共振模态对系统的隔振效果有重要影响。在共振模态处，系统的隔振效果降低；在反共振模态处，系统的隔振效果增加。因此，在实际隔振系统设计中，可以根据系统的激励频率对筏架进行逆向设计，使筏架的反共振频率与设备的激励频率吻合，由此来提高系统的隔振效果。同时，隔振器的共振频率对系统的隔振效果也有较大影响。由于在隔振器的共振频率(250Hz)附近，系统的隔振效果增加，因此可以利用隔振器的共振频率来提高隔振系统的隔振效果。

3 结 论

1) 本研究方法将筏架和基础表示为四端参数网络模型，不需要筏架或基础的模态参数，只需要获取筏架与基础的点到点导纳矩阵，而点到点导纳矩阵可以通过有限元计算或实验方法获得。本模型的推导没有理论上的简化，因此计算精度高且模型方程表达简洁。

2) 采用自由振速对设备进行表征，避免了把设备当做刚体而影响模型精度的问题，使得该模型具有比较好的通用性。

3) 在获取了设备的自由振速后，利用本模型可以求出筏架、设备与基础安装点的振动速度，还能够分析设备源特性对系统总隔振效果的影响。因此，笔者提出的方法对浮筏系统隔振系统的设计和工程计算具有重要的理论价值。

[1] 刘保国. 复杂隔振系统振动传递特性及实验研究 [D]. 济南: 山东大学, 2007.

[2] 马丰伟. 复杂隔振系统振动传递特性研究 [D]. 济南: 山东大学, 2006.

[3] Wu Guangming, Shen Rongying, Hua Hongxing. Mode mechanical impedance synthesis method and its application in flexible isolation system [J]. Journal of Ship Mechanics, 2004, 8(6):135-142.

[4] 张树桢, 陈前. 柔性浮筏隔振系统的理论建模与仿真研究 [J]. 船舶力学, 2012, 16(10): 1187-1198.

Zhang Shuzhen, Chen Qian. Modeling and simulation research on flexible floating raft isolation system[J]. Journal of Ship Mechanics, 2012, 16(10): 1187-1198. (in Chinese)

[5] 张星, 朱石坚, 俞翔, 等. 基于ADAMS 刚柔耦合浮筏隔振系统建模及隔振性能分析 [J]. 船海工程, 2010, 39(4): 64-66,69.

Zhang Xing, Zhu Shijian, Yu Xiang, et al. Modeling and vibration performance analysis for rigid-flexible coupling floating raft vibration isolation system based on ADAMS [J]. Ship & Ocean Engineering, 2010, 39(4): 64-66,69. (in Chinese)

[6] 吴广明. 舰船复杂隔振系统建模及其功率流研究 [D]. 上海: 上海交通大学, 2004.

[7] Plunt J. The use of experimental structure-borne sound source data for prediction [C]∥Processing of Inter-Noise.San Francisco:[s.n.],1982:445-448.

10.16450/j.cnki.issn.1004-6801.2017.01.011

*国家自然科学基金资助项目(11202152)

2015-03-03；

2015-06-14

TH113.1; U661.44

王真，女，1976年3月生，博士、副教授。主要研究方向为机械动力学与振动。曾发表《Statistical damage detection based on frequencies of sensitivity-enhanced structures》(《International Journal of Structural Stability and Dynamics》 2008, Vol.8,No.2)等论文。 E-mail: wangzhen@wtu.edu.cn