基于SIE和SVR的液压泵故障定量诊断*

王余奎， 李洪儒， 许葆华

(1.空军勤务学院四站系 徐州，221000) (2.军械工程学院四系 石家庄，050003)

基于SIE和SVR的液压泵故障定量诊断*

王余奎1,2， 李洪儒2， 许葆华2

(1.空军勤务学院四站系 徐州，221000) (2.军械工程学院四系 石家庄，050003)

为更好地实现液压泵故障定量诊断，对故障定量诊断中的退化特征提取和故障程度诊断方法进行研究。针对排列熵算法的不足，提出空间信息熵(spatial information entropy, 简称SIE)的概念，分析了空间信息熵3个参数(时间序列的分区数s、相空间重构的嵌入维数m和延迟时间τ)变化对其性能带来的影响，为其选取提供了依据。仿真分析结果也验证了其作为液压泵退化特征的有效性和优越性。基于空间信息熵算法提取液压泵故障退化特征集，针对退化特征与故障程度之间存在的非线性关系，提出采用果蝇优化算法优化参数的支持向量回归机实现液压泵的故障定量诊断。对实测液压泵振动信号分析结果表明，空间信息熵在表征液压泵故障程度方面具有更好的性能。将果蝇算法优化参数的支持向量回归机用于液压泵的故障定量诊断得到了理想的定量诊断效果，并通过对比分析验证了提出的支持向量回归机模型的有效性和优越性。

液压泵； 定量诊断； 支持向量回归机； 空间信息熵； 果蝇优化算法

引 言

随着维修理论和相关技术的发展，以故障预测技术为核心的基于状态的维修越来越受重视[1]，而基于状态的维修需要对其故障程度和发展趋势进行估计。液压泵作为液压系统的“心脏”，性能好坏影响整个系统；但现有的液压泵振动信号分析方法多集中在故障类型识别和故障位置判定[2-3]，因此研究液压泵故障程度和状态特征之间关系的故障定量诊断具有重要意义[4]。

退化特征提取和故障程度诊断是故障定量诊断的两个关键环节，且是故障预测的基础[5]。液压泵发生故障时，其振动信号表现出强烈的非线性特性，因此液压泵退化特征提取应采用非线性分析方法。随着非线性理论的发展，许多非线性方法被应用到振动信号处理中，如样本熵、Lempel-Ziv指标和模糊熵等[1,6-7]。排列熵(permutation entropy,简称PE)是一种时间序列复杂度指标[8]，已被广泛应用于脑电信号、心音信号、地磁信号以及机械信号的突变检测中[9-11]。但是，通过对PE算法研究发现，PE只考察了重构分量中元素的大小排序关系[8]，没有对重构分量的元素在原时间序列中的分布信息进行分析。为了反映这种分布信息，笔者提出了SIE的概念，拟采用SIE作为液压泵的退化特征。

故障程度判定是故障定量诊断的另一个环节，支持向量机是一种建立在统计学习和结构风险最小化理论基础上的新型机器学习方法，它包括支持向量分类机和支持向量回归机[4](support vector regression,简称SVR)。支持向量机具有理论完备性好、适应性强、全局优化及泛化性能好等优点，被广泛应用于机械故障诊断。在本研究中，将故障定量诊断看成连续过程，采用SVR建立液压泵故障的定量诊断模型，实现液压泵的故障定量诊断。SVR性能的好坏主要取决于惩罚参数c和核函数参数g的选取[12]，常用的参数优化算法包括遗传算法(genetic algorithm,简称GA)和粒子群优化算法(particle swarm optimization algorithm,简称PSOA)。GA存在收敛速度慢、易陷入局部最优的不足；PSOA容易陷入局部最优，且局部搜索能力较差。果蝇优化算法(fruit fly optimization algorithm,简称FOA)是一种全局寻优的群智能算法[13]。该算法具有参数少、计算速度快和全局寻优能力强的优点，已在许多领域得到了推广和应用[14]。本研究采用FOA对SVR的惩罚参数c和核函数参数g进行优化选取，以期得到更好的故障定量诊断效果。

笔者在对PE算法研究的基础上，提出了SIE的概念，通过对仿真信号分析验证了SIE作为故障退化特征的有效性和优越性。将SIE作为液压泵的退化特征，并采用FOA算法优选SVR的参数c和g，采用建立的FOASVR模型实现液压泵的故障定量诊断。通过对实测液压泵振动信号分析，验证了提出方法的合理性和有效性。

1 空间信息熵算法

对于一维时间序列，其PE大小反映了时间序列的复杂程度和随机性[15-16]。当机械设备发生某种故障时，在故障加深的前期，随着故障的加深，其振动信号中由故障引起的确定性成分增加，信号的随机性和复杂度降低[1,5]，此时振动信号的PE值降低[8]。通过分析PE算法的原理可知，PE考虑的是重构分量中各元素在该重构分量中的排序关系，对每个元素在原时间序列中的位置信息没有考虑。为了分析重构分量中各元素在原时间序列中的位置信息，提出了SIE的概念。

1.1 SIE原理

2) 以嵌入维数为m，延迟时间为τ对时间序列进行相空间重构，得到的矩阵为

(1)

(2)

(3)

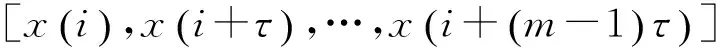
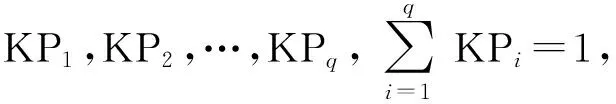
(4)

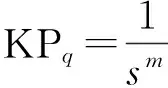
(5)

1.2 参数选取

在SIE的计算过程中，有3个参数需要考虑与选取，分别为时间序列的分区数s、相空间重构的嵌入维数m和延迟时间τ。这里分析以上3个参数对SIE的影响，为其选取提供依据。采用的仿真信号模拟液压泵出现故障时的振动信号为

(6)

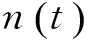
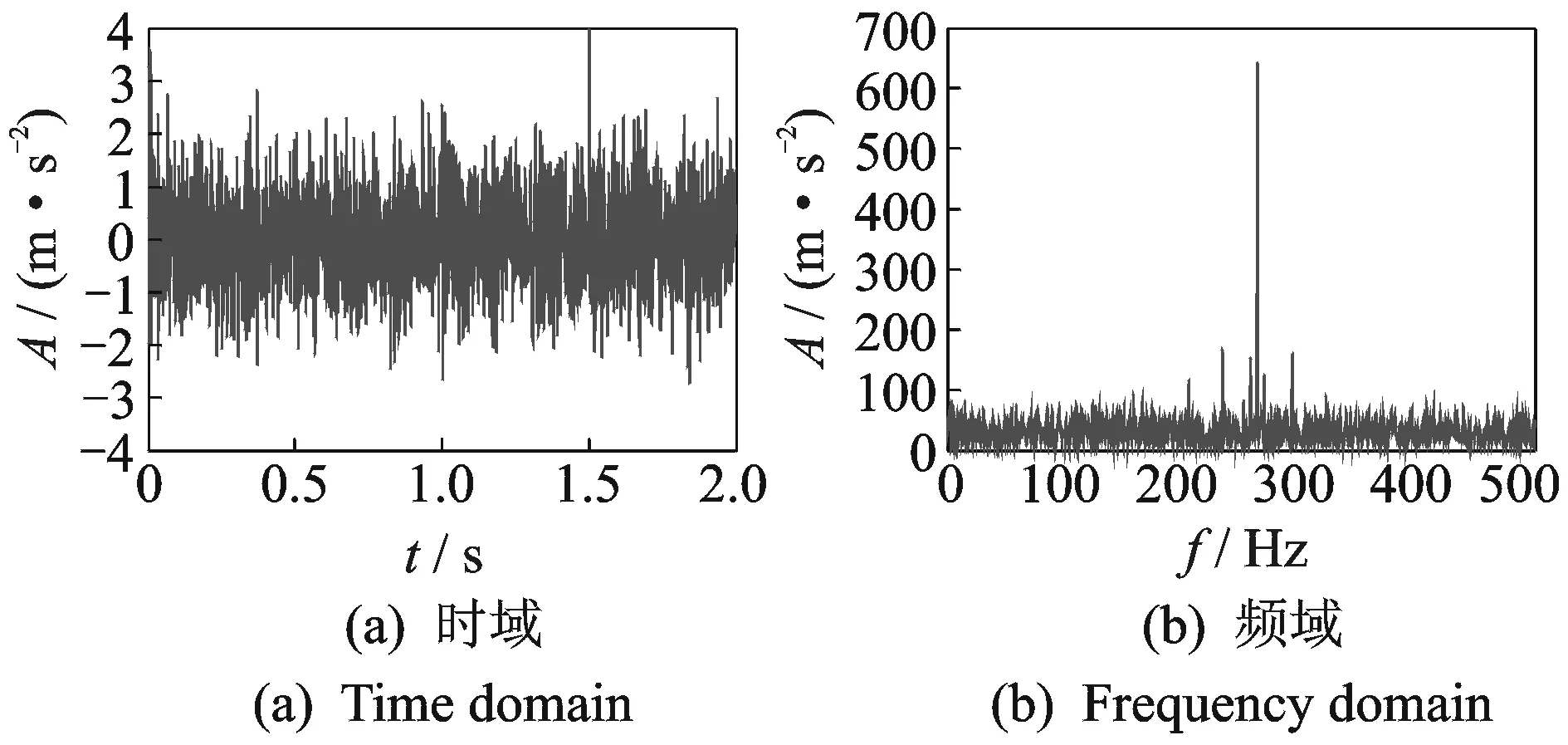
图1 仿真信号波形图Fig.1 Wave form of simulation signal

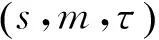
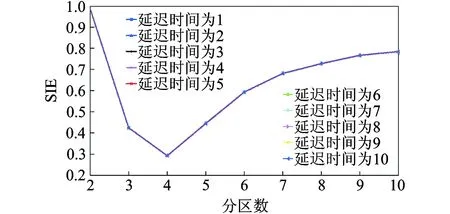
图2 嵌入维数为1时仿真信号空间信息熵Fig.2 The SIE of simulation signal when embedding dimension is 1

图3 嵌入维数为7时仿真信号空间信息熵Fig.3 The SIE of simulation signal when embedding dimension is 7

组合条件下SIE方差

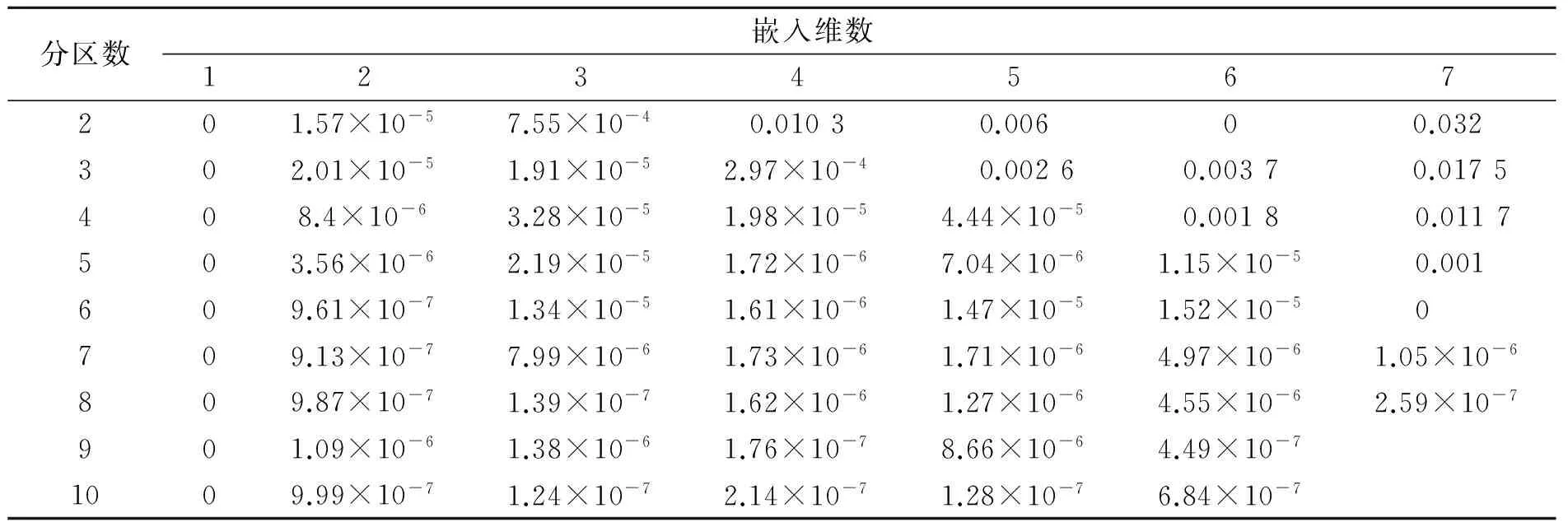
分区数嵌入维数1234567201.57×10-57.55×10-40.01030.00600.032302.01×10-51.91×10-52.97×10-40.00260.00370.0175408.4×10-63.28×10-51.98×10-54.44×10-50.0018 0.0117503.56×10-62.19×10-51.72×10-67.04×10-61.15×10-50.001609.61×10-71.34×10-51.61×10-61.47×10-51.52×10-50709.13×10-77.99×10-61.73×10-61.71×10-64.97×10-61.05×10-6809.87×10-71.39×10-71.62×10-61.27×10-64.55×10-62.59×10-7901.09×10-61.38×10-61.76×10-78.66×10-64.49×10-71009.99×10-71.24×10-72.14×10-71.28×10-76.84×10-7

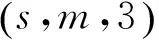
(7)

条件下SIE和SIEz差值

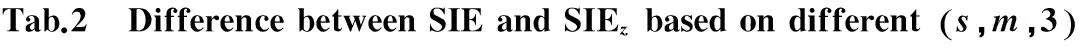
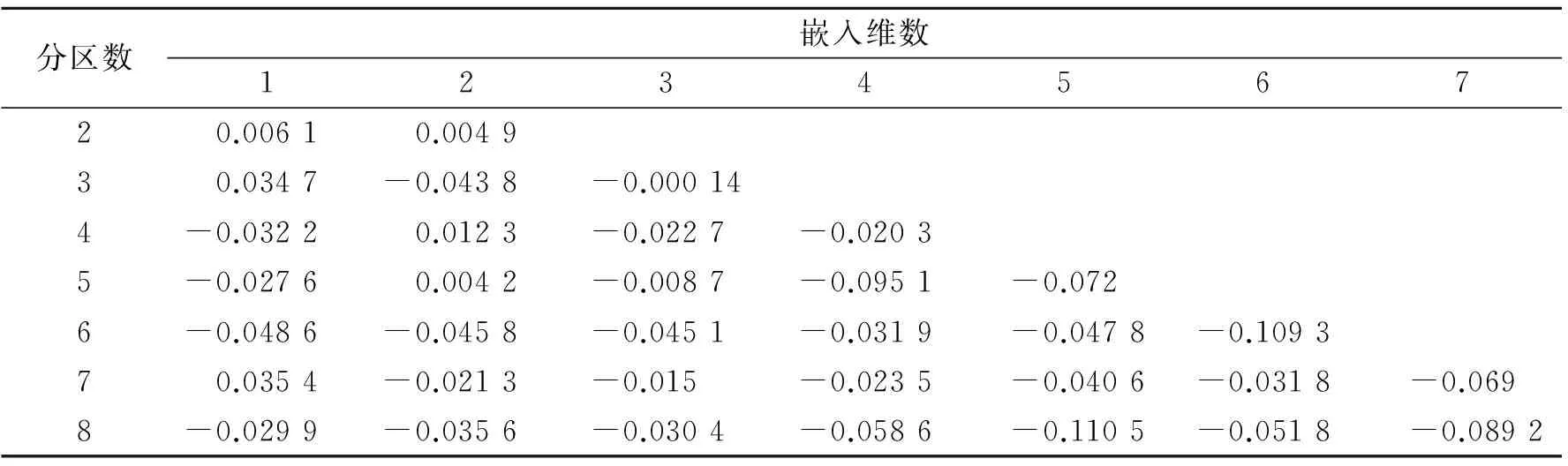
分区数嵌入维数123456720.00610.004930.0347-0.0438-0.000144-0.03220.0123-0.0227-0.02035-0.02760.0042-0.0087-0.0951-0.0726-0.0486-0.0458-0.0451-0.0319-0.0478-0.109370.0354-0.0213-0.015-0.0235-0.0406-0.0318-0.0698-0.0299-0.0356-0.0304-0.0586-0.1105-0.0518-0.0892

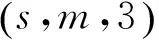
1.3 仿真分析

为了验证SIE反映液压泵故障退化的能力，采用仿真信号模拟液压泵的故障退化过程。设置仿真信号为

(8)

其中：t2xfs(t)用来模拟液压泵故障的加深过程；其余参数和变量与仿真信号x(t)一致；设置xd(t)的采样点数为N=20 480；采样频率为1 024 Hz。

为了研究噪声强度对SIE的影响，对仿真信号加入白噪声，使信号的信噪比分别为2，1，-1，-2，-3 dB以及不加噪声6种情况。图4为不加噪声时液压泵故障退化的仿真信号波形图。

图4 液压泵退化仿真信号波形图Fig.4 Wave form of the degradation simulation signal of hydraulic pump

计算不加噪声时xd(t)的SIE。将xd(t)等分为10组并按顺序标记，每段数据点数为2 048，采用这样的10组数据近似模拟液压泵故障程度不断加深的过程。计算以上10组数据的SIE，结果如图5所示。为对比分析SIE描述液压泵故障退化的能力，计算以上10组数据的PE值，根据文献[12]的经验，笔者取嵌入维数m=4，延迟时间τ=3作为PE计算过程中的参数，计算结果如图6所示。采用同样的方式计算5种加噪信号的SIE和PE，结果分别如图5和图6所示。

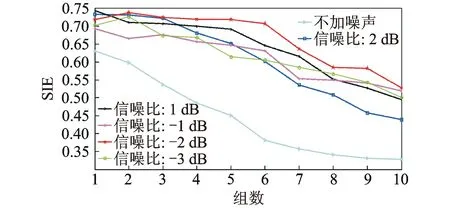
图5 液压泵退化仿真信号的SIEFig.5 SIE of the degradation simulation signal of hydraulic pump

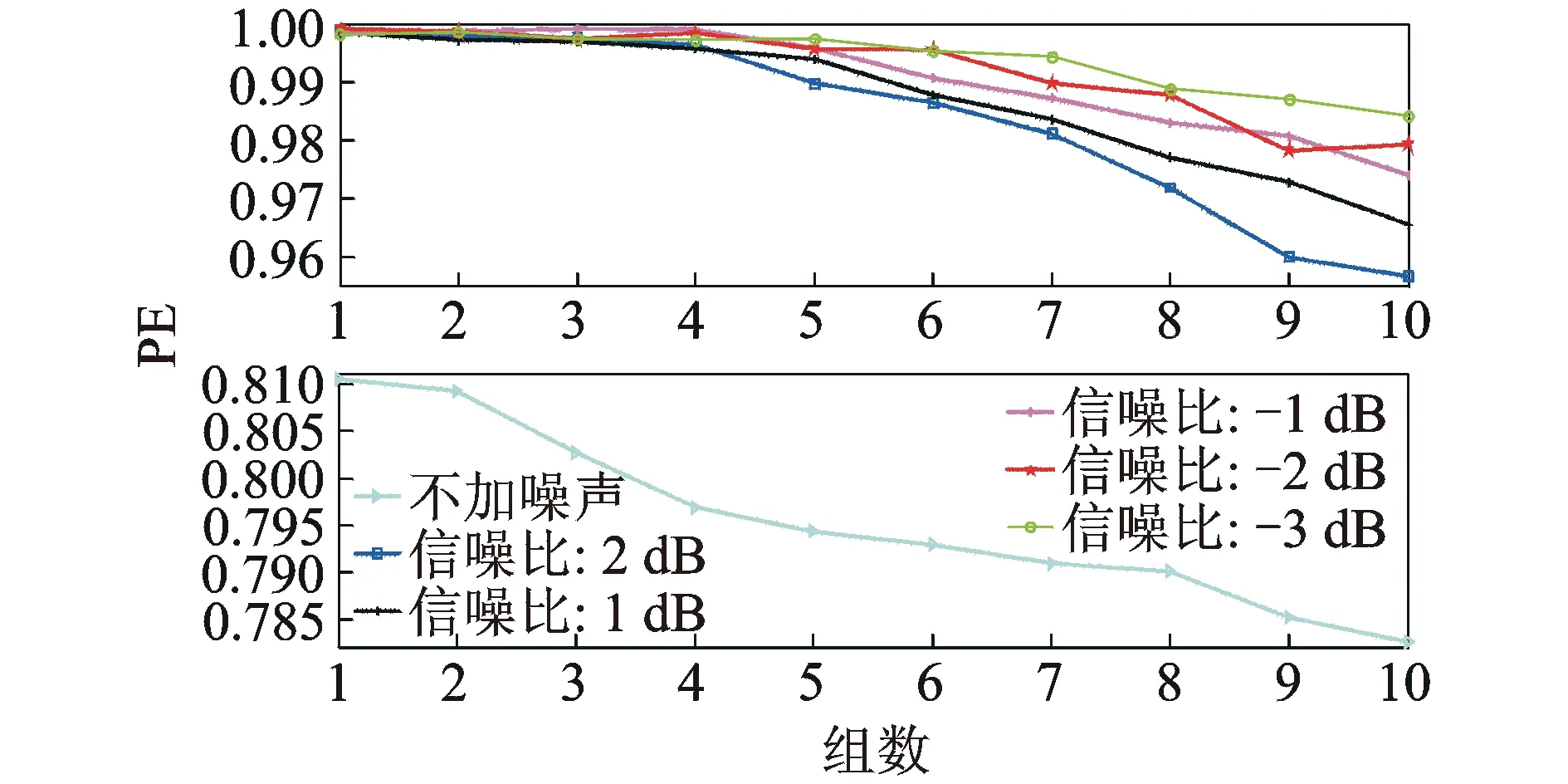
图6 液压泵退化仿真信号的PEFig.6 PE of the degradation simulation signal of hydraulic pump

图5和图6分别展现了SIE和PE在不同噪声背景下对液压泵故障程度的表征能力。分析两图可知：a.随着故障程度的加深，两参数都呈现出明显的下降趋势，反映了信号随机性和复杂度的降低；b.不论在何种噪声背景下，随着故障程度的加深，SIE下降的幅度都大于PE，体现了SIE对故障程度变化更强的反映能力，也验证了SIE能更好的在细节上反映时间序列随机性和复杂度的变化；c.在噪声强度较低时，SIE和PE随着组别的增加呈现出稳定的下降趋势，但在噪声较强时，两参数出现了先上升后下降的情况，原因是在故障微弱阶段，强噪声背景对SIE和PE表征故障退化的能力会产生影响。

2 液压泵故障定量诊断策略

退化特征提取和故障程度诊断是液压泵故障定量诊断的两个环节。笔者从液压泵振动信号中提取SIE作为其退化特征，采用SVR算法实现其故障的定量诊断[4]。同时提取PE作为退化特征并建立SVR模型实现液压泵故障定量诊断，以对比SIE作为退化特征用于液压泵故障定量诊断的性能。SVR模型的惩罚因子c和核函数参数g对其性能影响很大，本研究采用FOA算法对g和c的取值进行优选，FOA寻优原理见文献[14]。采用SVR实现液压泵定量故障诊断的策略如图7所示。首先，对液压泵振动信号分析提取退化特征，并将提取特征分为训练特征集和测试特征集；然后，基于训练集采用FOA算法对SVR模型的参数进行优化；最后，建立故障定量诊断模型，基于测试集实现液压泵的故障定量诊断。

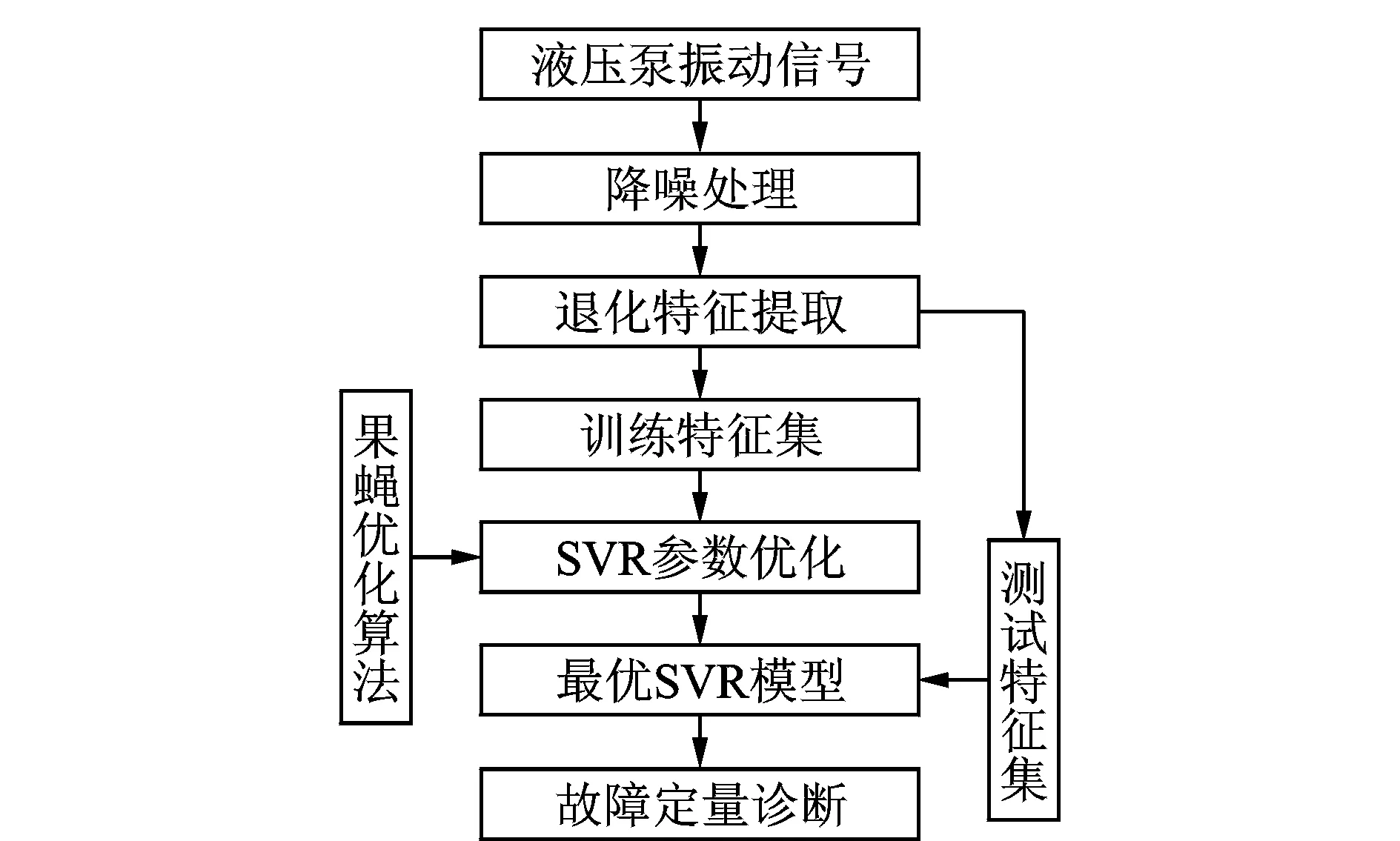
图7 液压泵故障定量诊断策略Fig.7 The quantitative diagnosis strategy of Hydraulic Pump fault

3 实例分析

3.1 数据采集及处理

实测液压泵振动信号来自于自液压泵试验台[18]，如图8所示。液压泵型号为SY-10MCY14-1EL，采用型号为Y132M-4的电机驱动，其额定转速为1 480 r/min。选用CA-YD-139型压电式加速度传感器与液压泵端盖刚性连接，使用DH-5920型振动信号采集仪进行数据采集。试验系统框图如图9所示。笔者主要对液压泵出现单松靴故障时的振动信号进行分析，为获得较为贴近实际的不同程度松靴故障的振动信号，液压泵故障采用装备检修时换下的带有不同程度松靴故障的柱塞代替正常柱塞的方式模拟。为界定松靴故障的程度，定义松靴度为滑靴与柱塞间能够发生的最大轴向位移量。采用游标卡尺测量试验中所用的5个松靴柱塞的松靴度分别为0.12,0.18,0.3,0.42和0.64 mm。采集5种程度松靴以及正常状态下的液压泵振动信号各100组，每组信号采样点数为2 048，数据采样频率为50 kHz，采样间隔为30 s，试验过程中试验台主溢流阀压力为10 MPa，电机转速为其额定转速。

采集部分振动信号如图10所示，由试验中采用柱塞的松靴度可知，每种状态比前一状态的松靴度增加量分别为0.12，0.06，0.12，0.12和0.22 mm，是一个由轻到重的过程，所采集振动信号的幅值表现出由小到大的趋势，大致反映了松靴度的加深情况，但仅从振动信号时域图不能有效判定松靴度的大小。

图8 液压泵试验台Fig.8 Test bench of hydraulic pump

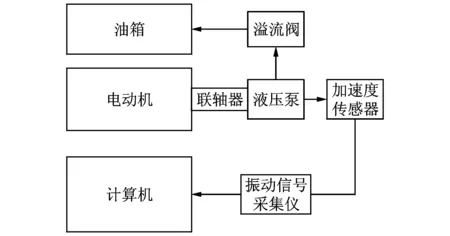
图9 试验系统框图Fig.9 Diagram of the test rig

图10 采集的部分振动信号Fig.10 Waveform of collected vibration signal

3.2 退化特征提取

由仿真分析可知，强噪声背景下SIE和PE描述微弱故障退化的能力受噪声影响较大，因此在对实测信号分析前有必要对其进行降噪。笔者采用文献[18]提出的CNC降噪法对实测信号进行降噪处理。为了验证SIE表征液压泵故障程度的能力，并与PE进行对比，从正常和5种程度松靴的样本中各任取10组，分别计算其PE和SIE，如图11所示。

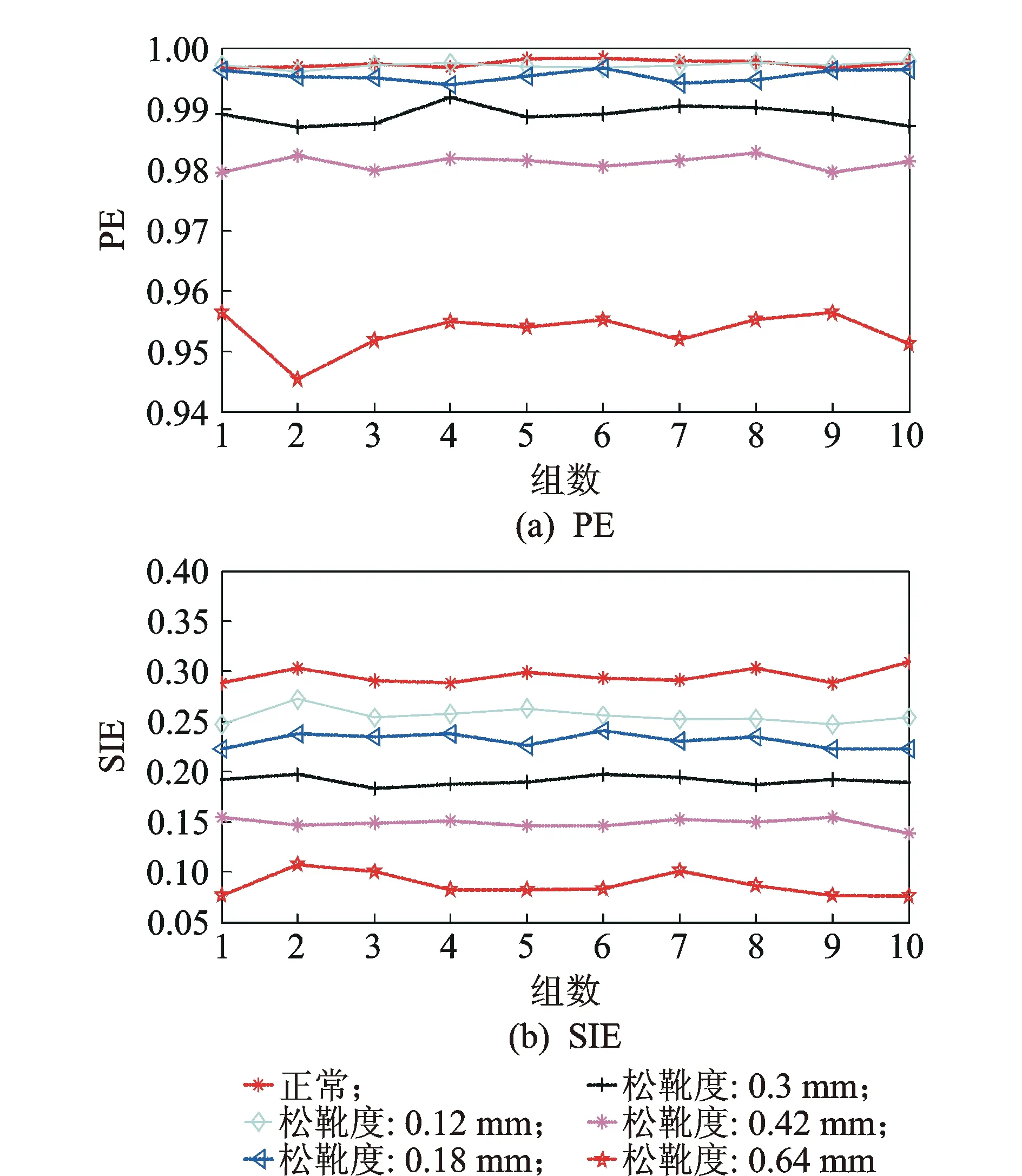
图11 松靴样本的SIE和PEFig.11 SIE and PE of loosing boot samples

分析图10和图11得出以下结论：a.正常样本的SIE和PE值最大，说明正常状态下液压泵振动信号的随机性和复杂度最大；b.随着故障程度的加深，SIE和PE都明显下降，说明信号随机性和复杂度随故障程度的加深而降低；c.SIE和PE都能有效区分不同程度的松靴故障，但从对故障程度的表征能力上分析，SIE的性能更加优越：d.在松靴度由小到大发生定量变化时，10组样本SIE平均值的减少量分别为0.040 3，0.023 4，0.397，0.041 1和0.061 9，SIE变化量与松靴度变化量有相对较好的比例关系，SIE能较好地表征松靴度的变化；e.PE对松靴度的表征能力明显弱于SIE，10组样本PE平均值的减少量分别为6.4×10-4，0.001 7，0.006 4，0.008和0.027 8；f.松靴度为0.12 mm样本的PE值和正常样本PE值以及松靴度为0.18 mm样本的PE值出现了交叉现象。

将正常状态作为松靴状态的一种特殊情况，从6种程度故障的样本中各任选60组作为样本集。为了对比SIE和PE在液压泵故障定量诊断中的性能，基于样本集分别提取SIE特征集和PE特征集，其步骤为：a.采用经验模态分解(empirical mode decomposition,简称EMD)算法对每个样本进行分解，基于每个內禀模态函数(intrinsic mode function,简称IMF)与原信号的互相关系数[19]和互信息值[20]乘积绝对值的大小确定敏感IMF，取较敏感的前4个IMF作为分析对象；b.提取每个敏感IMF的SIE和PE，即得到60(4维的SIE特征集和PE特征集。图12为从SIE特征集和PE特征集中任选10组特征向量的第1维特征值。

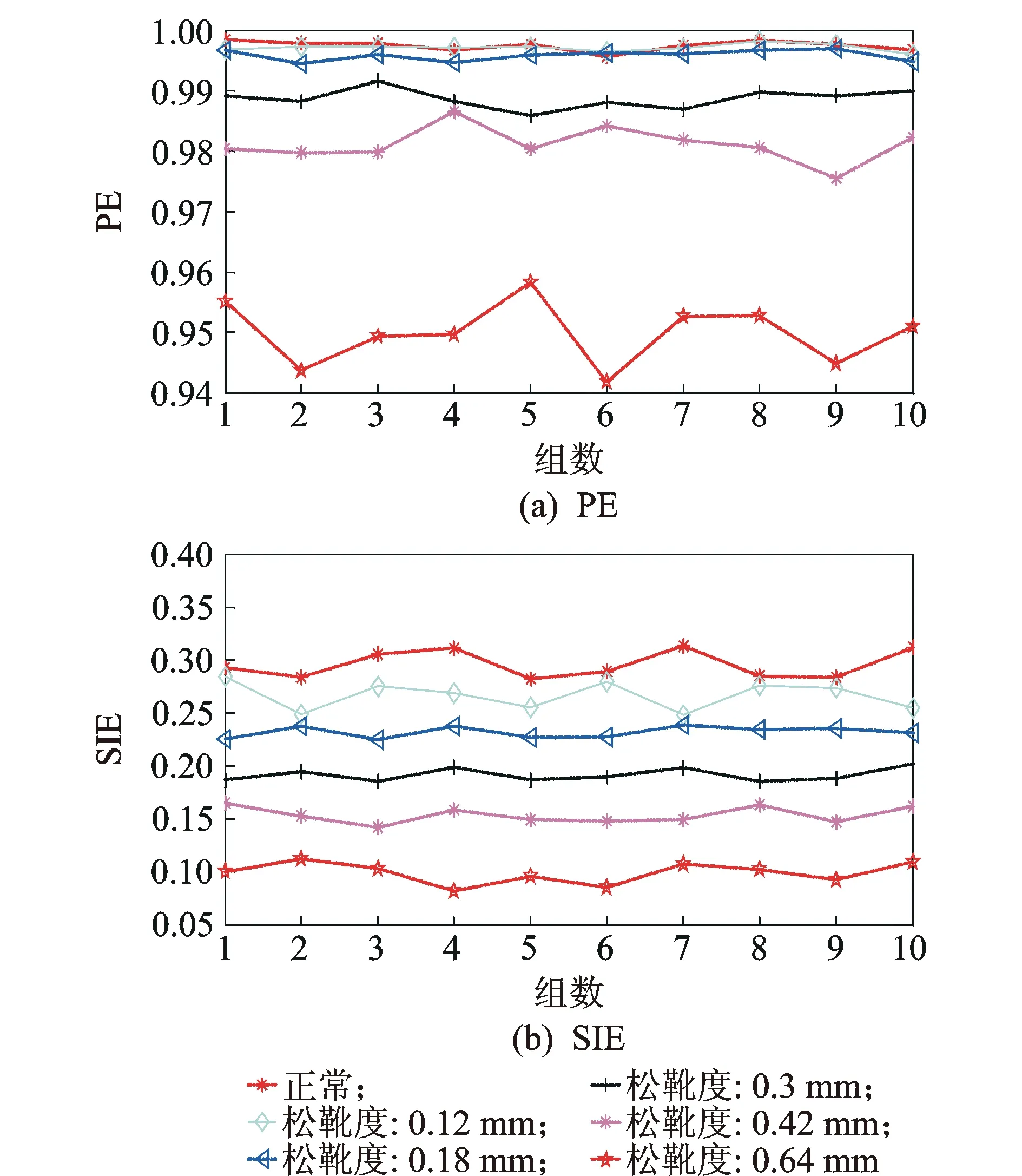
图12 提取特征向量的第1维特征Fig.12 The first feature of the extracted feature vector

3.3 故障定量诊断模型训练及应用

基于SIE特征集和PE特征集分别建立液压泵故障定量诊断模型，以液压泵松靴度为定量诊断目标值，实现液压泵的故障定量诊断。对于SIE特征集，取其前30组作为训练集，后30组作为测试集。训练集分别采用FOA算法、PSO算法和GA算法对SVR的模型参数c和g寻优，3种算法的主要参数设置[14]如下：最大迭代次数和种群规模分别为100和10；FOA算法的初始坐标为(5 rand(1,1)，5 rand(1,1))，迭代步长为20；PSO算法的局部搜索参数为1.5，全局搜索参数为1.7；GA算法的交叉概率为0.7，变异概率为0.1。以训练样本的最小均方误差作为个体适应度，3种算法寻优过程中适应度变化曲线如图13(a)所示，寻优结果如表3所示。对于PE特征集，采用同样的方式对其SVR的模型参数进行寻优，寻优过程中3种算法的适应度变化曲线如图13(b)所示，寻优结果如表3所示。

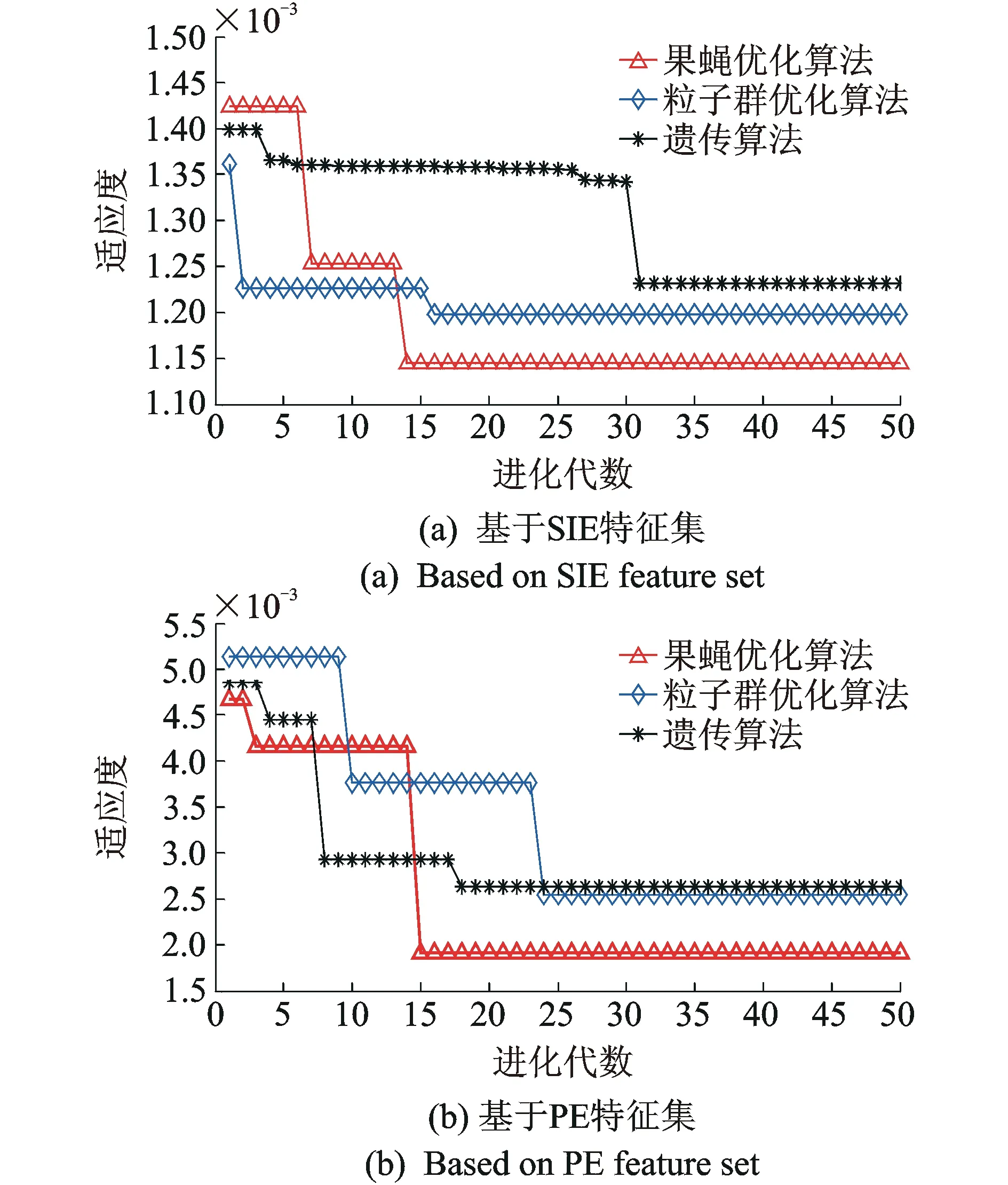
图13 参数寻优适应度曲线Fig.13 Adaption curves of parameters optimizing

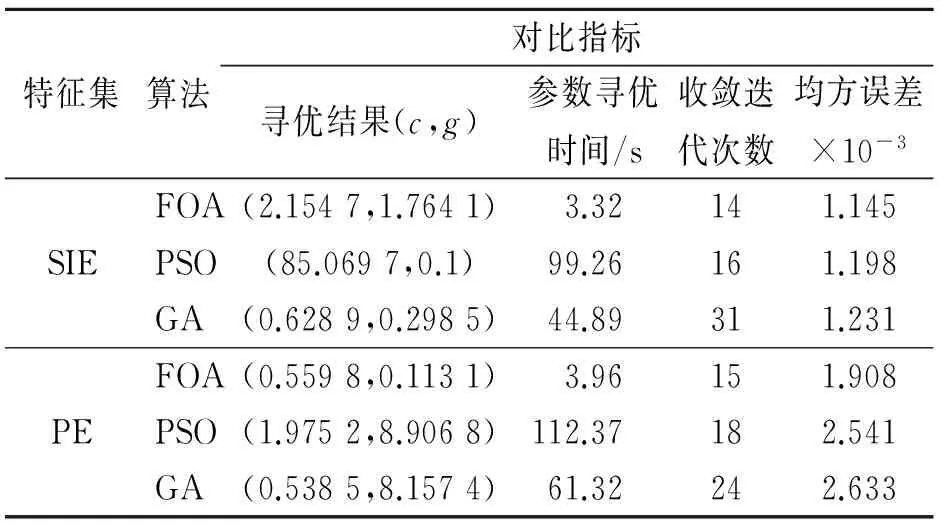
特征集算法对比指标寻优结果(c,g)参数寻优时间/s收敛迭代次数均方误差×10-3SIEFOA(2.1547,1.7641)3.32141.145PSO(85.0697,0.1)99.26161.198GA(0.6289,0.2985)44.89311.231PEFOA(0.5598,0.1131)3.96151.908PSO(1.9752,8.9068)112.37182.541GA(0.5385,8.1574)61.32242.633

分析图13和表3可知，不论采用哪种参数优化算法，基于SIE特征集建立的SVR模型在训练集上的诊断误差都更小，得到了更高的故障定量诊断精度，且参数优选的运行时间和迭代代数都要小于基于PE特征集的情况。另外，不论是基于SIE特征集还是PE特征集，FOA算法的参数寻优性能都优于另外两种算法。

基于SIE训练特征集，分别采用以上3种算法优选的参数建立SVR模型，采用建立的模型对测试集进行故障定量诊断，如图14所示。对于PE特征集，采用同样的方式建立故障定量诊断模型并实现定量诊断，如图15所示。为了进一步验证SIE和PE在液压泵故障定量诊断中的性能，分别计算基于SIE特征集建立的SVR模型和基于PE特征集建立的SVR模型的模型训练时间、诊断值与实际松靴度的均方误差、诊断值与实际松靴度的绝对平均误差、诊断值与实际松靴度的最大误差及诊断值与实际松靴度的相关系数等指标，如表4所示。

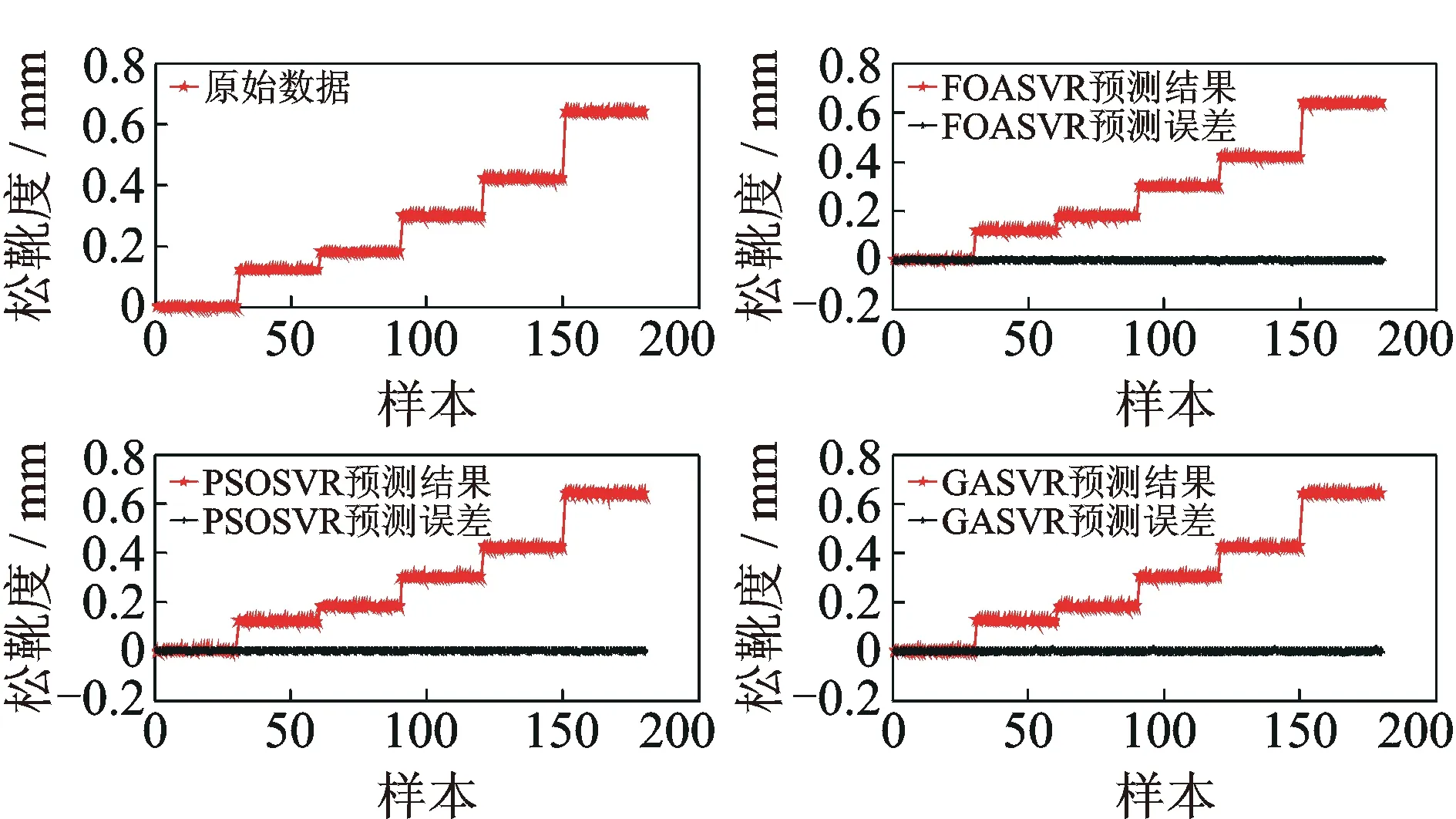
图14 基于SIE特征集建立SVR模型的定量诊断结果Fig.14 Testing results of the SVR model based on SIE

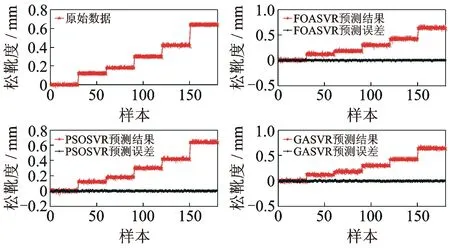
图15 基于PE特征集建立SVR模型的定量诊断结果Fig.15 Testing results of the SVR model based on PE

特征集模型对比指标相关系数/%均方误差×10-3绝对平均误差×10-3最大误差×10-3SIEFOASVR99.4731.1491.0782.746PSOSVR99.2691.2081.1202.982GASVR99.0571.2411.1634.369PEFOASVR99.2102.1931.8754.311PSOSVR98.9572.7462.5405.742GASVR98.6222.8012.5716.859

分析图14，15和表4可以得出以下结论：a.不论是采用PE还是SIE作为退化特征，都能够有效诊断出液压泵松靴度；b.基于SIE特征集建立的SVR模型诊断值与实际松靴度误差更小，诊断值更加贴近液压泵的松靴度，故障定量诊断的精度更高；c.与PSO和GA相比，FOA在优化SVR模型参数上性能更加优越。

4 结 论

1) 空间信息熵基于重构序列中元素在原时间序列中位置信息的变化反映了时间序列复杂度和随机性的变化，与排列熵相比能更好地在细节上反映时间序列的动力学变化，能更好地表征液压泵的故障程度。

2) 空间信息熵3个参数的选择可以参考以下原则：分区数取值不宜过大，且应不小于嵌入维数；嵌入维数应在3～7的范围内取值；在以上条件下，延迟时间可以在1～10内任意取值。

3) 实测液压泵振动信号分析结果表明：空间信息熵具有更好的故障程度表征能力；与排列熵相比，采用空间信息熵作为退化特征实现液压泵故障定量诊断能得到更高的诊断精度；采用FOA优选液压泵故障定量诊断模型参数具有更优越的性能。

[1] 张建宇, 张随征, 管磊, 等. 基于多小波包样本熵的轴承损伤程度识别方法[J]. 振动、测试与诊断, 2015, 35(1):128-132.

Zhang Jianyu, Zhang Suizheng, Guan Lei, et al. Pattern recognition of bearing defect severity based on multiwavelet packet sample entropy method[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(1):128-132. (in Chinese)

[2] Du Jun, Wang Shaoping, Zhang Haiyan. Layered clustering multi-fault diagnosis for hydraulic piston pump[J]. Mechanical Systems and Signal Processing, 2013(36):487-504.

[3] Zhao Zhen, Jia Mingxing, Wang Fuli, et al. Intermittent chaos and sliding window symbol sequence statistics-based early fault diagnosis for hydraulic pump on hydraulic tube tester[J]. Mechanical Systems and Signal Processing, 2009(23):1573-1585.

[4] 鞠华, 沈长青, 黄伟国, 等. 基于支持向量回归的轴承故障定量诊断应用[J]. 振动、测试与诊断, 2014, 34(4):767-771.

Ju Hua, Shen Changqing, Huang Weiguo, et al. Quantitative diagnosis of bearing fault based on support vector regression[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(4): 767-771. (in Chinese)

[5] 王冰, 李洪儒, 许葆华. 基于多尺度形态分解谱熵的电机轴承预测特征提取及退化状态评估[J]. 振动与冲击, 2013, 32 (22):124-128.

Wang Bing, Li Hongru, Xu Baohua. Motor bearing forecast extracting and degradation status identification based on multi-scale morphological decomposition spectral entropy[J]. Journal of Vibration and Shock, 2013, 32(22): 124-128. (in Chinese)

[6] 董新峰,张为民,邓松. 基于Lempel-Ziv指标的主轴系统退化[J]. 振动、测试与诊断, 2015,35(1):17-23.

Dong Xinfeng, Zhang Weimin, Deng Song. The research for the degradation of spindle of machine tool based on Lempel-Ziv index[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(1):17-23. (in Chinese)

[7] 杨宇, 潘海洋, 程军圣. VPMCD和模糊熵在转子系统故障诊断中的应用[J]. 振动、测试与诊断, 2014, 34(5):791-795.

Yang Yu, Pan Haiyang, Cheng Junsheng. The application of VPMCD and fuzzy entropy in rotor system fault diagnosis[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34 (5): 791-795. (in Chinese)

[8] Bandt C, Pompe B. Permutation entropy: a natural complexity measure for time series[J]. Physical Review Letters, 2002, 88(174102):1-4.

[9] Nicolaou N, Georgiou J. Detection of epileptic electroencep-alogram based on permutation entropy and support vector machines[J]. Expert Systems with Applications, 2012, 39: 202-209.

[10]Yan Ruqing, Liu Yongbin, Gao R X. Permutation entropy: a nonlinear statistical measure for status characterization of rotary machines[J]. Mechanical Systems and Signal Processing, 2012, 29: 474-484.

[11]Ouyang Gaoxiang, Li Jing, Liu Xianzeng. Dynamic character-ristics of absence EEG recordings with multiscale permutation entropy analysis[J]. Epilepsy Research, 2013, 104: 246-252.

[12]吴坚,赵阳,何春. 基于支持向量机回归算法的电子机械制动传感器系统故障诊断[J].吉林大学学报, 2013, 43(5):1178-1183.

Wu Jian, Zhao Yang, He Chun. Fault detection and diagnosis of EMB sensor system based on SVR[J]. Journal of Jilin University, 2013, 43(5):1178-1183. (in Chinese)

[13]Pan Wentao. A new fruit fly optimization algorithm: taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012, 26 (1): 69-74.

[14]宁剑平, 王冰, 李洪儒, 等. 递减步长果蝇优化算法及应用[J]. 深圳大学学报:理工版, 2014, 31 (4):367-373.

Ning Jianping, Wang Bing, Li Hongru, et al. Research on and application of diminishing step fruit fly optimization algorithm [J]. Journal of Shenzhen University: Science and Engineering, 2014, 31 (4):367-373. (in Chinese)

[15]刘永斌, 龙潜, 冯志华, 等. 一种非平稳、非线性振动信号检测方法的研究[J]. 振动与冲击, 2007, 26(12):131-134.

Liu Yongbing, Long Qian, Feng Zhihua, et al. Detection method for nonlinear and non-stationary signals[J]. Journal of Vibration and Shock, 2007, 26(12):131-134. (in Chinese)

[16]冯辅周,司爱威,江鹏程. 小波相关排列熵和HMM在故障预测中的应用[J]. 振动工程学报, 2013, 26(2):269-275.

Feng Fuzhou, Si Aiwei, Jiang Pengcheng. Application of wavelet correlation permutation entropy and hidden markov model to fault prognostic[J]. Journal of Vibration Engineering, 2013, 26 (2): 269-275. (in Chinese)

[17]姜万录, 刘云杰, 朱勇. 小波脊线解调与两次EMD分解相结合的故障识别方法及应用研究[J]. 仪器仪表学报, 2013, 34(5): 1131-1138.

Jiang Wanlu, Liu Yunjie, Zhu Yong. Research on wavelet ridge demodulation and twice EMD-based fault identification method and its application[J]. Chinese Journal of Scientific Instrument, 2013, 34(5):1131-1138. (in Chinese)

[18]Wang Yukui, Li Hongru, Ye Peng. Fault feature extraction of hydraulic pump based on CNC De-noising and HHT[J]. Journal of Failure Analysis and Prevention, 2015,15(1):139-151.

[19]苏文胜, 王奉涛, 张志新, 等. EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]. 振动与冲击, 2010, 29(3): 18-21.

Su Wensheng, Wang Fengtao, Zhang Zhixin, et al. Application of EMD de-noising and spectral kurtosis in early fault diagnosis of rolling element bearings[J]. Journal of Vibration and Shock, 2010, 29(3):18-21. (in Chinese)

[20]张志刚, 石晓辉, 施全, 等. 基于改进EMD和谱峭度法滚动轴承故障特征提取[J]. 振动、测试与诊断, 2013, 33(3): 478-482.

Zhang Zhigang, Shi Xiaohui, Shi Quan, et al. Fault feature extraction of rolling element bearing based on improved EMD and spectral kurtosis[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(3):478-482. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.01.005

*国家自然科学基金资助项目(51275524)

2015-01-14；

2015-04-16

TH322； TP306+.3

王余奎，男，1987年1月生，博士、讲师。主要研究方向为装备状态监测与故障预测。曾发表《Fault feature extraction of hydraulic pump based on CNC de-noising and HHT》(《Journal of Failure Analysis and Prevention》2015, Vol.15, No.1))等论文。 E-mail: wyktougao@163.com 通信作者简介：李洪儒，男，1963年1月生，教授、博士生导师。主要研究方向为信号处理技术、装备状态监测与故障预测、武器系统仿真。 E-mail: lihr168@sohu.com