三种柔性蒙皮支撑结构的力学特性*

沈 元， 朱 华， 刘卫东， 昂海松

(1.南京航空航天大学飞行器结构力学与控制教育部重点实验室 南京，210016)(2.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)(3.河海大学能源与电气学院 南京，211100)

三种柔性蒙皮支撑结构的力学特性*

沈 元1， 朱 华2， 刘卫东3， 昂海松2

(1.南京航空航天大学飞行器结构力学与控制教育部重点实验室 南京，210016)(2.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)(3.河海大学能源与电气学院 南京，211100)

理论推导了U型、V型和梯形3种柔性蒙皮支撑结构面内横向无量纲化弹性模量与其平面几何参数(壁厚系数t、高度系数h、形状系数k)之间的关系：其等效弹性模量随t增大而增大，随h增大而减小，随k增大而减小。采用ANSYS软件进行了有限元模拟并通过实验对其面内力学特性进行验证。同样参数条件下，3种结构面内横向刚度从大到小依次为V型、U型和梯形。说明梯形结构具有更强的变形能力，产生同样的变形需要的能量最小。对3种结构的面法向刚度进行了有限元仿真和实验比较，其面法向刚度随几何参数的变化规律与面内等效弹性模量相似；在相同等效面法向气动载荷作用下, 3种结构面法向位移大小依次为梯形、U型和V型。对3种结构拉伸前后不同载荷作用下的面法向最大位移进行实验测量，发现面法向刚度在拉伸后都有较大提升，在产生相同的面法向位移情况下，承受的压强平均提高了30%～60%。

变形机翼； 柔性蒙皮； 蜂窝结构； 弹性模量； 有限元分析； 面内拉伸； 法向变形

引 言

传统飞行器通常针对某种特定的飞行状态进行设计，在该飞行状态下能表现出较好的性能，而在其他飞行状态下性能则有所下降。随着飞行器设计研究经验的不断积累和其他学科技术的进步，为克服传统飞行器这种单任务模式的缺点，科学家们提出了变体飞行器的概念。变体飞机是指能够在飞行中改变气动外形,使飞机在不同飞行状态下性能保持最佳的飞行器[1]。机翼是飞机升力和操纵力的主要来源，是飞机设计的首要研究对象。相对于传统机翼，变形机翼能替代传统的铰链舵面，保证其气动外形的完整性，大大提高其气动性能。变形机翼要在飞行过程中进行变形，离不开柔性蒙皮[2-3]、变形作动器[4]及变形机构[5-8]等关键技术的支持。柔性蒙皮主要用于在变形时承受并传递气动载荷，保证机翼表面光滑，使机翼具有良好的气密性。

传统的固定翼或者刚性变体飞机采用的蒙皮都是刚性金属蒙皮，通常采用铝合金材料加工制造。在柔性变形机翼中，传统的蒙皮由于面内刚度太大，无法跟随机翼结构变形而变形。针对传统蒙皮的不足，科学家们已经提出了多种柔性蒙皮支撑结构，并对采用柔性材料制造的蒙皮样本进行了深入研究[9-11]。但是，由于材料性能的限制和变形机翼对柔性蒙皮的高要求，现有的蒙皮支撑结构还存在面内柔性与面法向刚性不足和制造工艺复杂等缺陷[12-14]，因此需要对蒙皮支撑结构进行深入设计与优化，开发出满足力学性能要求且易于加工制造的柔性蒙皮和相应的支撑结构。

蜂窝夹心结构具有结构轻、承载能力强和加工工艺成熟的特点，在飞机上越来越多地得到应用，因此采用蜂窝结构来支撑柔性蒙皮具有很高的可行性。国内外学者对此做了大量研究。文献[15-16]对零泊松比的六边形蜂窝和V型柔性蒙皮支撑结构的面内力学特性进行了研究，发现其面内刚度只有原始制备材料的0.1%～10%，并证明了柔性蒙皮在非变形方向被约束时，这两种结构的面内横向无量纲化等效弹性模量(结构的弹性模量与制备材料弹性模量的比值)均不会增加。 Bubert等[17]设计并制造了一种基于V型支撑结构的一维被动变形的柔性蒙皮，发现其在满足大变形条件下具有较好的承载能力。鲁超等[18]对V型零泊松比蜂窝芯斜壁板大变形条件下的弯曲变形和蜂窝芯横壁板小变形条件下的变形进行分析，证明其大变形方向上的等效弹性模量具有明显的非线性特征。这些研究仅仅是针对某种平面构型的蜂窝支撑结构进行分析，对不同构型支撑结构的面内和面法向特性缺乏系统性的比较，无法在实际应用中对结构的选用给出明确指导。

笔者选取3种不同构型的柔性蒙皮支撑结构作为研究对象：V型、U型和梯形。采用能量法对3种结构的横向无量纲化等效弹性模量理论模型进行了推导，并通过数值仿真与实验研究对该理论模型进行验证，最后利用数值仿真和实验研究对3种结构的面法向刚度进行探讨。

1 三种构型蜂窝支撑结构面内伸缩特性分析

1.1 理论模型推导

图1为不同构型柔性蒙皮支撑结构的平面示意图。图2为各构型蜂窝单元的参数定义和受力情况。每个单元长度为l，高度系数为h(即高度为hl)，壁厚系数为t(即壁厚为tl)，单元法向厚度为b，其中梯形结构单元形状参数比其他结构多一个即形状系数k。下面以V型结构为例对其进行力学分析。考虑到结构和载荷的对称性，取V型蜂窝的半单元结构进行研究，图3为V型结构的半单元结构示意图。点a固定，受拉力Fa和弯矩Ma作用；点b在拉力Fb和弯矩Mb作用下平移至点b′。为求取单元x方向的弹性模量，需要求得点b在x方向的位移δx。

根据图3，对V型结构半单元分段求解,由x方向平衡可得

Fa=Fb=Fc=Fx

(1)

假设Fa=Fb=Fc=Fx=F，根据力和力矩的平衡，从图4可以得出

M(x)+Ma=2Fhx

(2)

截面转角与弯矩的关系为

(3)

其中

(4)

转角边界条件为

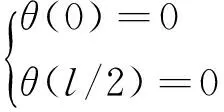
(5)

图1 3种构型柔性蒙皮支撑结构平面图Fig.1 Schematic plan of the three structures

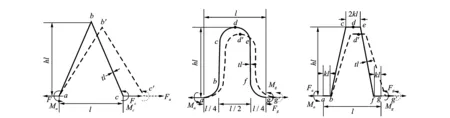
图2 不同构型蜂窝单元面内受力示意图Fig.2 In-plane force analysis of the celluar unit of the three structures

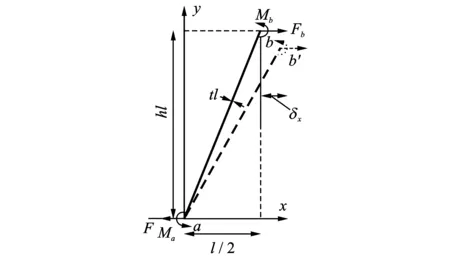
图3 V型结构的半单元结构受力示意图Fig.3 In-plane force analysis of half a unit of the V-type cellular

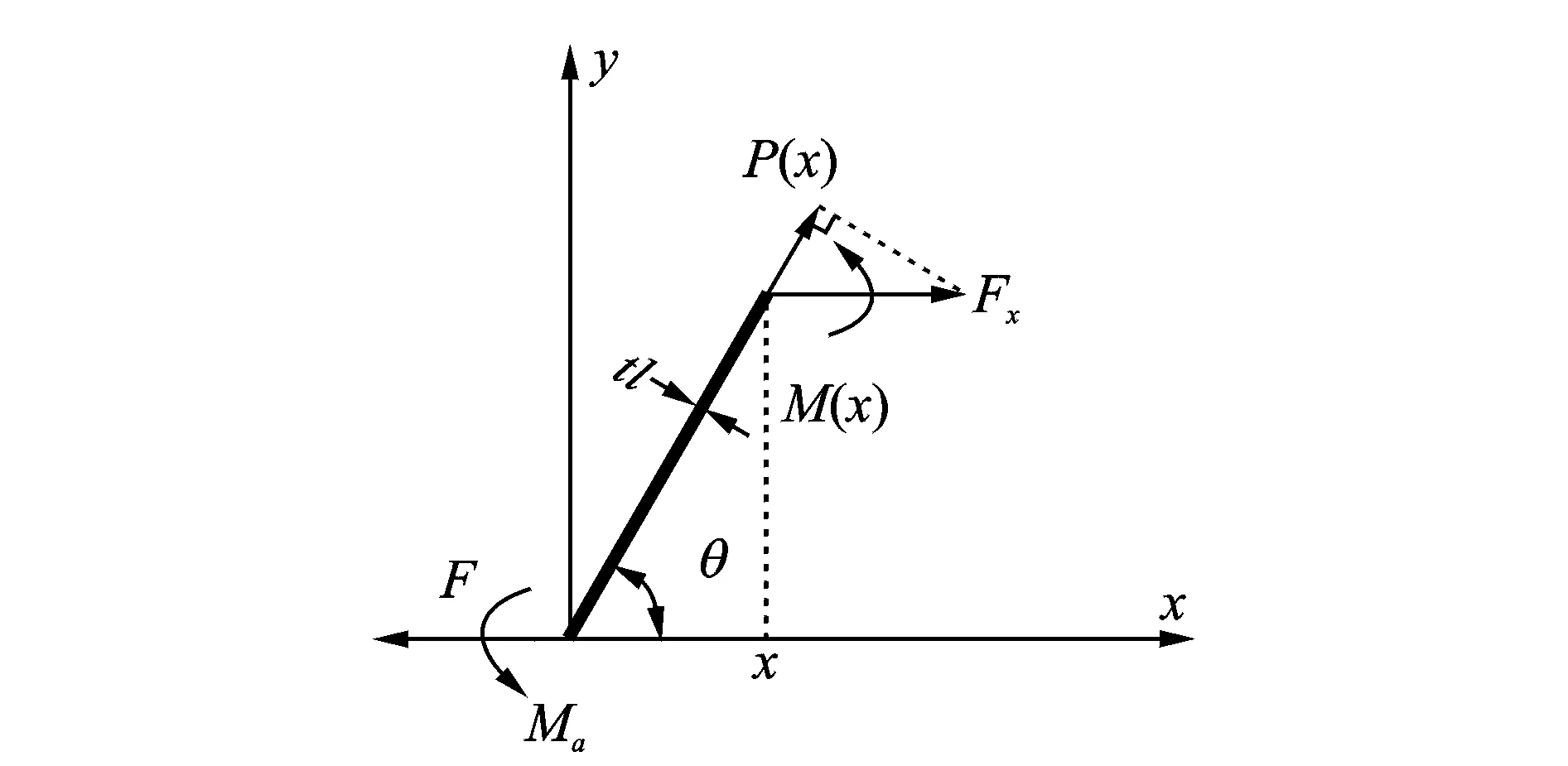
图4 V型结构的半单元0-x段结构受力分解Fig.4 Force decomposition of 0-x segment of half a unit of the V-type cellular

联立式(2)～(5)，求解得到

(6)

《F》状态内力弯矩为

(7)

《1》状态内力弯矩为

(8)

《F》状态轴力为

(9)

《1》状态轴力为

(10)

根据能量法有

(11)

将式(7)～(10)代入式(11)，积分得到

(12)

V型蜂窝支撑结构的面内横向等效应力和等效应变为

(13)

V型蜂窝支撑结构的面内横向无量纲化等效弹性模量为

(14)

其中：E为原材料的横向弹性模量。

采用同样方法可推导出U型结构的面内无量纲化等效弹性模量为

(15)

梯形结构的面内横向无量纲化等效弹性模量为

(16)

其中：k为形状系数，梯形结构需要3个参数描述。

1.2 基于ANSYS的有限元分析

利用ANSYS的参数化设计语言(ansysparametric design language，简称APDL)建立3种结构的参数化有限元模型，如图5所示。采用Solid45单元划分网格，弹性系数取为E=1.7 GPa(与实验采用的材料一致)，泊松比设为0.3。根据单元结构对称性采用半单元计算，半单元左端面固支，右端面施加位移载荷，通过有限元仿真得到半单元结构左端面的横向支反力，求得结构的面内横向无量纲化等效弹性模量。为方便与实验比较，有限元模型中统一取l=30 mm，法向厚度b=3 mm。对参数h，t和k等取多种组合进行计算，得到结构的面内横向无量纲化等效弹性模量与结构形状参数的关系。

图5 3种结构ANSYS半单元有限元模型Fig.5 FEM model of half a unit of the three structures in ANSYS

1.3 面内拉伸实验

实验材料选用厚度b=3 mm的POM板(聚甲醛板)，选取不同的形状参数进行组合(单元长度l均取30 mm)，对板材进行雕刻加工，得到所需的实验试件。力-位移测试设备采用微机控制电子万能试验机。图6为结构试件的加载实验示意图。

图6 V型、U型和梯形结构试件加载实验Fig.6 Loading experiment of the three types of the cellular structures

试件采用4×4的单元分布，固支边并列分布4个单元，每个单元高度为(h+t)l,试件横向总长度为4l(不计算纵梁宽度，因其不产生变形)。拉力测试仪所采集到的为每个样本对应的力-位移离散点，对数据进行线性拟合，由拟合直线的斜率求得结构的弹性模量Ex

(17)

其中：F为拉力；δl为样本在拉力F作用下产生的位移。

求得该结构的面内横向无量纲化等效弹性模量Exn=Ex/E，其中：Exnv，Exnu，Exnt分别为V型、U型和梯形结构的无量纲化等效弹性模量。

1.4 面内伸缩特性比较

1.4.1 面内伸缩特性算例和实验验证

如图7，8所示，V型结构面内横向无量纲等效模量随着t的增大而增大，随着h增大而减小。可以看出，理论推导、ANSYS数值仿真以及实验测试结果比较一致，进一步证实了理论模型的准确性。

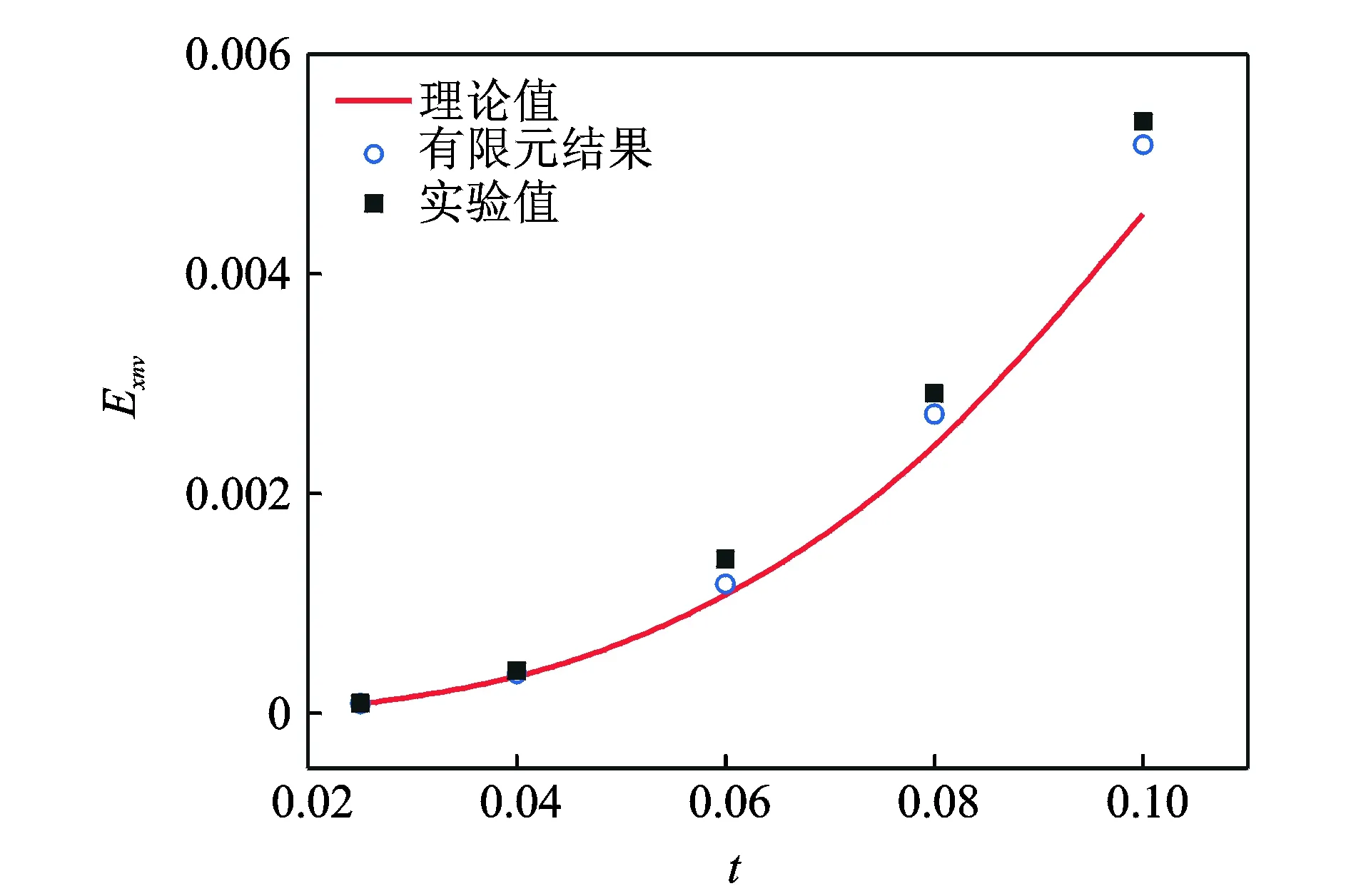
图7 Exnv随t的变化关系(V型结构) Fig.7 Exnv versus t(V-type)

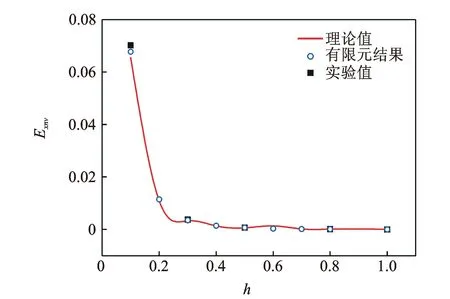
图8 Exnv随h的变化关系(V型结构)Fig.8 Exnv versus h (V-type)

1.4.2 3种结构面内伸缩特性比较

从图9(a)和图9(b)可以看出，3种结构的面内横向无量纲化等效弹性模量随着参数的变化趋势基本一致：随着高度系数h的增加而减小；随着壁厚系数t的增加而增加。在参数相同的情况下，结构的面内横向无量纲化等效弹性模量按照从大到小的顺利排列依次为V型、U型和梯形。该结果表明在相同尺寸参数条件下，V形结构在这3种结构中具有最差的面内伸缩特性；反之，梯形结构具有最佳的面内伸缩特性。在同样的变形需求下，梯形结构所消耗的变形能量最少。如图9(c)所示，由于梯形结构多一个参数k，其面内横向无量纲化等效弹性模量随着k增大而减小，意味着梯形结构的面内伸缩特性的可调节性更强。

图9 t,h,k分别对结构横向等效弹性模量Exn的影响比较Fig.9 Comparison of influence of t, h, k to dimensionless equivalent elastic modulus of the three structures (Exn versus t，h，k)

图10 ANSYS仿真:V型结构面法向加载情况Fig.10 ANSYS simulation: loading in normal direction (V-type)

2 3种构型蜂窝支撑结构面法向变形能力分析

2.1 基于ANSYS仿真的结构面法向刚度计算

由于蜂窝结构的面法向承载特性相比于面内伸缩变形更为复杂，因此采用有限元方法对其进行分析。利用ANSYS建立3种支撑结构的参数化模型和载荷分布。图10为V型结构面法向加载示意图。设定结构的边界条件为四周固支，载荷条件为面法向均布载荷。面法向仿真模型与面内拉伸实验试件尺寸一致，采用4×4的单元分布，横向两个单元间加有纵梁。在结构面法向加载中，纵梁作为结

构的一部分必须考虑在内，单个试件原始横向长度LT为4l加上3倍的纵梁宽度tl=2 mm，即LT=4l+3tl=126 mm。ANSYS仿真计算均在结构原长度下进行，纵梁长度统一取200 mm，不同参数结构的中心线在纵向位置保持一致。为与结构实际受载情况相统一，将相同面积(200×126 mm2)蒙皮所受面法向载荷平均分布到支撑结构上，即将支撑结构所受的面法向载荷等效为其支撑的蒙皮表面气动载荷。利用ANSYS求解在相同等效蒙皮气动载荷(Pe=200 Pa)作用下，结构的面法向最大位移Dn随其几何参数变化的情况。

图11为t,h,k对结构面法向最大位移的影响。如图11(a)所示，随着t的增大，3种结构的面法向最大位移逐渐减小，意味着结构的面法向刚度随着t增大而增大。如图11(b)所示，随着h的增大，3种结构的面法向最大位移同样增大，即结构的面法向刚度随着h增大而减小。如图11(c)所示，由于梯形结构多一个参数k，面法向最大位移随着k增大而增大，但增大比例不明显，说明k对面内刚度影响远远大于其对面法向刚度的影响。相同参数条件下(k>0.1)与面内刚度相似，面法向刚度从大到小依次为V型、U型和梯形。

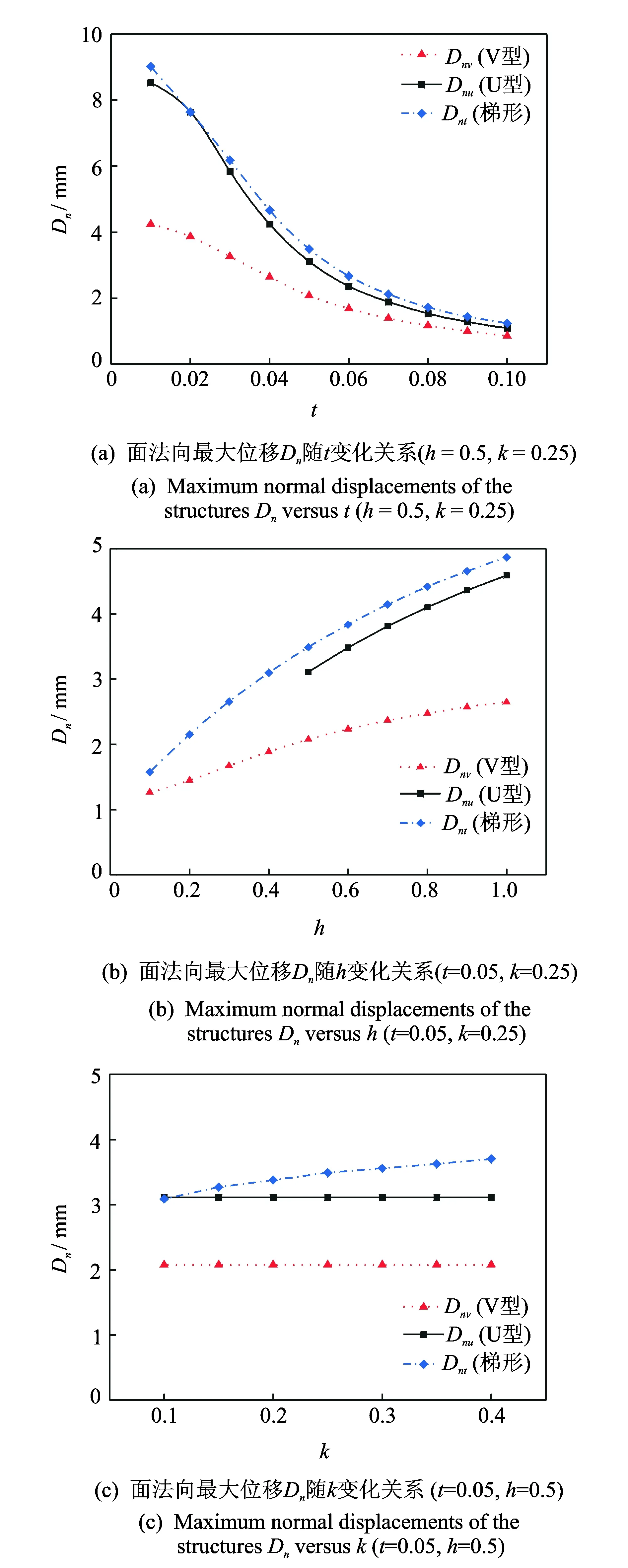
图11 t, h, k对结构面法向最大位移的影响Fig.11 Maximum normal displacements of the structures versus t, h and k

由以上分析可知，对于蒙皮支撑结构的面内伸缩变形能力较强的结构，其面法向承载能力较弱；而面法向承载能力较强的结构，其面内伸缩变形能力较弱。为解决这个矛盾，一方面，在选择合适的蒙皮支撑结构时，需要综合考虑机翼的变形驱动能力和飞行过程中蒙皮的负载情况。当机翼变形驱动能力较强或飞行过程中蒙皮负载较大时，可以考虑采用V型面内变形能力较弱但面法向承载能力较强的蒙皮支撑结构；反之，可以选择U型和梯形蒙皮支撑结构。另一方面，可以通过对结构进形进一步的参数优化，综合考虑机翼的变形驱动能力和飞行过程中的蒙皮负载，通过选择合理的结构形状参数，获得同时能够满足这两方面要求的蒙皮结构。

2.2 面法向加载实验

如图12所示，由于实验导轨宽度为160 mm，实验试件的纵向宽度取160 mm，沙箱宽度为150 mm，几何参数t=0.05，h=0.5，k=0.25。将结构试件的支撑座一端固定在平台上，另一端固定在滑块上。纵梁两端固支在导轨上。沙箱也设计成活动空间(可改变容积)，用激光测距仪测量试件中心处的面法向位移。试件表面铺上0.2 mm的硅胶蒙皮，其面法向刚度远远小于试件结构。由于激光测距仪精度仅为1 mm，实验过程中，通过不断加载直到激光测距仪读数发生改变，记录一次沙子的质量和试件中心的面法向位移。分别测量试件在原始长度(LT=126 mm)和119%长度(LT=150 mm)下中心点的位移随载荷的变化情况。针对3种结构的试件实际尺寸和约束情况重新进行ANSYS仿真，如图13所示。

图12 面法向实验设备、加载与测量Fig.12 Experimental equipment, loading and measurement

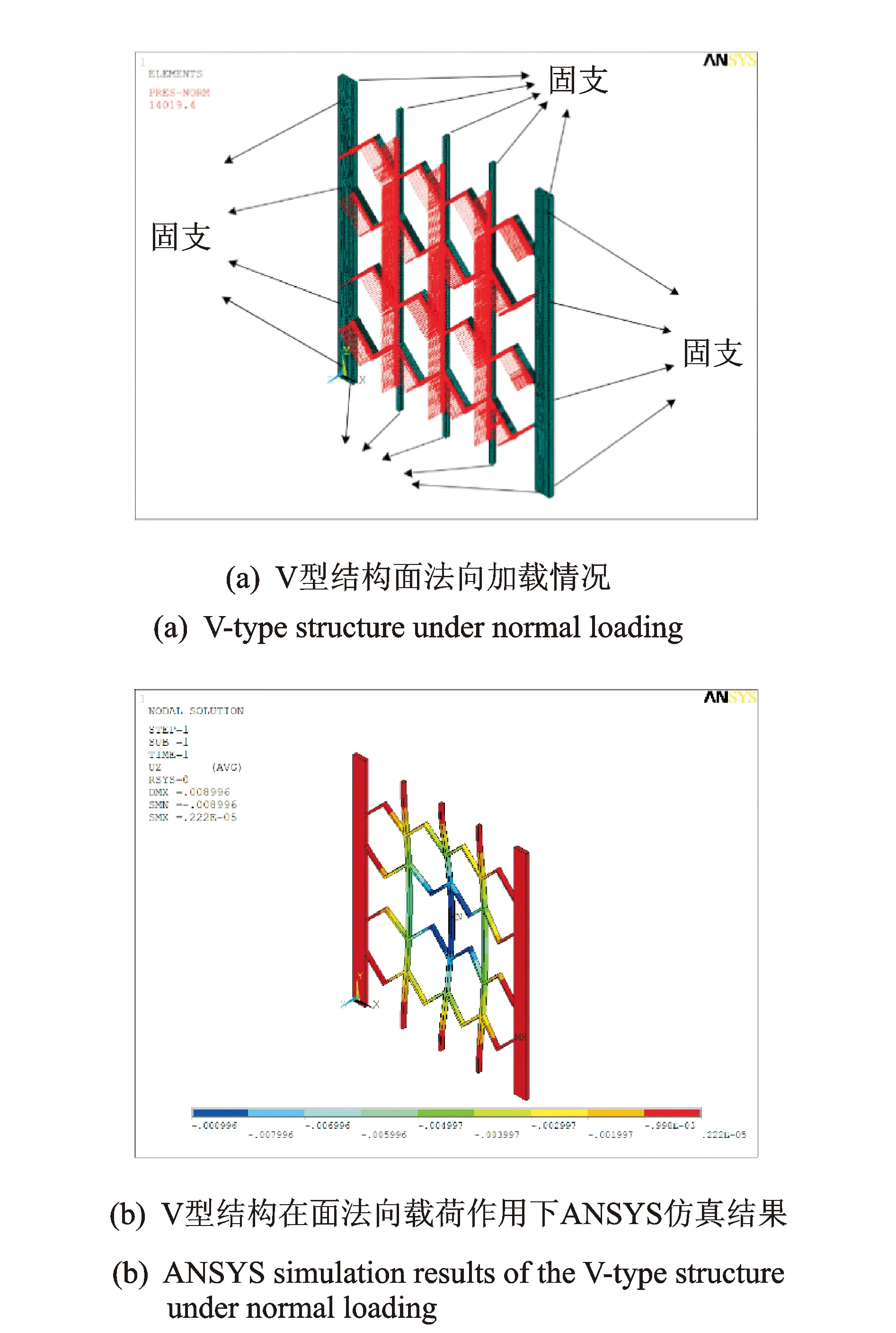
图13 与实验条件一致的ANSYS仿真(V型结构面法向受载情况和计算结果)Fig.13 ANSYS simulation consistent with the experiment(out of plane loading and calculation results of the V-type structure)

实验结果如图14所示，由于初始组装蒙皮和支撑结构时存在残余应力，使得支撑结构产生一定的法向变形，导致实验结果在初始阶段斜率较大，随着载荷的不断加大，3种支撑结构在实际面法向载荷下的变形趋势与ANSYS仿真结果逐渐接近，基本随蒙皮表面压强增大基本呈线性变化。图15为试件在原始长度(100%)和拉伸后长度(119%)下中心点的最大位移随载荷的变化比较。在同样参数条件下，面法向最大位移大小依次为梯形、U型和V型，说明面法向刚度大小依次为V型、U型和梯形，这与ANSYS仿真结果一致。值得注意的是，3种结构拉伸后的面法向刚度都有较大的提升。

图14 3种结构面法向最大位移实验值与有限元仿真结果比较Fig.14 Comparison of maximum normal displacements of the three structures between FEA and experimental results

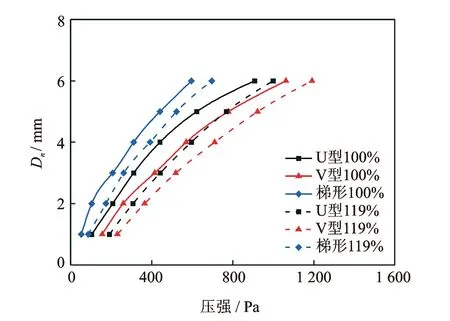
图15 3种结构拉伸前后面法向位移最大值比较Fig.15 Comparison of maximum normal displacements of the three structures before and after stretching

如表1所示，在产生单位法向位移变形下，承受的压强平均提高了30%～60%，且承受压强提升比例从高到低依次为梯形、U型和V型，这与未变形时面法向刚度大小排列相反。这说明面内变形能力较弱的结构形状在拉伸后面法向刚度的提升比例较大。

表1 面内拉伸前后蒙皮承受的平均表面压强比较

Tab.1 Average surface pressure of the flexible skin before and after stretching

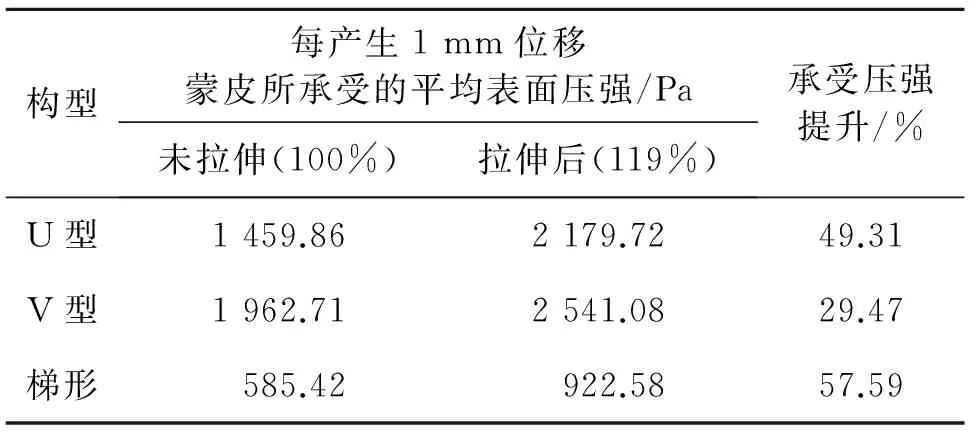
构型每产生1mm位移蒙皮所承受的平均表面压强/Pa未拉伸(100%)拉伸后(119%)承受压强提升/%U型1459.862179.7249.31V型1962.712541.0829.47梯形585.42922.5857.59

3 结 论

1) V型、U型和梯形3种柔性蒙皮支撑结构的面内横向无量纲化等效弹性模量随着壁厚系数t的增加而增加，随着h或k的增加而减小。

2) 同样参数条件下，面内横向弹性模量的大小依次为V型、U型和梯形。在同样的变形需求下，梯形结构所消耗的变形能量最少，其面内横向弹性模量变化区间最大，可选取的范围最广。

3) 3种结构的面法向刚度与3个参数(t，h，k)的关系与面内刚度类似。对于蒙皮支撑结构的面内伸缩变形能力较强的结构，其面法向承载能力较弱；而面法向承载能力较强的结构，其面内伸缩变形能力较弱。

4) 3种结构拉伸后的面法向刚度都有较大提升，在产生相同的面法向位移情况下，承受的压强平均提高了30%～60%，且面内变形能力较弱的结构形状在拉伸后面法向刚度的提升比例较大。

[1] Jha A K, Kudva J N. Morphing aircraft concepts, classification, and chanllenges[C]∥Proceedings of SPIE-Smart Structures and Materials 2004: Industrial and Commercial Application of Smart Structures Technologies. Bellingham:SPIE, 2004,5388:213-224.

[2] Thill C, Etches J, Bond I, et al. Morphing skins[J]. The Aeronautical Journal, 2008,112(1129):117-139.

[3] Thill C, Etches J A, Bond I P, et al. Composite corrugated structures for morphing wing skin applications[J]. Smart Materials and Structures, 2010,19(12):124009.

[4] Popov A V, Labib M, Fays J, et al. Closed-loop control simulations on a morphing wing[J]. Journal of Aircraft, 2008,45(5):1794-1803.

[5] Barbarino S, Bilgen O, Ajaj R M, et al. A review of morphing aircraft[J]. Journal of Intelligent Material Systems and Structures, 2011,22(9):823-877.

[6] Weisshaar T A. Morphing aircraft systems: historical perspectives and future challenges[J]. Journal of Aircraft, 2013,50(2):337-353.

[7] Sofla A Y N, Meguid S A, Tan K T, et al. Shape morphing of aircraft wing: status and challenges[J]. Materials and Design, 2010,31(3):1284-1292.

[8] Reich G W, Sanders B, Joo J J. Development of skins for morphing aircraft applications via topology optimization[J]. Journal of Intelligent Material Systems and Structures,2007,20:1-13.

[9] Popov A V, Grigorie T L, Botez R M, et al. Modeling and testing of a morphing wing in open-loop architecture[J]. Journal of Aircraft, 2010,47(3):917-923.

[10]Grigorie T L, Botez R M. New adaptive controller method for SMA hysteresis modelling of a morphing wing[J]. Aeronautical Journal, 2010,114(1151):1-13.

[11]Coutu D, Brailovski V, Terriault P. Promising benefits of an active-extrados morphing laminar wing[J]. Journal of Aircraft, 2009,46(2):730-731.

[12]Barbarino S, Ameduri S, Lecce L. Wing shape control through an SMA-based device[J]. Journal of Intelligent Material Systems and Structures, 2009,20(3):283-296.

[13]Mukherjee S, Ganguli R. A dragonfly inspired flapping wing actuated by electro active polymers[J]. Smart Structures and Systems, 2010,6(7):867-887.

[14]Bhandari B, Lee G, Ahn S. A review on IPMC material as actuators and sensors: fabrications, characteristics and applications[J]. International Journal of Precision Engineering and Manufacturing, 2012,13(1):141-163.

[15]Olympio K R, Gandhi F. Flexible skins for morphing aircraft using cellular honeycomb cores[J]. Journal of Intelligent Material Systems and Structures, 2010,21(17):1719-1735.

[16]Olympio K R, Gandhi F. Zero-ν cellular honeycomb flexible skins for one-dimensional wing morphing[C]∥48thAIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics,and Materials Conference. Honolulu,Hawaii: [s.n.],2007.

[17]Bubert E A, Woods B K S, Keejoo L, et al. Design and fabrication of a passive 1D morphing aircraft skin[J]. Journal of Intelligent Material Systems and Structures, 2010,21(17):1699-1717.

[18]鲁超,李永新,董二宝,等.零泊松比蜂窝等效弹性模量研究[J].材料工程,2013,12(15):80-84.

Lu Chao, Li Yongxin, Dong Erbao, et al. Equicalent elastic modulus of zero poisson′s ratio honeycomb core[J]. Journal of Materials Engineering, 2013,12(15):80-84. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.01.003

*国家自然科学基金资助项目(51605140)；江苏省自然科学基金资助项目(BK20150802)；中央高校基本科研业务费专项资金资助项目(2015B02914)

2015-01-13；

2015-04-24

TB332； TB214.6； TH140； TH122

沈元，男，1986年2月生，博士生。主要研究方向为飞行器设计和空气动力学。 E-mail: 297084462@qq.com 通信作者简介：朱华，男，1978年8月生，博士、副研究员。主要研究方向为机械设计及理论、超声电机技术和变体机翼技术。 E-mail：hzhu103@nuaa．edu．cn