TC4-DT钛合金材料动态力学性能及其本构模型

艾建光 姜 峰 言 兰

1.华侨大学制造工程研究院，厦门,3610212.华侨大学机电及自动化学院， 厦门,361021

TC4-DT钛合金材料动态力学性能及其本构模型

艾建光1姜 峰1言 兰2

1.华侨大学制造工程研究院，厦门,3610212.华侨大学机电及自动化学院， 厦门,361021

利用同步组装的高温分离式Hopkinson压杆试验装置，对TC4-DT钛合金材料分别进行了常温下不同应变率(930～9700 s-1)和应变率为5000 s-1时不同温度下(20～800 ℃)的动态力学性能测试，获得了各种冲击载荷下的应力-应变曲线。试验数据表明，TC4-DT材料具有应变率增塑效应且存在着临界应变率值，当应变率高于此值时应变率敏感性增强明显，此外随着材料加热温度的升高，软化效应减弱。利用试验所得的数据拟合了基于Power-Law和Johnson-Cook两种热-黏塑性本构方程且获得这两种动态本构模型参数，并将所得的两种拟合曲线与试验所得数据进行对比分析，结果表明两曲线吻合度都较好，此外还对这两种曲线的拟合精度进行对比，对比结果表明两种模型的拟合误差相差不大，但是Power-Law模型拟合精度要略优于Johnson-Cook模型的拟合精度。

TC4-DT钛合金；Johnson-Cook本构模型；Power-Law本构模型；应变率；分离式霍普金森压杆

0 引言

TC4-DT钛合金材料是我国近年来自主研发的一种新型中强高损伤容限型钛合金，该合金具有较高断裂韧度和抗疲劳裂纹扩展能力[1-2]。材料在实际的应用中难免会受到动态载荷作用，如高速冲击、切削加工等，而材料在动态载荷下的力学性能和静态载荷下表现出来的力学性能差别较大，国内一些学者在对无氧铜、奥氏体不锈钢、纯铁和TA7、TA11钛合金材料进行动态载荷测试时发现，这些材料具有较强的应变率增塑、增强和温度软化等效应,且在动态载荷下材料往往处于力-热效应耦合状态[3-6]。张长清等[7]在高应变率(1000～8000 s-1)下、LIU等[8]在低应变率(0.01～10 s-1)、不同温度(1181～1341 K)下对TC4-DT钛合金材料进行加载试验研究时，都发现TC4-DT钛合金材料具有应变率增强、增塑和温度软化等效应。如张正礼[9]利用Hopkinson测试技术分别对2024、7050、6061铝合金进行不同应变率下动态压缩实验，结果发现前两种型号铝合金对应变率不敏感，即随着应变率的升高，流动应力没有明显的升高，而后一种则出现了在高应率下表现出硬化的现象。

TC4-DT作为航空航天等领域所使用的材料，应具有优异的动态力学性能，使其在高速冲击载荷环境中，不会发生失效和断裂。因此，研究和建立TC4-DT钛合金在动态载荷下的力学性能及本构模型，对其在国内外各领域的广泛应用具有重要意义。本文中，笔者采用同步组装的高温分离式Hopkinson压杆装置对TC4-DT钛合金材料分别在室温、应变率为930～9700 s-1和应变率为5000 s-1、不同温度(20～800 ℃)条件下进行动态压缩试验。基于Power-Law模型(以下简称“P-L模型”)和Johnson-Cook模型(以下简称“J-C模型”)两种模型本构方程，并通过所得试验数据拟合得出了这两种本构模型的参数，两种拟合曲线与试验数据吻合都较好，此外还对比了这两种拟合曲线与试验数据的拟合精度，结果表明两种模型的拟合误差相差不大，P-L模型拟合精度好于改进J-C模型的拟合精度。

1 试验方案

1.1 试验材料及试样

本试验使用的材料是符合国家标准GB/T2965的钛合金冷轧棒材，其原始组织为网篮组织(图1)，具体化学成分见表1。由DAVIES等[10]提出的修正误差模型可知，当试样泊松比确定时，试样存在着最适宜的长径比可以让惯性效应引起的误差最小，故为了减小试样在高应变率试验中，由质点加速产生的纵向和径向惯性效应对试验数据的影响，并把试样与杆面积不匹配尽量降到最低，同时考虑本次试验设备的相关参数及应变率范围，本文试样取常用的试样长径比为1,本次试验两组试样的具体尺寸(D×L)为：5 mm×5 mm和2 mm×2 mm。同时为了满足分离式Hopkinson压杆(split Hopkinson pressure bar,SHPB)的应力均匀性假定和减小试验杆和试样端面摩擦效应[11]的影响，对试样两个端面进行了精加工，保证了两个端面具有较低的表面粗糙度(Ra≤0.8 μm)和平行度及与轴线的垂直度(≤0.01 mm)。

图1 TC4-DT钛合金的原始显微组织[7]Fig.1 Original Microstructure of TC4-DT Ti alloy

w(Ti)w(C)w(Al)w(H)w(V)w(O)w(Fe)w(H)Bal.0.046.160.0053.950.060.030.014

1.2 动态试验设备和试验原理

目前，在材料科学领域中研究材料在高应变率(102～104s-1)下的力学性能时，主要的研究方法就利用SHPB技术[12]。其试验原理是：将短试样置于两根压杆之间，通过加速的质量块撞击入射杆一端，以产生同时承担对试样加载和测试功能的应力波，同时利用粘贴在压杆上并距离杆端部一定距离的应变片来记录应力波传播信息求解杆件和试样端面的应力-位移-时间关系，其典型试验装置如图2所示。

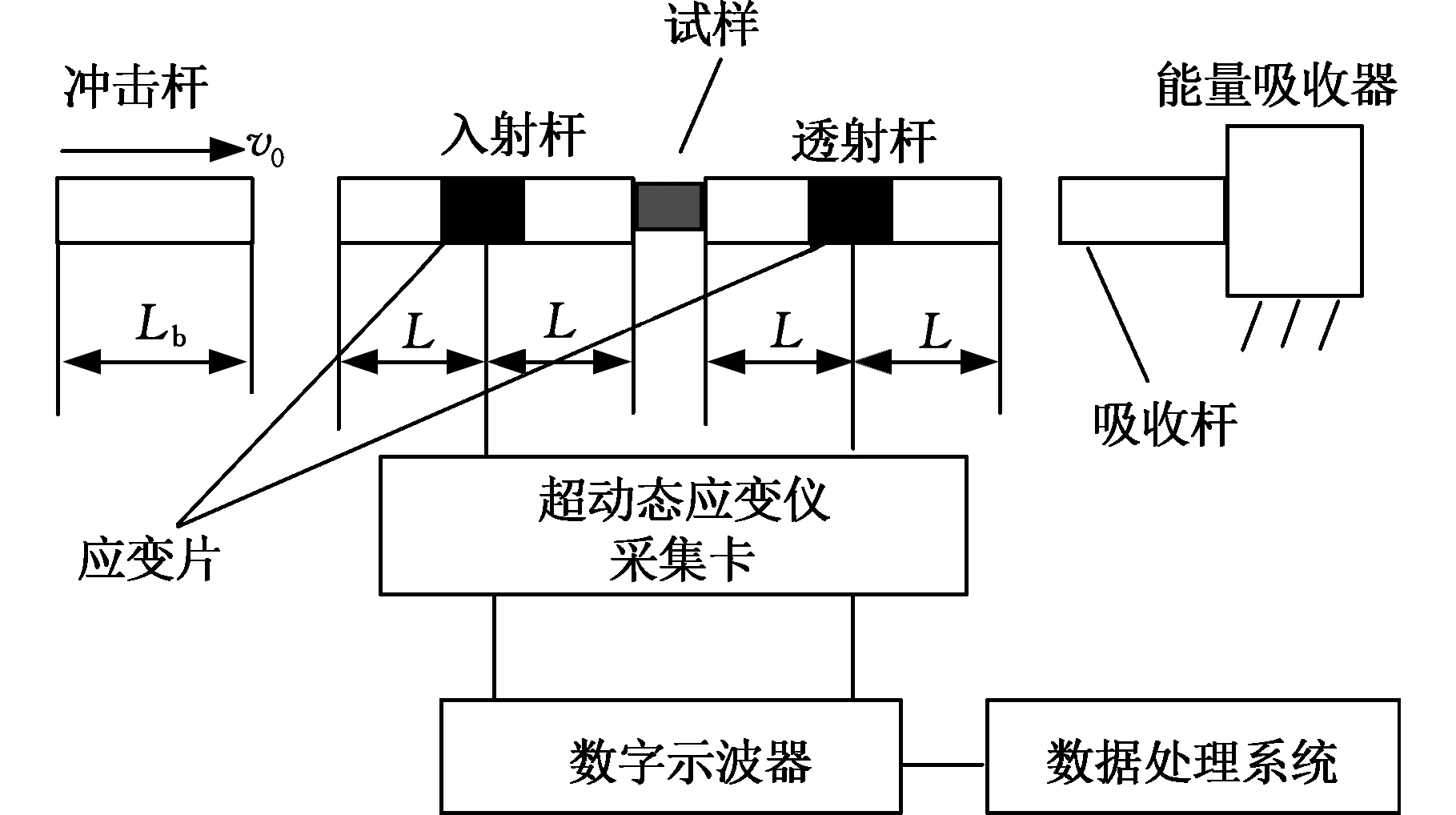
图2 分离式Hopkinson压杆试验装置简图Fig.2 Schematic split of Hopkinson pressure bar test

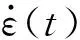
σ(t)=EAεt(t)/A0

(1)

(2)

(3)

C0=(E/ρ0)1/2

式中,E为杆的弹性模量;A0为杆的截面积;A为试样的截面积;C0为杆的一维弹性波速；ρ0为杆的密度;L0为试样的长度;εr为反射应变波幅值;εt为透射应变波幅值。

根据式(1)～式(3)可推导得到工程应力σe(t)、工程应变εe(t),它们与真实应力σT、真实应变εT之间满足以下关系：

σT=(1-εe(t))σεe(t)

(4)

εT=-ln(1-εεe(t))

(5)

利用Hopkinson压杆测得TC4-DT钛合金材料各杆中的原始波形，如图3所示。

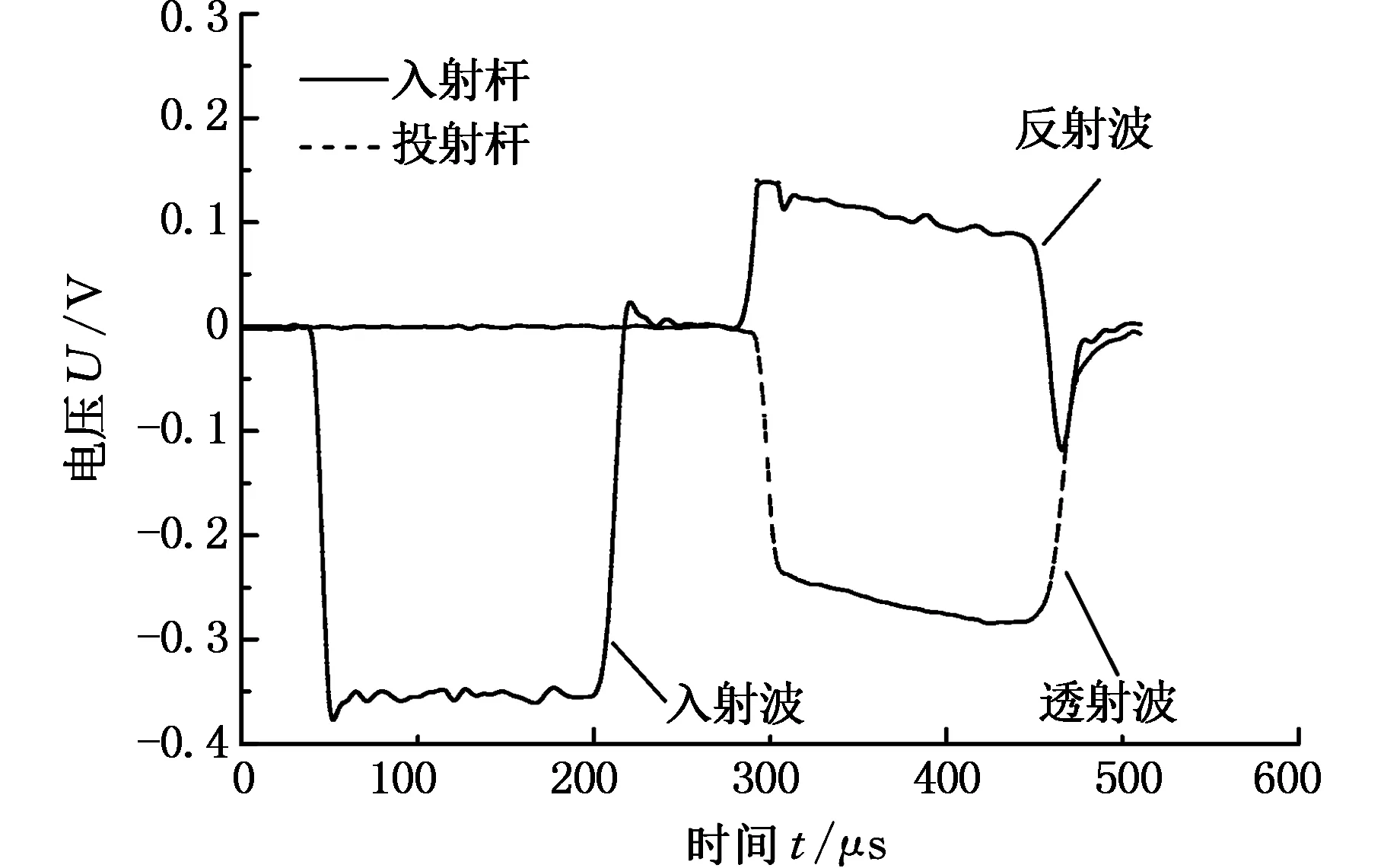
图3 入射杆和透射杆上的原始波形Fig.3 Original signal wave of in incident and transmitter bars

1.3 试验方案

试验设备为SHPB动态压缩装置，在温度为20 ℃下，当应变率为930 s-1和2650 s-1时,采用的压杆直径为D=13 mm，试样尺寸为D×L=5 mm×5 mm。而应变率为4800 s-1、6200 s-1、7100 s-1、9700 s-1时采用的压杆直径为D=5 mm，试样尺寸为D×L=2 mm×2 mm。在同一气压下，每组试验做4次，通过改变气压和试样尺寸的大小来获得不同应变率下的应力-应变曲线，之后取出每组数据中波形较可靠的反映材料真实力学性能的数据。本次试验需要对试样进行加热处理，而目前对试样加热的方法主要有两种：一种方法将试样直接夹在压杆之间进行直接加热，另一种方法是对试样加热到预期温度以后，再将试样夹在两杆之间。方法一虽然操作简单，但是不可避免地会在入射杆和投射杆中产生较大的温度梯度，而温度梯度会对试验数据产生较大影响。方法二主要是通过对SHPB装置进行设计，来使得加热试样尽可能地在压力脉冲到来之前缩短与压杆的接触时间，以缩小温度梯度场所影响的范围，减小温度梯度对试验数据的影响。本试验采用文献[13-15]提出的同步组装高温SHPB试验装置系统技术。其试验原理和设备装置在文献[16]中有详细的描述和说明。该加热系统采用环状可控直流电源加热炉，炉内温度误差±3 K,最高温度可达1473 K。

2 试验结果与分析

2.1 TC4-DT钛合金材料应变率敏感分析

图4所示为温度θ=20 ℃下，应变率为930 s-1、2650 s-1、4800 s-1、6200 s-1、7100 s-1、9700 s-1时测量的TC4-DT钛合金材料的真实应力-应变曲线，根据试验所得的数据，进行了真实应力应变率敏感性分析：真实应力随着应变的增大而非线性地增大，也被称为加工硬化，表明材料进入了塑性屈服阶段。材料的这种加工硬化特性归咎于塑性变形过程中的位错的增殖与交互作用。

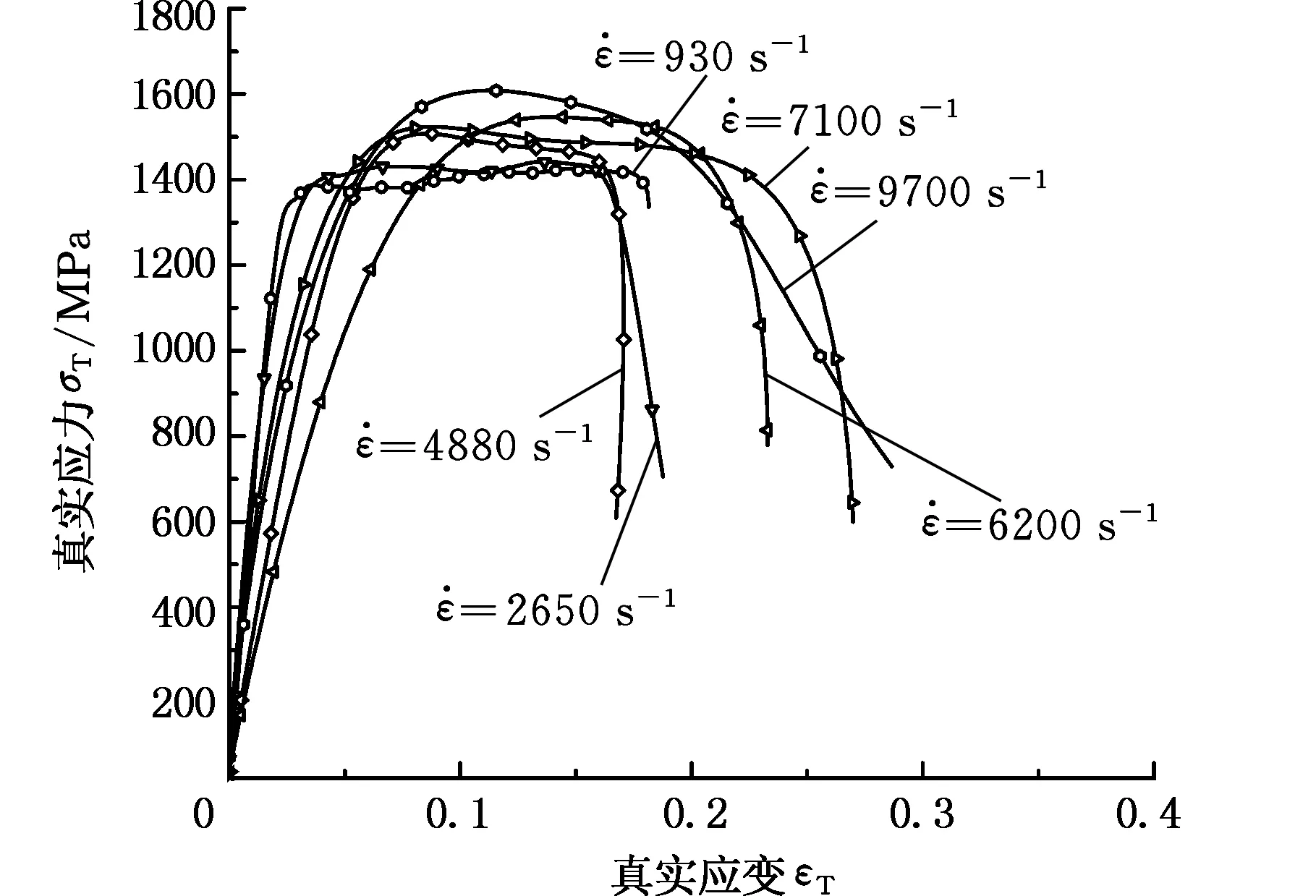
图4 常温下TC4-DT不同应变率下的真实应力-应变曲线(θ=20 ℃)Fig.4 True stress-strain curve of TC4-DT under different strain rates at room temperature(θ=20 ℃)

图5为应变为0.1，不同应变率下所对应的真实应力随应变率的变化曲线。由图5可知，TC4-DT钛合金具有较强的应变率敏感性，即材料的真实应力随着应变率的增大而显著增大。且在不同的应变率区间内，材料具有不同程度的应变率敏感性。在温度θ=20 ℃时，当应变率从930 s-1变化到4800 s-1，材料的真实应力从1356.59 MPa增大到1419.29 MPa；而当应变率从4800 s-1增大到9700 s-1时，材料的真实应力从1419.29 MPa增大到1603.58 MPa。

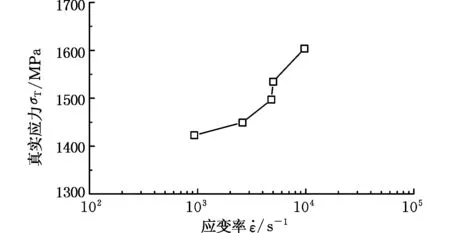
图5 常温下真实应力随应变率的变化(ε=0.1)Fig.5 Flow stress changes with strain rate at room temperature (ε=0.1)

图6 室温下不同应变率区间对材料应变率敏感性的影响(ε=0.1)Fig.6 True stress-strain curve of TC4-DT Ti alloy at room temperature(ε=0.1)

由图6可知，材料在应变率区间为4800～9700s-1时具有更高的应变率敏感性系数，罗皎等[17]认为产生这种结果的主要原因是材料在高应变率变形过程中的位错黏拽效应会显著增强。

当材料动态变形的应变率大于10s-1时，即可认为材料的变形过程为绝热过程。材料动态变形过程中的绝热温升可以通过以下公式进行计算：

(6)

式中，ρ为材料的密度；c为材料的质量热容；β为能量转换率(这里认为材料的塑性功全部转化为材料绝热温升，故取β=1)。

通过式(6)可计算得到理论最大温升，本次试验测试的材料TC4-DT钛合金的密度为4.5g/cm3，由梯形积分法可以求得绝热温升随应变的变化曲线。考虑到材料的质量热容受温度的影响比较大，试验采用质量热容测试仪装置对TC4-DT钛合金材料的质量热容进行分析，得出了材料的质量热容与温度数据并对其进行线性拟合，结果如图7所示。从图7中可以看出TC4-DT钛合金材料的质量热容随温度升高而增大。

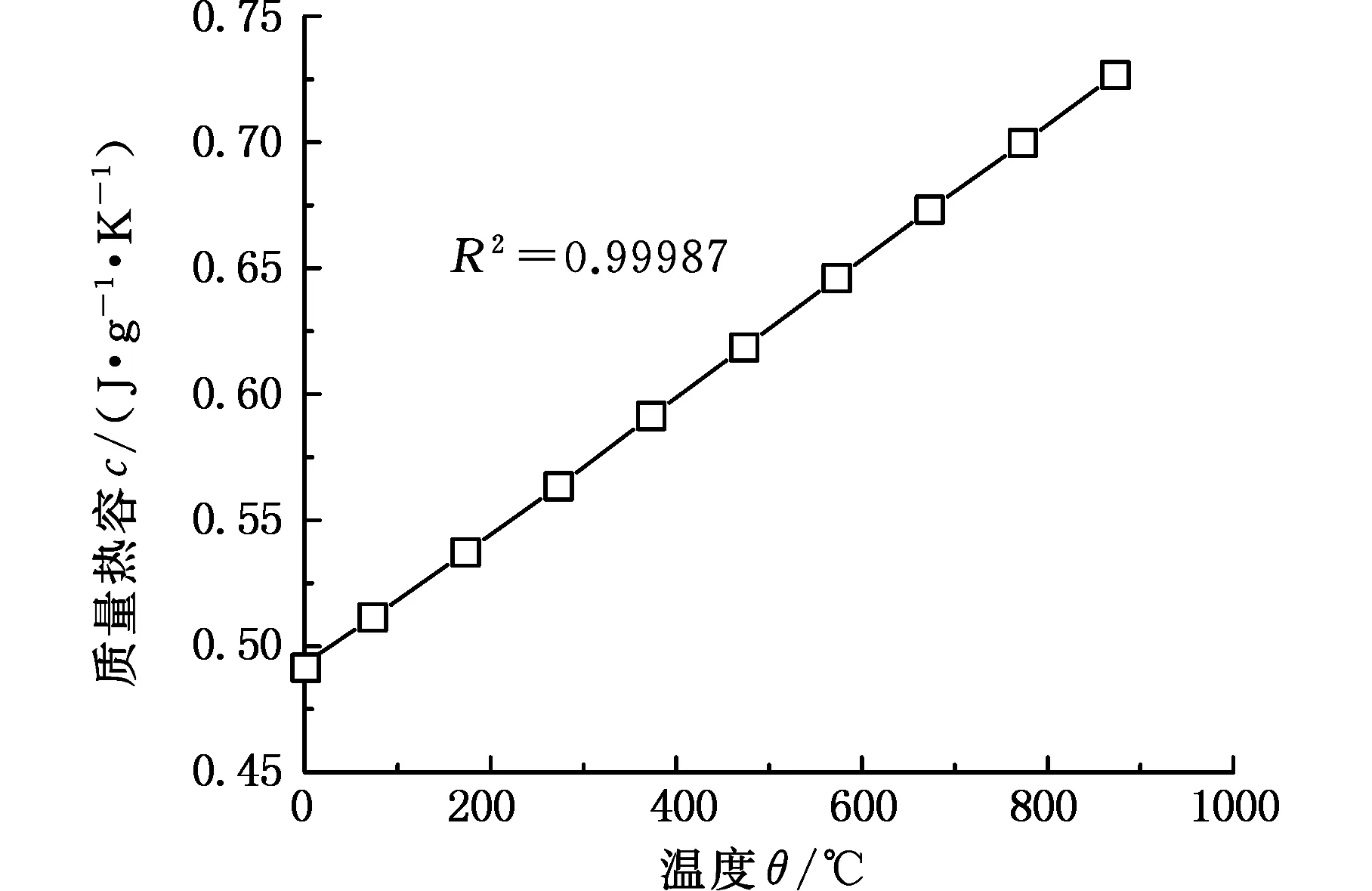
图7 TC4-DT钛合金材料的质量热容随温度变化情况Fig.7 Heat capacity of TC4-DT Ti alloys changes with temperature

按照式(6)和考虑绝热温升与质量热容存在耦合的关系，进一步计算得出了材料在变形过程中的绝热温升，图8给出了材料在应变率为5000s-1

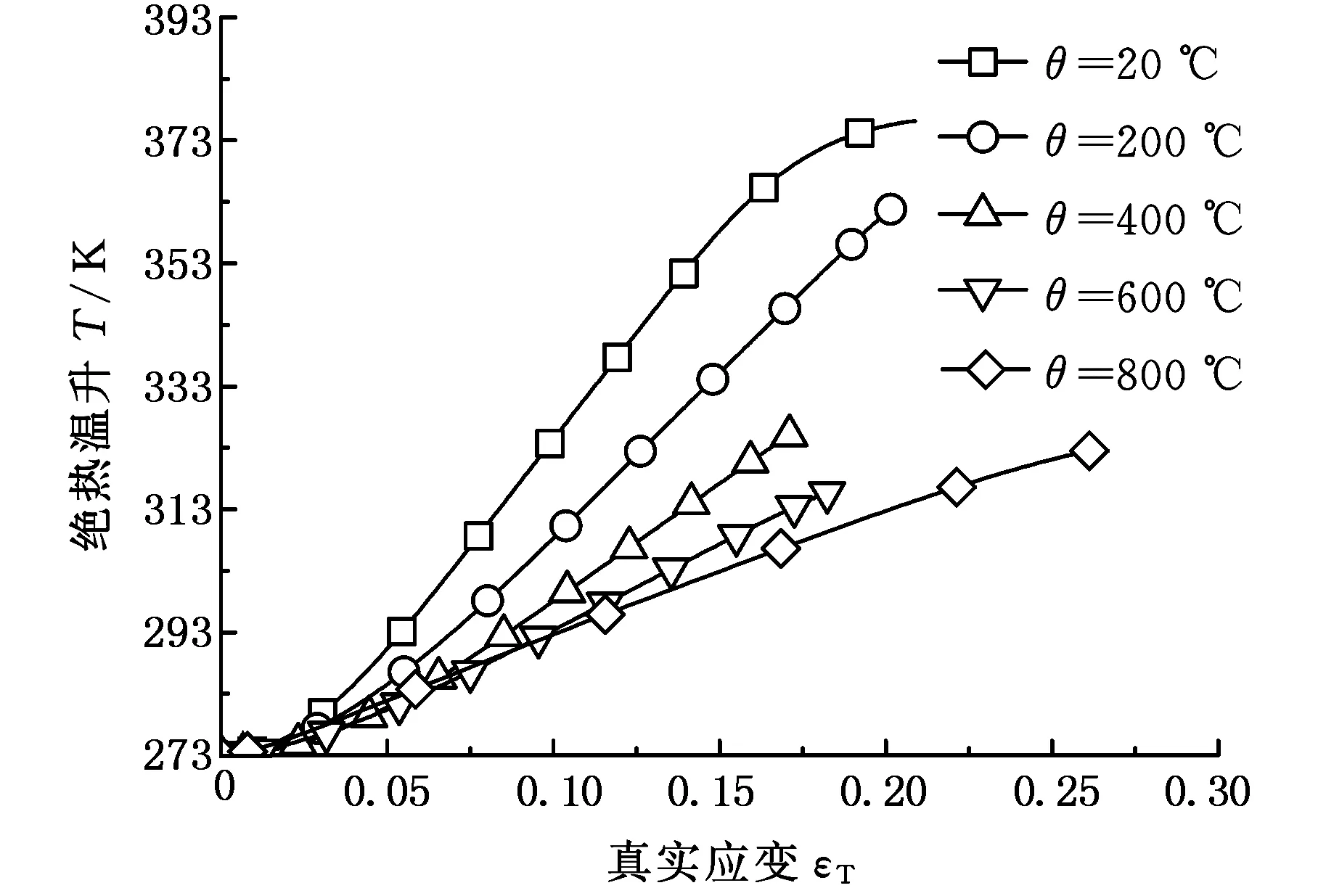
图8 应变率为5000 s-1时不同温度下的绝热温升Fig.8 Adiabatic temperature rise under different temperatures at strain rates 5000 s-1

时不同温度下的绝热温升。

由图8可知，当材料的温度在20～800 ℃之间时，采用多项式拟合方法，拟合出在20～800 ℃温度范围内TC4-DT材料的质量热容与温度关系的数学表达式为

Cp=0.48643+2.4433e-4θ+5.7556e-8θ2-3.6323e-11θ3

(7)

随着应变率的升高，相同冲击条件下，TC4-DT钛合金材料能达到的最大应变增大，真实应力增大，TC4-DT钛合金材料变形时总的塑性功增大，引起的绝热温升也显著增大。从图8可以看出，随着试样加热温度的上升，TC4-DT材料的绝热温升明显下降，这主要由于材料质量热容随温度升高而增大，而质量热容与绝热温升成反比所导致的。

2.2 TC4-DT钛合金材料的温度敏感性分析

图9所示为TC4-DT钛合金在5000 s-1应变率时不同温度下的真实应力-真实应变曲线，图10给出了应变率为5000 s-1和应变为0.12及不同温度下，TC4-DT材料的真实应力试样温度变化曲线，从图10中可以看出同一应变率和应变下真实应力随温度升高呈下降趋势，由图9可知，TC4-DT钛合金具有温度敏感性，即材料的真实应力随着温度的升高而降低，且随着温度升高，真实应力下降趋势减缓。同样，这里定义材料的温度敏感性系数为dσ/dθ， 图11给出了应变率为5000 s-1时温度区间为20～400 ℃和400～800 ℃时的温度敏感性系数。由图11可知，当温度区间由20～400 ℃变化到400～800 ℃时，材料的温度敏感性系数由1.47降低到0.96，这与图10给出的真实应力变化趋势一致。综上所述， TC4-DT钛合金在变形过程中具有应变率与温度敏感性，提高应变率或者降低变形温度使真实应力显著增大。

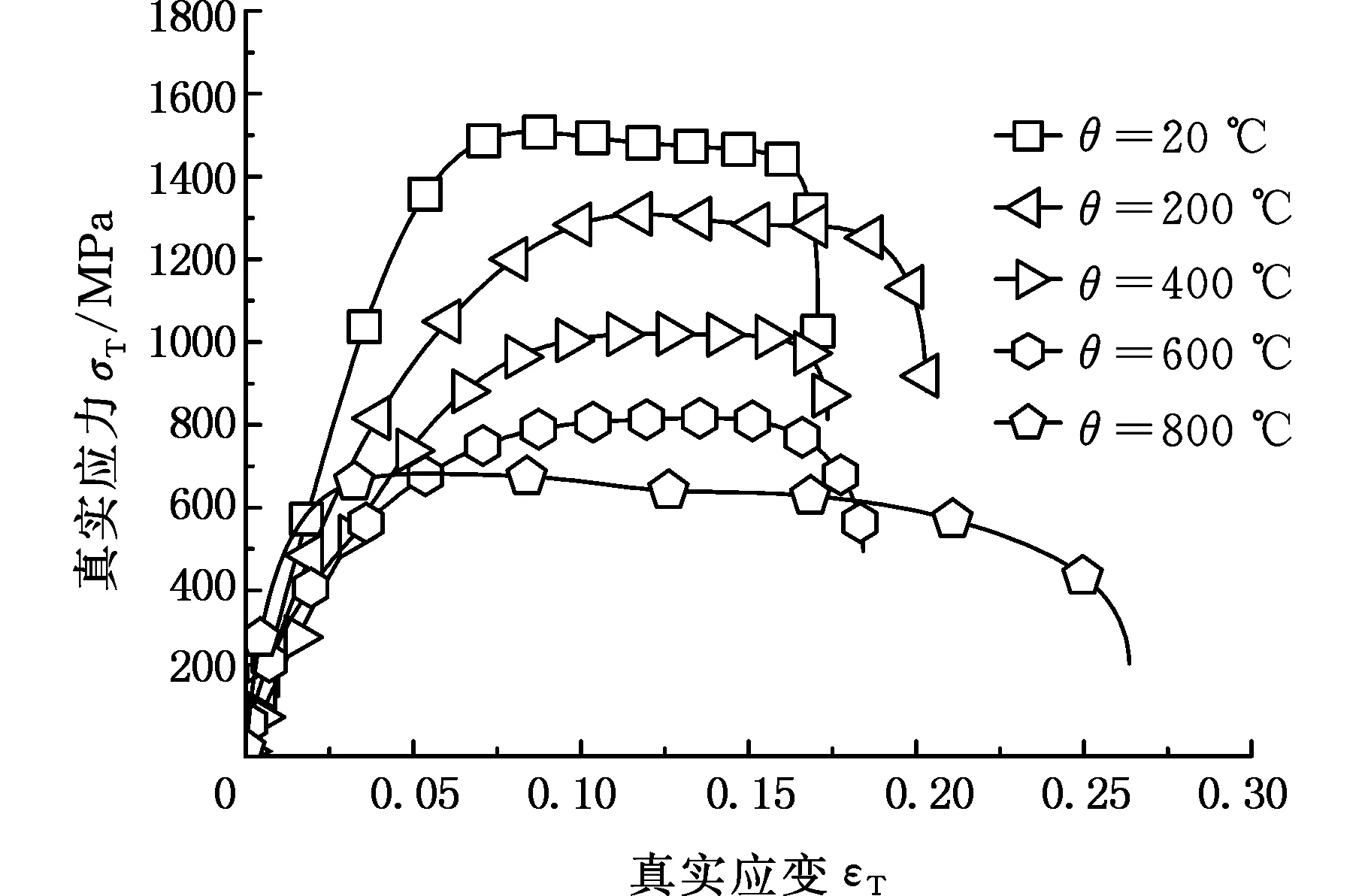
图9 TC4-DT钛合金不同温度下的真实应力-应变曲线 s-1)Fig.9 True stress-strain curve of TC4-DT Ti s-1)at different temperatures

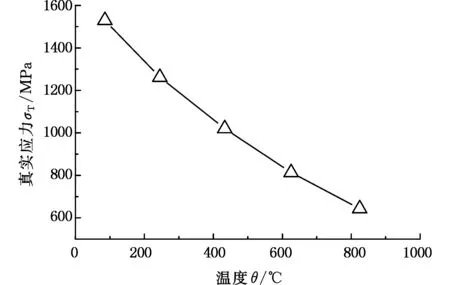
图10 5000 s-1应变率下真实应力随温度变化曲线(ε=0.12)Fig.10 Flow stress change with temperature at strain rate 5000 s-1 (ε=0.12)

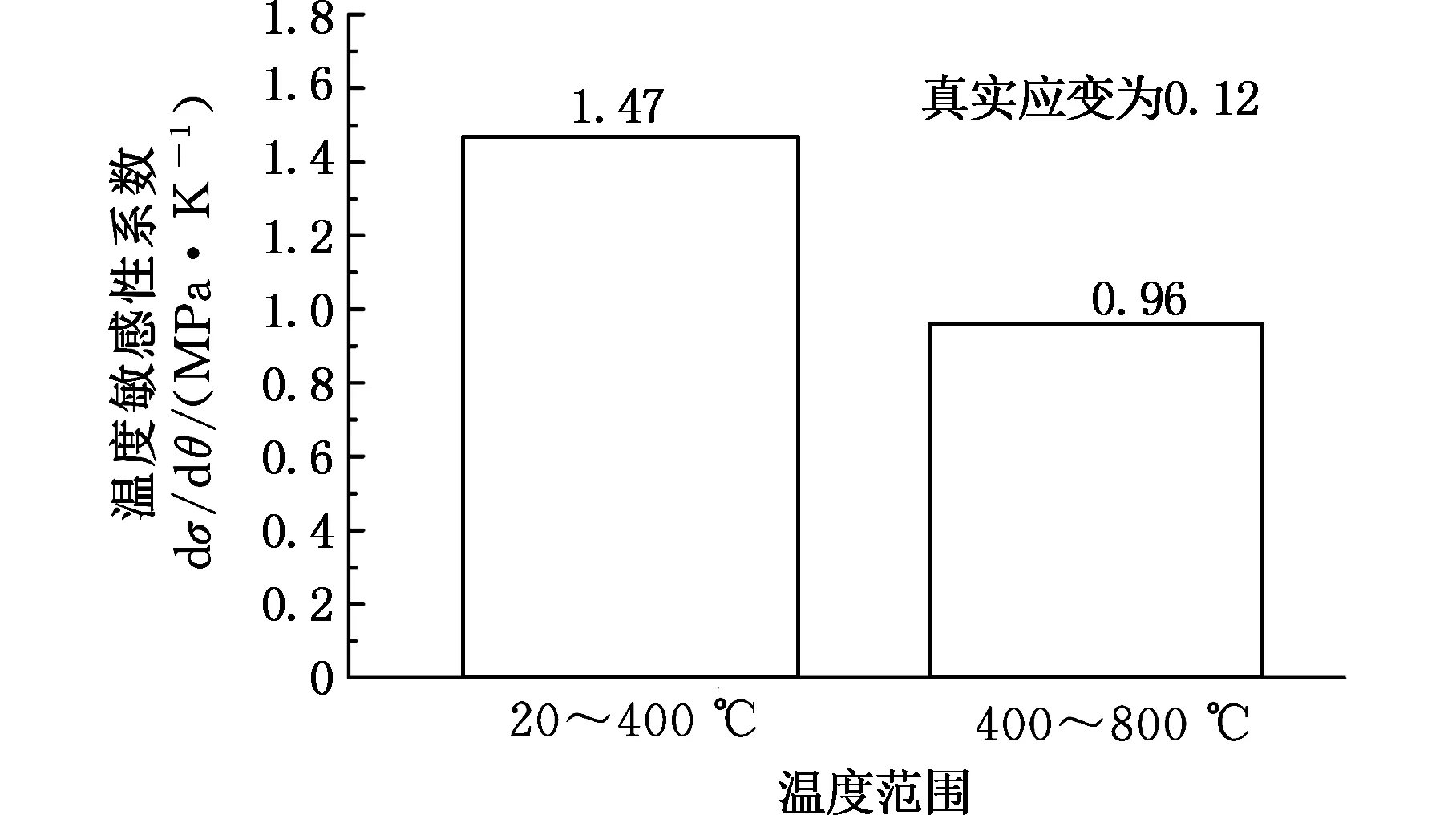
图11 应变率为5000 s-1不同温度区间对材料温度敏感性的影响 (εT=0.12)Fig.11 Influence of material temperature sensitivity on different range of temperature at strain rate 5000 s-1(εT=0.12)

3 TC4-DT钛合金材料本构方程的建立

目前，基于应力-应变曲线来描述金属材料本构模型有许多种，根据它们的主要形式，大致可以分为两种：一种是人工神经网络(ANN)模型[18]，另一种是分析模型，这种模型主要考虑的是材料的宏观现象和变形机制，这种模型给出了真实应力与变形参数(如温度、应变速率、应变)之间明确的关系，这种模型主要有：多项式本构模型[19]、改进Arrheniu模型[20]，J-C模型[21]、Zerrilli-Armstrong模型[22]、P-L模型[23]等。而J-C模型和P-L模型都是经验型的黏塑性本构模型，其形式都比较简单，而且都表达了应力与应变、应变率及温度之间的关系，因此在工程领域得到广泛运用。故本次试验选择J-C 模型和P-L模型这两种模型作为TC4-DT钛合金材料的本构模型。

3.1 基于Power-Law本构模型的TC4-DT钛合金材料本构方程参数

通过对试验数据的回归分析，拟合出基于P-L关系的本构模型的材料参数。本构模型的表达式如下[6]：

(8)

(9)

(10)

Θ(T)=C0+C1T+C2T2+C3T3+C4T4+C5T5

(11)

T=Tin+ΔT

(12)

(13)

材料参数σ0是通过对常温下最低应变率时的应力-应变曲线(即图4中对应的930 s-1曲线)在低应变区对应的曲线进行线性拟合得出弹性区与塑性区的大致转变点，从曲线上读出材料参数σ0为1356.59 MPa。取参考应变为0.02，并对式(13)两边同时取对数，可得

(14)

将应变为0.03～0.15对应的真实应力值以及相应的应变代入式(14)，并通过最小二乘法线性拟合得到直线斜率(1/n)为0.0287，进一步求得材料参数n为34.843 21，如图12所示。使用θ=20 ℃、应变率范围为930～9700 s-1材料真实应力-应变曲线来确定材料参数m，当材料在常温变形时，假设材料的温度软化项为1。因此，本构模型可以简化为

(15)

将式(15)两边同时取对数，可得

(16)

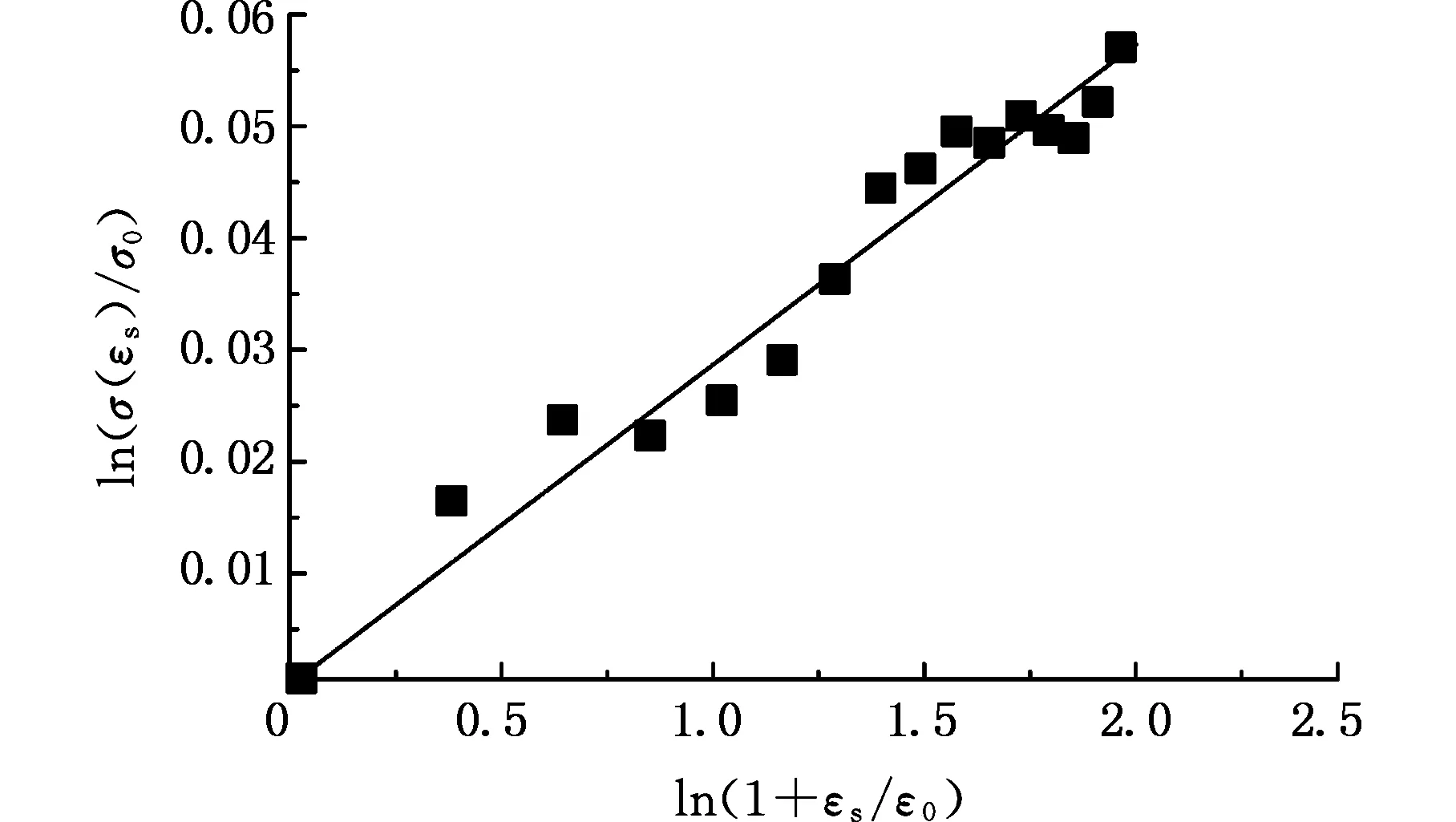
图12 ln(σ(εs)/σ0)和ln(1+εs/ε0)的关系Fig.12 Relationship between ln(σ(εs)/σ0) and ln(1+εs/ε0)

此处取参考应变率为9000 s-1。由于材料在小应变时绝热温升较小，所以应变软化效应不明显。因此取应变为0.02时对应的真实应力以及相应的应变率代入式(16)，并通过最小二乘法线性拟合得到直线斜率(1/m)为0.1255，进一步求得材料参数m=7.968 13，如图13所示。使用应变率范围为930～9700 s-1、温度范围为20～800 ℃的应力-应变曲线来确定材料参数C0～C3，本构模型变为

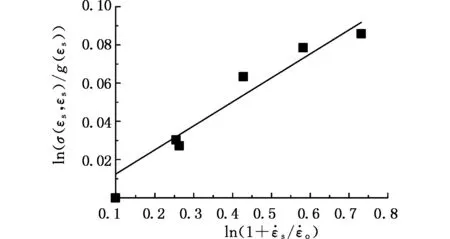
图和ln(1+) 的关系Fig.13 Relationship between ln σ(εs,)/g(εs) and ln(1+)

(17)

将不同温度下的真实应力代入式(17)，并通过多项式拟合可得材料参数C0～C3分别为：1.097 07，-1.130 03×10-3，2.248 41×10-7，2.015 18×10-10。拟合曲线如图14所示。根据上述步骤确定了各材料参数后，则用于描述TC4-DT钛合金材料的本构模型可以表达为

(18)

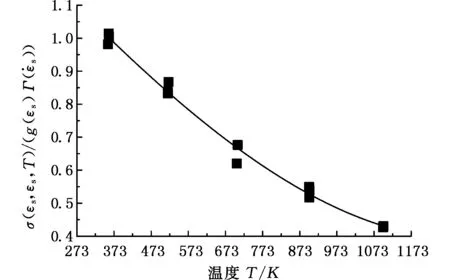
图和温度的关系Fig.14 Relationship between σ(εs,,T)/(g(εs)·

3.2 基于J-C本构模型的TC4-DT钛合金材料本构方程参数

本次试验选择J-C模型作为TC4-DT钛合金的本构模型，用来和上面选用的P-L模型进行比较，J-C模型的一般形式为[18]

(19)

T*=(T-Tr)/(Tm-Tr)

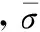
首先，J-C本构方程中等式右边第一项对应于室温及应变率，本构模型成为如下表达式：

(20)

根据材料的常温准静态压缩试验确定材料的加工硬化常数，由图4可知，材料的初始屈服强度为1356.597 MPa(这里即为A的值)，取参考应变为0.03。根据式(20)，将参数A移项可得

(21)

对式(21)两边同时取对数可得

(22)

所以，拟合得到的曲线斜率即为n，得到n=0.054 09,如图15所示。

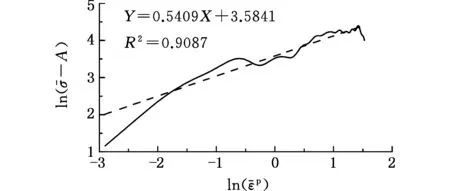
图15 J-C模型第一项拟合曲线Fig.15 J-C model first fitting curve

根据公式

(23)

可得

(24)

对曲线进行线性拟合，可得C=0.039 20，如图16所示。最后根据公式：

(25)

将式(25)两边取对数，整理可得

(26)

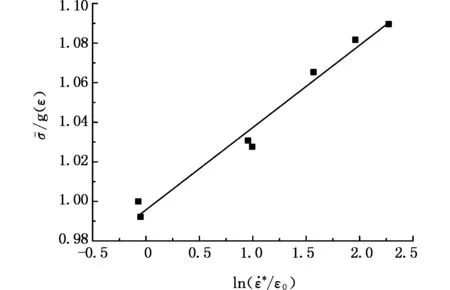
图16 J-C模型第二项拟合曲线Fig.16 J-C second model fitting curve

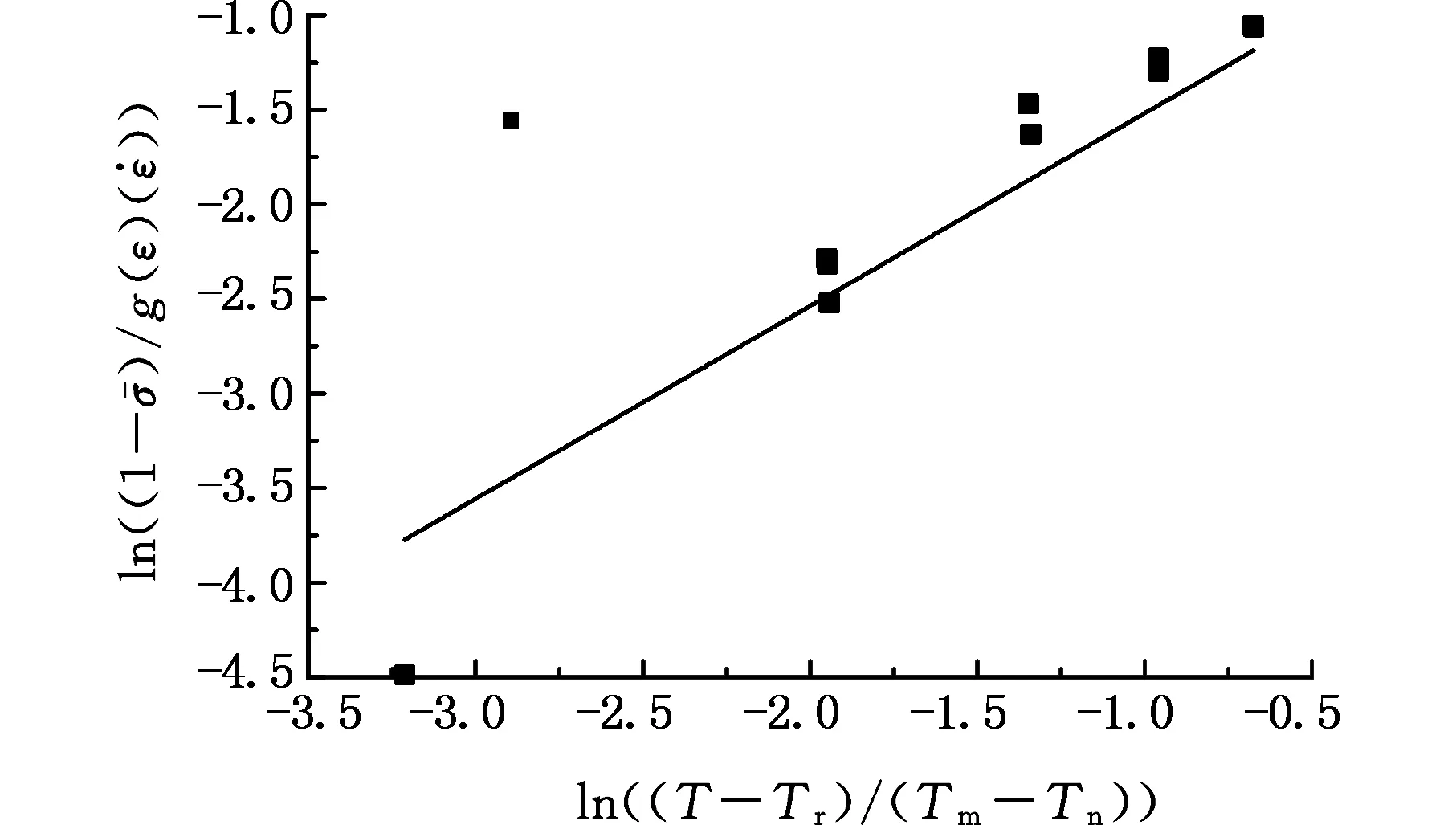
图17 J-C模型第三项拟合曲线Fig.17 J-C third model fitting curve

最后，根据不同温度的动态变形曲线确定材料的温度软化项参数m的值。所以由图17可得：应变率为5000 s-1时，m=1.0188；根据上述的计算结果，得到TC4-DT钛合金的J-C本构方程为

(27)

3.3 模型拟合曲线与试验结果的比较

将获得的基于P-L本构模型和J-C本构模型的TC4-DT钛合金材料本构方程拟合结果与试验结果进行比较，图18～图23为不同应变率下模型曲线和试验结果对比图，图24是应变率为5000 s-1不同温度下模型曲线与试验结果比较。通过比较可以看出，建立的两种本构方程可以较好地反映材料的动态力学性能变化，并且比较了两种模型的拟合精度相对误差，如表2和表3所示，由表2和表3可以看出P-L本构模型和J-C本构模型的拟合误差相差不大，P-L模型拟合精度更高一点。由于在上述两种模型中，前两项表达式中都是以指数形式表示，差异性不大。而唯一存在较大差异的就是表达式最后一项，即

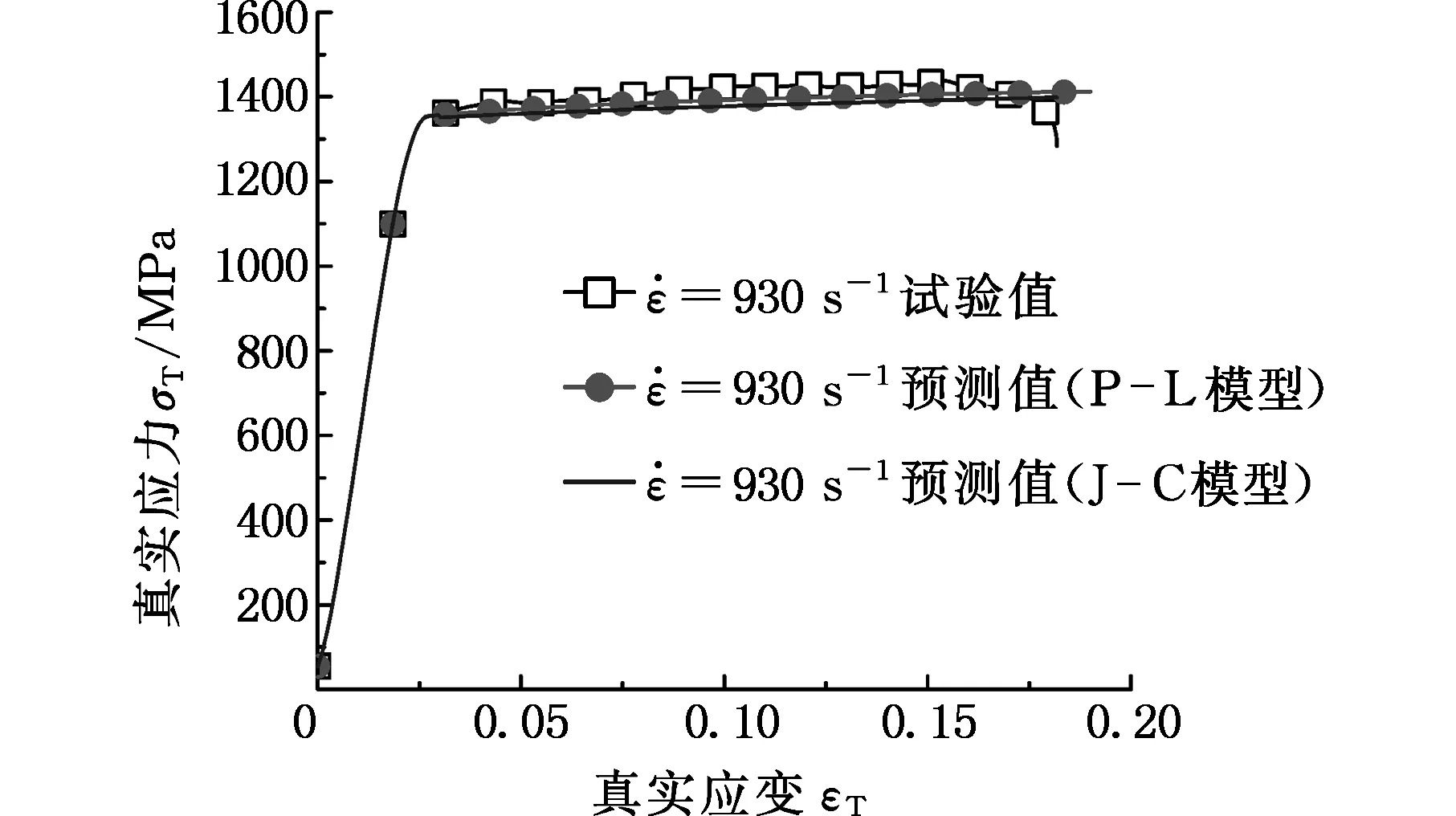
图18 模型曲线和试验结果对比 s-1)Fig.18 Comparison of model curves and test results at strain rate 930 s-1

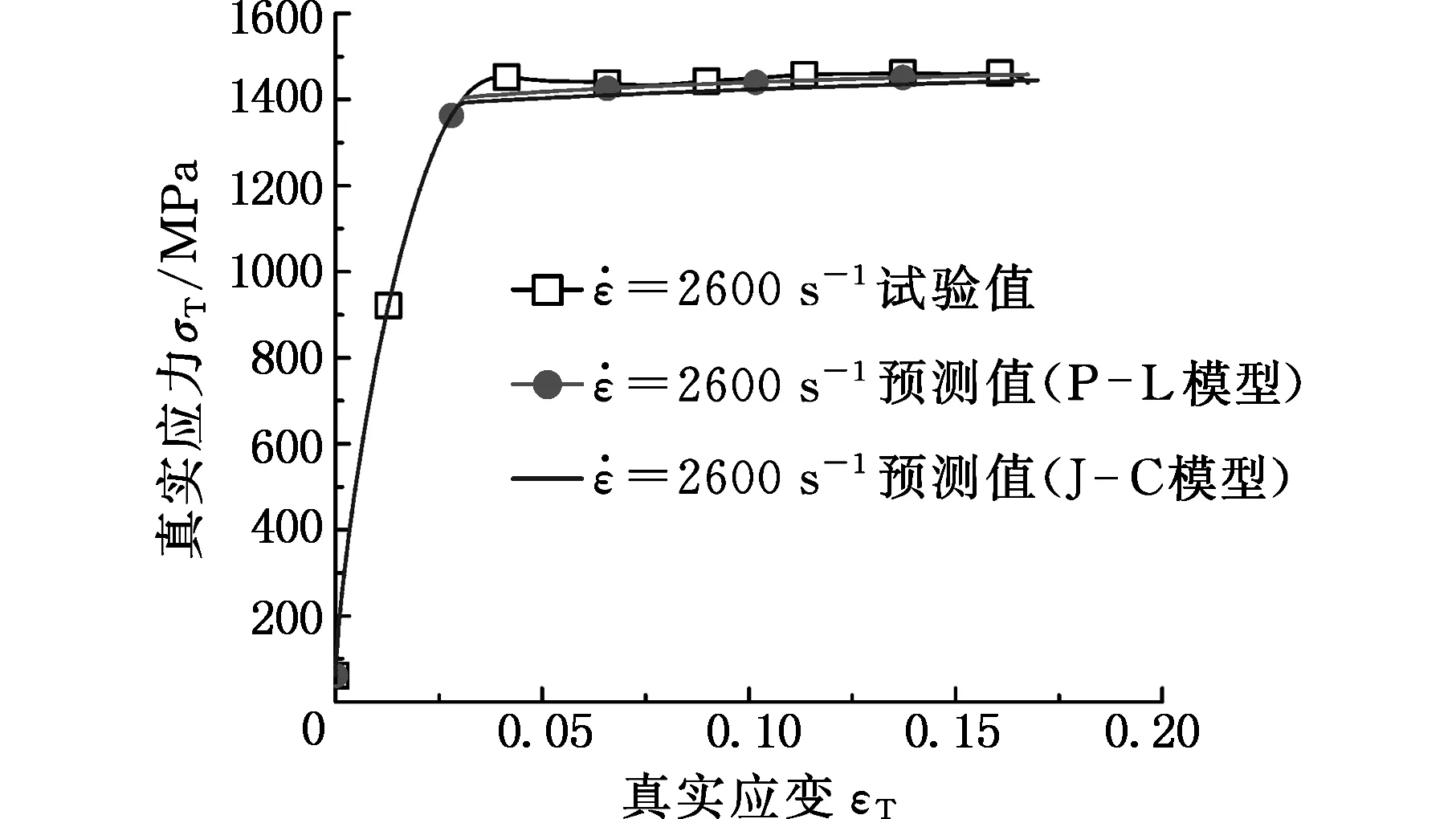
图19 模型曲线和试验结果对比 s-1)Fig.19 Comparison of model curves and test results at strain rate 2600 s-1

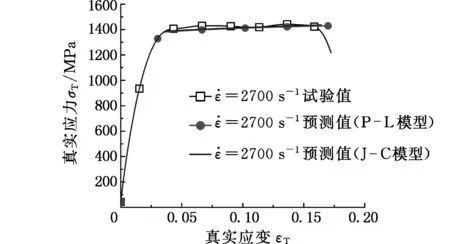
图20 模型曲线和试验结果对比 s-1)Fig.20 Comparison of model curves and test results at strain rate 2700 s-1

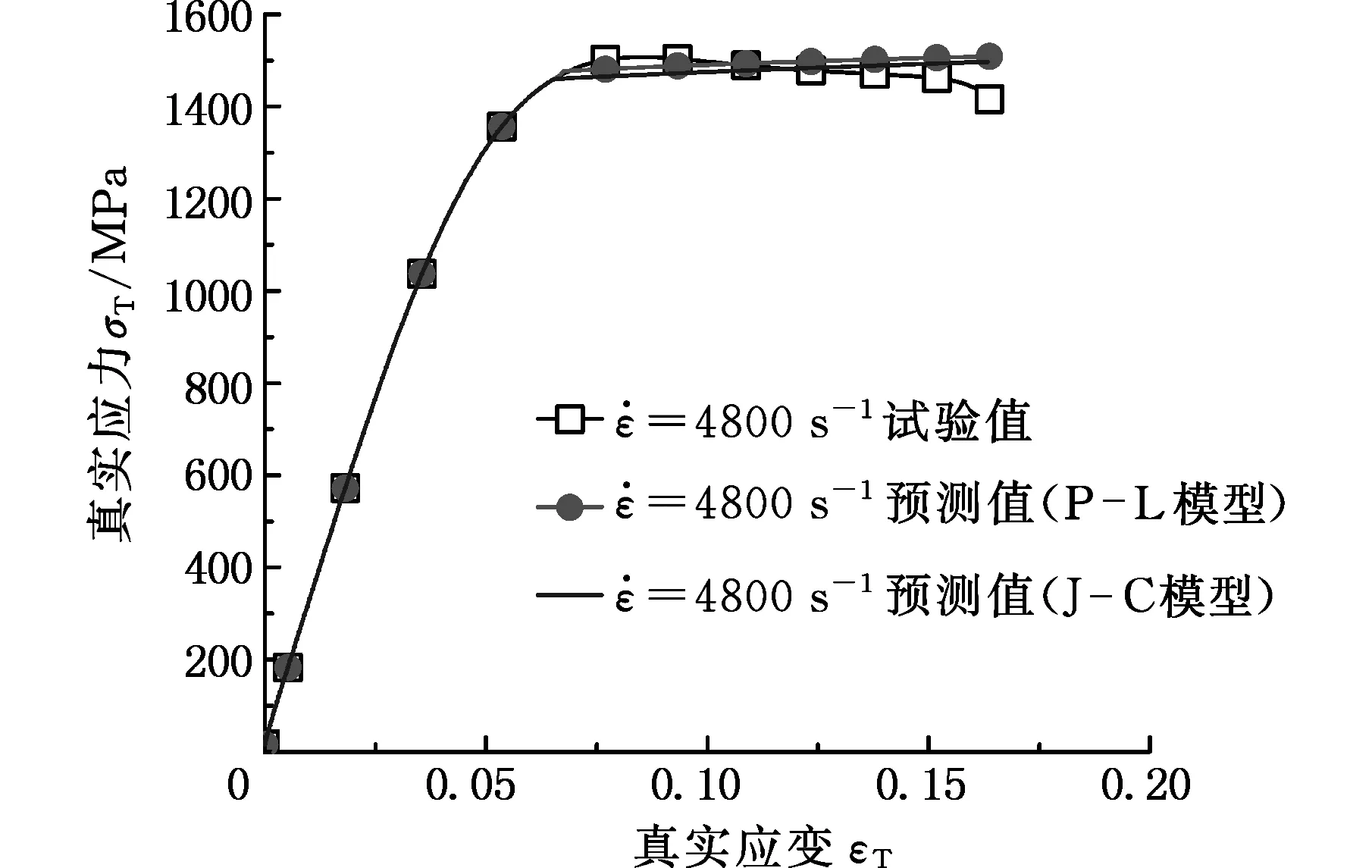
图21 模型曲线和试验结果对比 s-1)Fig.21 Comparison of model curves and test results at strain rate 4800 s-1

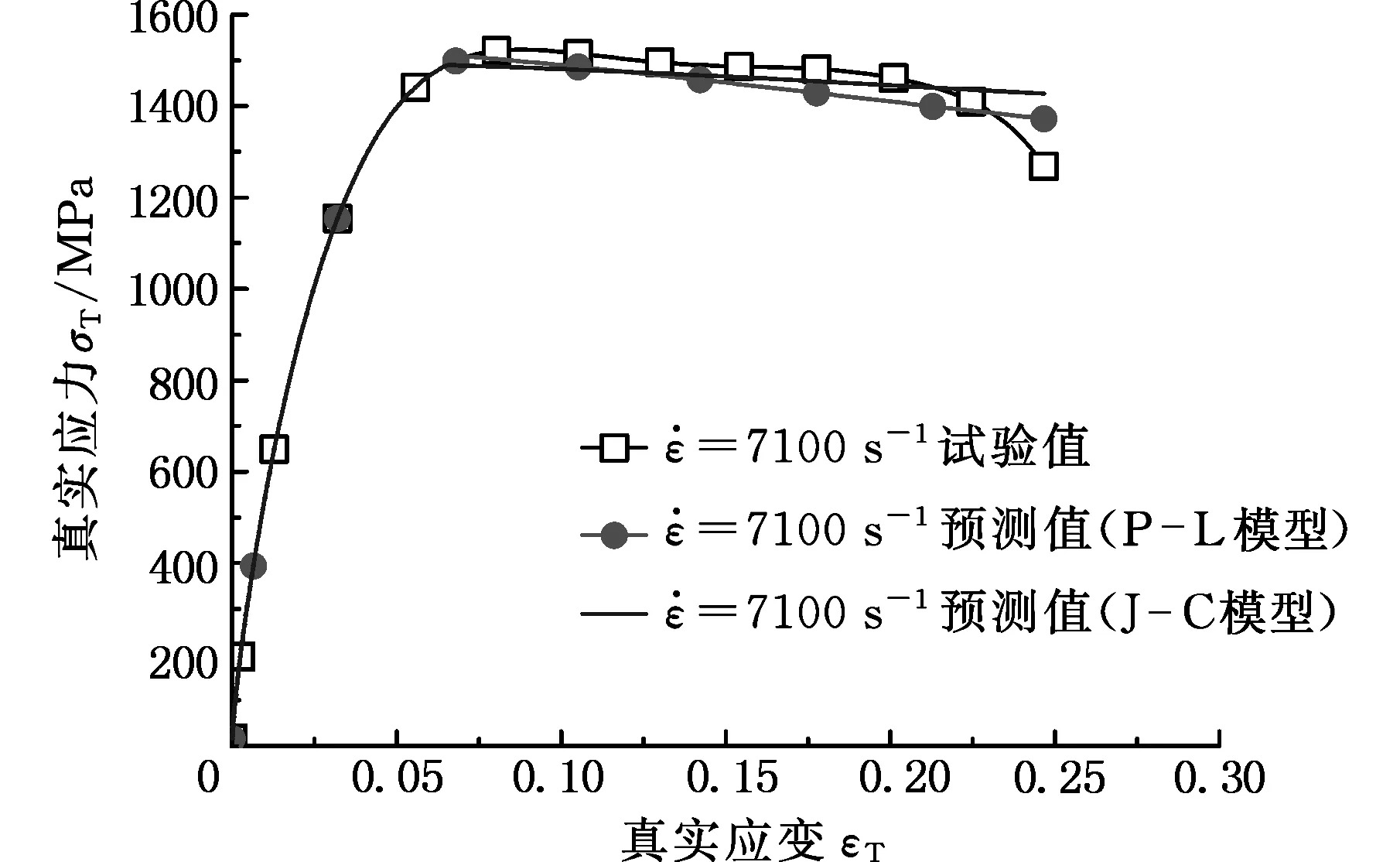
图22 模型曲线和试验结果对比 s-1)Fig.22 Comparison of model curves and test results at strain rate 7100 s-1

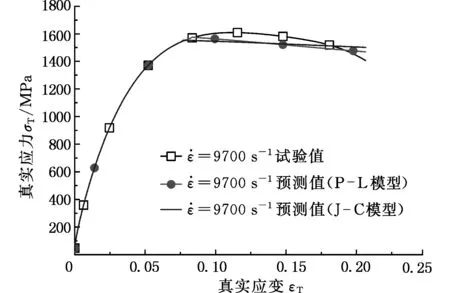
图 23 模型曲线和试验结果对比 s-1)Fig.23 Comparison of model curves and test results at strain rate 9700 s-1

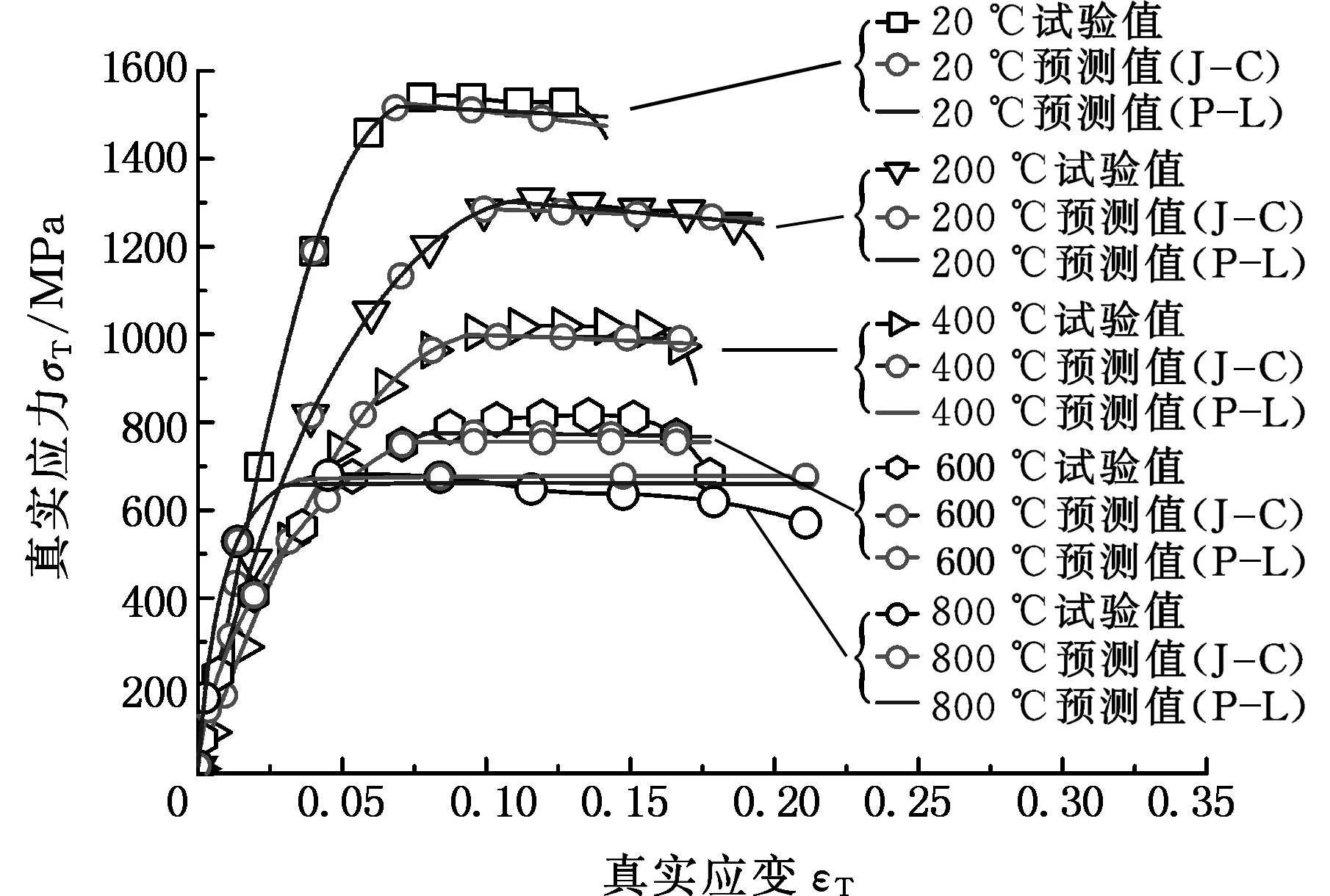
图24 应变率为5000 s-1时不同温度下应力应变曲线实测与预测结果的比较Fig.24 Comparison of model prediction with experimental results of stress-strain curves under different temperatures at strain rate 5000 s-1

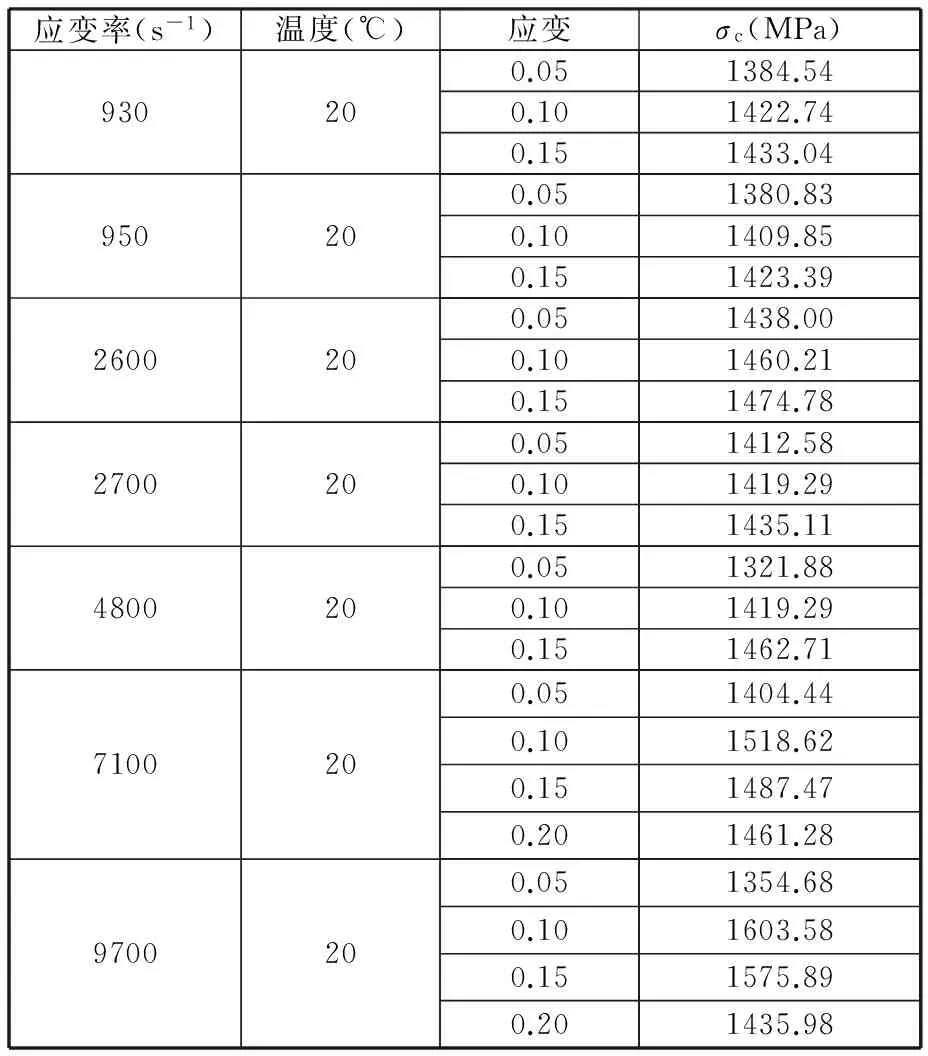
应变率(s-1)温度(℃)应变σc(MPa)930200.050.100.151384.541422.741433.04950200.050.100.151380.831409.851423.392600200.050.100.151438.001460.211474.782700200.050.100.151412.581419.291435.114800200.050.100.151321.881419.291462.717100200.050.100.150.201404.441518.621487.471461.289700200.050.100.150.201354.681603.581575.891435.98

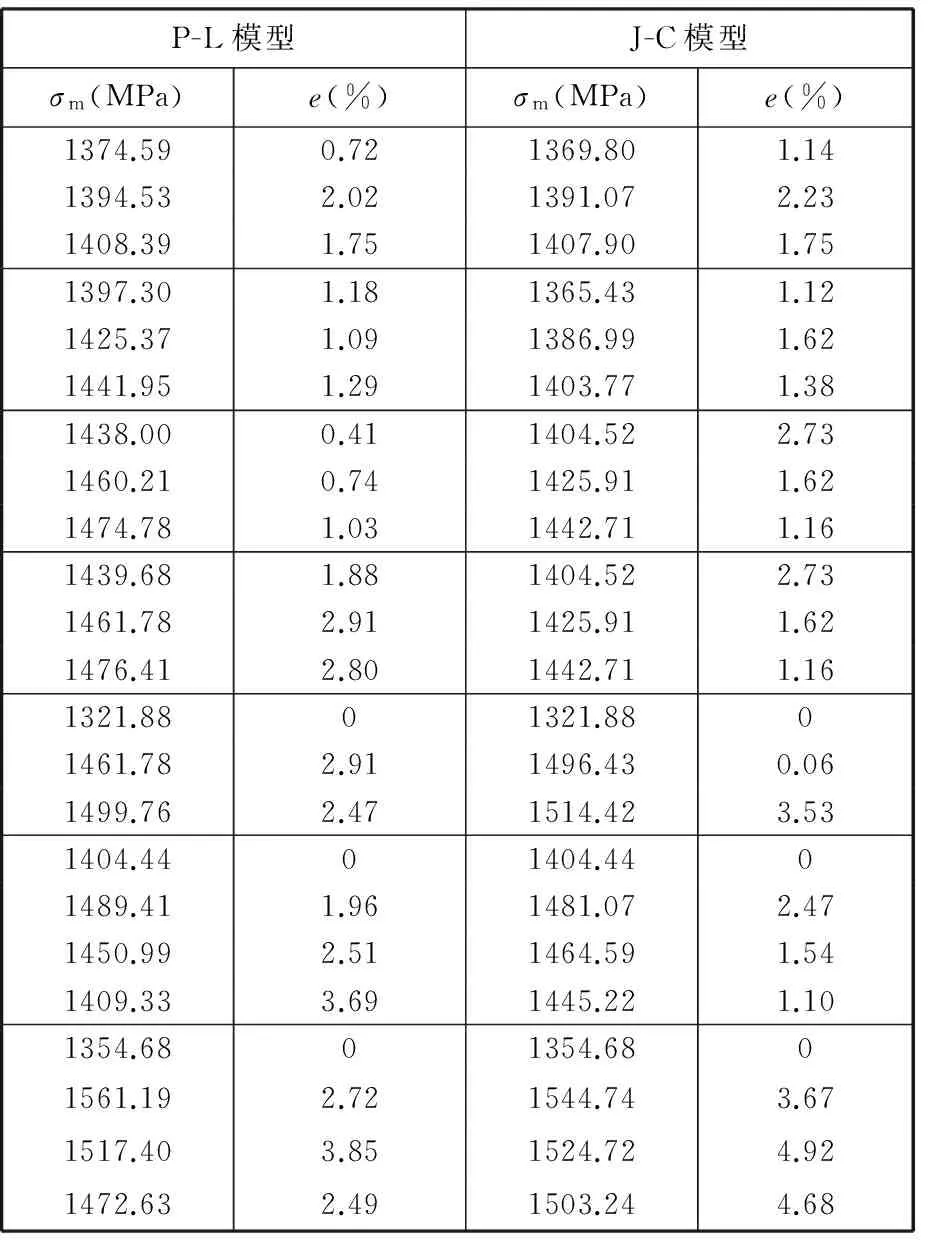
表3 本构模型预测结果的误差分析Tab.3 The constitutive model error analysis of prediction results

温度软化项。在P-L模型中第三项采用的是绝对多项式形式，而J-C模型中则采用的是相对指数形式，对于不同的材料试验曲线，既存在P-L模型优于J-C模型的情况，也存在相反情况。本次试验中P-L本构模型要略优于J-C本构模型。

3.4 P-L与J-C本构模型误差分析

本构模型预测结果的误差通过下式计算：

(28)

其中，σc和σm分别为测量曲线和预测曲线的真实应力值,e为误差。计算结果列于表2。

4 结论

(1)TC4-DT钛合金材料随着应变率的增大，真实应力增大明显，即应变率敏感性增强，而随着加热温度的升高，真实应力的下降趋势减缓，即温度敏感性减弱，此外TC4-DT在塑性变形过程中的绝热温升随着试样加热温度的升高而降低。

(2)TC4-DT钛合金材料存在临界应变率值2650 s-1， 当应变率小于2650 s-1时真实应力曲线变化较小，当大于2650 s-1时真实应力曲线发生明显变化，真实应力显著增大。

(3)本文试验对材料TC4-DT钛合金进行了Power-law和Johnson-Cook两种材料本构模型的拟合，通过对Power-Law和Johnson-Cook两种模型的拟合误差进行对比发现，两种模型的拟合误差相差不大，Power-Law模型拟合精度要略优于Johnson-Cook模型的拟合精度。

[1] 赵永庆，葛鹏. 我国自主研发钛合金现状与进展[J]. 航空材料学报, 2014,34(4): 51-61. ZHAO Yongqing,GE Peng. Current Situation and Development of New Titanium Alloys Invented in China.[J] Journal of Aeronautical Materials,2014,34(4):52-61.

[2] 于兰兰，毛小南，李辉. 温度对TC4-DT损伤容限型钛合金疲劳裂纹扩展行为的影响[J]. 稀有金属快报, 2007,26(12): 20-23. YU Lanlan, MAO Xiiaonan, LI Hui. Effects of Temperature on Fatigue Crack Growth Behavior of TC4-DT Damage Tolerance Titanium Alloy[J]. Rare Metals Letters, 2007, 26(12): 20-23.

[3] 刘清风，程鑫，王宁昌，等. 动态冲击载荷下无氧铜的力学性能研究[J]. 机械强度, 2015,180(4): 607-612. LIU Qingfeng,CHENG Xin,WANG Ningchang, et al. Dynamic Mechanical Properties of Oxygen Free Copper Under the Impact Load[J]. Journal of Mechanical Strength,2015,180(4):607-612

[4] 郭伟国. 一种新型奥氏体不锈钢的塑性流变行为研究[J]. 西北工业大学学报, 2001,19(3): 476-479. GUO Weiguo. PlasticFlow Behavior of a New Austenitic Stainless Steel AL6-XN under Different Strain Rates and Temperatures[J]. Journal of Northwestern Poly Technical University,2001,19(3):476-479

[5] 孔金星，陈辉，何宁，等. 纯铁材料动态力学性能测试及本构模型[J]. 航空学报,2014,34(7):2063-2071. KONG Jinxing,CHEN Hui,HE Ning,et al.Dynamic Mechanial Property Tests and Constitutive Model of Pure Iron Material[J]. Acta Aeronautica et Astronautica Sinica,2014,35(07):2064-2065.

[6] Wang Y L, Hui S X, Liu R, et al. Dynamic Response and Plastic Deformation Behavior of Ti-5Al-2.5Sn ELI and Ti-8Al-1Mo-1V Alloys Under High-strain Rate[J]. Rare Metals,2014,33(2):127-133.

[7] 张长清，谢兰生，陈明和，等. 高应变率下TC4-DT钛合金的动态力学性能及塑性本构关系[J]. 中国有色金属学报, 2015,25(2):323-329. ZHANG Changqing,XIE Lansheng,CHEN Minghe,et al. Dynamic Mechanical Property and Plastic Constitutive Relation of TC4-DT Ti Alloy under High Strain Rate[J]. The Chinese Journal of Nonferrous Metals,2015,25(2):323-329

[8] LIU J, ZENG W, ZHU Y, et al. Hot Deformation Behavior and Flow Stress Prediction of TC4-DT Alloy in Single-phase Region and Dual-phase Regions[J]. Journal of Materials Engineering and Performance,2015,24(5):2140-2150.

[9] 张正礼. 几种铝合金材料动态力学性能测试[J]. 中国民航大学学报,2014,32(1):41-45. ZHANG Zhengli. Testing of Dynamic Mechanical Property of Several Aluminum Alloy Materials[J].Journal of Civil Aviation University of China,2014,32(1):41-45.

[10] DAVIES E D, HUNTER S C. The Dynamic Compression Testing of Solids by the Method of the Split Hopkinson Pressure Bar[J]. Journal of the Mechanics and Physics of Solids,1963,11:155-179

[11] 王晓燕，卢芳云，林玉亮. SHPB实验中端面摩擦效应研究[J]. 爆炸与冲击, 2006,26(2):134-139. WANG Xiaoyan, LU Fangyun , LIN Yuliang, Study on Interfacial Friction Effect in The SHPB Tests[J]. Explosion and Shock Waves,2006,26(2):134-139.

[12] CHEN W, SONG B. Split Hopkinson (Kolsky) Bar[M]. NewYork: Springer US,2011.

[13] NEMAT-NASSER S, LI Y F, ISAACS J B. Experiments Computational Evaluation of Flow Stress at High Strain Rates with Application to Adiabatic Shear Banding[J].Mechanics of Materials,1994,17(2):111-134

[14] ARMSTONG R W, WALLEY S M. High Strain Rate Properties of Metals and Alloys[J]. International Materials Reviews,2008,53(3):105-129

[15] 李玉龙，索涛，郭伟国，等. 确定材料在高温高应变率下动态性能的Hopkinson杆系统[J]. 爆炸与冲击,2005,25(6):487-492. LI Yulong, SUO Tao, GUO Weiguo, et al. Determination of Dynamic Behavior of Materials at Elevated Temperatures and High Strain Rates Using Hopkinson Bar[J]. Explosion and Shock Waves,2005,25(6):134-139.

[16] 郭伟国. 高温分离式Hopkinson压杆技术及其应用[J]. 实验力学, 2006,21(4):447-453. GUO Weiguo, The Split Hopkinson Pressure Bar Technique of High Temperatures and Its Application[J].Journal of Experimental Mechanics,2016,21(4):134-139

[17] 罗皎，李淼泉，李宏，等. TC4钛合金高温变形行为及其真实应力模型[J]. 中国有色金属学报,2008,18(8):1395-1401. LUO Jiao, LI Miaoquan, LI Hong, et al, High Temperature Deformation Behavior of TC4 Titanium Alloy and Its Flows Stress Model[J]. The Chinese Journal of Nonferrous Metals,2008,18(8):1395-1401.

[18] 黄志斌，万敏，伍惠，等. TC4钛合金神经网络本构模型及在有限元模拟中应用[J]. 塑性工程学报,2013,20(1):89-94. HUANG Zhibin,WAN Min, WU Hui, et al, Constitutive Model of Ti-6Al-4V-Alloy Based on Artificial Neural Network and Its Application on FEM Simulation[J]. Journal of Plasticity Engineering,2013,20(1):89-94.

[19] 鲍俊瑶，徐超. TC11钛合金高温塑性本构方程研究[J]. 安徽建筑工业学院学报,1999,7(4):43-47. BAO Junyao,XU Chao. Research on Constitutive Equations for Hot Working of Metals[J].Journal of Anhui Institute of Architecture,1999,7(4):43-47

[20] PROULX T, TAMAOGI T, SOGABE Y. Examination of Validity for Viscoelastic Split Hopkinson Pressure Bar Method[M]. NewYork: Springer US,2011:77-83.

[22] SAWAS O, BRAR N S, BROCKMAN R A. Dynamic Characterization of Compliant Materials Using an Al-polymeric Split Hopkinson Bar[J]. Experimental Mechanics,1998,38(3):204-210.

[23] CHEN W, LU F, ZHOU B. A Quartz-crystal-embedded Split Hopkinson Pressure Bar for Soft Materials[J]. Experimental Mechanics,2000,40(1):1-6.

(编辑 王艳丽)

Dynamic Mechanics Behavior and Constitutive Model of TC4-DT Titanium Alloy Materials

AI Jianguang1JIANG Feng1YAN Lan2

1.Institute of Manufacturing Engineering,Huaqiao University, Xiamen，Fujian,361021 2.College of Mechanical Engineering and Automation,Huaqiao University, Xiamen，Fujian， 361021

The dynamic mechanics behavior experiments of TC4-DT titanium alloy materials were carried out using high temperature Hopkinson bar with synchro assembly system SHPB apparatus under different strain rates (930～9700 s-1) and at room temperature and under different temperature (20～800 ℃) at high strain rate(5000 s-1)respectively.The stress-strain curves of TC4-DT titanium materials were obtained at high temperatures and high strain rates. The TC4-DT materials have the strain rate plasticity effect and have the critical strain rate value, above this value, the strain rate sensitivity increases obviously. The softening effect is weakened with the increase of heating temperature of the materials. The experimental data were fitted Power-Law and Johnson-Cook two kinds of thermal visco-plastic constitutive equation respectively; and the two kinds of dynamic constitutive model parameters were obtained. the two kinds of fitting curves and the experimental data obtained were compared and analyzed. The results show that the two model predictions have a good agreement with the experimental data. Futher,the fitting precision of the two curves were compared and results show that the fitting errors of the two models are not very different, but the precision of the Power-Law model is slightly better than that of Johnson-Cook model.

TC4-DT titanium alloy; Johnson-Cook constitutive model; Power-Law constitutive mode; strain rate; split Hopkinson pressure bar(SHPB)

2016-06-06

福建省高校产学研合作科研重大项目(2014H6018)；福建省自然科学基金资助项目(2016J01237)；福建省高校杰出科研人才培养计划资助项目(JA14013)

TG115.5

10.3969/j.issn.1004-132X.2017.05.017

艾建光，男，1992年生。华侨大学制造工程研究院硕士研究生。主要研究方向为材料动态力学性能测试及表征技术。姜 峰，男，1981年生。华侨大学制造工程研究院副教授、博士。言 兰,女，1981年生。华侨大学机电及自动化学院副教授、博士。