主动控制静压轴承薄膜节流器仿真分析

黄继雄，刘 裕，李 朋

主动控制静压轴承薄膜节流器仿真分析

黄继雄，刘 裕，李 朋

(武汉理工大学 机电工程学院，武汉 430070)

介绍了一种基于超磁致伸缩薄膜控制的静压轴承节流器，即在原有薄膜节流器的基础上增加控制环节，用于实现静压轴承的主动控制。利用ANSYS进行了仿真计算，推导出了薄膜在节流器内置磁场作用下的变形规律。利用MATLAB求解雷诺方程得出油腔压力与节流间隙的数值关系，最终求出磁场强度与静压轴承油腔压力的变化关系。结果表明：超磁致伸缩薄膜控制的节流器在低磁场作用时，能够对油腔压力进行较大范围的主动调节，从而使静压轴承可以获得更高的支撑精度和刚度。

静压轴承；磁致伸缩薄膜；节流器；主动控制

0 引言

随着科学技术的发展，对机械加工精度的要求越来越高。在高精度及精密加工领域，期望静压轴承有极高的支撑精度，轴心位置不随外载荷变化，即具有无限大的刚度。另一方面，希望轴心位置能根据需要进行控制，用以实现微量进给或补偿工艺系统的变形，获得正确的切深。主动控制的静压轴承除了具有普通静压轴承的优点外，还可以通过控制薄膜的变化，对静压油腔的压力进行调节，提高静压轴承的刚度和稳定性。许多文献对静压轴承的性能进行了研究。潘云忠等[1]建立了静压轴承单自由度液压伺服控制系统的数学模型，并设计了系统硬件电路。佐晓波等[2]提出了一种新型的自补偿双锥面液体静压轴承,分析表明该轴承具有较高承载力和刚度。SangMin Lee等[3]考虑了波纹误差对静压轴承的影响，发现轴承负荷波动和承载力波是影响运行精度的重要因素。Haugaard等[4]研究了主动可倾油塾轴承的稳定性问题，以及外部控制系统对轴承稳定性造成的影响。本文在常规薄膜节流器原理的基础上，利用超磁致伸缩薄膜的伸缩特性，将节流器薄膜做成一个可控制的微型伸缩薄膜机构，在磁场作用下实现对节流器薄膜的主动控制。

1 薄膜节流器的工作原理

薄膜节流器工作原理如图1所示，从液压泵输出的压强为PS的压力油分别进入节流器的上下腔，再分别经过由薄膜上下表面与壳体圆台组成的节流间隙后流入静压油腔1和3(另外两个油腔的薄膜节流器图中未表示)。薄膜节流器的节流作用主要是靠节流间隙的变化来实现。当主轴未受到外载荷W时，由于油腔是对称分布的，若忽略主轴系统的自重，则主轴处于轴承的中心位置，节流器薄膜处于水平位置，此时，轴与轴承之间各处的间隙相同，各油腔压力(Pr)相等。当主轴受到向下的外载荷W时，主轴往油腔1的方向产生微小位移e，油腔1的压力P1增大，油腔3的压力P3减小。这时，与油腔1和油腔3相连的节流器的上下腔压力相应增大和减小，促使薄膜产生弹性变形而向上凸起，P3进一步减小，P1进一步增大，直到最终油腔1和油腔3的压力差ΔP与外载荷W平衡。在轴心同样的位移下，薄膜节流器产生的压力差ΔP比固定节流器大，相应地刚度也提高了[5]。

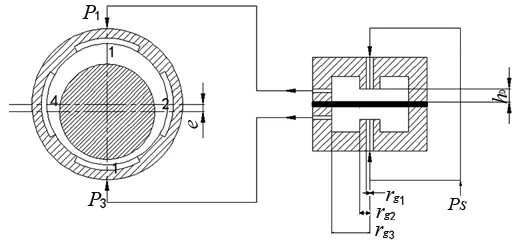
图1 薄膜节流器工作原理

2 新型薄膜节流器模型及节流原理

如图2所示，在原有薄膜节流器薄膜(衬底)俩端部的上面分别添加一层负磁致伸缩的薄膜SmFe2，在端部下面分别添加一层正磁致伸缩薄膜TbDyFe，组成衬底-薄膜的正负超磁致伸缩机构[6]。TbDyFe和SmFe2属于GMF材料，常应用于微型伸缩器的控制，TbDyFe在受到水平方向磁场作用时，薄膜在水平方向伸长，SmFe2在受到水平方向磁场作用时，薄膜在水平方向收缩，同时作用于衬底，可使其产生弯曲变形。节流器内上下腔分别布置对称的两个圆柱线圈，构成赫姆霍兹线圈[7]。赫姆霍兹线圈能在相连的两个线圈中间产生均匀分布的磁场，并且轴线中间磁场强度是叠加效果，可以产生足够的磁场强度。两组赫姆霍兹线圈分别为磁致伸缩薄膜的伸缩提供水平方向的均匀磁场。薄膜中间有一个环形的凹槽，形成岛式薄膜节流结构，使衬底在变形时中间的凸台变形几乎成水平状，用来实现均匀缝隙节流。

图2 新型薄膜节流器模型

当主轴受载荷W的作用后，沿载荷方向产生微小位移e，传感器检测出位移信号，控制系统控制线圈电流，改变磁场中的场强，使衬底端部下表面的TbDyFe薄膜伸长，使衬底端部上表面的SmFe2薄膜缩短，作用在衬底上可等效为俩个力矩，造成磁致伸缩薄膜的变形，带动衬底产生弯曲变形，改变薄膜与节流器圆台之间的节流间隙，从而改变进入静压油腔的流量，使P1增大，P3减小，托升轴颈，使主轴回到轴承中心。

3 节流器的控制模型

要对油腔压力进行精确控制，首先需要求出正负超磁致伸缩薄膜控制下的衬底中心挠度,然后求出节流间隙与油腔压力的关系，最终得到不同偏心位移时磁场强度与油腔压力的数值关系。

3.1 衬底中心挠度与磁场强度的关系

磁致伸缩薄膜采用磁控溅射工艺沉积在衬底材料上与衬底材料一起形成薄膜样品，由于薄膜在磁场中的变形受到衬底材料的约束，磁致伸缩的结果是使样品产生弯曲变形，弯曲变形量与薄膜的伸缩性能、磁场的强度、衬底的弹性性能、以及薄膜和衬底厚度等因素有关。本文主要考虑均布磁场对薄膜变形的影响。在表征薄膜磁致伸性能的指标中，线性磁致伸缩系数λ是一个重要的衡量标准。在低磁场作用下时，SmFe2和TbDyFe的磁致伸缩系数随磁场强度的变化如图3、图4所示[8-9]。

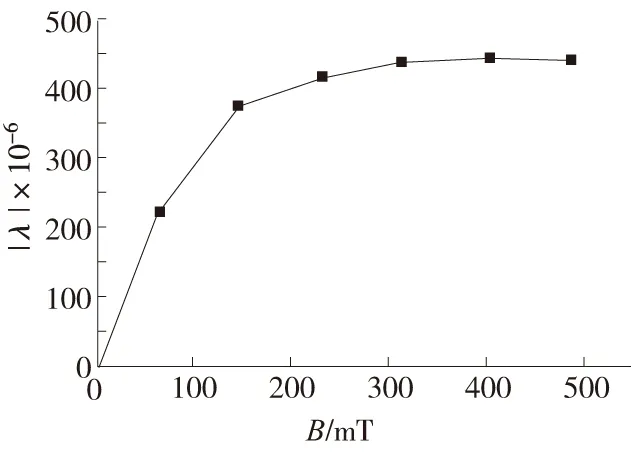
图3 SmFe2的磁致伸缩系数与磁场强度的关系

图4 TbDyFe的磁致伸缩系数与磁场强度的关系

磁致伸缩系数仅与薄膜材料有关，一般用如下公式表征其特性：

(1)

其中，dl为材料长度变化量，L为材料的长度。λ的符号为正，表明随着磁场的增强，材料的长度变化是伸长的，称为正磁致伸缩，反之，λ的符号为负，表明随着磁场的增强，材料的长度变化是缩短的，称为负磁致伸缩。

当磁致伸缩作用时，若磁致伸缩薄膜在水平方向伸长或缩短dl时，磁致伸缩线应变为dl/L，即为λ。在薄膜的弹性变形范围内，相应的磁致伸缩应力可表示为Eλ，将这一磁致伸缩力等效作用在薄膜上的体积力定义为磁致伸缩力q：

q=EλA/V

(2)

其中，A为磁致伸缩薄膜作用面积；V为薄膜体积；E为磁致伸缩薄膜的弹性模量。

在低磁场作用时，磁致伸缩薄膜有很好的灵敏度，并且磁致伸缩系数与磁场强度有近似线性关系。不同磁场对应的磁致伸缩系数λ不同，磁致伸缩力q也不同，因此可求出不同低磁场强度下的衬底变形量。由于用解析法得出衬底的变形量太过困难，因此采用有限元分析方法来求薄膜变形量与磁场强度关系，薄膜结构有限元模型如图5所示。

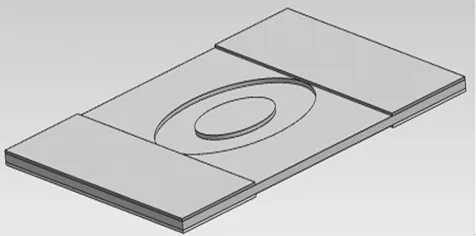
图5 薄膜伸缩机构模型

选取磁致伸缩薄膜TbDyFe和SmFe2厚度均为0.05mm，长度为33mm，宽度为9.5mm，TbDyFe的弹性模量为50GPa，SmFe2的弹性模量为140GPa，宽度为8.5mm，衬底材料为铜，长度为33mm，宽度为33mm，厚度为0.3mm，凸台直径为8mm，环槽外径为16mm。利用ANSYS软件数值求解磁致伸缩力作用下的衬底的变形量。如图6所示。

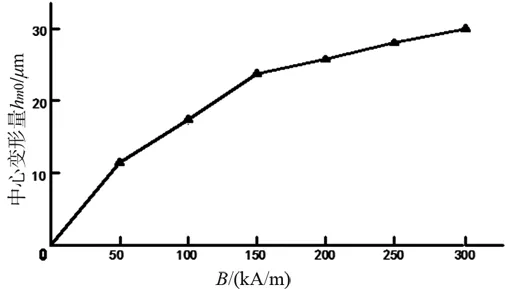
图6 衬底中心变形量与磁场强度的关系

由图6可以看出，在低频磁场(0～300kA/m)作用下，衬底弯曲变形量随着磁场强度的增大而增大，逐渐趋于饱和。变形量的变化范围在0～30μm之间，而节流间隙一般在50～80μm之间，衬底产生的位移和节流间隙是同一数量级，变形量满足薄膜变形的调节范围，因此在理论上能够实现磁场对节流间隙的调节。

3.2 节流间隙与油腔压力的关系

如图7所示，在300kA/m磁场强度作用时，衬底中间凸台的变形位移相同，满足岛式薄膜均匀间隙节流的特点。由于新型的薄膜节流器与普通薄膜节流器都是通过节流间隙节流，因此流量公式是一样的[10]。如式(3):

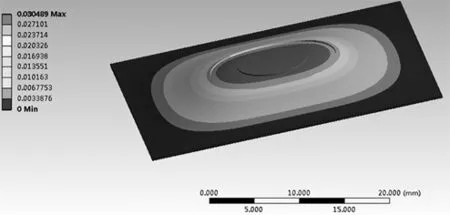
图7 衬底变形位移图

(3)

式中，rc1为薄膜节流器进油孔半径(m)；rc2为薄膜节流器圆台直径(m)；h0为圆台与薄膜之间的初始间隙(m)；μm为薄膜平均变形量(m)。

静压油腔的压力求解通常使用雷诺方程来求解，而雷诺方程的解析很难求出，因此采用数值解雷诺方程，一般使用有限元差分法求解，使用计算机软件MATLAB编制程序来完成数值计算。雷诺方程如式(4)：

(4)

式中，U为轴旋转线速度大小，不包括方向；η为润滑油动力黏度。雷诺方程的边界条件为流量连续性方程，即薄膜节流器进入油腔的流量等于流出静压油腔的流量，它们的关系为:

Q出=Q

(5)

利用式(4)、式(5)可求得出雷诺方程解。选主轴转速n=1000r/min，主轴直径d=80mm，轴承半径间隙hc=0.025mm；节流器参数rg1=1.25mm，rg2=8mm，rg3=16.5mm，原始间隙h0=0.06mm；供油压力PS=1MPa。只考虑竖直方向的主轴的偏移，即偏位角为0，偏心率ε=e/h0取不同值时，以间隙为变量，得出上下油腔的压力差，即油膜的承载力。如图8所示。

图8 衬底中心变形量与上下油腔压力差的关系

3.3 油腔压力与磁场强度的关系

由图6和图8得到磁场与薄膜承载力的关系，如图9所示。

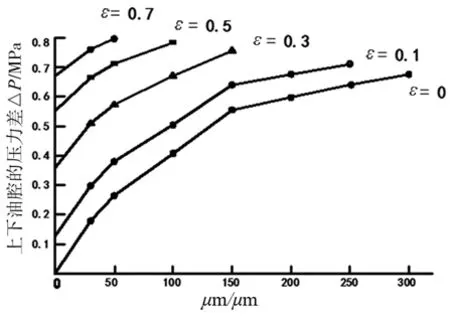
图9 磁场强度与上下油腔压力差的关系

如图9所示，在磁场强度为0～300kA/m的低磁场作用范围内，磁致伸缩薄膜节流器在主轴偏心率不同时能够实现上下油腔压力差较大范围的调节，而且成近似线性关系，选取合适油腔压力来平衡外载荷，并根据需要来使轴心的位置发生改变，以此来提高静压轴承的刚度和稳定性。

4 总结

在普通薄膜节流器的节流薄膜上添加超磁致伸缩薄膜，使薄膜节流器由自动不可控型变成主动可控型。利用有限元软件ANSYS、MATLAB等工具进行了控制关系的数值分析，得出了磁场强度与静压油腔压力的数值关系。分析表明在主轴偏移时，可通过调节线圈磁场强度对静压轴承的压力进行可控调节，进而调节轴承的动力学参数，来抑制振动和改善系统稳定性。对于主动控制静压轴承的设计有一定的指导意义，也为磁致伸缩薄膜在液压控制方面的应用提供一种新的思路。

[1] 潘云忠,刘琳霞.基于液压伺服控制的静压轴承动态特性测试[J].液压与气动,2013(4):22-24.

[2] 佐晓波,尹自强,王建敏,等.自补偿液体静压轴承静/动态特性有限元分析[J].湖南大学学报(自然科学版),2014,41(1):70-75.

[3] SangMin Lee,DeugWoo Lee,YangHyup Ha,et al.A study on the influence of waviness Error to a Hydrostatic bearing for a crankshaft Pin Turner[J],Tribology Transactions,2013,56(6):1077-1086.

[4] Haugaard A M,Santos I F.Stability of Multi Orifice Active Tilting-pad Journal Bearings[J].Tribology International,2010,43(9):1742-1750.

[5] 王仁宗.精密液体静压主轴薄膜反馈节流器结构设计及特性研究[D].郑州:中原工学院,2015.

[6] 薛光明,何忠波,李冬伟,等.超磁致伸缩材料在液压阀中的应用现状[J].液压与气动,2013(4):94-98.

[7] 郭玉川,庹晏斌,文小辉,等.改进型赫姆霍兹线圈磁场均匀性及实用性分析[J].物理实验,2015,35(11):42-46.

[8] 彭俊华,周白杨,邓光华,等.磁控溅射SmFe2GMF的工艺及膜性能研究[J].福州大学学报,2003,31(6):690-693.

[9] 万红.TbDyFe薄膜的磁致伸缩性能及其弹性、压电衬底符合效应研究[D].长沙:国防科学技术大学,2005.

[10] 李仕义.新型节流器性能研究[D].济南:山东大学,2014.

(编辑 李秀敏)

Simulation Analysis of Thin Film Restrictor of Active Control Hydrostatic Bearing

HUANG Ji-xiong，LIU Yu，LI Peng

(School of Mechanical and Electrical Engineering，Wuhan University of Technology,Wuhan 430070, China)

A giant magnetostrictive thin film restrictor of active control hydrostatic bearing was introduced in this paper, it added the control link on the base of the original thin film restrictor, and would realize the active control of hydrostatic bearing. The deformation of the thin film mechanism in the built-in magnetic field of the restrictor was deduced by the simulation calculation with ANSYS. MATLAB was used to solve the Reynolds equation, than obtained the numerical relationship between the pressure of the oil cavity and the restrictor clearance. Finally, the relationship between the magnetic field strength and the pressure of the oil chamber of the hydrostatic bearing was found. Results showed that under low magnetic field the control of giant magnetostrictive thin film restrictor could realize the active regulation of the oil cavity pressure in a large scope, so that the hydrostatic bearings could obtain higher support accuracy and stiffness.

hydrostatic bearing；giant magnetostrictive thin film；restrictor；active control

1001-2265(2017)02-0065-03

10.13462/j.cnki.mmtamt.2017.02.016

2016-06-24；

2016-07-19

黄继雄(1957—)，男，江西九江人，武汉理工大学教授，博士,研究方向为先进制造工艺及装备，(E-mail)Huangjix168@sina.com。

TH133.3;TG65

A